【PCL】sample_consensus 模块—— Random Sample Consensus model（随机样本一致性模型，RANSAC）

1、随机样本一致性模型（RANSAC）简介

在本教程中，我们将学习如何使用带有平面模型的随机样本一致性（RANSAC）来获取适合该模型的点云。

1.1理论背景

RANSAC 是“随机样本一致性”（RANdom SAmple Consensus）的缩写，它是一种迭代方法，用于从包含异常值的数据集中估计数学模型的参数。该算法由 Fischler 和 Bolles 于 1981 年提出。RANSAC 算法假设我们观察到的数据由内点和异常值组成。内点可以通过具有特定参数值的模型来解释，而异常值在任何情况下都不适合该模型。另一个必要的假设是，存在一种可以从数据中最佳估计所选模型参数的程序。

RANSAC 算法的输入是一组观测数据值、一个可以解释或拟合观测值的参数化模型以及一些置信参数。

RANSAC 通过迭代选择原始数据的随机子集来实现其目标。这些数据是假设的内点，然后通过以下步骤测试该假设：

1. 将模型拟合到假设的内点，即从内点重建模型的所有自由参数。
2. 然后，所有其他数据都针对拟合模型进行测试，如果某个点与估计模型拟合良好，则也将其视为假设的内点。
3. 如果足够多的点被分类为假设的内点，则估计的模型是合理的。
4. 从所有假设的内点重新估计模型，因为它仅从初始的假设内点集中估计。
5. 最后，通过估计内点相对于模型的误差来评估模型。

此过程重复固定次数，每次生成一个由于分类为内点的点太少而被拒绝的模型，或者生成一个带有相应误差度量的改进模型。在后一种情况下，如果其误差低于上次保存的模型，则保留改进的模型。

RANSAC 的一个优点是它能够对模型参数进行鲁棒估计，即即使数据集中存在大量异常值，它也可以高精度地估计参数。RANSAC 的一个缺点是计算这些参数所需的时间没有上限。当计算的迭代次数有限时，获得的解决方案可能不是最优的，甚至可能不是一个很好地拟合数据的解决方案。通过这种方式，RANSAC 提供了一种权衡；通过计算更多的迭代次数，生成合理模型的概率会增加。RANSAC 的另一个缺点是它需要设置特定问题的阈值。

RANSAC 只能估计一个特定数据集的一个模型。对于任何单一模型方法，当存在两个（或更多）模型时，RANSAC 可能无法找到任何一个。

1.2图像示例

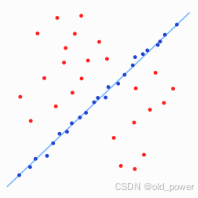
左侧和右侧的图像展示了 RANSAC 算法在二维数据集上的简单应用。左侧的图像是包含内点和异常值的数据集的视觉表示。右侧的图像以红色显示所有异常值，并以蓝色显示内点。蓝线是 RANSAC 工作的结果。在这种情况下，我们试图拟合数据的模型是一条线，看起来它非常适合我们的数据。

2、代码实现

2.1 RandomSampleConsensusModel.cpp

#include <iostream>
#include <thread>

#include <pcl/console/parse.h>
#include <pcl/point_cloud.h> // for PointCloud
#include <pcl/common/io.h> // for copyPointCloud
#include <pcl/point_types.h>
#include <pcl/sample_consensus/ransac.h>
#include <pcl/sample_consensus/sac_model_plane.h>
#include <pcl/sample_consensus/sac_model_sphere.h>
#include <pcl/visualization/pcl_visualizer.h>

using namespace std::chrono_literals;

pcl::visualization::PCLVisualizer::Ptr
simpleVis (pcl::PointCloud<pcl::PointXYZ>::ConstPtr cloud)
{
   
  // --------------------------------------------
  // -----Open 3D viewer and add point cloud-----
  // --------------------------------------------
  pcl::visualization::PCLVisualizer::Ptr viewer (new pcl::visualization::PCLVisualizer ("3D Viewer"));
  viewer->setBackgroundColor (0, 0, 0);
  viewer->addPointCloud<pcl::PointXYZ> (cloud, "sample cloud");
  viewer->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3, "sample cloud");
  //viewer->addCoordinateSystem (1.0, "global");
  viewer->initCameraParameters ();
  return (viewer);
}

int
main(int argc, char** argv)
{
   
  // initialize PointClouds
  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
  pcl::PointCloud<pcl::PointXYZ>::Ptr final (new pcl::PointCloud<pcl::PointXYZ>);

  // populate our PointCloud with points
  cloud->width    = 500;
  cloud->height   = 1;
  cloud->is_dense = false;
  cloud->points.resize (cloud->width * cloud->height);
  for (pcl::index_t i = 0; i < static_cast<pcl::index_t>(cloud->size ()); ++i)
  {
   
    if (pcl::console::find_argument (argc, argv, "-s") >= 0 || pcl::console::find_argument (argc, argv, "-sf") >= 0