PID温度控制

PID中P的作用

本人花了两千多在正点原子学的PID，本着学术无边界的原则分享出来，另外模糊以及自整定后续整理中

假设设定温度为 60℃，然后使用一个固定占空比的 PWM 信号去加热加热块，要想让加热块的温度能够固定在 60℃是非常困难的。有效时间短，加热抵不住散热，这样温度到不了 60℃，加热超过散热，温度又会一直上升，超过 60℃。

那有没有办法让温度固定在 60°呢？有的。那就是测量温度距离目标温度比较远的时候全速加热，在接近目标温度时，降低 PWM 占空比(当然，这个有效时间增加的热量要超过散掉的热量)，超过目标温度后不再加热。具体实现时，我们可以这样操作：

1.温度小于目标温度时，我们让 PWM 的有效加热时间与目标温度-测量温度的差值正相关。
也即两者具有以下关系:

out = Kp * (Sv - Pv) （1）

其中，out 代表有效加热时间。 也就是PWM的占空比。
Kp 是比例系数，Sv 代表目标温度，Pv 代表测量温度。
比如，我们设定 Kp =20,Sv = 60, PWM 的周期为 500ms(对应的计数器次数为 1000 次)则

①当 Pv = 30 时， out = 20 * (60 - 30) = 600，此时一个 PWM 周期内有 60%的时间是有效加热时间。
②当 Pv = 40 时，out = 20 * (60 - 40) = 400,此时一个 PWM 周期内有 40%的时间是有效加热时间。
③当 Pv = 50 时，out = 20*(60 - 50) = 200，此时一个 PWM 周期内有 20%的时间是有效加热时间。

可以看到，随着加热时温度的增加，目标温度和测量温度的差值变小，造成每个 PWM的有效加热时间逐渐减小，这样升温慢慢变慢，温度就可以稳定 在 60°了。

在上面的讨论中，我们还看到，如果目标温度比测量温度大太多，比如目标温度-测量温度 = 55°，则此时 out 的值超过 1000。由于一个计数周期最多 1000，所以此时最多取 1000的值装入 TIM->CCRx 即可。

2.测量温度大于目标温度。此时应该将 PWM 的有效加热时间设置为 0，停止加热。
下面我们来看这样一个实验。实验参数为:

PWM 周期为 500ms，目标温度 = 60°(当前环境温度约为 18°C)。为了增加测量精度，

我们将温度值增加 10 倍来考虑，相应的，Kp 的值要减小 10 倍。现在我们取 Kp = 2。
以下是实验结果。

实验 2 Kp = 2

由上图可以看到，稳定后，实际温度在目标温度附近震荡。为了方便观看 Kp 的作用，我们给出了不同 Kp 时的实验结果图

实验 2 Kp = 1

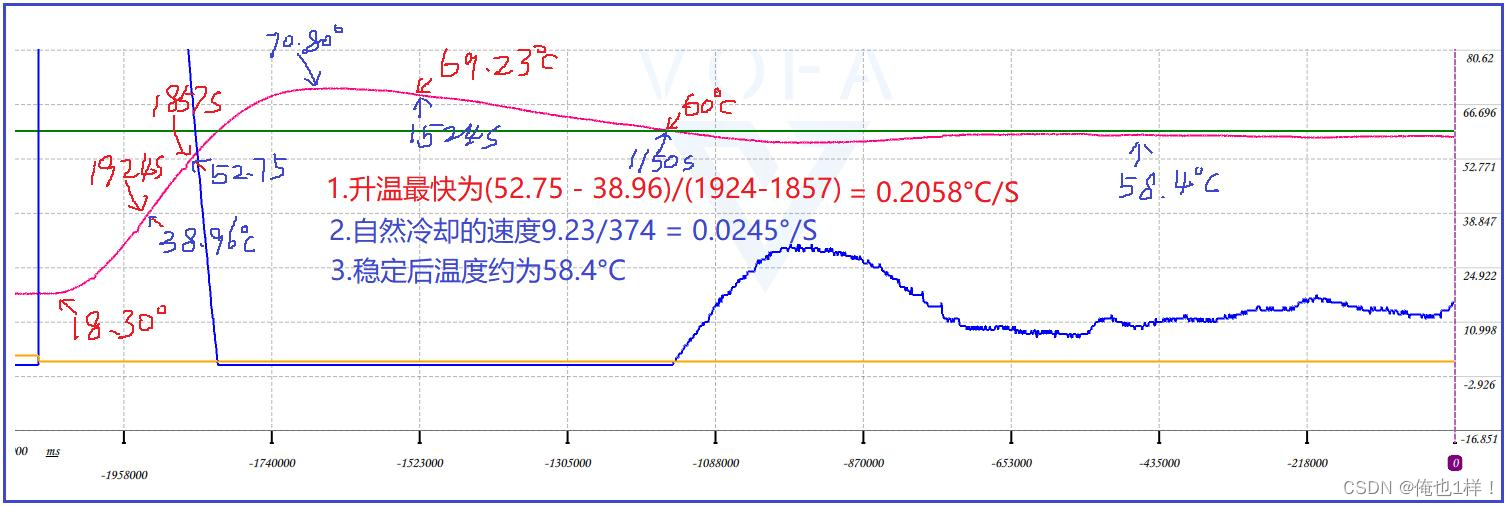
实验 3 Kp = 5

超调严重

实验 4 Kp = 0.5

超调少，但是稳定后没有到达目标位置。

实验 5 Kp = 0.8

可以看到，稳定后的温度在 58.7°C 附近。

可以看到，Kp 的值比较小时，加热不足以抵掉散热，所以稳定后的温度比目标温度小。而在 Kp 较大时，由于 P 的调节作用比较迟，加热时间相对较长，而温度具有很大的滞后性，停止加热后温度会继续飙升，所以会有超调现象(实际温度超过目标温度)，而且 Kp 的值越大，超调就越严重。

1.2 Kp 的选择

在实际的温度控制中，我们可能直接使用目标温度-测量温度来计算输出，也有可能增加 10 倍或者 100 倍来计算输出。那此时比例系数 Kp 的值如何取呢？
这个要看你想在测量温度达到什么温度时使能比例控制而定。下面我们举常见的 2 种情况来说明。
1.将目标温度和测量温度放大 10 倍来考虑。
①你想在距离目标温度有30°时使能比例控制。距离目标温度为30°才控制，意味着(Sv- 30°)是一个临界点，在这个临界点，out 刚好等于 1000—即还在全速加热。而当测量温度超过这个距离后，out 就小于 1000 了，它的值将随着温度的升高越来越小。所以，在临界点有:

out = Kp * (Sv10 - Kv10) -> 1000 = Kp * (Sv10 - (Sv * 10 - 3010 )) -> Kp = 3.33

②你想在距离目标温度有40°时使能比例控制。距离目标温度为40°才控制，意味着(Sv-40°)是一个临界点，在这个临界点，out 刚好等于 1000—即还在全速加热。而当测量温度超过这个距离后，out 就小于 1000 了，它的值将随着温度的升高越来越小。所以，在临界点有:

out = Kp * (Sv10 - Kv10) -> 1000 = Kp * (Sv10 - (Sv * 10 - 4010 )) -> Kp = 2.5

其它同理。
2.将目标温度和测量温度放大 100 倍来考虑。
①你想在距离目标温度有30°时使能比例控制。距离目标温度为30°才控制，意味着(Sv- 30°)是一个临界点，在这个临界点，out 刚好等于 1000—即还在全速加热。而当测量温度超过这个距离后，out 就小于 1000 了，它的值将随着温度的升高越来越小。所以，在临界点有:

out = Kp * (Sv100 - Kv100) -> 1000 = Kp * (Sv100 - (Sv * 100- 30100 )) -> Kp = 0.333

②你想在距离目标温度有40°时使能比例控制。距离目标温度为40°才控制，意味着(Sv-40°)是一个临界点，在这个临界点，out 刚好等于 1000—即还在全速加热。而当测量温度超过这个距离后，out 就小于 1000 了，它的值将随着温度的升高越来越小。所以，在临界点有:

out = Kp * (Sv100 - Kv100)->1000 = Kp * (Sv100 - (Sv * 100 - 40100 )) -> Kp = 0.25

其它同理。

由于温度具有很大的滞后性，所以距离目标温度为 40°的点是一个关键点，我们可以先在这个点计算出 Kp 的值代入 PID 的公式去计算 PID 的输出，并观察结果，然后再根据具体结果来调节 Kp。

PID中I( 积分项) 的作用

在前面的比例项输出实验中，当 Kp = 0.8 时可以看到，稳定后的温度在 58.7°C 附近，没有达到目标温度 60°，此时出现的这种
差值我们叫稳态误差。那有没有一种办法能够让它稳定后达到 60°呢？有，
就是将误差的积累转为输出，叠加到比例项上，一起参与对 PWM 的有效时间进行控制。

我们举一个简单的例子来说明。假设稳定后的温度为 58°，比目标温度少 2°。我们将这个 2°进行累加，每 500ms 累加一次，
则有 2+2+2+2+…,该累加项叠加到比例项，
使得输出为

out = Kp*2+ Ki *(2+ 2 + 2 +…) (1)

式(1)中，Ki 为积分系数。
由式(1)可以看到，当误差积累到一定程度后，out 将会是一个比较大的值，有效加热时间增加，温度会重新慢慢提升，并到达 60°C 处。
而当温度超过 60°后，由于设定值-测量值为负，所以比例项和积分项都为负，out 的输出为 0，系统不对加热块进行加热，加热块温度下降。这样反复加热散热，最终使得温度被稳定在目标温度处。
我们将这种差值进行累加并和比例项一起影响输出 PID 算法的输出 out，可以使得系统能够比较好地稳定于目标温度处。这种累加就是数学上的积分，将该积分离散后叠加上比例项的结果如式(2)所示。

out = Kp*E(k)+ Ki *(E(k=1) + E(k = 2) + E(k = 3) +…) (2)

其中，E(k)为目标值 - 第 k 次的测量值。
下面我们设置 Ki = 0.004,Kp 仍然取 0.8，然后看一下实验结果。

由图可以看到，增加积分项后，稳态误差被消除了。但是，由于整个过程都使用了积分，所以导致超调严重，而且振荡 1 个多小时才达到稳定。所以在使用积分的时候一定要注意，一定要根据具体的情况来使用积分项。比如先使用 Kp 调整使得稳态误差比较小，然后再根据稳态误差来确定何时使用积分。

下面我们再来看一个实验，就是在目标温度 - 测量温度在±5°时才使用积分的情况，
结果如图所示。

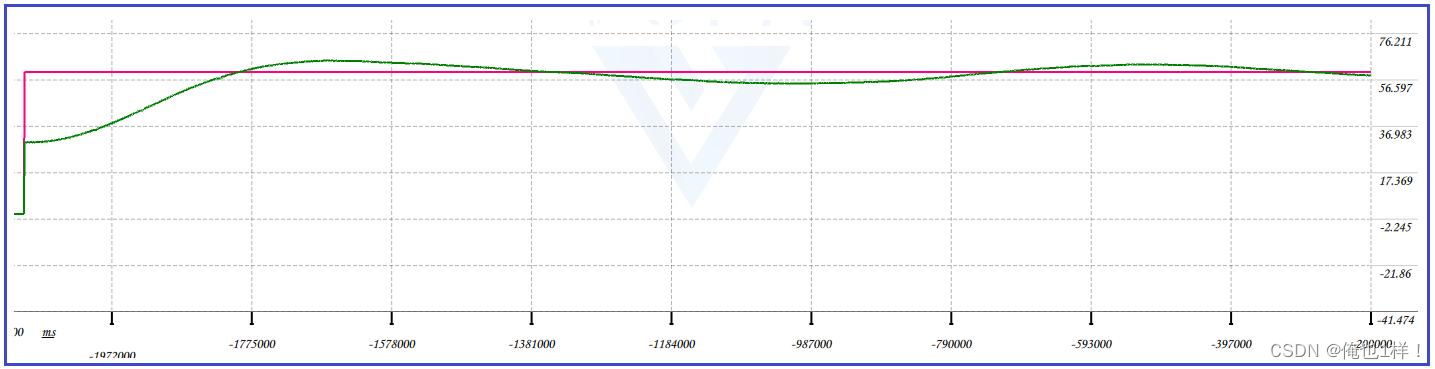
可以看到，使用积分限制后，超调大大减小，到达稳定的时间也大大缩短。

PID 中 D (微分项) 作用

在前面的学习中，我们知道了如果 Kp 比较大，则由于 PWM 调制点比较迟，导致加热时间比较久，进而产生较大的超调。而在很多工业设备中，过高的温度是不允许的。比如一些纸浆机，过高的温度会导致设备/模具损坏，所以超调的抑制非常重要。那怎么样才能抑制超调呢？
我们来分析一下加热棒被加热时的特点。

1.当测量温度小于目标温度时，无论是比例项还是积分项，它们对有效加热时间的贡献都是正的，所以叠加后会延长整体的加热时间并进而导致温升过快–当然，我们考虑的是加热大于散热的情况。

2.当测量温度大于目标温度时。比例项和积分项都是负的，对有效加热时间的贡献是负的。由加热棒的加热特点可知，我们需要对测量温度小于目标温度时的情况进行重点关注。当测量温度小于目标温度时，我们需要在 PID 的输出中增加一个对温度增加敏感的项，温度增加快，它的值就大，温度增加小，它的值就小，而且它起的作用和比例项、积分项的作用相反，也就是说它对有效加热时间的贡献是负的。那该选项应该是怎么样的呢？下面我们结合图来分析。

图中为单纯比例项作用时的情况。由图可见

①当时间从 1 增加到 2 时，温度增加 4°。
②当时间从 2 增加到 3 时，温度增加 8°。
③当时间从 3 增加到 4 时，温度增加 10°。

可以看到时间从 1 到 4 时，温度增加越来越快，所以抑制项也要越来越强，也就是说新增加的抑制项应该与温度的变化率成正比，

即具有如下关系:

Dout = Kd’ * ΔEk/Δt (1)

其中，Dout 为抑制项的输出，Kd’为比例系数，ΔEk = lastPv - Pv 为前后相邻两次测量出的温度的差(温度的变化)，Δt 为前后两次测量的时间差。lastPv 为上一次测量出的温度，Pv为当前测量出来的温度。
因为

ΔEk = lastPv - Pv (2)
=( Sv - Pv) - (Sv - lastPv)

其中 Sv-Pv 为当前测量温度和目标温度之差。Sv - lastPv 为上一次的测量温度和目标温度之差。所以ΔEk 又可以写成

ΔEk =lastEk -Ek (3)

该公式就是当前各大教材、各大网站给出的温差变化的公式。不过在本教程中，我们直接使用公式(2)而不是公式(3)。
下面我们回到式(1)继续讨论，如下：

①从 t = 1 到 t = 2 时，Dout = Kd’ * (32 - 34) /1 = Kd’*(-2);
②从 t = 2 到 t=3 时，Dout = Kd’ * (34 - 42)/1 = Kd’ * (-8);

由于通常情况下 Kd’都是正直，所以升温时 Dout 的结果是一个负值。
实际上，式(1)可以做如下变化

Dout = Kd’ * ΔEk/Δt = Kd’ * dEk/dt (4))

由(4)式可以看到，这是一个微分方程，用于描述 Dout 变化趋势，所以 Dout 实际上就是微分项的输出，而 Kd’为微分系数。
加入微分项后，PID 的输出变为了式(5)的样子：

out = Kp * Ek + Ki * SEk + Kd *ΔEk (5))

其中，Kd = Kd’/dt 为重新定义后的微分系数。由于微分项和温度的变化率相关，所以它只能阻碍而不能阻止温度的变化。
下面我们假设 Kd = 300，然后来看一下微分项的抑制效果。其中 Kp = 2, Ki = 0，先去掉积分效果。
先来看没有微分项时的结果，如图所示。

下面是增加微分项后的结果。

由图可以看到，增加微分项后，能够有效抑制超调。但是在温度反转的时候由于微分项会非常大，所以反转非常困难，这时候就需要积分项的累积去抵消掉这个大的反转，使得温度能够回到目标位置。如果没有积分项，结果很可能是曲线一直发散。

“如果你不去追逐自己的梦想，有一天你会被雇来帮助别人实现他们的梦想。” - 扖夫·乔布斯（Steve Jobs）