opencv学习 边缘检测 --拉普拉斯算子（Laplace）

摘要

　　Laplace算子作为边缘检测之一，和Sobel算子一样也是工程数学中常用的一种积分变换，属于空间锐化滤波操作。拉普拉斯算子（Laplace Operator）是n维欧几里德空间中的一个二阶微分算子，定义为梯度（▽f）的散度（▽·f）。拉普拉斯算子也可以推广为定义在黎曼流形上的椭圆型算子，称为拉普拉斯-贝尔特拉米算子。（百度百科）

基本理论

首先，拉普拉斯算子是最简单的各向同性微分算子，它具有旋转不变性。一个二维图像函数的拉普拉斯变换是各向同性的二阶导数，定义为：

                          

下面看三幅图：

                          图（a）                                                           图（b）                                                图（c）

图（a）为一条函数曲线， 图（b）为一阶导数，图（c）为二阶导数，可以看出二阶导数为0的点就是极值点。拉普拉斯算子就是运用这一特点作为检测图像边缘的。但是， 二阶导数的0值不仅仅出现在边缘(它们也可能出现在无意义的位置),但是我们可以过滤掉这些点。

理论解释

离散函数的导数退化成了差分，一维一阶差分公式和二阶差分公式分别为：如图2所示

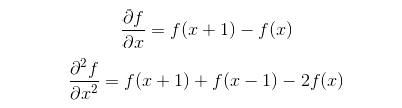
                              图2 一阶微分和二阶微分计算

解释一下，二维差分公式为什么是这样的？

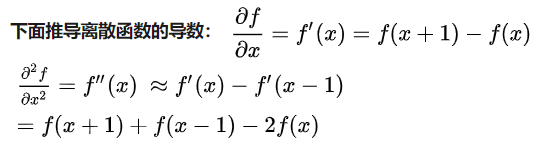
分别对Laplace算子x,y两个方向的二阶导数进行差分就得到了离散函数的Laplace算子。在一个二维函数f(x,y)中，x,y两个方向的二阶差分分别为：如图3所示

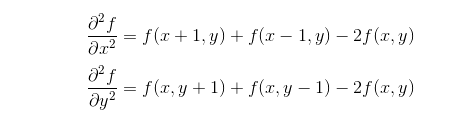
　　　　　　　图3 x,y两个方向的二阶差分

所以Laplace算子的差分形式为：

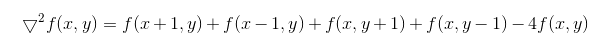
写成filter mask的形式如下：

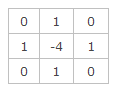
该mask的特点，mask在上下左右四个90度的方向上结果相同，也就是说在90度方向上无方向性。为了让该mask在45度的方向上也具有该性质，对该filter mask进行扩展定义为

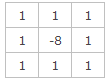
将Laplace算子写成filter mask后，其操作大同小异于其他的空间滤波操作。将filter mask在原图上逐行移动，然后mask中数值与其重合的像素相乘后求和，赋给与mask中心重合的像素，对图像的第一，和最后的行和列无法做上述操作的像素赋值零，就得到了拉普拉斯操作结果。因为Laplace算子是二阶导数操作，其在强调图像素中灰度不连续的部分的同时也不在强调灰度值连续的部分。这样会产生一个具有很明显的灰度边界，但是没有足够特征的黑色背景。背景特征可以通过原图像与Laplace算子操作后的图像混合恢复。用公式。

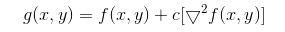
实例代码