车道调度在十字路口周围用于边缘计算驱动的自动驾驶

摘要
自动驾驶可以解放我们的双手和双脚,在日常生活中变得越来越重要。然而,车载计算和通信能力的限制阻碍了自动驾驶的快速发展。为解决这一问题,本文提出了一种名为基于边缘计算的车道调度系统(ECLSS)的新模型,用于研究在十字路口周围利用实时边缘设备对每辆车进行车道调度。在ECLSS中,十字路口周围部署了多个边缘计算设备(ECD),这些设备可通过短距离有线/无线传输从车辆和道路状况中收集信息。依托ECDs的强大计算能力和实时传输性能,我们提出了两种集中式车道管理调度方法:高效切换搜索算法(SESA)和特种车辆车道切换算法(SVLSA)。这些基于边缘计算的自动驾驶方法旨在实现车辆高速通过十字路口,并确保特种车辆能在规定时间内通过十字路口。进行了大量仿真,仿真结果表明,在典型车道切换场景中,所提出的方法相较于竞争方案具有明显优势。
1. 引言
目前,自动驾驶已成为学术界和工业界的研究热点。通过人工智能、视觉计算、雷达、监控设备和全球定位系统的协同作用,计算机能够无需人为干预地自动且安全地操控机动车。然而,自动驾驶快速发展面临的最大障碍之一是车载计算与通信能力的限制。显然,升级车载计算机并非理想方案,因为这会导致高昂的设备成本和能耗。
云计算是另一种可能的解决方案,因为它可以提供通信、计算和存储设施服务[1,2]。通过车辆和路侧单元(RSUs)的协同信息,云计算能够实现对车辆的全局调度。一些移动云计算(MCC)框架提出了利用云端服务提升移动设备性能的技术,例如CloneCloud[3],、MAUI[4]和MobiCloud[5]。此外,还提出了一种基于MCC的车辆云计算(VCC)方法,可提供直行服务质量(QoS)[6–8]。然而,云端之间的响应时间车辆和云端(响应时间以秒为单位)远大于车辆操作的对应时间(响应时间以微秒为单位),在移动云计算和车辆云计算中均无法满足自动驾驶的要求。
边缘计算作为云计算的延伸,能够在网络边缘提供实时通信性能和强大的计算能力[9,10]。由于网络带宽的发展已趋于停滞,相较于数据计算速度的发展显得滞后,传输时间开销已成为基于云端的自动驾驶技术的瓶颈。例如,波音787每秒产生5GB的数据[11],,而不久的将来一辆自动驾驶车辆每天将产生4TB的数据[12];然而,当前带宽不足以支持如此庞大的数据传输(使用20 Mbps的LTE网络上传4TB数据需要18天)。因此,为了实现更短的响应时间、更高效的处理以及减轻网络压力,数据需要在网络边缘进行处理[13]。已有若干研究基于边缘计算理念提出了针对自动驾驶的相关方案,如[14–16]。然而,这些研究存在各种局限性,例如在复杂道路条件下缺乏有效的变道方法,并且未解决特殊车辆在道路上直行的需求。此外,现有研究主要考虑直行驾驶的安全;然而,十字路口的道路状况最为复杂,在自动驾驶中需要更多关注。
本文系统地研究了在自动驾驶中利用边缘计算对十字路口周边的变道进行调度的问题,这一问题在现实生活中至关重要,但迄今为止在现有研究中尚未得到充分关注。此外,我们还考虑了特种车辆的需求,例如其通行时间。面临的挑战如下:(1)必须保证自动驾驶的安全性,尤其是变道过程中的安全性;(2)希望实现车辆快速通过十字路口的需求,特别是救护车或警车等特种车辆必须在规定时间内通过十字路口。
在本研究中,我们提出了两种十字路口周边的车道调度方法。我们的贡献如下:
1. 我们提出了一种基于边缘计算的自动驾驶新模型。由于交通状况的复杂性,该模型主要关注普通车辆和特种车辆在十字路口周围的车道调度。根据交通和车辆信息,边缘计算设备(ECD)可提供车辆车道切换的集中式调度。
2. 我们定义了安全距离以确保车辆的安全。此外,我们发现当目标车道中前方和后方均有车辆时,每次切换的额外时间开销与进行切换的车辆的位置无关。
3. 我们获得每辆车辆通过十字路口所需的时间开销范围。
4. 我们提出了两种变道算法。通过实施高效切换搜索算法(SESA),在确保所有车辆都能到达其目标方向的前提下,降低了车辆在十字路口的时间开销。对于特种车辆,我们进一步提出了特种车辆车道切换算法(SVLSA),以确保特种车辆能够在通过截止时间之前顺利通过十字路口。
我们通过大量仿真证明,所提出的调度算法和分析方法优于现有的方法。
本文的其余部分结构如下。第2节回顾了自动驾驶相关的研究。第3节介绍了系统配置,第4节给出了基于移动边缘计算(MEC)的自动驾驶问题描述。第5节提出了十字路口车道调度的调度算法。第6节通过仿真说明了所提方法的实现。结论在第7节中给出。
2. 相关工作
联网车辆的概念于1996年提出,许多研究人员一直在该领域工作,以提高驾驶的安全性和便利性[17–19]。通过允许车辆连接到互联网并与其它设备共享网络接入,提出了自动驾驶的概念。随后,许多公司、研究机构和汽车制造商对自动驾驶表现出极大兴趣[20–23]。此外,一些研究调查了在城市环境中规划与控制算法的最新进展[24–26]。然而,无线网络带宽和实时性能常常成为云计算应用于联网车辆时的性能瓶颈。
移动边缘计算(MEC)通过将处理能力从集中式云端延伸到靠近车辆的分布式边缘设备,为解决这一困境提供了方案。为了满足通信与计算两方面的需求,侯学仕等人在[14]中提出了车辆作为基础设施支持通信与计算的综述。结合云端和MEC的特点,佐佐木健吾等人提出了一种基于基础设施的车辆控制系统,该系统在边缘服务器与云端服务器之间共享内部状态,并实现动态

根据网络状况分配计算资源,并对收集的传感器数据进行必要的计算切换,以实现安全驾驶[29]。施卫松等人在基于移动边缘计算的自动驾驶系统设计方面开展了大量工作,他们提出了为网联自动驾驶车辆构建开放车载数据分析平台(OpenVDAP)以及最优的工作负载卸载与调度策略[30]。此外,基于OpenVDAP,他们提出了CAVBench,这是首个面向网联自动驾驶车辆场景中边缘计算系统的基准测试套件,包含六个典型应用,覆盖四种主流的网联自动驾驶车辆场景,并采用四个数据集作为标准输入[31]。此外,在[32]中提出了一种模块化方案,这是一种集成化的自动驾驶教学方法。
十字路口的交通状况最为复杂,然而现有的研究工作均未关注这一问题。此外,特种车辆的通行时间也是一个关键问题。因此,迫切需要研究车道调度方法,以确保不同类型的车辆能够安全、快速地通过十字路口。
3. 系统配置
在本节中,我们提出了一种新颖的自动驾驶系统,称为基于边缘计算的车道调度系统(ECLSS),以确保车辆能够安全且快速地通过十字路口。ECLSS包含三个层级。
- 底层由车辆构成。它们可以与部署在道路上的边缘计算设备(ECD)进行无线交互。
- 中间层由ECDs构成。它们可以与车辆(通过无线方式)以及云端(通过有线方式)进行信息交互。此外,对具有实时性要求的车辆请求,也在ECD中执行。
- 顶层是云端,它可以通过ECD向车辆提供长距离路径规划和大量交通信息。
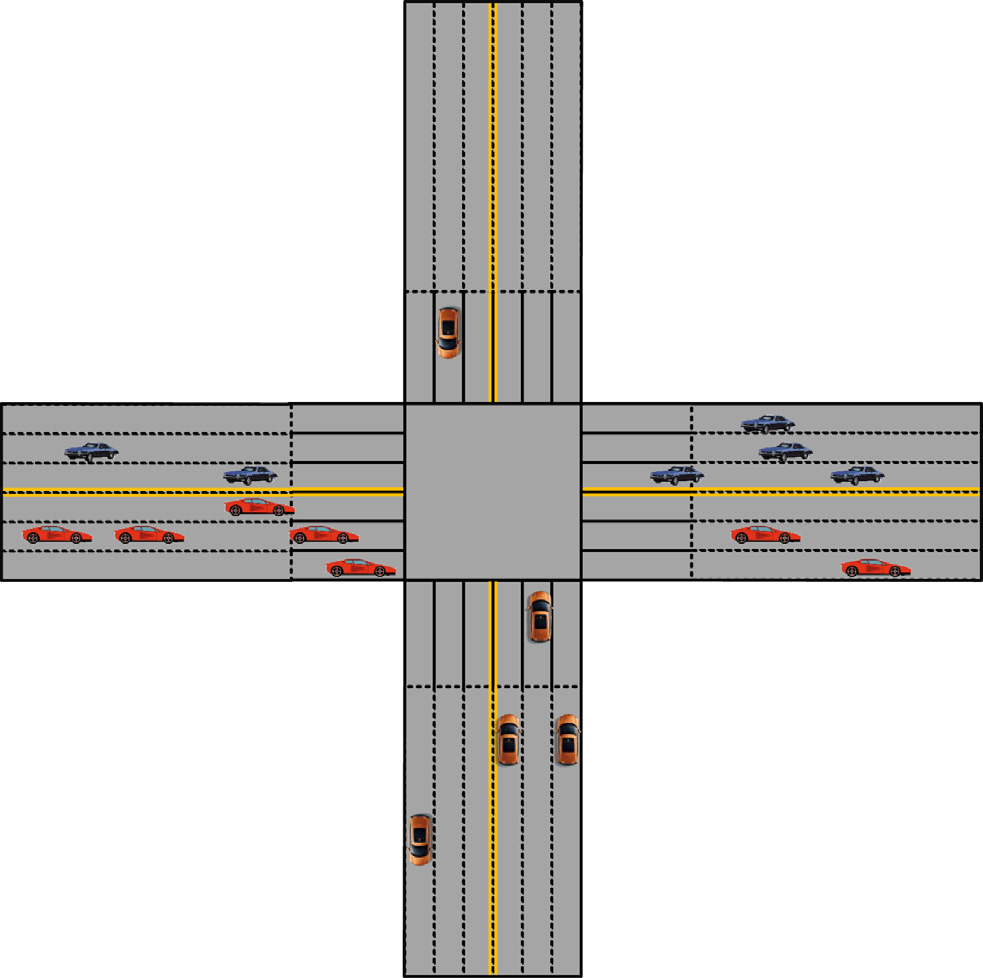
如图1所示,交通岗亭周围有四个ECD和多辆车辆。ECD之间通过有线连接,能够从周围获取交通信息(如绿灯时间(tl)、车道状态(ls))以及车辆状态(如速度(v)、行驶方向(d)、当前车道(cl)、到十字路口的距离(dc)、导航目标和车辆类型(t))
通过无线通信与周边的ECD和车辆进行连接。因此,当任意车辆驶入十字路口时,ECD将根据该车辆的行驶方向、位置以及周边交通信息,向其发送速度建议并为其选择最佳车道。例如,一辆汽车从右侧区域驶来(通过红色虚线连接到ECD的车辆),希望在交叉路口右转。当相应的ECD获取到该车辆的状态后,ECD会向车载自动驾驶系统发送一个数据包,提示“请切换至中间车道以绕行禁行道路”,因为目标道路已关闭,而最右侧车道为公交专用道。此外,重新规划的路线也包含在该数据包中(由于路径规划不在本文范围内,我们仅转发来自云端的规划结果)。
为了实现对每辆行驶车辆的实时响应,ECLSS的调度器被部署在ECD中,用于计算最优的车辆车道,并通过无线方式将结果与交通信息一起发送给每辆车。因此,我们将ECD中的任务集表示为F={f0, f1…fn},其中n是ECD通信范围(R)内的车辆数量。车辆ID按照距离十字路口的距离升序排列,因此车辆0是距离十字路口最近的车辆(或第一个进入ECD通信范围的车辆),而车辆n是最远的车辆(或最后一个进入ECD通信范围的车辆)。车道数量记为L;nj表示车道j上的最后一辆车,|nj|表示车道j上的车辆数量。每个任务fi∈F是一系列操作,包含四个过程:感知道路状况、车辆向ECD的数据上传、算法计算以及将结果发送给每辆车。
然后,每个任务fi∈F由{tli, dsi, vi, di, cli, dci}表征,这些参数的描述如下:
- tli是绿灯持续的时间,当信号灯为黄灯或红灯时绿灯持续时间为零;此外,当信号灯为绿色时,车辆只能直行或左转;
- dsi={on, off}是方向状态,在此状态下,当dsi=off时,车辆无法驶向其目标方向。
- vi是车辆
的行驶速度。此外,ECLSS中每辆车的最大速度为V;
- di{driving, right, left}表示车辆
希望行驶的方向,包括直行、右转和左转三种选择;
- cli是车辆i所在的车道编号,且仅当车道li为左转车道时车辆才可左转;否则若要直行,则必须切换至中间车道。此外,车道总数记为L;
- dci是车辆i到十字路口的距离;并且
- ti={ordinary, special}是车辆的类型。当i为特殊车辆(如救护车)时,其他车辆需要为其让行。此外,特殊车辆在道路未封闭时可在任意车道行驶。
然后,直行车辆可描述如下:在ti期间,车辆i以速度vi在车道cli上行驶,目标方向为di。随后,ECD将根据其采集的信息计算车辆i的解决方案,并更新dki、clki、tlki、vki和dcki。例如,当ECD获取tli>dci/vi和dsi=off后,可根据以下指令进行更新:请在第k次变道时,以平均速度vki变道至方向dki的clki车道;变道后,通过十字路口的剩余行驶距离为dcki。
4. 车道调度调度问题
在自动驾驶中存在两个潜在的约束:(1)直行车辆需要遵守交通规则;以及(2)自动驾驶的主要任务是确保人员安全。因此,车道调度中的挑战可以总结如下:
- A碰撞可能发生当车辆切换其车道时。如何才能安全地实现变道?
- A车辆只有在十字路口处的对应车道交通信号灯为绿色时才能转弯。如何使车辆快速且有序地通过?
- 普通车辆必须为特殊车辆(如救护车和消防车)让行,以便它们能够快速通过十字路口。如何相应地安排普通车辆的车道切换?
为保证直行的安全,我们将安全距离定义如下:
定义 1. 安全距离(Sd) 是为确保直行安全,两辆相邻车辆之间所需的最小距离。
图2是车辆k想要切换到左转车道时所需安全距离的一个示例;那么,目标车道中相邻车辆i和j之间的距离必须满足
$$
Sd \leq dc_j - dc_k, \
Sd \leq dc_k - dc_i, \
\text{s.t. } v_i \geq v_k \geq v_j.
$$
(1)
同样,同一车道内的车辆在所有车辆的间距和速度满足时是安全的
$$
Sd \leq dc_j - dc_i, \
\text{s.t. } v_i \geq v_j.
$$
(2)
我们使用时间开销T来评估ECLSS的性能,该时间开销定义为最后一辆车到达由ECD调度确定的目标方向的时间。然后,当通信范围R内的车辆数量为|n|,车辆i的车道切换次数为Ki,影响车辆i的车道切换次数为Ii,第j次对时间消耗的影响为Cj,第k次变道时的行驶距离为Δk,在信号灯处等待的时间消耗为ℵi时,我们可以得到时间开销为
$$
T = \max\left{ \sum_{k=0}^{K_i} \frac{\Delta k_i}{v k_i} + \sum_{j=0}^{I_i} C_j + \aleph_i, i \in n \right},
$$
(3)
其中
$$
\Delta k_i = dc^{k-1}_i - dc^k_i, \quad k > 0.
$$
(4)
此外,每辆特殊车辆i必须在一定时间si内通过十字路口,即
$$
\sum_{k=0}^{K_i} \frac{\Delta k_i}{v k_i} + \sum_{j=0}^{I_i} C_j + \aleph_i \leq s_i.
$$
(5)
因此,当ECDs获取交通信息F且十字路口周围的车辆数量为n时,我们的目标是在公式(1)、(2)和(5)的约束下,以最小T调度车辆到达目标方向。
为了便于分析,我们忽略换道所产生的额外距离,因为它是一个较小的固定值,并且可以通过勾股定理轻松计算。

5. 调度
为了提高车辆通过十字路口的速度,并在满足公式(1)、(2)和(5)约束条件下减小T,本文提出了两种车道调度算法(高效切换算法和特种车辆车道切换算法),用于十字路口周围车辆的调度。所提出的方法能够基于ECD的全局视图为每辆车辆选择车道。车辆在[0, V]范围内以与前方车辆相同的速度行驶,同一条车道上前后两车之间的距离在ECLSS中设定为Sd(可通过自适应巡航轻松实现);因此,我们的目标可转化为减少变道的时间开销,使车辆在ECLSS中快速通过十字路口,即让n辆车辆以最小T到达各自的目标方向。
我们将每一次变道分为三个部分:(1)车辆i及其后方的车辆停止行驶,直到前方车辆(包括最前面的车辆)驶离至安全距离Sd;当车辆i前方无车时,车辆i以速度V行驶;(2)随后,车辆i开始以与前方车辆相同的速度行驶;(3)当车辆i与其后方车辆之间的距离达到安全距离Sd时,其后方的车辆开始以与车辆i相同的速度行驶。第k次变道的等待时间开销记为βki。
为了减少时间开销,我们必须提高变道效率并减少等待转弯的时间。如图3所示,当k在等待时,h可以直接变道。因此,我们可以发现时间开销T受到车道切换次数Ki、等待的时间开销βki、到十字路口的距离dci以及交通灯的时间开销ℵi的影响。由于等待交通灯的时间消耗由与∑Kik=0 βki相关的变量表示,当红灯持续α秒且绿灯持续η秒时,我们可以计算ℵi为
$$
\aleph_i = \left\lfloor \frac{\alpha \left( \sum_{k=0}^{K_i} \beta k_i + \sum_{j=0}^{I_i} C_j + \frac{dc_i}{V} \right)}{\eta} \right\rfloor.
$$
(6)
然后,我们可以将式(3)重写为
$$
T = \max\left{ \sum_{k=0}^{K_i} \beta k_i + \frac{dc_i}{V} + \sum_{j=0}^{I_i} C_j + \left\lfloor \frac{\alpha \left( \sum_{k=0}^{K_i} \beta k_i + \frac{dc_i}{V} \right)}{\eta} \right\rfloor, i \in n \right},
$$
(7)
因此,我们车道调度算法的 核心思想 是通过一种协调方法来优化Ki, Ii, Cj 与βki之间的关系,以减少T。
引理 1.
Ki对T的影响与和车辆i的相邻车辆的距离有关。
证明。
我们基于相邻车辆的距离,通过分类讨论来证明该引理。根据公式(1)和(2),我们发现当相邻车辆的距离大于Sd时,切换不会增加时间开销;即T保持不变。当i是当前车道的最后一辆车且其他车道更快时小于当前距离时,T减小;然而,当距离小于Sd时,后方车辆必须减速以保证安全直行距离;此时,T增大。因此,Ki对T的影响与和i相邻车辆的距离有关。 □
引理1揭示了切换仅影响车辆i及其后方的车辆。因此,当车辆i行驶在无法通向其目标方向的车道上(cli ≠ di ∩ dsi = on)或目标方向已关闭时(cli = di ∩ dsi = off),在未引入额外时间开销的情况下,车辆i应尽可能进行切换。
定理 1.
当目标车道中存在位于该车辆前部和后部的车辆时,每次切换所产生的额外时间开销T′与执行切换的车辆位置无关。
证明。
当车辆k想要变道,且车辆k前后均有车辆时,我们将k前方的车辆记为i,后方的车辆记为j。如图2所示,右转车道中的额外时间开销产生于
$$
Sd \geq dc_k - dc_i,
$$
(8)
然后,ECD发送消息以调整这三辆车辆的速度,确保变道的安全性,并产生等待开销βk
$$
\beta_k = \frac{Sd - (dc_k - dc_i)}{V}.
$$
(9)
右转车道上的额外时间开销是
$$
T’ = \frac{Sd - (dc_k - dc_i) + Sd - (dc_j - dc_k)}{V} + \aleph_j = \frac{2Sd + dc_i - dc_j}{V} + \aleph_j = \frac{Sd}{V} + \aleph_j.
$$
(10)
由于ℵj与dck无关,因此可以得出结论:当目标车道前后均有车辆时,切换的车辆位置与额外时间开销T′无关。 □
根据目标车道的交通状况,我们可以获得βki作为
$$
\beta k_i =
\begin{cases}
\frac{Sd - (dc_k - dc_i)}{V}, & \exists j, dc_i - dc_j \leq Sd \
0, & \nexists j, dc_i - dc_j \leq Sd
\end{cases}
$$
(11)
显然,当目标车道中没有车辆j满足dci − dcj ≤ Sd时,不会产生时间消耗。此外,我们将β = 0的情况称为最优变道,将0 ≤ β < Sd/V的情况称为高效变道。根据公式(11),我们将对应第i个阻塞的车辆记为bi,βbi是bi对车辆j造成的延迟;那么,车辆j前方变道所引起的阻塞为
$$
\sum_{i=0}^{I_j} C_j = \sum_{i=0}^{I_j} \beta b_i.
$$
(12)
Based on Lemma 1 and Eq.(11), we can obtain the following result.
定理 2.
对于每辆车辆i,通过时间开销的范围以通过十字路口是
$$
\left[ \frac{dc_i}{V} \left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor \right), \frac{((i + L - 1)Sd + dc_i)\left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor\right)}{V} \right].
$$
证明。
公式(11)表明,当dci − dcj ≤ Sd范围内不存在车辆j时,车辆i可以无减速变道。因此,考虑交通灯造成的阻塞时间消耗后,可得车辆i通过十字路口的最小时间开销为
$$
\frac{dc_i}{V} \left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor \right).
$$
(13)
相比之下,当车辆i的第k条目标车道中存在车辆j满足dci = dcj时,车辆i需要等待Sd/V。因此,在最坏情况下,车辆i需要切换Ki = L − 1次才能到达最终车道。也就是说,切换开销的最大时间对于i是
$$
\frac{Sd(L - 1) + dc_i}{V}.
$$
(14)
由于切换仅发生在的前方,它可能导致延迟,i,且最大等待成本为Sd/V。然后,总阻塞时间消耗为
$$
\frac{i \times Sd}{V}.
$$
(15)
此外,由于需要等待十字路口的绿色信号灯才能通过,因此通过十字路口的最大时间开销是
$$
\frac{((i + L - 1)Sd + dc_i)\left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor\right)}{V}.
$$
(16)
因此,对于每辆车辆i,通过十字路口的时间开销范围为
$$
\left[ \frac{dc_i}{V}\left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor\right), \frac{((i + L - 1)Sd + dc_i)\left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor\right)}{V} \right].
$$
□
当定理2中的车辆i是n的最后一辆车时,我们发现时间开销T的范围是
$$
\left[ \frac{dc_n}{V}\left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor\right), \frac{((n + L - 1)Sd + dc_n)\left(1 + \left\lfloor \frac{\alpha}{\eta} \right\rfloor\right)}{V} \right].
$$
然而,T = ((n + L − 1)Sd + dcn)(1 + ⌊α/η⌋)/V过于悲观。由于每辆车i的车道切换次数由cli和di确定,我们可以通过减少∑Iij=0 Cj来优化T。
基于上述结果,我们提出了高效切换搜索算法(SESA),通过广度和深度搜索来实现高效变道,以减少T。SESA的伪代码见算法1,其中cl*i为变道一次后的车道。注意
算法 1 寻找高效切换算法。
要求:F; 确保:所有车辆到达其目标方向;
1: 为每辆车辆Ki计算i;
2: 当(clj ≠ dj ∩ dsj = on) ∩ (clj = dj ∩ dsj = off) = ∅, j ∈ n时执行
3: for i = 0 to |n| 执行
4: if cli ≠ di then
5: if ∃p ∈ n满足clp ≠ dp ∩ dcp ∈ [dci − Sd, dci + Sd] ∩ ((clp, cl
p) ∩ (cli, cl
i)) then
6: 切换p和i;
7: else if dci = (Ki − k)Sd then
8: 切换p和i;
9: end if
10: for 车道的clq其中有车辆切换执行
11: if ∃p ∈ n满足clp ≠ dp ∩ dcp > dcq then
12: 切换p和i;
13: end if
14: end for
15: 更新车辆信息并计算T by Eqs. 7和11;
16: end if
17: end for
18: end 当
19: 返回T;
算法1是执行SESA一次的情况,并且SESA被反复执行以调度新检测到的车辆。
SESA首先根据ECD传输范围内的车辆和交通信息计算每辆车的变道顺序(第1行);然后判断每辆车是否在朝其目标方向行驶的车道上,若判断为真,则返回T(第2行)。如果存在需要变道的车辆,SESA将通过广度和深度搜索寻找高效切换以减少T(第3–18行)。当车辆i所在车道无法通向其目的地时,系统将在相关车道范围内[dci − Sd, dci + Sd]搜索希望变道的车辆;然而,当前当i的切换不属于高效变道时,表示在同一时间段内没有车辆可以进行切换(第3‐6行)。然后,i的切换只能在dci = (Ki − k)Sd时发生(第7‐9行)。当SESA确定了需要切换的车辆及其对应的车道(包括当前车道和切换后的车道)后,将通过深度搜索来减少T,以实现高效变道(第10‐14行)。车辆信息和T将根据公式(7)和(11)进行更新(第15‐18行)。最后,SESA返回T(第19行)。SESA的时间复杂度为O(n log n)。
定理 3.
该时间开销T最多可减少⌊y(L−1)/L⌋ + ⌈⌊y(L−1)/L⌋/η⌉α,其中y是高效切换的数量。
证明。
每次切换的时间消耗在0 ≤ β < Sd/V范围内。因此,当……时,时间开销的减少达到最大值。由于最多有(L − 1)个高效切换可以同时发生,高效切换的最大时间节省为
$$
\left\lfloor \frac{y(L - 1)}{L} \right\rfloor.
$$
(17)
此外,时间节省可能使车辆在另一次红灯出现前通过十字路口;也就是说,交通灯带来的附加时间节省为
$$
\left\lceil \frac{\left\lfloor \frac{y(L - 1)}{L} \right\rfloor}{\eta} \right\rceil \alpha.
$$
(18)
因此,该时间开销T最多可减少⌊y(L−1)/L⌋ + ⌈⌊y(L−1)/L⌋/η⌉α,其中y是高效切换的数量。 □
考虑到特种车辆的特点,我们提出了特种车辆车道切换算法(SVLSA),以确保特种车辆能在截止时间前通过十字路口。SVLSA的伪代码见算法2。
算法 2 特殊车辆车道切换算法
Require: F; 确保:通过十字路口的特殊车辆满足式5;
1: 为每辆车辆Ki计算i;
2: 当(clj ≠ dj ∩ dsj = on) ∩ (clj = dj ∩ dsj = off) = ∅, j ∈ n时执行
3: for i = 0 to |n| 执行
4: if ti = special then
5: si = si − dci/V;
6: 计算ℵi;
7: if ∃p ∈ n满足clp ≠ dp ∩ dcp < dci ∩ (clp = cli ∪ cl
p = cli) then
8: 通过βp公式11进行计算;
9: if si − βp − ℵi ≥ 0 then
10: 更新ℵi并更新其余si;
11: 切换p;
12: end if
13: end if
14: else if ∃p满足tp = special ∩ dcp ≥ dci ∩ (cli = cp ∪ cli
= cp) then
15: 根据公式6和11计算ℵi和βi;
16: if sp − βi − ℵi ≥ 0,则
17: 更新ℵi和剩余的si;
18: 切换p;
19: end if
20: else
21: 按照SESA执行;
22: end if
23: end for
24: end 当
6. 实验结果
在本节中,我们将所提出的方法与实际驾驶情况下的变道进行比较。我们将实际真实场景中的变道方法称为无调度变道(LSWS)。在LSWS中,车辆仅根据自身信息(例如车辆i的行驶方向以及前车的速度)来决定是否变道。此外,在LSWS中,当车辆需要变道时会立即执行,且不考虑其他车辆的减速情况。也就是说,LSWS下的车辆采用局部最优方法进行调度。所有算法均使用C语言实现,程序运行在配备3.4GHz CPU和8GB内存的Windows机器上。
为了说明我们算法的适用性,针对每种参数配置,随机生成了多个测试用例。对于每个测试用例,我们将安全距离设置为Sd = 10 m,最大速度为V = 10 m/s。在每种情况下,均有一条左转车道和一条右转车道,特种车辆数量在[0,3]范围内,红灯持续时间为α = 20 s,绿灯持续时间也为β = 20 s。每次测试开始时,交通灯变为绿灯。此外,每种情况下最多只有一个方向处于关闭状态,想要沿该方向行驶的车辆将更改其目标方向以继续沿道路行驶。代表性的仿真参数总结于表1。


图4显示了L = 5条车道和S = 2辆特种车辆在车辆数量n不同时的时间开销T之间的关系。车辆数量范围从n = 20到60。假设车辆在每条车道上均匀分布,且最大通过时间一辆特殊车辆si = 15 s。这三种方法的时间开销均随着车辆数量的同时增加而增加。然而,增加速率显示出巨大差异。这是因为在开始时,在这三种方法下所有车辆都可以在第一个绿灯期间通过十字路口;由于SVLSA下的车辆可能会错过其方向,并以速度V行驶以保证公式(5),这种错失方向的现象减缓了T的增加速率。使用SESA时,车辆能够高效搜索,所有车辆都将到达其目标方向;因此,这三种方法的增加速率满足LSWS > SESA > SVLSA。当车辆无法在第一个绿灯期间驶向目的地时,剩余车辆必须等待下一个绿灯;因此,T急剧增加,例如在n = 40当Kn = 0.25时。
图5显示了时间开销T与车道数L之间的关系,适用于n = 50车辆、K = 13以及特殊车辆。当仅有一条车道时,所有车辆都通过该车道通过十字路口;因此,这三种方法的时间开销相同;然而,随着车道数的增加,SESA(β)下的切换成本得到优化,并且SVLSA下切换受到限制(si − β − ℵi ≥ Sdi/V)。因此,T减小并满足LSWS > SESA > SVLSA。

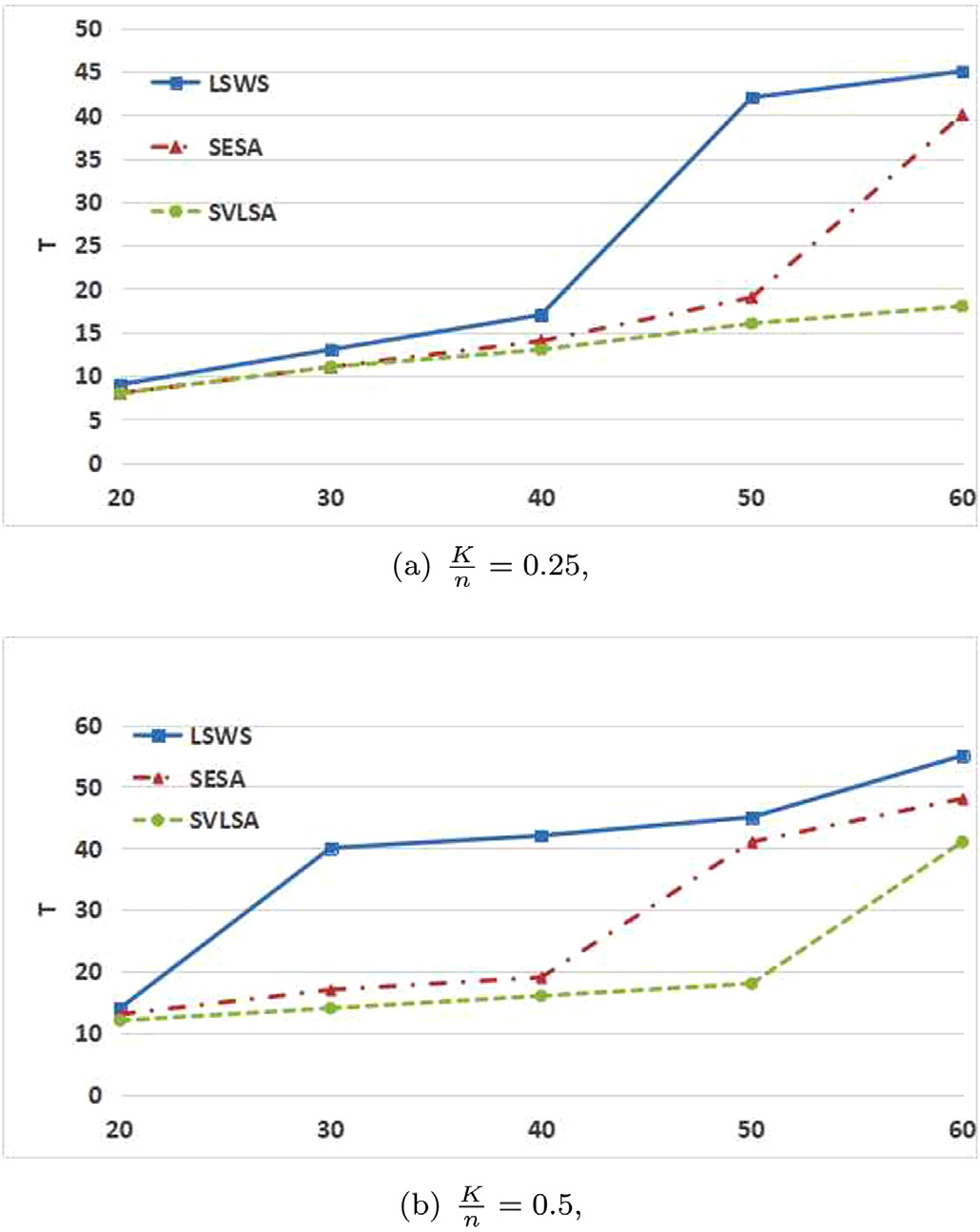
图6展示了在L = 5条车道、K = 13和n = 50辆车的情况下,时间开销T与特种车辆数量S之间的关系。考虑了特种车辆数量在S = 0到S = 5之间的变化。在LSWS和SESA下,随着S的变化,时间开销保持不变。对于SVLSA,在S = 0和S = 1时,其时间开销与SESA相同。考虑到特种车辆的通行时间,SVLSA牺牲了部分车辆到达其目标方向的机会。也就是说,随着S的增加,SVLSA减少了β和∑Iji=0 Cj。因此,时间消耗与S成反比。
图7显示了在L = 5条车道、n = 50辆车辆和S = 2辆特种车辆的情况下,时间开销T与交换次数K之间的关系。图7中的时间开销增长速度比图4更快,这说明切换所消耗的时间比直行驾驶更多。与上述结果类似,SVLSA的时间开销仍然低于其他两种方法。
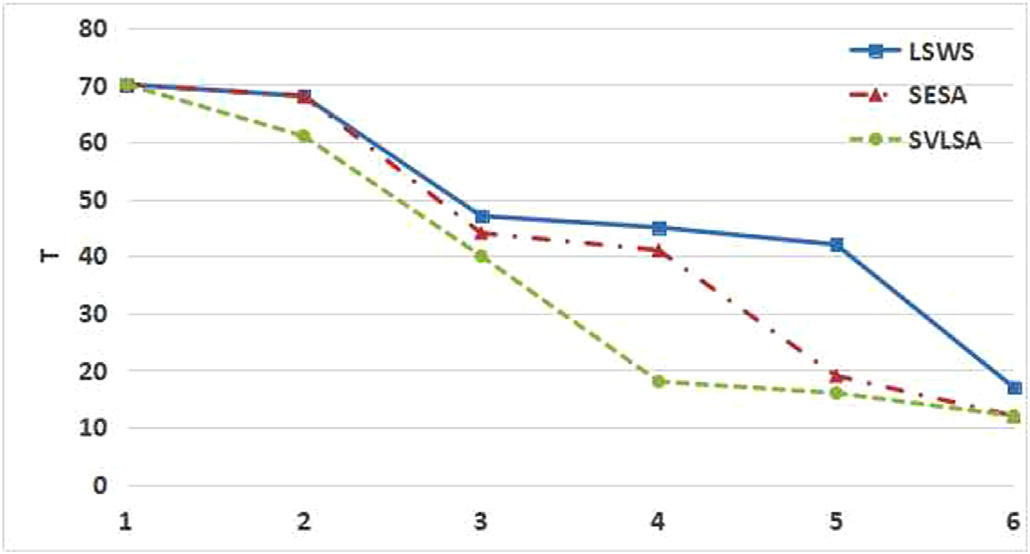
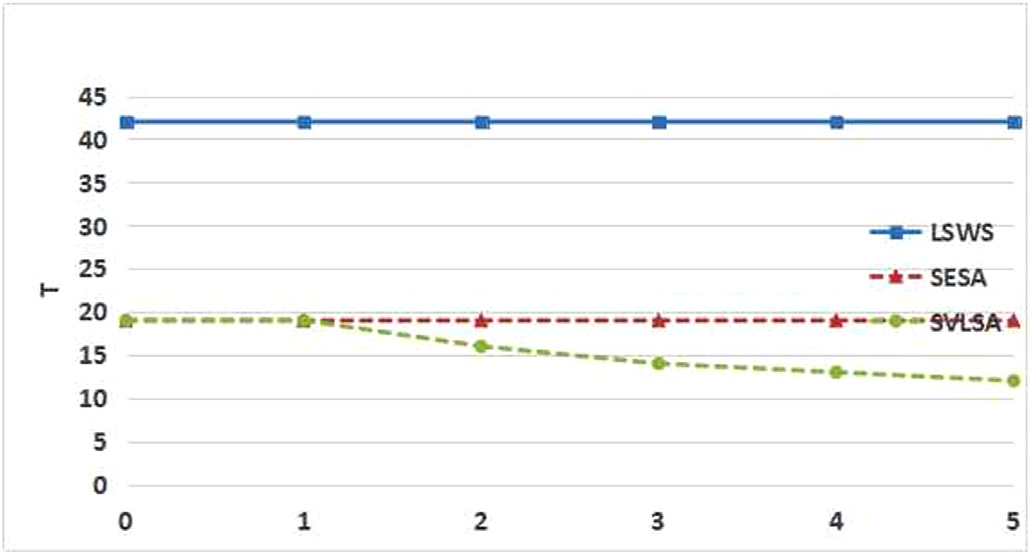
图8显示了时间开销T与特种车辆si的最大通过时间在n = 50车辆、L = 5车道和S = 2特种车辆情况下的关系。最大通过时间si以5为单位从5变化到25。时间开销随着si的增加而增加。原因是特种车辆有更多的时间通过十字路口,从而导致其他车辆需要切换并产生额外的时间消耗。当该值达到25时,特种车辆的影响不再紧迫(所有切换均可发生并满足公式(5)),此时退化为SESA。
与从图8相比,我们模拟了错过行驶方向的车辆数量与车辆数量之间的关系D以及车辆数量与
7. 结论
本文提出了一种名为基于边缘计算的车道调度系统的新型模型,用于研究十字路口周围车辆(包括普通和特种车辆)的车道调度问题。在ECLSS中,多个边缘计算设备(ECD)被部署在十字路口周围,用于收集来自车辆和道路状况的信息。我们的模型包含三个层次(车辆、ECD和云端),主要关注第二层(ECD),因为已有部分相关工作聚焦于其他两层。基于ECD的集中式管理,提出了两种面向边缘计算的自动驾驶车道调度方法(SESA和SVLSA),分别用于实现车辆高速通过十字路口,并确保特种车辆在特定时间内通过十字路口。进行了大量仿真,仿真结果表明,在真实车道切换场景(LSWS)中,所提出的方法相比竞争方案具有优越性。
所提出的ECLSS可以通过引入部署的基础设施(如摄像头、交通云和基站)进一步扩展。针对包含和不包含特种车辆的算法,其车道调度方法可被扩展以解决在部署此类基础设施时的调度问题。其内在问题是:如何在这些基础设施之间实现按需的计算和通信资源分配,以满足不同车辆的额外需求,这些基础设施虽能提供更高的计算能力,但也存在链路持续时间短和带宽限制的问题。此外,关于车道的详细信息在ECLSS中的切换是进一步减少车辆通过十字路口时间开销的有效方法,例如对阻塞时间消耗的详细讨论。最后,天气是影响交通信息的关键因素;因此,确定一种利用云计算和边缘计算分析交通信息以动态调整安全距离的方法也非常重要。解决上述问题也是未来研究的另一个潜在方向。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








