SVPWM 扇区判断法和七段式实现

原创已于 2025-12-28 23:41:20 修改 · 743 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#单片机 #嵌入式硬件

于 2025-12-28 23:40:01 首次发布

电机笔记专栏收录该内容

23 篇文章

订阅专栏

一、SPWM 的低效问题

效率详细讨论与推导请看我之前写的：

SPWM 与 SVPWM (零序分量法实现) 电压利用率简谈_svpwm电压利用率-优快云博客

调制效率问题非本篇主要内容，在这里忽略细节，直接抛出结论。

1.1 电压利用率定义

电压利用率 = 逆变器能输出的最大相电压 (峰值，非峰峰值) 除母线电压

1.2 SPWM 电压利用率

下图是我们使用 SPWM 的相电压：

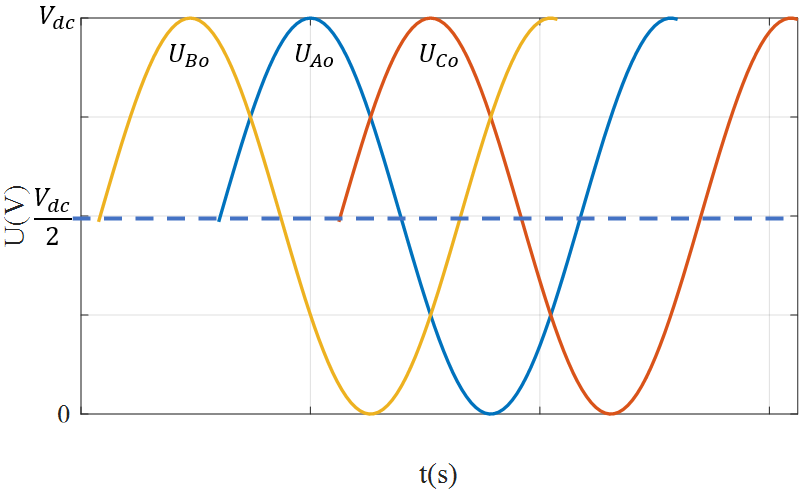
可见，其相电压利用率为 50%，也就是 0.5，我们可见每一项的峰值只有母线电压的一半。

我们可知：

$V_{line}=\sqrt{3}V_{ph}$

$V_{line}$ = 线电压
$V_{ph}$ = 相电压

所以，SPWM 的线电压利用率就是 0.5 乘 $\sqrt{3}$ ，也就是 86.6%。

1.3 SVPWM 电压利用率

SVPWM 通过将相电压改成马鞍波形式，使其相电压利用率达到 $\frac{1}{\sqrt{3}}\approx 0.577$ 。

这样，我们再将其转化为线电压，就得到了 $\sqrt{3}\times \frac{1}{\sqrt{3}}=1$ 的电压利用率了。

下图中两个调制波形的效率比相同，调制比均为 86.6%。

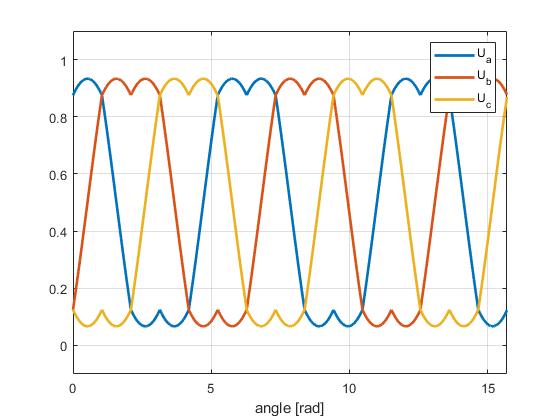
我们根据上图来看，母线电压是 1V，这样相电压最大为 1V 最小为 0V。我们保证波形不削顶的情况下，SPWM 的线电压最大极限也只有 1V * 86.6% = 0.866 V。

但是 SVPWM 的马鞍波在调制比 86.6% 的情况下，顶部没有触及到 1V，同时底部也没有触及到 0V，其还有13.4%的调制余量。所以在波形上我们可以看到，为什么 SVPWM 的电压利用率能达到 100%。

二、SVPWM 扇区判断法实现 (dq 轴转化 SVPWM)

2.1 六步换相控制

六步换相控制电机原理如下：

其中我们通过 A-B、A-C、B-C、B-A、C-A、C-B 通电六种组合，可以得到转子的六个角度：

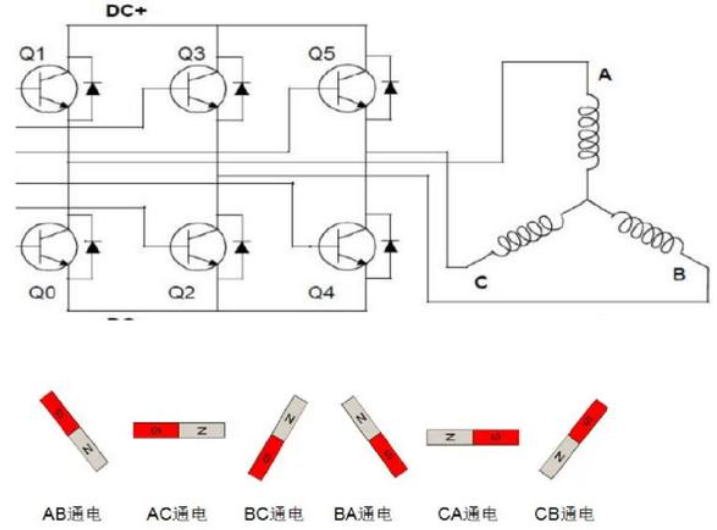
将电机转子的六个角度分为 V1 ~ V6 六个角度，也可以理解为六个基本向量，如下图：

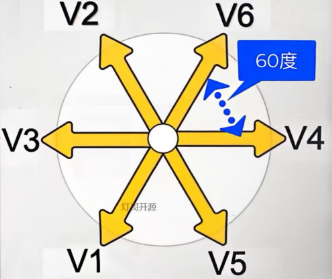
我们将 V6 定义为 110，也就是上管 T1 和 T3 打开，下管 T2 打开；

我们将 V4 定义为 100，也就是上管 T1 打开，下管 T6 和 T2 打开；

如下图所示：

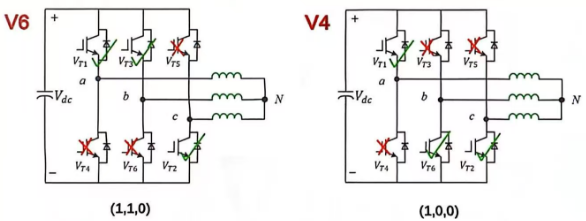
2.2 电压关系分析

我们应该根据 Y 形连接中的中点电压作为 0V 电压参考，因为转子所受的安培力也是为这个线圈节点的计算。

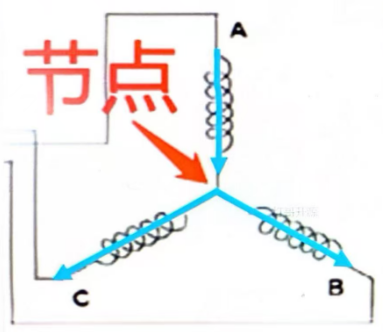
我根据电路仿真我们可知 Y 形连接的电压关系，在下模型中，我们将线圈等同于 1 欧电阻。

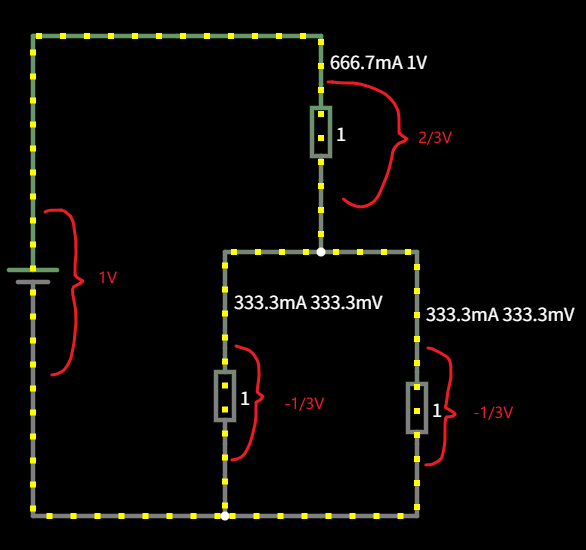
根据基尔霍夫电流定律可知：

$I_{a}+I_{b}+I_{c}=0$

同理，根据基尔霍夫电压定律可知：

$U_{a}+U_{b}+U_{c}=0$

在上面的模型中，A 相为 $U_{a} = \frac{2}{3}V$ ，则 $U_{b} = -\frac{1}{3}V$ ， $U_{c} = -\frac{1}{3}V$ 。

2.3 SVPWM 数学推导

当然，我们的控制不能满足于六个角度，所以我们单独分析 V6 和 V4 两个基本向量夹角，以求得更细分的角度控制。

如下图所示，这是 V6 和 V4 区间的细分示意：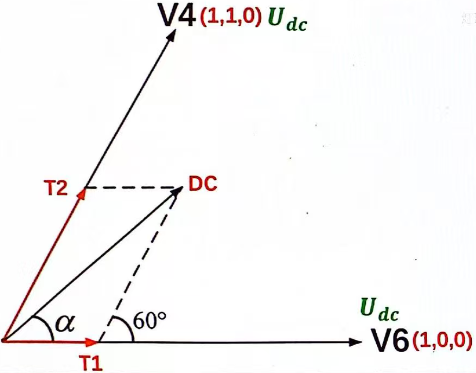

其 DC 可以看作目标的 Uq 电压，也就 q 轴磁场的强度；T 是单位周期，周期中 T = 1。

根据正弦定理 (在任意一个平面三角形中，各边和它所对角的正弦比的比相等)，我们可以得到：

$\frac{\dfrac{T_1}{T_s}\,|V_6|}{\sin(60^\circ-\alpha)} = \frac{\dfrac{T_2}{T_s}\,|V_4|}{\sin(\alpha)} = \frac{|DC|}{\sin(120^\circ)}$

$|V_6|$ = 等同于 Udc 电压
$|V_4|$ = 等同于 Udc 电压
$T_{1}$ = V6 方向施加的电压
$T_{2}$ = V4 方向施加的电压
$T_{s}$ = 总周期
$DC$ = 向量电压

如果我们要生成一个 DC 的矢量，下面两个公式可以得到 T1 和 T2 的长度。

$\begin{cases} T_1 = \frac{2\sqrt{3}}{3}\cdot \frac{|DC|}{U_{dc}}\cdot T_s \cdot \sin(60^\circ-\alpha) \\ T_2 = \frac{2\sqrt{3}}{3}\cdot \frac{|DC|}{U_{dc}}\cdot T_s \cdot \sin(\alpha)\end{cases}$

$T_{1}$ = V6 方向施加的电压
$T_{2}$ = V4 方向施加的电压
$T_{s}$ = 总周期
$DC$ = 电压向量
$U_{dc}$ = 母线电压
$\alpha$ = 目标角度
$\frac{2\sqrt{3}}{3}=\frac{1}{\sin (120^{\circ})}$

我们可知，Uq、Ud 的矢量的模长度和 Uα 和 Uβ 矢量的和的模长度是相同的：

$\sqrt{U_{q}^{2}+U_{d}^{2}} = \sqrt{U_{\alpha }^{2}+U_{\beta }^{2}}$

$U_{dq}$ = d、q 轴电压
$U_{\alpha \beta }$ = α、β 轴电压

但是根据等幅克拉克变换来说，A、B、C 三项的电压却要乘 2/3。

$\begin{bmatrix} u_\alpha \\ u_\beta \end{bmatrix} = \frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} u_a \\ u_b \\ u_c \end{bmatrix}$

所以，最终的变换关系如下：

$\begin{cases} T_1 = \frac{2\sqrt{3}}{3}\cdot \frac{3}{2}\cdot \frac{\sqrt{U_{q}^{2}+U_{d}^{2}} }{U_{dc}} \cdot \sin(60^\circ-\alpha) \\T_2= \frac{2\sqrt{3}}{3}\cdot \frac{3}{2}\cdot \frac{\sqrt{U_{q}^{2}+U_{d}^{2}} }{U_{dc}} \cdot \sin(60^\circ) \end{cases}$

$\sqrt{U_{q}^{2}+U_{d}^{2}}$ = 等幅我们的 DC 电压向量
$U_{dc}$ = 母线电压
$\alpha$ = 目标角度
$\frac{2}{3}$ = 等幅克拉克变换
$\frac{2\sqrt{3}}{3}=\frac{1}{\sin (120^{\circ})}$

因为我们是 id = 0 控制，综合化简后得：

$\begin{cases} T_1 = \sqrt{3}\cdot \frac{U_{q}}{U_{dc}} \cdot \sin(60^\circ-\alpha) \\T_2 = \sqrt{3}\cdot \frac{U_{q}}{U_{dc}} \cdot \sin(\alpha) \end{cases}$

$U_{dc}$ = 母线电压
$U_{q}$ = q 轴电压
$\alpha$ = 目标角度

2.4 推广至六个向量

对角度取整，确定指定角度在哪个扇区：

$k = \left\lfloor \frac{\theta}{\pi/3} \right\rfloor + 1, \quad k \in \{1,2,3,4,5,6\}$

k = 扇区
$\theta$ = 当前角度

确定扇区内的目标角度：

$\alpha = \theta- (k-1)\frac{\pi}{3}, \quad 0 \le \alpha < \frac{\pi}{3}$

$\alpha$ = 扇区内角度
$K$ = 扇区

至此，我们的 T1 和 T2 推广至六个扇区：

$\begin{cases} T_1 = \sqrt{3}\cdot \frac{U_{q}}{U_{dc}} \cdot \sin(K\cdot 60^\circ-\alpha) \\T_2 = \sqrt{3}\cdot \frac{U_{q}}{U_{dc}} \cdot \sin(\alpha-(K-1)\cdot 60^\circ ) \end{cases}$

$U_{dc}$ = 母线电压
$U_{q}$ = q 轴电压
$\alpha$ = 目标角度
$K$ = 扇区

最后，我们需要计算出 T0 时间：

$T_0 = 1-T_1 -T_2$

对于 V4 和 V6 向量之间，我们的开关顺序是这样的：

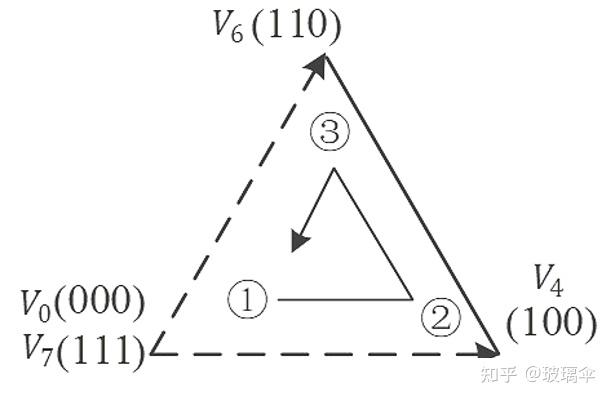
以上是讨论一个扇区的，所有扇区的开关切换顺序可以由下图来表示：

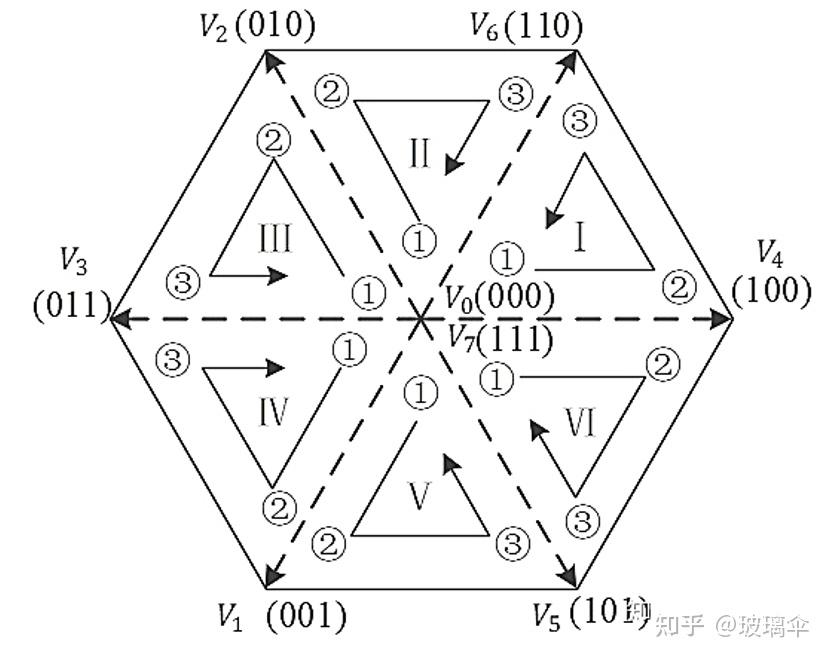
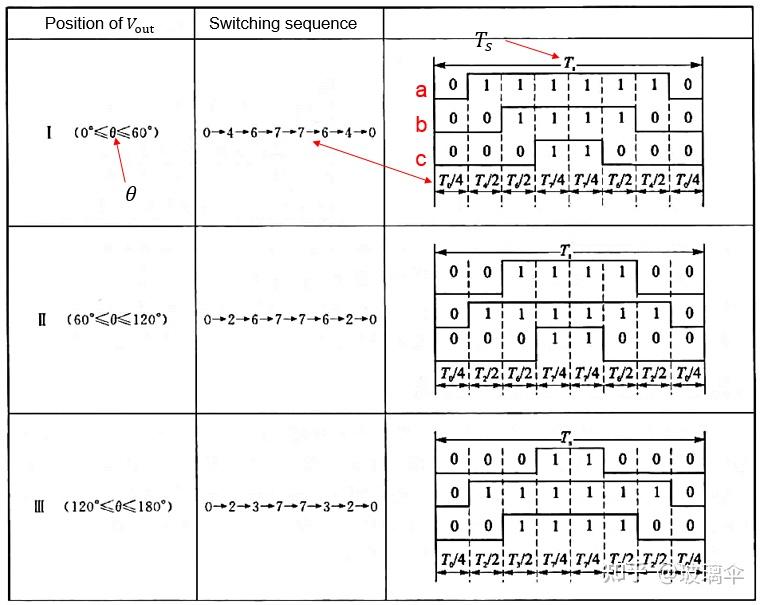
开关顺序表如下：

所谓七段式，也就是每个调制周期切换七次。

2.5 代码演示

void M1_setTorque(float Uq, float angle_el)
{
  // 如果 q 轴电压为负，等价于电压矢量反向 180°
  // 这样后面统一用正幅值处理
  if (Uq < 0)
    angle_el += _PI;

  // 只保留电压幅值（方向已体现在 angle_el 中）
  Uq = abs(Uq);

  // dq 坐标系 → αβ 坐标系
  // 在 FOC 中：q 轴比 α 轴超前 90°
  // 因此需要 +π/2
  angle_el = _normalizeAngle(angle_el + _PI_2);

  // 根据 αβ 电压角度判断 SVPWM 扇区
  // 每个扇区宽度 π/3（60°）
  // sector ∈ {1,2,3,4,5,6}
  int sector = floor(angle_el / _PI_3) + 1;

  // ================= SVPWM 核心：计算 T1 / T2 =================

  // T1：当前扇区中“后一个”有功矢量的作用时间
  // √3 来自 SVPWM 电压增益
  // sin(k·π/3 − θ) 是几何投影关系
  float T1 = _SQRT3 * sin(sector * _PI_3 - angle_el) * Uq / voltage_power_supply;

  // T2：当前扇区中“前一个”有功矢量的作用时间
  float T2 = _SQRT3 * sin(angle_el - (sector - 1.0) * _PI_3) * Uq / voltage_power_supply;

  // T0：零矢量时间（剩余时间）
  // 一个 PWM 周期被归一化为 1
  float T0 = 1 - T1 - T2;

  // 三相 PWM 占空比（归一化 0~1）
  float Ta, Tb, Tc;

  // ================= 根据扇区分配 T1 / T2 / T0 =================
  // 采用“中心对齐 PWM”：
  // 零矢量 T0 均分到前后（T0/2）

  switch (sector)
  {
  case 1:
    // 扇区 1：V1 → V2
    Ta = T1 + T2 + T0 / 2;
    Tb = T2 + T0 / 2;
    Tc = T0 / 2;
    break;

  case 2:
    // 扇区 2：V2 → V3
    Ta = T1 + T0 / 2;
    Tb = T1 + T2 + T0 / 2;
    Tc = T0 / 2;
    break;

  case 3:
    // 扇区 3：V3 → V4
    Ta = T0 / 2;
    Tb = T1 + T2 + T0 / 2;
    Tc = T2 + T0 / 2;
    break;

  case 4:
    // 扇区 4：V4 → V5
    Ta = T0 / 2;
    Tb = T1 + T0 / 2;
    Tc = T1 + T2 + T0 / 2;
    break;

  case 5:
    // 扇区 5：V5 → V6
    Ta = T2 + T0 / 2;
    Tb = T0 / 2;
    Tc = T1 + T2 + T0 / 2;
    break;

  case 6:
    // 扇区 6：V6 → V1
    Ta = T1 + T2 + T0 / 2;
    Tb = T0 / 2;
    Tc = T1 + T0 / 2;
    break;

  default:
    // 理论上不会进入
    Ta = 0;
    Tb = 0;
    Tc = 0;
  }

  // ================= 占空比 → 实际相电压 =================

  // 将归一化占空比乘以母线电压
  // 得到三相等效输出电压
  float Ua = Ta * voltage_power_supply;
  float Ub = Tb * voltage_power_supply;
  float Uc = Tc * voltage_power_supply;

  // 设置 PWM（底层一般是比较寄存器）
  M1_setPwm(Ua, Ub, Uc);
}