Leetcode周赛274记录-基环内向树

题干信息

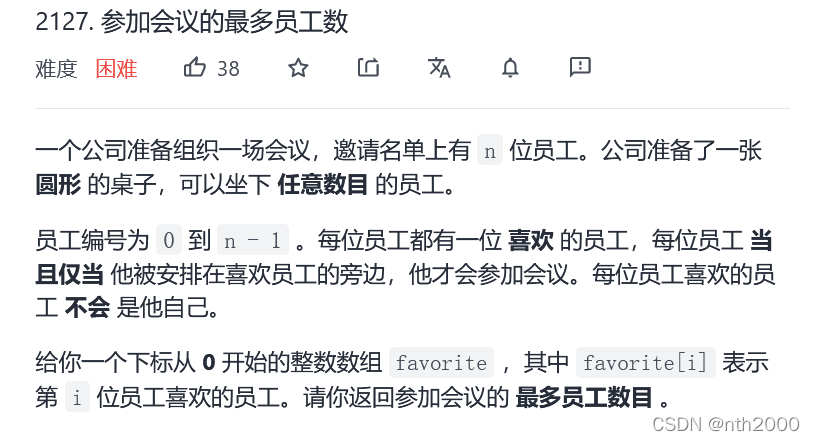
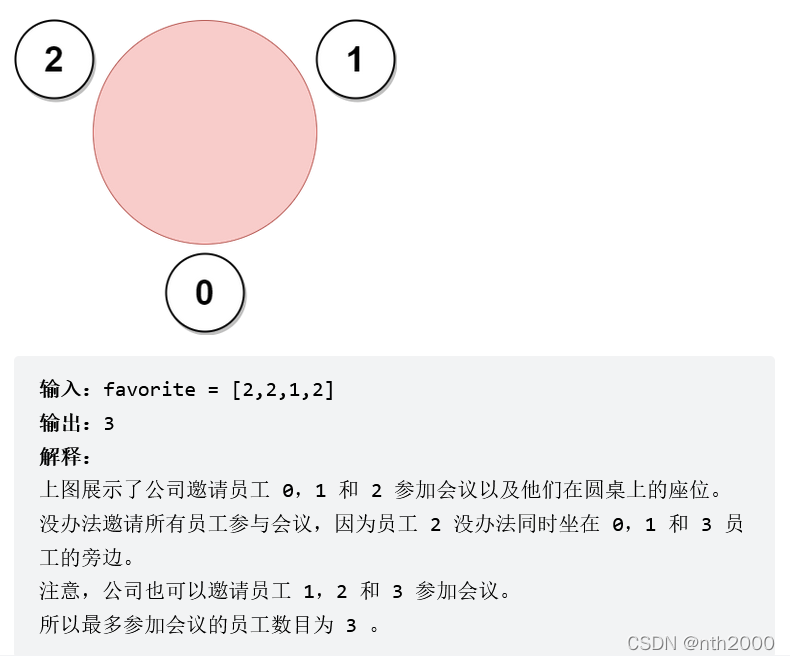
图抽象-基环内向树

• 每个员工视作一个结点，如果员工A喜欢员工B，则从A到B加上一条有向边。从而构成一个有向图。
• 从而这个图有许多的弱连通分量。弱连通分量是指将有向边变为无向边后图的连通分量。
• 对每个弱连通分量而言，假设其顶点数目为$k$，由于每个点仅能发出去一条边，因此边的数量也是$k$。假设不存在环，则由树的充要条件可知边的数目为$k-1$。假设存在大于等于2个的环，若两个环无公共顶点，则这不是一个弱连通分量。若两个环有公共顶点，则对应原始有向图中这个公共顶点的出度为2，矛盾。因此每个弱连通分量有且仅有一个环。
• 综上所述，每个弱连通分量可构成如下结构：
  

求解思路

• 对于每个弱连通分量，其具有唯一的环要么顶点数为2，要么顶点数目大于等于2

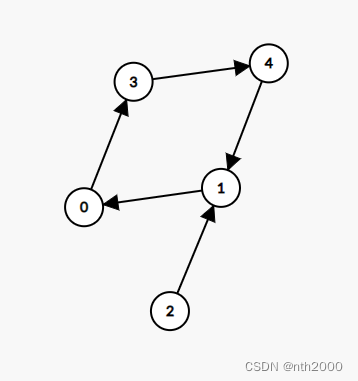
环结点数目大于2的弱连通分量

• 对于环顶点数大于2的弱连通分量，如图所示：

• 在此类型的弱连通分量中环上结点可以围成一桌

• 环上结点间不能插入其他任何非环上结点，否则不满足条件

• 非环结点不能自己组成一桌。可以考虑反证法，假设它们能组成一桌，那么一定会形成一个环，矛盾。

• 而此弱连通分量上的所有结点与其他弱连通分量的任何结点都不能组成更大的一桌。只有这里环上的结点能组成一桌，且环上不能再添加新的结点，否则破坏了喜欢关系。

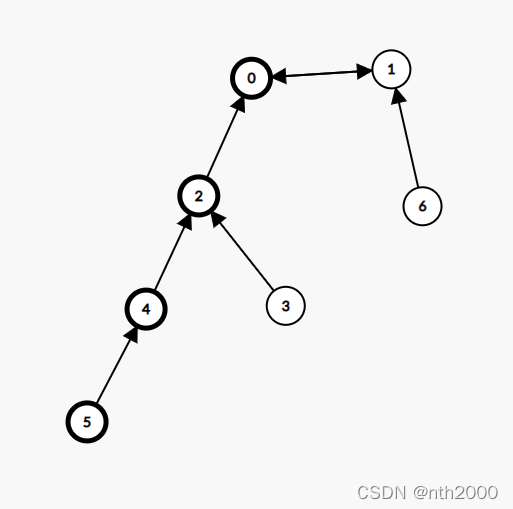
环结点数目等于2的弱连通分量

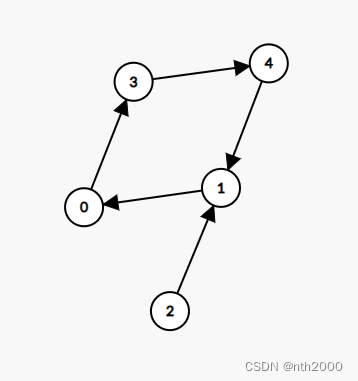
• 对环顶点数目等于2的弱连通分量，如图所示:
• 
• 首先，不在环上的结点肯定不能单独构成一桌，也不能和其他弱连通分量中的结点构成一桌
• 考虑将环上的两个结点先安排在一桌上（图中的0，1结点），且一定要被安排在一起的。由于0喜欢1，1喜欢0，所以0的一侧还可以安排其追随者，这个追随者还可以再安排追随者的追随者，以此类推。1的一侧同理。最后将两个末尾追随者拼接在一起，依旧满足题意，且这对应是该弱连通分量所能安排的最大值
• 除此之外，对于其他环长为2的弱连通分量，都可以将上述末尾追随者首位相连接，得到更多的人数。

求解思路

• 设图中弱连通分量集合为$A$，每个弱连通分量用$G_c\in A$进行表示，其所能围成最大的桌人数为$g(G_c)$，所对应的环长为$f(G_c)$，则最终结果为：max{maxf(Gc)>2∧Gc∈A{g(Gc)},∑f(Gc)=2∧Gc∈Ag(Gc)}max\{ max_{f(G_c)>2 \land G_c \in A } \{g(G_c)\} ,\sum_{f(G_c) = 2 \land G_c \in A} g(G_c)\}max{maxf(Gc​)>2∧Gc​∈A​{g(Gc​)},f(Gc​)=2∧Gc​∈A∑​g(Gc​)}

  • 当$f(G_c)>2$时有$f(G_c)=g(G_c)$
  • 当$f(G_c)=2$时$g(G_c)$等于2加上两个成环结点追随者的最大长度。

• 求$f(G_c)$:先对图执行一次拓扑排序，剩下的所有结点入度均为1。从任意入度为1的结点开始遍历出当前环长度。

• 求$f(G_c)=2$的$g(G_c)$，从环上两个结点开始分别在反向图中寻找追随者的最大深度。

代码实现

class Solution {
    public int dfs(int start,int[] indegree,Map<Integer,List<Integer>> a)
    {
        int ans = 1;
        if(a.get(start) == null)
            return 1;
        for(int b : a.get(start))
        {
            if(indegree[b] == 0)  //不在环上的结点入度为0
                ans = Math.max(ans , dfs(b,indegree,a) + 1);
        }
        return ans;
    }

    public int maximumInvitations(int[] favorite) {
        int[] indegree = new int[favorite.length];
        Map<Integer,List<Integer>> a = new HashMap<>();  //反向图
        for(int i = 0;i<favorite.length;i++)
        {
            //建立反向图
            List<Integer> temp = a.getOrDefault(favorite[i],new ArrayList<>());
            temp.add(i);
            a.put(favorite[i],temp);
            //计算顶点入度
            indegree[favorite[i]]++;
        }
        //topological sort
        Queue<Integer> q = new LinkedList<>();
        //所有入度为0的顶点进入队列
        for(int i = 0;i<favorite.length;i++)
            if(indegree[i] == 0)
                q.add(i);
        while(!q.isEmpty())
        {
            int front = q.poll();
            indegree[favorite[front]]--;
            if(indegree[favorite[front]] == 0)
                q.add(favorite[front]);
        }
        int ans=  0;
        int total = 0;
        //选择入度大于0的顶点找环
        boolean[] visit = new boolean[favorite.length];
        for(int i = 0;i<indegree.length;i++)
        {
            if(indegree[i] > 0 && !visit[i])
            {
                int circle = 1;
                visit[i] = true;
                int j = i;
                while(favorite[j] != i)
                {
                    j = favorite[j];
                    visit[j] = true;
                    circle++;
                }
                if(circle > 2)
                    ans = Math.max(ans,circle);
                else
                    total += (dfs(i,indegree,a) + dfs(j,indegree,a));
            }
        }
        return Math.max(ans,total);
    }

    public static void main(String[] args)
    {
        new Solution().maximumInvitations(new int[]{2,2,1,2});
    }
}