Codeforce8.24-8.28做题记录

Nearest Excluded Points（1900）

题意：
给定n个独特的二维坐标点，找出距离每个点最近汉明距离的不在这些n个独特二维坐标点的整数坐标二维格点。
数据范围：

题解：
没有找到对每个点在Log复杂度内的算法。
事实上，对于距离相邻的点或者说挨在一起的点可以增量更新。
首先距离最近汉明距离为1的点。
再遍历这些点的邻接顶点，一定可以加入一些距离为2的点。
以此类推。每次都可以加入新格点。
迭代到所有点都加入完毕即可。

#include <bits/stdc++.h>
#include <math.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;



int main()
{
	int n;
	cin >> n;
	set<pair<int,int>> m;
	map<pair<int,int>,int> mapp;
	pair<int,int> ans[n];
	for(int i = 0;i<n;i++)
	{
		int x,y; cin >> x >> y;
		m.insert({x,y});
		mapp[{x,y}]=i;
	}
	set<pair<int,int>> m_;
	for(auto& p : m)
	{
		int x = p.first; int y = p.second;
		if(m.find({x+1,y})==m.end()){
			m_.insert({x,y});ans[mapp[{x,y}]] = {x+1,y};
		}
		else if(m.find({x-1,y})==m.end())
		{
			m_.insert({x,y});ans[mapp[{x,y}]] = {x-1,y};
		}
		else if(m.find({x,y-1})==m.end())
		{
			m_.insert({x,y});ans[mapp[{x,y}]] = {x,y-1};
		}
		else if(m.find({x,y+1})==m.end())
		{
			m_.insert({x,y});ans[mapp[{x,y}]] = {x,y+1};
		}
	}
	for(auto &p : m_) m.erase(p.first);
	int dis = 1;
	while(!m.empty())
	{
		set<pair<int,int>> newadd;
		dis++;
		for(auto &p:m_)
		{
			int x = p.first.first,y = p.first.second;
			int ind= mapp[{x,y}];
			int nx = ans[ind].first,ny = ans[ind].second; 
			if(m.find({x-1,y})!=m.end()) {newadd.insert({x-1,y});ans[mapp[{x-1,y}]] = {nx,ny};
			}
			if(m.find({x,y-1})!=m.end()) {newadd.insert({x,y-1});ans[mapp[{x,y-1}]] = {nx,ny};
			}
			if(m.find({x+1,y})!=m.end()) {newadd.insert({x+1,y});ans[mapp[{x+1,y}]] = {nx,ny};
			}
			if(m.find({x,y+1})!=m.end()) {newadd.insert({x,y+1});ans[mapp[{x,y+1}]] = {nx,ny};
			}
		}
		m_.clear();
		for(auto p : newadd) 
		{
			m.erase(p);
			m_.add(newadd);
		}
	}
	for(int i = 0;i<n;i++) printf("%d")	
}

反思：这道题最初想法是看距离相同距离汉明距离上是否有点，但均不能在log复杂度内求解。但注意这里有多个点，看输出看能否增量更新，相邻点间的汉明距离有何关系。

Expand the Path(1900)

题意： 给定n*n网格。你初始处于(1,1)位置，给定字符串初始s只包含D和R字符，分别表示向下和向右移动一个单位。你可以任意选择字符将其在原始位置重复任意多次。对所有结果字符串对应的路径（不能走出网格），求所有能够抵达的网格数。
注意：len(s)在1e5，n在1e8
题解：划分解空间。
如果s中第i个字符前既有D又有R，考察处理完s第i个字符时（所有解中），可能走到的网格点。显然为一个长方形。处理完s第i+1个字符后，该长方形向下或向右平移一个单位，新增范围就是该长方形的长或宽。再注意一些边界条件即s中全是D或R即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;


int main()
{
	int t;scanf("%d",&t);
	for(int i = 0;i<t;i++){
		ll n;cin>>n;	
		string s;cin>>s;
		ll countD = 0,countR = 0;
		char first = s[0];		
		for(int v = 0;v<s.size();v++) if(s[v]=='D') countD++; else countR++;
		if(countD == 0 || countR == 0) cout<<n<<endl; 
		else
		{
			ll ans =  n - (first=='R'?countR:countD) + 1;int v = 0;
			int t1 = countR,t2 = countD;
			v++;
			if(first=='R') countR--;else countD--;
			while(s[v]==first) {v++;ans++;if(first=='R')countR--;else countD--;}
			if(s[v] == 'D') countD--; else countR--;
			ll w = n - t1;   ll h = n - t2;
			ans += w*h;
			ans = ans + h * countR +  w * countD;
			cout << ans << endl;
		}
	}
	system("pause");
	return 0;
}

反思：最初的想法不成熟。只考虑了处理到第一次s出现D和R时能够走到的范围，想当然地认为其能够覆盖所有，并没有考虑再处理后面可能新增的范围。为何要在每个末尾处理，是因为s中初始的D和R必须存在。

Required Length(1700)

题意： 给定两个整数n,x。每次操作选取整数x的某位将x乘以它。问将x变为n位数的最小操作次数。
题解：
实验表明计算结点数不会很多。理论证明：
乘的每一位数分解质因数都是$2,3,5,7$的幂次
因此中间每个结果必可以表示为
$x\cdot 2^a\cdot 3^b\cdot 5^c\cdot 7^d$的形式
由数据范围的限制，中间结果数不会很多。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;


ll dfs(ll x,ll n,map<ll,ll>& m)
{
    auto it = m.find(x);
    if(it!=m.end()) return it->second;
    bool occ[10]; memset(occ,0,sizeof(occ));
    int c = 0;
    ll t = (ll)x;
    while(x > 0)
    {
        occ[x%10]=true; x/=10; c++;
    }

    if((ll)c == n) {m[t]=0;return 0;}
    ll ans = LONG_LONG_MAX;
    for(ll i = 2;i<=9;i++)
    {
        ll a = dfs(t*i,n,m);
        if(occ[i] && a!=LONG_LONG_MAX) 
        ans = min(dfs(t*i,n,m) + 1,ans);
    }
    m[t] = ans;
    return ans;
}


int main()
{
	ll n,x;
    cin >> n >> x;
    map<ll,ll> m;
    ll ans = dfs(x,n,m);
	if(ans == LONG_LONG_MAX) cout << -1 <<endl; else cout << ans <<endl;
    system("pause");
	return 0;
}

反思：走投无路时反思暴力做法是否可行。

Not Adding(1900 GOOD)

题意：给定n个整数组成的数组$a_1,a_2\cdots a_n$.（不同整数）。每次操作选取$i,j$，如果数组中不存在$gcd(a_i,a_j)$则将其加入。问最多可以执行多少次这样的操作。
数据范围：

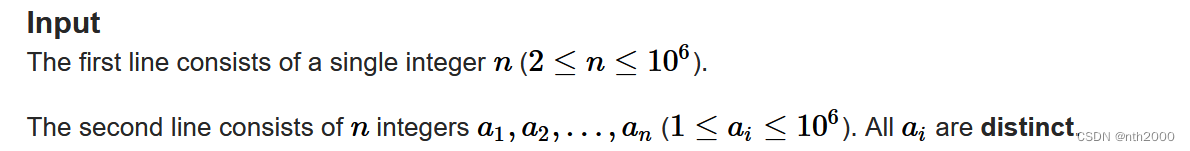
题解：解空间中至多有$1\sim max(a)$种可能。暴力枚举每个数看其是否可以被加入。每个数只可由原数组中是其倍数的数生成，如果这些数的gcd等于该数，则由生成过程该数必须加入。否则一定不能加入（因为这些数的gcd大于该数，后续生成的gcd都大于该数，该数一定不能存在于最终数组）。

#include <bits/stdc++.h>
using namespace std;

#define RG register int
#define LL long long
#define N 200001
typedef long long ll;
ll gcd(ll a,ll b){return b == 0?a:gcd(b,a%b);}
int main()
{
    int n; cin >> n;
    ll a[n]; ll maximal = - 1;set<ll> a_;
    for(int i = 0;i<n;i++){cin>>a[i];maximal = max(maximal,a[i]);}
    bool has[maximal+1]; memset(has,0,sizeof(has));
    for(int i = 0;i<n;i++) {has[a[i]]=true;}
	for(int i = 1;i<=maximal;i++) a_.insert(i);
    for(int i = 0;i<n;i++) {a_.erase(a[i]);}
	vector<ll> r;for(ll v : a_) r.push_back(v);
	ll ans = 0;
	for(ll v:r)
	{
		ll g = 0;
		for(ll s = v;s<=maximal;s+=v) if(has[s]) g=gcd(s,g); 
		if(g==v) ans++;
	}
	cout << ans << endl;
	system("pause");
	return 0;
}

反思：看看数据范围，反思暴力是否可行（考察每一个解是否可以被加入）。