三维天线方向图的空中物联网干扰抑制

考虑三维天线方向图的空中物联网干扰分析与抑 制

孟成俊 ，姆鲁根·A·德什穆赫， ˙Ismail Güvencc，电气与电子工程师协会会士， Arupjyoti Bhuyan ，IEEE高级会员，以及戴怀宇 ，电气与电子工程师协会会士

摘要

由于物联网（IoT）网络的密集部署，干扰管理成为一个关键挑战。随着无人机（UAV）等空中物联网设备的普及，三维环境中的干扰特性将与现有的地面物联网网络有所不同。本文考虑了包含空中和地面链路混合的三维拓扑物联网网络，其中地面节点采用低成本交叉偶极子天线，空中节点则采用全向天线和交叉偶极子天线。在大规模接入通信场景下，我们首先推导出考虑地面节点和空中节点天线辐射图样的物联网接收机信道增益的闭式统计表达式。基于此，计算了遍历可达速率，其为空中接收器高度和累积干扰的高度函数。我们提出了一种低复杂度的干扰抑制方案，该方案利用不同偶极子天线配置下的三维天线辐射图样。结果表明，采用提出的方案后，随着空中接收机高度的增加，遍历可达速率得到提升。此外，我们还表明，最大化峰值速率的地面接收机与空中接收机数量之比随空中物联网接收机高度的增加而增大。

Index Terms— 5G，三维拓扑，天线辐射图样，物联网，无人机，无协调网络。

I. 引言

WITH 随着5G无线网络的出现以及用户对数据需求的持续增长，网络密集化在提升各类5G应用场景下的数据吞吐量方面变得至关重要[2]。在未来的网络中，各种类型的物联网（IoT）设备，如传感器、手机、车辆等，将无处不在并相互连接。因此，大规模接入物联网成为一个不断发展的概念，即无处不在的设备之间相互通信和交互[3]–[5]。为了满足日益增长的物联网需求

稿件收到日期2020年6月8日；修订于2020年10月26日；接受于2020年12月3日。出版日期2020年12月21日；当前版本日期2021年2月12日。本工作部分由美国能源部爱达荷运营办公室合同DEAC07‐05ID14517支持下的INL实验室定向研发（LDRD）计划资助，部分由美国国家科学基金会CNS通过项目编号1 814 727资助。本文的审稿工作由袁超博士协调。（通讯作者：孟成俊。）孟成俊、姆鲁根·A·德什穆赫、 ˙Ismail Güvencc 和戴怀宇均隶属于北卡罗来纳州立大学电气与计算机工程系，美国北卡罗来纳州罗利市，邮编27 606（电子邮件： smaeng@ncsu.edu；madeshmu@ncsu.edu；iguvenc@ncsu.edu； hdai@ncsu.edu）。Arupjyoti Bhuyan 隶属于爱达荷国家实验室无线安全研究所，美国爱达荷州爱达荷福尔斯市，邮编83 402（电子邮件： arupjyoti.bhuyan@inl.gov）。数字对象标识符 1 0.1109/TVT.2020.3046121

设备，已开发并标准化了多种不同的技术。特别是， 3GPP 制定了窄带物联网（NB‐IoT）规范 [6],[7],，而 LoRa 和 Sigfox 被引入作为替代的低功耗广域网（ LPWAN）技术 [8]。

未来的物联网部署预计将涉及各种不同类型的设备和应用。其中，与空中设备（如蜂窝连接的无人机（UAV））的通信最近受到了广泛关注[9],[10]。无人机已被视为三维物联网网络的一部分，用于人群监控目的[11]，而物联网部署的三维场景已在[12],[13]中针对基于RFID的定位进行了研究，[14]则提供了更广泛的三维物联网部署概述。

此类低复杂度物联网网络中的三维通信、传播和干扰场景带来了新的挑战，需要加以解决才能实现有效部署。特别是，在大规模部署低复杂度物联网网络的情况下，干扰管理成为一个关键挑战[15],[16],，据我们所知，该问题在三维空间中尚未得到深入探索。

文献中已研究了三维辐射图样对大规模MIMO波束成形的影响，其中研究了结合波束成形增益的角度相关的天线增益[17]–[21]。无人机的三维波束成形已在[22],[23],中探讨，考虑了三维天线辐射图样与三维空间波束成形的联合效应。然而，这些方法及其相关的干扰缓解方案（如迫零预编码、干扰消除和干扰对齐）可能不适用于解决低成本和低复杂度物联网设备在三维空间中的干扰问题。此类物联网设备通常工作在1 GHz以下，可能仅采用单个（或少量）偶极子天线，并且计算能力有限。尽管已有文献[1],[24]–[26],研究了三维空间中不同配置的偶极子天线辐射图样，但据我们所知，目前尚无关于空中设备干扰特性及缓解方案的详细分析。

在本文中，考虑到空中和地面的物联网节点，我们推导了三维物联网网络中的遍历可达速率，该速率是无人机高度、三维天线辐射图样以及所有物联网发射机累积干扰统计的函数。随后，我们在非协调物联网网络中提出了一种新的干扰抑制方案，该方案利用偶极子天线的三维辐射方向图。我们所提干扰抑制方案的主要思想是，如果我们利用

根据接收机的三维位置，发射端不同的天线辐射图样可以抑制干扰信号并增强期望信号。通常，在二维空间拓扑中，我们假设偶极子天线与 z轴对齐，从而在方位角上产生全向辐射图样。然而，这种偶极子天线设置在典型的低成本物联网设备中虽然常见，但在三维空间（如包含空中节点的网络）中无法实现全向辐射，因为其功率随仰角变化而

变化。另一方面，通过将偶极子天线与不同方向（例如 y轴）对齐，可以获得不同的辐射方向图方向性。

在我们之前的工作[1],中，我们研究了在具有相似设置的三维拓扑网络中利用三维辐射图样进行干扰抑制的方案。具体而言，我们提出了双偶极子和三偶极子天线方案，以根据不同的天线配置生成多种辐射方向图，并通过仿真展示了通过调节空中设备的高度以及空中设备比例所带来的性能提升。另一方面，本文不同于[1],，我们重点在于基于具体的三维拓扑信道模型，从理论上和数值上分析性能提升，并求解遍历可达速率。本文的贡献可总结如下。

– 我们提出了一种基于天线方向图和设备位置的三维拓扑信道模型。我们引入了在二维平面内均匀分布的方位角（φ）和距离（r），以推导物联网发射机与接收机之间三维距离的分布。 – 利用距离和角度的分布，我们推导出包含路径损耗、小尺度衰落和天线增益的信道增益期望的闭式方程。 – 我们推导了在不同偶极子天线设置下空中接收机的遍历可达速率，并提出了相较于传统的单偶极子方案能提升速率的交叉偶极子天线方案。

– 通过数值结果，我们表明所提出的交叉偶极子方案优于单偶极子方案，且随着空中接收器的高度增加，遍历可达速率也随之提高。此外，我们展示了在不同高度的空中接收机情况下，地面接收机与空中接收机的最佳比例。

– 我们引入视距/非视距概率来建模路径损耗，并表明与自由空间路径损耗模型相比，混合视距/非视距路径损耗模型在空中接收机低高度范围内提高了遍历和速率。

本文其余部分组织如下。第二节提供了包含地面和空中物联网节点的物联网系统模型。第三节分析了在考虑单发射机和多发射机场景下，三维天线辐射模式对空地混合物联网网络中物联网链路质量的影响。第四节推导了此类多址物联网网络中的遍历速率，并提出了一种用于干扰抑制的天线选择方案。第五节给出了具有混合地面/空中链路的物联网网络的数值结果，最后一节对全文进行了总结。

符号说明： X ∼U[a, b]表示随机变量 X在 a和 b之间服从均匀分布。 CN(0,1) 表示均值为零、方差为一的复高斯分布。E{X}表示随机变量 X的期望。

II. 系统模型

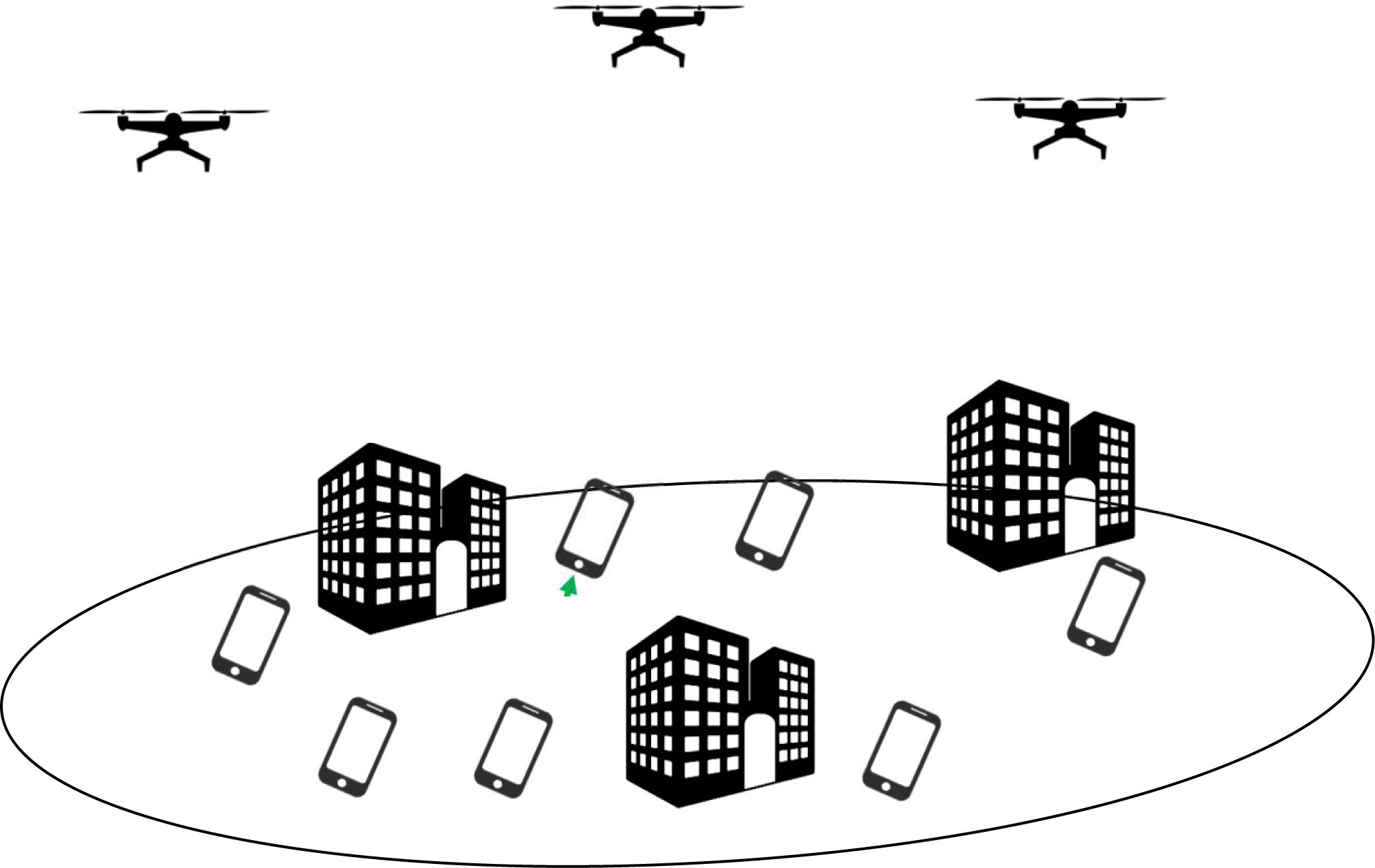
在本研究中，我们考虑如图1所示的包含物联网设备的无协调网络。发射机和接收机对分布在三维空间中，且不受中心基站的资源管理。因此，发射/接收(Tx/Rx)对共享时频资源。根据设备的典型高度，物联网设备被分为地面和空中设备。例如，传感器被视为地面设备，而无人机被视为空中设备。我们假设所有物联网发射机均为地面设备，而物联网接收机可以是地面或空中设备。因此，在同一环境中存在同时进行的地对地(G‐to‐G)和地对空 (G‐to‐A)链路。此类通信拓扑可能具有代表性，例如用于通过远距离物联网链路为无人机提供美国联邦航空管理局远程识别信号[27]，或仅用于无人机从地面节点收集感知数据，同时存在其他共存的地对地物联网通信。

A. 基于3D拓扑的信道模型

发射机和接收机之间的信道通过路径损耗、小尺度衰落和天线增益进行建模。收发机之间的距离可通过两个设备的三维笛卡尔坐标轻松推导得出。设(x Tx i , y Tx i , z Tx i),(x Rx i , y Rx i , z Rx i)表示第 i th 对发射机和接收机的位置。那么，收发机之间的距离计算为d i,i =√(x Tx i − x Rx i) 2 +(y Tx i − y Rx i) 2 +( z Tx i − z Rx i) 2。然后，自由空间路径损耗可表示为

$$
\beta_{i,i} = \left(\frac{4\pi d_{i,i}}{\lambda}\right)^2, \quad (1)
$$

其中 λ是信号的波长。我们将 α表示为小尺度衰落系数， G Tx i 和 G Rx i 分别为发射机和接收机侧的天线增益。

信道系数 gi,i 可以表示为

$$
g_{i,i} = \sqrt{\frac{P G_{Tx_i}}{\beta_{i,i}}} G_{Rx_i} \alpha_{i,i}, \quad (2)
$$

其中 P为发射机的信号功率。小尺度衰落系数的幅度服从瑞利分布，α ∼ CN(0, 1)。尽管由于长距离物联网链路我们考虑非视距小尺度衰落模型，但空对地信道也可用莱斯衰落建模，此时视距分量占主导地位，具体取决于信道环境，如下所示：

$$
g_{i,i} = \sqrt{\frac{P G_{Tx_i}}{\beta_{i,i}}} G_{Rx_i} \left{ \sqrt{\frac{\kappa}{\kappa + 1}} + \sqrt{\frac{1}{\kappa + 1}} \alpha \right},
$$

其中 κ是视距与非视距分量之间的功率比。我们根据第五节‐F部分的仿真结果考虑莱斯衰落信道模型。天线增益 G Tx i 、 G Rx i是发射角(AoD)和到达角(AoA)的函数。该角度可由方位角(φ)和仰角(θ)表示，且函数 G Tx i 、 G Rx i随天线模型的不同而变化。

B. 含视距/非视距概率的路径损耗

地对空链路的视距概率可以通过考虑建筑物遮挡来建模。国际电信联盟（ITU）针对各种不同的标准环境提出了一个概率性地对空视距模型 [28]。特别是，文献[29]中提供了一个适用于无人机的简化概率视距模型，其表达式为：

$$
P_{LoS} = \frac{1}{1 + a_1 \exp(-a_2[90 - \frac{180\theta}{\pi} - a_1])}, \quad (4)
$$

其中参数 a1、 a2由环境决定， θ表示仰角。非视距概率为PNLoS= 1 − PLoS。随后，给定环境中的平均路径损耗计算如下

$$
\beta_{avg} = P_{LoS}(\eta_{LoS}\beta) + P_{NLoS}(\eta_{NLoS}\beta), \quad (5)
$$

其中，ηLoS和 ηNLoS分别表示视距（LoS）和非视距（NLoS）链路的额外路径损耗， β为自由空间路径损耗，如公式(1)所示。注意，对于700兆赫载波频率，(ηLoS , η NLoS) [dB]在城市环境中为(0.6, 17)，在密集城市环境中为(1, 20)，分别对应[30]。

C. 遍历可实现速率

空中接收器的遍历可达速率可以表示为来自连接发射机的信道增益、其他发射机的干扰以及加性噪声的函数，即：

$$
S_i = E\left{\log_2\left(1+ \frac{|g_{i,i}|^2}{\sum_{j \neq i} |g_{i,j}|^2 + \sigma_n^2}\right)\right}, \quad (6)
$$

其中， Si 是空中接收器（ith接收机）的遍历可达速率， σ2 n 是噪声方差。我们可以将式 (6) 中的遍历可达速率近似为

$$
S_i \approx E\left{\log_2\left(1+ \frac{|g_{i,i}|^2}{\sum_{j \neq i} |g_{i,j}|^2}\right)\right} \approx \log_2\left(1+ \frac{E{|g_{i,i}|^2}}{E\left{\sum_{j \neq i} |g_{i,j}|^2\right}}\right), \quad (7)
$$

其中(a)源于在干扰主导的网络中噪声影响可忽略的假设，而(b)则来自与詹森不等式相关的近似[31],[32]。注意，当 |g_{i,i}|^2, |g_{i,j}|^2为非负值时，近似式(b)成立，并且随着随机变量数量的增加，该近似的准确性更高。

III. 天线辐射图样对三维拓扑网络的影响

在本节中，我们研究三维天线辐射方向图对信道增益 |g_{i,i}|^2和可实现速率 S的影响。我们假设地面发射机采用交叉偶极子天线，接收器采用全向天线。我们考虑交叉偶极子天线的配置，该配置将两个偶极子天线部署在正交方向上，其中一个放置在笛卡尔坐标的 z‐轴，另一个放置在 y‐轴。我们考虑一种发射机结构，其能够通过外部天线网络选择两个偶极子天线中的一个，即 z‐轴或 y‐轴。因此，地面发射机能够使用 z‐轴偶极子天线或 y‐轴偶极子天线来发送信号。首先，我们考虑独立的

A. 独立场景分析

1) 与设备位置相关的随机变量的概率密度函数

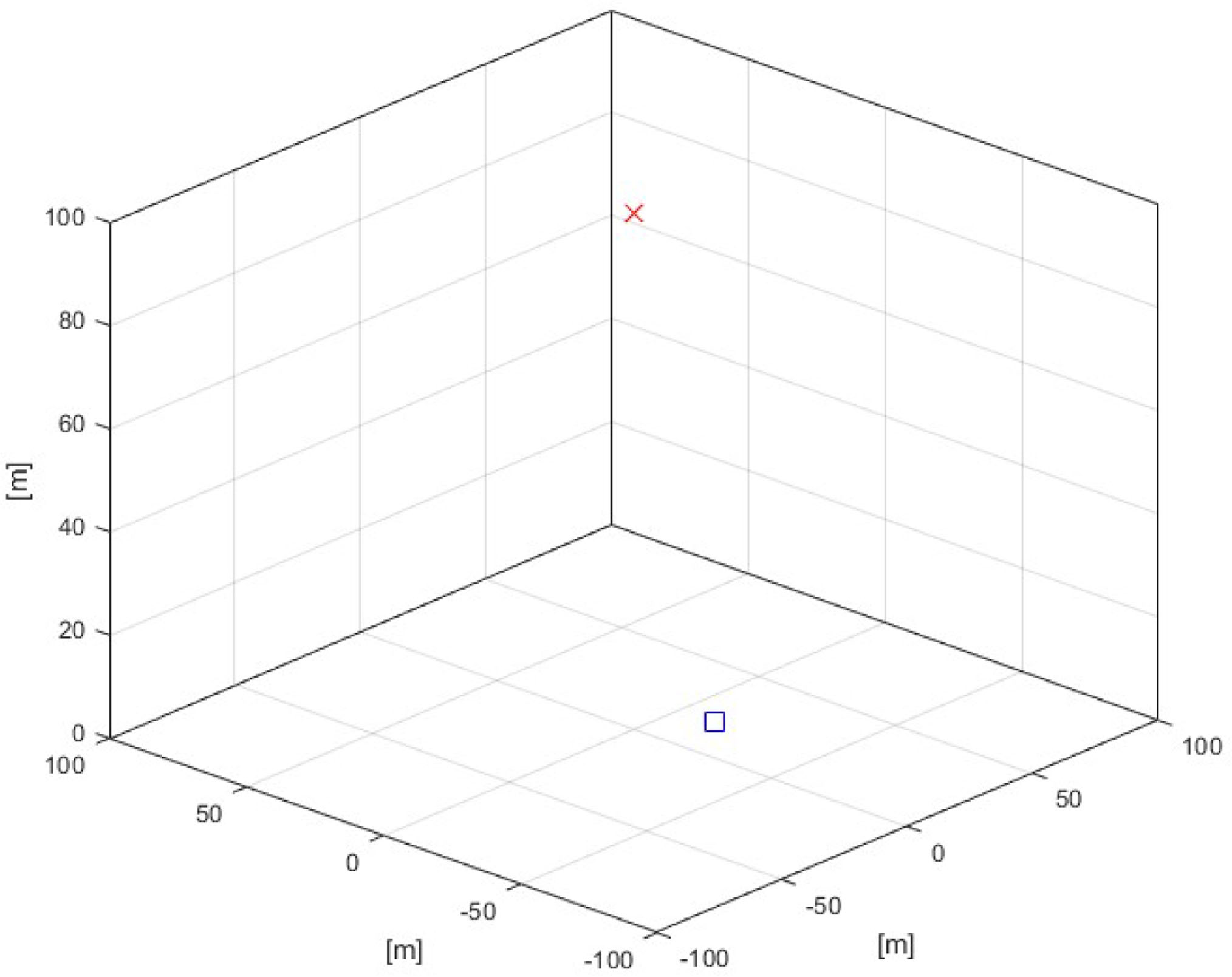
考虑一个收发对。地面发射机的位置由二维圆半径（r）和方位角（φ）决定，空中接收机的位置固定在笛卡尔坐标 （0, 0, h）。物联网网络的三维拓扑示意图如图3所示。随机变量 r、 φ独立且均匀分布

$$
f_r(r) = \frac{1}{m_{max} - m_0}, \quad [m_0 < r < m_{max}],
$$

$$
f_\phi(\phi) = \frac{1}{2\pi}, \quad [0 < \phi < 2\pi], \quad (8)
$$

其中 fr(r), fφ(φ)分别为 r和 φ的概率密度函数（PDF），而 m0、 mmax分别为圆的最小和最大半径。仰角（θ）可表示为 θ= tan−1 ( r h)。然后，随机变量θ的PDF可通过下式推导得出：

$$
d\theta = \frac{h}{r^2 + h^2} dr,
$$

$$
f_\theta(\theta) = \sum f_r(h\tan\theta) \left| \frac{dr}{d\theta} \right| = \sum f_r(h\tan\theta) \left| \frac{h^2 \tan^2 \theta + h^2}{h} \right| = \frac{h}{(m_{max} - m_0)} (\tan^2 \theta + h), \quad [\tan^{-1}(m_0/h) < \theta < \tan^{-1}(m_{max}/h)], \quad (9)
$$

中独立场景下随机变量 θ的概率密度函数。 m0= 10, mmax= 100 h= 100 , .)

其中 (a)来自概率密度函数变换函数。收发机之间的距离可简单表示为 R= h / cosθ。式(9)中 θ的概率密度函数如图4所示，该结果经蒙特卡洛仿真验证。

2) 交叉偶极子天线的天线辐射图样

偶极子天线的辐射方向图通过归一化天线场图样 F来描述。如果我们将偶极子天线放置在 z轴上，则其辐射方向图在方位角（φ）上是全向的。 z轴偶极子天线的归一化天线场图样表示为 [33],[34]：

$$
F_z(\theta) = \frac{\cos(\pi f_0 d_{len} / c \cos\theta) - \cos(\pi f_0 d_{len} / c)}{\sin\theta}, \quad (10)
$$

其中 dlen, c, f0分别表示偶极子天线的长度、光速和载波频率。假设采用半波长偶极子天线（dlen= λ / 2），则 πf0 d len / c = π / 2成立。于是，(10) 可重写为

$$
F_z(\theta) = \frac{\cos(\pi/2 \cos\theta)}{\sin\theta}. \quad (11)
$$

将偶极子天线放置在 y轴上。偶极子天线方向与信号传播方向之间的夹角为cos−1(ˆs · ˆy) = cos−1(sin(θ) sin(φ))，其中ˆs、ˆy分别为信号和 y轴的单位矢量。随后， y轴偶极子天线的归一化天线场图样由下式给出

$$
F_y(\theta, \phi) = \frac{\cos(\pi/2 \cos(\cos^{-1} (\sin\theta \sin\phi)))}{\sin(\cos^{-1}(\sin\theta \sin\phi))}. \quad (12)
$$

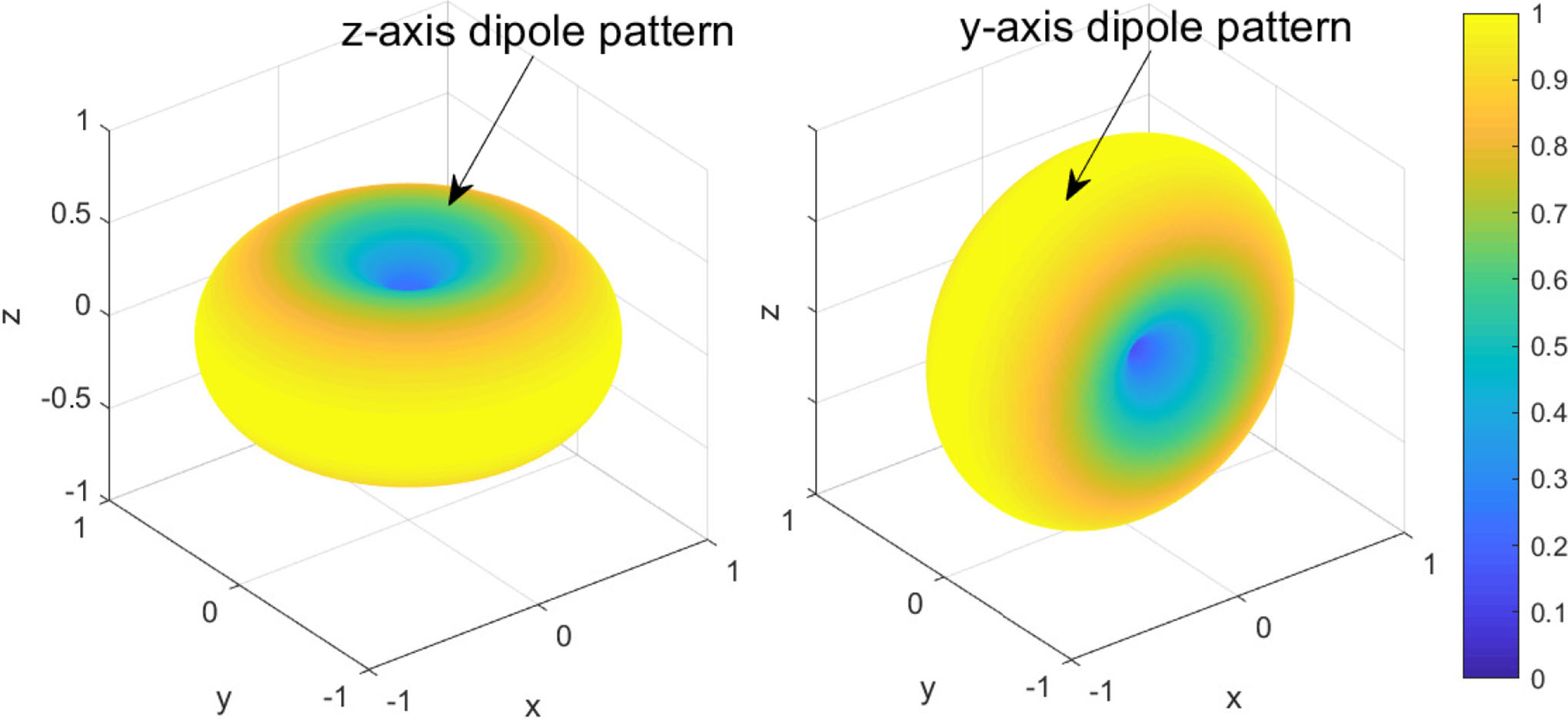
注意， y轴的天线场方向图是方位角（φ）和仰角（θ）的函数。这意味着通过改变方位角和仰角均可改变天线增益。(11) 和 (12) 式分别给出的 z 轴和 y 轴偶极子天线的归一化场方向图如图5所示，坐标系为笛卡尔坐标。

3) 信道增益的期望

为了获得用户或系统的可实现速率，信道增益的统计知识非常重要。因此，我们在此推导信道增益的期望 E{|g_{i,i}|^2 }，以便后续计算遍历可达速率。如果我们考虑地面发射机（G Tx i = F^2_z ）上安装的 z‐轴偶极子天线和一个

空中接收机上的全向天线（GRx i= 1），我们可以将来自 (1)、(2)的信道增益的期望表示如下：

$$
E{|g_{i,i}|^2}_z = E\left{ \frac{P F_z^2}{\beta} \alpha^2 \right} = \frac{P \lambda^2}{16\pi^2} E{\alpha^2} E\left{ \frac{F_z^2}{R^2} \right} = k_1 E\left{ \frac{F_z^2}{R^2} \right}. \quad (13)
$$

由于 α与设备位置无关，（a）成立，且（b）来自 k1= Pλ^2 / (16π^2)。因此，

$$
E{|g_{i,i}|^2} z = k_1 E \left{ \left( \frac{\cos(\pi/2 \cos\theta)}{\sin\theta} \right)^2 \frac{\cos^2 \theta}{h^2} \right} = k_1 \int \left( \frac{\cos(\pi/2 \cos\theta)}{h \sin\theta} \right)^2 \cos^2 \theta f \theta(\theta) d\theta
$$

$$
= \frac{k_1}{(m_{max} - m_0)h} \int_{\tan^{-1}(m_0/h)}^{\tan^{-1}(m_{max}/h)} \left( \frac{\cos(\pi/2 \cos\theta)}{\sin\theta} \right)^2 \cos^2 \theta (1 + \tan^2 \theta) d\theta
$$

$$
= \frac{k_1}{(m_{max} - m_0)h} \int_{\tan^{-1}(m_0/h)}^{\tan^{-1}(m_{max}/h)} \left( \frac{\cos(\pi/2 \cos\theta)}{\sin\theta} \right)^2 d\theta, \quad (14)
$$

其中，(a) 来自期望的定义，(b) 来自公式 (9)，(c) 来自 1+ tan^2 (θ) = sec^2 (θ)。由于 (14) 没有闭式方程，我们利用渐近行为来近似该方程。当空中接收器的高度 (h) 趋于无穷大时，关于 θ 的积分区间趋于 0；tan−1 ( m max / h) → 0，当 h → ∞ 时成立。然后，我们可以在 θ= 0 处应用泰勒级数近似，得到：

$$
E{|g_{i,i}|^2} z \approx \frac{k_1}{(m {max} - m_0) h} \int_{\tan^{-1}(m_0/h)}^{\tan^{-1}(m_{max}/h)} \left( \frac{\pi^2 \theta^2}{16} \right) d\theta = \frac{\pi^2 k_1}{48(m_{max} - m_0) h} \left[ \left{ \tan^{-1} \left( \frac{m_{max}}{h} \right) \right}^3 - \left{ \tan^{-1} \left( \frac{m_0}{h} \right) \right}^3 \right], \quad (15)
$$

其中 （π^2 θ^2 / 16） 是泰勒级数的第一项。

现在，如果我们考虑地面发射机使用 y轴偶极子天线，则可以通过类似方法推导出信道增益：

$$
E{|g_{i,i}|^2} y = k_1 E\left{ \frac{F_y^2}{R^2} \right} = k_1 \int \int \left( \frac{\cos(\pi/2 \cos(\cos^{-1}(\sin\theta \sin\phi)))}{h \sin(\cos^{-1}(\sin\theta \sin\phi))} \right)^2 \cos^2 \theta f \theta(\theta)f_\phi(\phi) d\theta d\phi
$$

$$
= \frac{k_1}{2\pi h (m_{max} - m_0)} \int_0^{2\pi} \int_{\tan^{-1}(m_0/h)}^{\tan^{-1}(m_{max}/h)} \left( \frac{\cos(\pi/2 \cos(\cos^{-1}(\sin\theta \sin\phi)))}{\sin(\cos^{-1}(\sin\theta \sin\phi))} \right)^2 d\theta d\phi, \quad (16)
$$

其中，(a) 来自于期望的定义和 (12)，(b) 来自于 (8) 中的概率密度函数。类似地，由于 (16) 没有闭式方程，如果高度 (h) 趋于无穷大，我们可以在 θ= 0 处应用泰勒级数近似，得到：

$$
E{|g_{i,i}|^2} y \approx \frac{k_1}{2\pi h (m {max} - m_0)} \int_0^{2\pi} \int_{\tan^{-1}(m_0/h)}^{\tan^{-1}(m_{max}/h)} \left(1 - \frac{1}{4}(\pi^2 - 4) \sin^2(\phi) \theta^2 \right) d\theta d\phi
$$

$$
= \frac{k_1}{2\pi h (m_{max} - m_0)} \int_0^{2\pi} \left( \frac{(4 - \pi^2) \sin^2 (\phi) \left[ \left{ \tan^{-1} \left( \frac{m_{max}}{h} \right) \right}^3 - \left{ \tan^{-1} \left( \frac{m_0}{h} \right) \right}^3 \right]}{12} + \tan^{-1} \left( \frac{m_{max}}{h} \right) - \tan^{-1} \left( \frac{m_0}{h} \right) \right) d\phi
$$

$$
= \frac{k_1}{2\pi h (m_{max} - m_0)} \left( \frac{(4\pi - \pi^3) \left[ \left{ \tan^{-1} \left( \frac{m_{max}}{h} \right) \right}^3 - \left{ \tan^{-1} \left( \frac{m_0}{h} \right) \right}^3 \right]}{12} + 2\pi \tan^{-1} \left( \frac{m_{max}}{h} \right) - 2\pi \tan^{-1} \left( \frac{m_0}{h} \right) \right), \quad (17)
$$

其中 (1 − 1/4(π^2 −4) sin^2 (φ)θ^2 )是泰勒级数在 θ= 0处关于固定 φ的第一项和第二项。近似闭式方程(15)、(17)的紧致性在图6中通过仿真展示。可以看出，即使高度(h)较低， (15)也与精确值非常接近；而随着 h的增加，(17)逐渐接近精确值。需要注意的是，由于我们使用了 h → ∞，在较高高度时近似的精度应更高。

、(17)以及m0= 10、 mmax= 100 。)

考虑三维天线方向图的空中物联网干扰分析与抑 制

孟成俊 ，姆鲁根·A·德什穆赫， ˙Ismail Güvencc，电气与电子工程师协会会士， Arupjyoti Bhuyan ，IEEE高级会员，以及戴怀宇 ，电气与电子工程师协会会士

B. 多发射机场景分析

考虑地面上的多个发射机，以及固定在(0, 0, h)笛卡尔坐标处的空中接收器。假设与该空中接收器相连的一个地面发射机使用 z轴偶极子天线或 y轴偶极子天线，而其余所有地面发射机均选择 z轴偶极子天线。我们比较根据与之连接的地面发射机所选择的偶极子天线类型，空中接收器的可实现速率 S的变化情况。如前所述，地面发射机配备有交叉偶极子天线，能够选择 z轴或 y轴偶极子天线。

直观上，从天线场方向图可以看出， z轴偶极子对地面接收器具有更高的天线增益，而 y轴偶极子天线对空中接收器表现出更优的性能。

考虑地面发射机与空中接收器连接时采用 z‐偶极子天线的情况。此时，E{|g_{i,i}|^2}等于(15)中的E{|g_{i,i}|^2} z。由于其他发射机采用 z‐偶极子天线，E{|g {i,j}|^2}也等于E {|g_{i,i}|^2} z。假设收发对数量为 K，并将(15)中的E{|g {i,i}|^2}_z代入 ζz，则可写出空中接收器的遍历可达速率，如(7)所示。

$$
{S_i}_z \approx \log_2\left(1+ \frac{\zeta_z}{(K -1)\zeta_z}\right) = \log_2\left(1+ \frac{1}{K -1}\right). \quad (18)
$$

需要注意的是，采用 z‐偶极子天线的遍历可达速率仅取决于网络中通信对的数量（K）。其原因是期望信号和干扰信号具有相同的统计值。

接下来，我们考虑地面发射机采用 y‐偶极子天线的情况。此时，期望信号的信道增益E{|g_{i,i}|^2 }等于(17)中的 E{|g|^2}_y 。然后，将E{|g|^2}_y 代入 ζ y 后，空中接收器的遍历可达速率可以表示为

$$
{S_i}_y \approx \log_2\left( 1+ \frac{\zeta_y(h)}{(K -1)\zeta_z(h)} \right), \quad (19)
$$

其中信道增益 ζ_y(h) 和 ζ_z(h)是高度的函数(h)。我们有趣地观察到遍历可达速率由(19)可知，随着高度增加其值提升，而由(18)得到的遍历可达速率作为高度的函数保持不变，第五节的仿真结果展示了这一点。这意味着我们可以根据设备类型采用不同的天线辐射图样来改善可实现速率的性能。例如，可以设置与地面接收机相连的地面发射机选择z轴偶极子天线，与空中接收器相连的发射机选择 y轴偶极子天线。此外，随着空中接收器的高度增加，可以获得更好的性能。

IV. 多个发射/接收对场景的分析

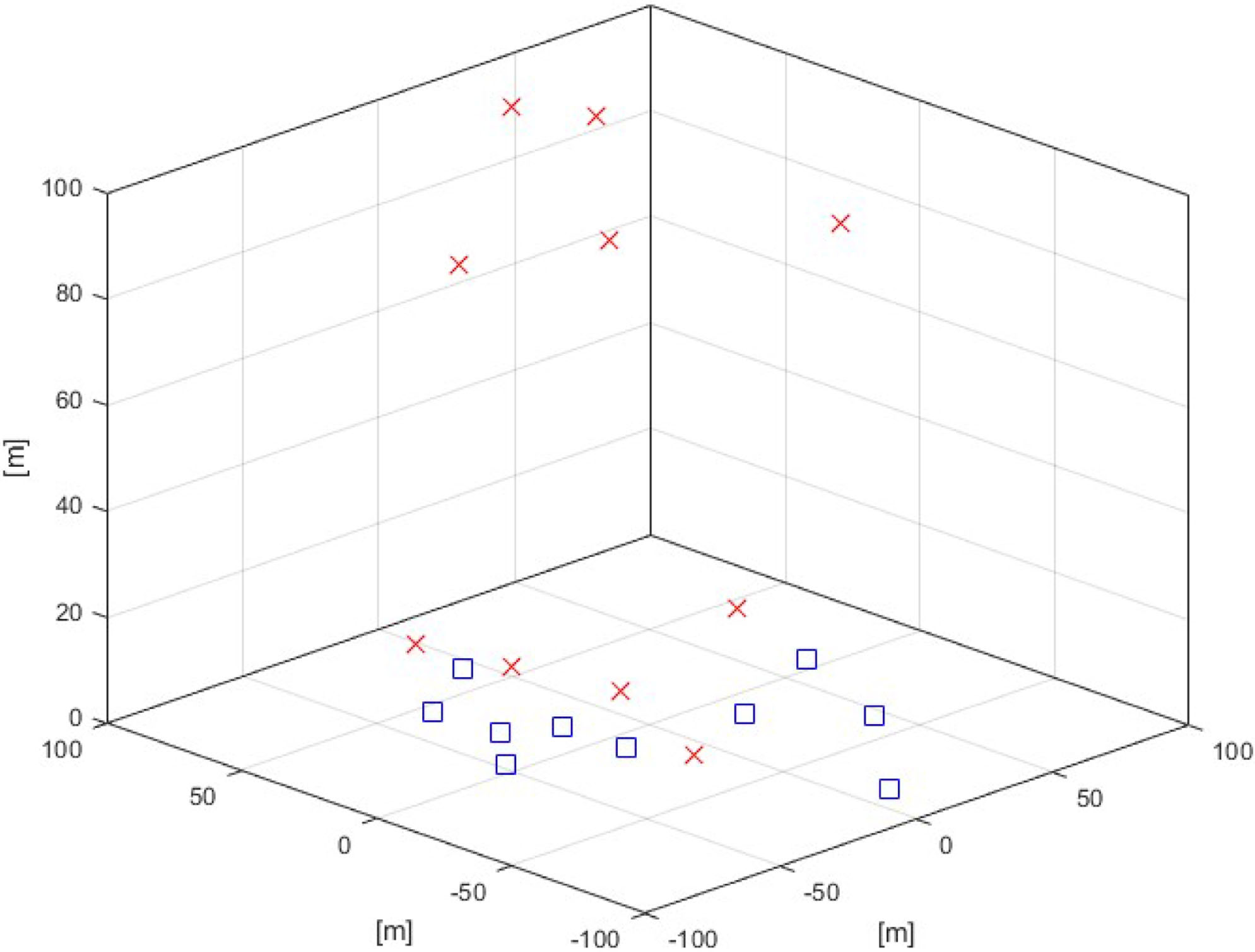
在本节中，我们将场景扩展到多收发对，且不再限制接收器的位置。这意味着接收器不再固定于(0,0, h)笛卡尔坐标，而是由随机变量决定。此外，接收器可以是地面接收器或空中接收器。我们假设所有空中接收机的高度均固定为 h。图7展示了物联网网络中多收发对场景下三维拓扑设计的新示意图。

A. 与节点位置相关的随机变量的概率密度函数

首先，各个发射机和接收机的位置由独立生成的随机变量决定。表示设备位置的均匀分布随机变量的概率密度函数由下式给出

$$
f_{r_{Tx}}(r_{Tx}) = \frac{1}{m_{max} - m_0}, \quad [m_0 < r_{Tx} < m_{max}],
$$

$$
f_{r_{Rx}}(r_{Rx}) = \frac{1}{m_{max} - m_0}, \quad [m_0 < r_{Rx} < m_{max}],
$$

$$
f_{\phi_{Tx}}(\phi_{Tx}) = \frac{1}{2\pi}, \quad [0 < \phi_{Tx} < 2\pi],
$$

$$
f_{\phi_{Rx}}(\phi_{Rx}) = \frac{1}{2\pi}, \quad [0 < \phi_{Rx} < 2\pi], \quad (20)
$$

其中，rTx和 rRx是发射机和接收机的二维圆半径， φTx和 φRx是发射机和接收机的方位角。由于发射机和接收机的位置由随机变量决定，因此需要计算发射机/接收机随机变量之间的相对差异，以推导出发射机与接收机之间的距离（R）：

$$
\hat{\phi} = |\phi_{Rx} - \phi_{Tx}|, \quad \hat{r} = \sqrt{(r_{Tx})^2 + (r_{Rx})^2 - 2 r_{Tx} r_{Rx} \cos \hat{\phi}}, \quad (21)
$$

其中 φ是发射机和接收机之间方位角的相对差值，ˆr是二维地面平面上收发机之间的距离。ˆr的方程来源于三角学中的余弦定理。ˆ φ的概率密度函数可以表示为

$$
f_{\hat{\phi}}(\hat{\phi}) = \frac{1}{2\pi^2}(2\pi - \hat{\phi}), \quad [0 < \hat{\phi} < 2\pi], \quad (22)
$$

其中，(22) 是根据两个独立随机变量之和的概率密度函数等于这两个随机变量概率密度函数的卷积这一性质推导得出。ˆ r 的概率密度函数的闭式方程难以获得。作为替代方法，我们使用 MATLAB 中的概率密度函数拟合工具获得该概率密度函数的近似形式。通过仿真结果，我们观察到 ˆr 的概率密度函数与瑞利分布非常接近：

$$
f_{\hat{r}}(\hat{r}) \approx \frac{\hat{r}}{b^2} e^{-\hat{r}^2 / (2b^2)}, \quad (23)
$$

其中，拟合概率密度函数中的系数 b= 60.7994，当 m0=10时，m_max = 100。然后，我们可以从方程ˆr= h tan(θ)推导出 θ的概率密度函数如下：

$$
f_\theta(\theta) = \sum f_{\hat{r}}(h \tan\theta) \left| \frac{d\hat{r}}{d\theta} \right| = \sum f_{\hat{r}}(h \tan\theta) \left| \frac{h^2 \tan^2 \theta + h^2}{h} \right| = \frac{h^2 \tan\theta}{b^2} e^{-h^2 \tan^2 \theta / (2b^2)} \sec^2 \theta, \quad [0 < \theta < \tan^{-1}(2m_{max}/h)]. \quad (24)
$$

ˆ φ的概率密度函数的闭式方程、ˆr和 θ在图8中进行了仿真，并与蒙特卡洛仿真进行了比较。在图8(b)中，可以观察到基于瑞利分布（红色实线）的ˆr的分析PDF与精确分布（蓝色直方图）非常吻合。

、(23)、(24)中多发射机/接收机场景下随机变量的概率密度函数，其中 m0= 10、 mmax= 100、 h= 100。(a) ˆφ的概率密度函数。(b) ˆr的概率密度函数。(c) θ的概率密度函数。)

B. 信道增益的期望

信道增益的期望可以通过随机变量的新概率密度函数计算。通过对独立场景进行类似的分析，可以得到地面发射机配备 z轴偶极子天线和地面发射机配备 y轴偶极子天线情况下的信道增益的期望，如下所示：

$$
E{|g_{i,i}|^2}_z \approx -\frac{3\pi^2 k_1 e^{-3k_2/8}}{512 b^2 k_2} \left( \sqrt{6\pi k_2} \text{erfi}\left( \frac{\sqrt{k_2}(4\theta^2 + 3)}{2\sqrt{6}} \right) - 4 e^{k_2(4\theta^2 + 3)/24} \right) \Bigg|_0^{\tan^{-1}(2\tilde{m}/h)} = \zeta_z, \quad (25)
$$

$$
E{|g_{i,i}|^2} y \approx \left( -\frac{3k_1 e^{-3k_2/8}}{64\pi^2 b^2 k_2} \right) \left( \frac{5\pi^2}{3} - \frac{\pi^4}{4} \right) \left( \sqrt{6\pi k_2} \text{erfi}\left( \frac{\sqrt{k_2}(4\theta^2 + 3)}{2\sqrt{6}} \right) - 4 e^{k_2(4\theta^2 + 3)/24} \right) \Bigg|_0^{\tan^{-1}(2m {max}/h)}
$$

$$
+ \left( \frac{k_1 e^{-3k_2/8}}{4b^2 \sqrt{k_2}} \right) \left( \frac{\sqrt{3\pi}}{2} \text{erfi}\left( \frac{\sqrt{k_2}(4\theta^2 + 3)}{2\sqrt{6}} \right) \right) \Bigg| 0^{\tan^{-1}(2m {max}/h)} = \zeta_y, \quad (26)
$$

其中erfi()是虚误差函数。(25)和(26)的证明见附录。近似式(25)和(26)的精度如图9所示。与图6中的独立场景相比，我们观察到类似的行为。闭式方程与精确值接近，并且随着 h的增大，近似精度提高。

在上述分析中，我们假设接收天线为全向的，G_{Rx_i} = 1。然而，我们也可以考虑物联网的这种情况

、(26)中的多收发对场景下，不同偶极子天线布置时信道增益的期望随高度(h)的变化。m0= 10, mmax= 100 。)

接收机也配备交叉偶极子天线。为了获得接收机天线增益，我们可以类似地采用在交叉偶极子天线发射机设置中的研究结果。地面物联网接收机使用 z轴偶极子天线，而空中物联网接收机则根据每种天线配置的方向性选择 y轴偶极子天线。在这些情况下，接收机采用与发射机偶极子天线相同方向的偶极子天线（例如，发射机和接收机均使用 z轴偶极子天线和 y轴偶极子天线）。随后，相同方向偶极子天线的信道增益期望可表示如下：

$$
E{|g_{i,i}|^2}_{z,z} = k_1 E\left{ \frac{F_z^4}{R^2} \right}, \quad (27)
$$

$$
E{|g_{i,i}|^2}_{y,y} = k_1 E\left{ \frac{F_y^4}{R^2} \right}. \quad (28)
$$

我们通过数值仿真在图14中展示了交叉偶极接收机天线的预期增益。

C. 视距/非视距概率的影响

在上一节中，我们考虑了自由空间路径损耗模型，以推导关于信道增益的期望的闭式方程。在本节中，我们采用式(5)中的混合路径损耗模型，以观察视距概率对系统的影响。包含视距概率影响的信道增益的期望可表示如下，适用于配备z轴偶极子天线的地面发射机：

$$
E{|g_{i,i}|^2} z = E\left{ \frac{P F_z^2}{\beta {avg}} \alpha^2 \right} = \frac{k_1}{\eta_{NLoS}} E\left{ \frac{F_z^2}{R^2} \left( \frac{1 + a_1 \exp(-a_2[90 - 180\theta/\pi - a_1])}{\eta_{LoS}/\eta_{NLoS} + a_1 \exp(-a_2[90 - 180\theta/\pi - a_1])} \right) \right} \quad (29)
$$

而对于采用 y轴偶极子天线的地面发射机，其信道增益的期望计算如下：

$$
E{|g_{i,i}|^2} y = \frac{k_1}{\eta {NLoS}} E\left{ \frac{F_y^2}{R^2} \left( \frac{1 + a_1 \exp(-a_2[90 - 180\theta/\pi - a_1])}{\eta_{LoS}/\eta_{NLoS} + a_1 \exp(-a_2[90 - 180\theta/\pi - a_1])} \right) \right}. \quad (30)
$$

图10显示，在路径损耗模型中，视距概率在低高度范围内对不同偶极子天线设置下的干扰抑制具有积极作用。可以观察到，在密集城市模型中，相比于自由空间模型，低高度下 z轴和 y轴偶极子天线之间的功率电平差更大，这将减少来自z轴偶极子天线发射机的干扰。

D. 提出的方案

我们提出一种天线选择策略，其中与地面接收器相连的地面发射机使用 z轴偶极子天线，而与空中接收机相连的地面发射机使用 y轴偶极子天线。在实际中，发射机需要解码来自接收器的消息或接收前导码，以判断接收器类型是地面还是空中。一种可行的天线选择方法是通过测量前导码的接收信号功率来决定。具体而言，选择 z轴偶极子天线时，来自地面接收器的接收信号功率更高；而选择 y轴偶极子天线时，来自空中接收机的接收信号功率更高。

设 G={F^2_z , F^2_y }为候选天线选择，其中F^2_z , F^2_y分别为 (11)、(12)中的 z轴和 y轴偶极子天线的天线增益。由于我们考虑的是交叉偶极子配置，无论是 z轴偶极子天线还是 y轴偶极子天线，其基数 |G| 均为2。随后，根据最高的接收前导信号功率做出天线选择决策。

$$
{G_{Tx_i}} = \arg \max_{\forall G_{Tx_i} \in G} P G_{Tx_i} / (\beta_{i,i}) \alpha^2_{i,i} \sigma^2_s, \quad (31)
$$

其中 σ^2_s是前导信号的信号功率。我们在第V‐D节中验证了该天线选择方法与发射机完全知晓接收机为空中或地面接收器的情况相比，能够获得非常相似的性能。

空中接收器（ith接收机）的遍历可实现速率可根据(7)表示为

$$
S_i \approx \log_2\left(1+ \frac{E{|g_{i,i}|^2}}{E\left{\sum_{j \neq i} |g_{i,j}|^2\right}}\right) = \log_2\left(1+ \frac{\zeta_y}{(K_{grd})\zeta_z + (K_{arl}-1)\zeta_y}\right), \quad (32)
$$

其中 ζz、 ζy来自(25)和(26)， Kgrd、 Karl分别为与地面接收机和空中接收器相连的地面发射机数量； Kgrd+ Karl= K。

V. 数值结果

在本节中，我们展示了所提出的方案在遍历可达速率和和速率性能方面的仿真结果。仿真设置如表I所示。我们假设发射机完全知晓接收器的类型（地面或空中设备）。

A. 单空中接收机的遍历可达速率

在图11中，我们展示了第三节‐B场景下空中接收器的遍历可达速率以及期望信号和干扰信号功率。在该场景中，单个空中接收器固定在(0, 0, h) m处。在图11(a)中， z‐轴偶极子天线的闭式方程（红色虚线）来自(18)， y‐轴偶极子天线的闭式方程（蓝色虚线）来自(19)。蒙特卡洛结果是通过(6)中的精确遍历可达速率直接仿真得到的。因此，闭式解与蒙特卡洛结果之间的差距来源于(7)中的近似过程。可以观察到，在来自地面发射机的 y‐轴偶极子设置下，随着空中接收器高度的增加，速率逐渐上升（蓝线），而在来自地面发射机的 z‐轴偶极子设置下，速率保持不变（红线）。

遍历可达速率。(b) 期望信号和干扰信号功率。)

图11(b)中的仿真结果与图11(a)一致，表明y轴偶极子天线（蓝色曲线）的期望信号功率与干扰信号功率（绿色曲线）之间的差距持续增大，而 z轴偶极子天线（红色曲线）的期望信号功率与干扰信号功率（绿色曲线）之间的差距保持不变。需要注意的是，我们仅给出了 z轴偶极子天线设置下的干扰信号功率结果，因为 z轴偶极子和 y轴偶极子的干扰信号功率相同。从仿真结果可以看出，根据接收机类型（地面/空中）的不同辐射方向图可以改善系统性能。此外，我们还表明，随着空中接收器的高度增加，性能变得更好。

B. 具有多个发射/接收对的空中接收机的遍历可达速率

第四节场景中的遍历可达速率如图12所示。在该场景中，所有地面/空中设备

随机分布在给定空间中。与地面接收器相连的发射机采用 z轴偶极子天线，与空中接收器相连的发射机采用 y轴偶极子天线。收发对（K）的数量为10。闭式方程的仿真结果来自公式(32)，对应不同数量的空中接收机（Karl）。我们观察到，随着空中接收器的高度增加，可实现速率的性能提高；而随着空中接收机数量的增加，性能下降。这意味着，随着空中接收机数量的增加，使用 y轴偶极子天线的发射机数量也成比例增加，从而导致指向各个空中接收机的干扰信号功率增加，进而降低了性能。作为参考，我们还给出了所有发射机均采用 z轴偶极子天线时的仿真结果（红色曲线），其性能较差且曲线平坦。

C. 具有多个发射/接收对的空中接收机的遍历和速率

在图13中，我们通过蒙特卡洛仿真描绘了第四节场景中的遍历和速率。发射/接收对的数量为10（K= 10），遍历和速率由S_sum=∑_{i=1}^K S_i给出。在此仿真中，我们固定发射/接收对的数量，同时增加空中接收机的数量（Karl）。例如， K_arl = 1表示网络中10%为空中接收器，而 K_arl = 5表示网络中50%为空中接收器。观察发现，根据空中接收器的高度，地面接收机与空中接收机之间的最佳比例有所不同。在较低高度（h= 50 m）情况下，网络中50%的空中接收机（Karl = 5）达到最佳速率（黑色圆圈线），而网络中10%的空中接收机（Karl = 1）达到最差速率（蓝色方块线）。另一方面，在中等高度（h= 150 m）情况下，网络中30%的空中接收机达到最佳速率（青色菱形线），而70%的空中接收机达到最差速率（紫色加号线）。此外，在较高高度（h= 400 m）的情况下，网络中10%的空中接收机达到最佳速率（蓝色方块线），而70%的空中接收机达到最差速率（紫色加号线）。需要注意的是，指向空中接收机的 y轴偶极子天线不仅提高了空中接收器的可实现速率，也提高了地面接收器的可实现速率，从而在两种情况下均减少了干扰。

遍历和速率随网络中空中接收机的百分比在不同高度下的变化如图14所示。我们可以观察到，峰值速率对应的空中接收器百分比因高度不同而有所差异。在空中接收机的低/中/高高度情况下，50%/30%/10%的空中接收器比例分别达到峰值。请注意，该观察结果与图13中讨论的结果一致。我们得出结论：网络中地面/空中接收器的最佳比例受空中接收机高度的影响。在低高度时，50%的空中节点可能是最优的，而在高高度时，单个空中接收器可能达到最佳性能。此外，我们对比了所提出的交叉偶极天线

方案（蓝色曲线）与发射机仅使用z轴偶极子天线的方案（红色曲线）相比。我们观察到，提出的方案在所有高度上均实现了更好的性能。

在图14中，我们还比较了全向（蓝色曲线）和交叉偶极（黑色曲线）接收天线模型之间的性能差异。需要注意的是，本文通常假设接收机采用全向天线，以便观察发射端不同偶极子天线方向图的影响。仅在图14中，我们对交叉偶极天线接收机也采用了类似的天线选择方法，即地面接收器使用z轴偶极子天线，空中接收器使用 y轴偶极子天线。我们观察到接收天线方向性带来的额外天线增益，尤其是在低高度时更为明显。

D. 基于接收功率测量的天线选择

在之前的仿真结果中，我们假设发射机知道接收机的类型（即空中或地面），并直接选择z轴或 y轴偶极子天线。在本节中，我们采用式(31)中的策略，通过测量信号功率来选择天线。在图15中，我们比较了基于完美信道知识和基于测量的天线选择策略的遍历和速率。可以看出，两种策略的性能接近，这意味着与完美已知接收机情况相比，基于信号功率的天线选择性能损失可以忽略不计。

E. 采用混合视距/非视距路径损耗模型的性能

图16显示了在不同空中接收机高度下，基于(5)式中的混合视距/非视距路径损耗模型的遍历和速率。遍历和速率是根据(29)、(30)式计算得出的。可以观察到，在城市和密集城市环境中，低高度情况下的性能相比自由空间路径损耗模型的结果（图14）有所提升。该观察结果与图10中的结果一致，其中

在低高度时， z轴偶极子天线的信道增益显著降低。

F. 莱斯衰落信道模型下的性能

在图17中，我们通过遍历和速率展示了莱斯衰落信道模型 (3)中的性能。我们观察到，遍历和速率的趋势与瑞利衰落信道相似。

中遍历和速率随网络中空中接收机的百分比的变化，其中 K因子为= 10 dB。)

模型见(2)。需要注意的是，由于瑞利衰落和莱斯衰落模型的小尺度衰落系数的期望值相同，因此遍历可达速率的解析近似结果也相同；E{α^2}= E{ κ/(κ+1) + 1/(κ+1) α^2}= 1。

VI. 结论

本文提出并分析了一种利用辐射方向图分集特性的干扰抑制方案，该方案适用于具有低复杂度无线射频的非协调空中/地面物联网网络。我们提出在发射机处采用交叉偶极子天线配置，根据接收机类型选择使用 z轴偶极子天线或 y轴偶极子天线。我们分析了考虑偶极子天线三维辐射图样和物联网设备位置的三维拓扑信道模型，并从理论上证明 y轴偶极子天线对空中接收机的性能优于 z轴偶极子天线。通过仿真结果观察到，与仅使用 z偶极子天线的方案相比，交叉偶极子天线方案表现出更优的性能，并且通过增加空中接收机的高度可以进一步提升性能。此外，根据空中接收机的高度（低、中、高），地面接收机与空中接收机的最佳比例有所不同，本文在多种传播场景下对此进行了研究。本文重点研究交叉偶极子天线配置对物联网发射机的影响，因此假设接收机配备的是全向天线辐射方向图。该场景的一种扩展是物联网接收机也配备交叉偶极子天线。结果表明，所提出的方案通过接收机天线方向图在低空范围获得了额外增益。