纽结及其不变量解析

纽结及其不变量

一、引言

纽结已经存在了很长时间。纽结的起源可以追溯到远古时代，当时出现了通过打结来记录事物的方式。我们在日常生活中也能看到纽结。例如，当我们系鞋带或打领带时，实际上就是在打纽结。

从学术上讲，纽结也具有重要意义。自上个世纪以来，纽结理论已发展成为拓扑学的一个重要分支。拓扑学是一门研究几何图形连续变形的学科。而纽结理论以纽结和链环为研究对象，主要讨论它们在连续变形下保持不变的特性。[1,2,3]

纽结理论的研究起源于英国物理学家开尔文勋爵于1867年提出的一个原子模型。他认为原子是以太（Ether，当时充满宇宙的一种介质）中打结的涡旋，不同的纽结代表不同的化学元素。根据他的设想，如果能对这些纽结进行分类，就有可能绘制出化学元素的周期表。这一理论曾促使一批物理学家研究绳索和环圈打结的现象。尤其值得一提的是，一位名叫泰特的英国人与其他学者花费了20年时间对纽结进行分类，并编制了第一张纽结表。

现在人们知道，这一理论是错了。元素周期表是由门捷列夫发现的。尽管最初的问题当时并未解决，但纽结激发了数学家们的极大兴趣，数学家们开始研究纽结。

纽结理论的基本主题或核心主题是纽结的分类，即如何区分两个结或证明它们是相同的。这已被列为上个世纪未解决的数学问题之一。解决方法是寻找能够区分它们的不变量。

本文主要讨论纽结及其不变量，内容包括以下几个部分：

• 纽结概念的解释：由于本文主要讨论纽结及其不变量，预先理解纽结的概念非常重要。
• 纽结的几种不变量：在学习了基本概念之后，我们将讨论几种可用于区分不同类型纽结的纽结不变量。
• 莫尔斯函数简介：莫尔斯函数也与纽结不变量相关。不同类型的纽结具有不同的莫尔斯函数。
• 纽结的亏格的性质：本部分将涵盖欧拉示性数和塞弗特曲面。

II. 正文

A. 预备知识

本文的主要研究对象是纽结，其定义如下。

定义 1。 纽结是嵌入在 $ \mathbb{R}^3 $ 内的一个嵌入圆 $ S^1 $。

在定义中，纽结存在于三维空间中，这使得我们难以直观地观察和研究它们。为了更好地描述纽结，我们希望将其投影到一个平面上，形成纽结的图示。

定义 2. 纽结图 是一个平面上的浸入曲线，且在每个交叉点处标有哪一根线在上方、哪一根线在下方的信息。

有许多看似不同的纽结具有完全相同的拓扑性质。因此，为了更好地研究这些纽结的拓扑性质，我们作出如下定义。

定义 3. 等价的两个纽结如果其中一个可以通过不产生自交的形变变为另一个，则称这两个纽结是等价的。

同一个（等价的）纽结可以有许多不同的图示。因此，研究两个给定的图示是否表示同一个（等价的）纽结是一个很自然的问题。这个问题已经得到了完全的回答，如下所述。

定理 4 (雷德梅斯特) 两个纽结图表示等价纽结当且仅当它们通过有限次同痕和以下三种类型的R-移动相关联：

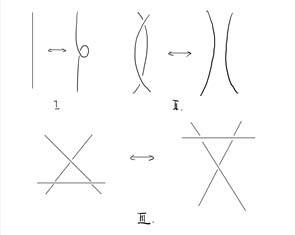
例如，平凡结和三叶结是两种不同类型的纽结，因为它们无法通过上述三种类型的R‐移动变形为相同的纽结。

B. 纽结不变量

定义 5. 纽结不变量是为每个纽结定义的一个量，并且该量在一类等价纽结中保持不变。

根据定义，我们使用纽结不变量来确定两个结是否等价。

C. 三色性

你可以思考如何判断平凡结与三叶结是否等价。解决这个问题的一种方法是使用三色性。首先，我们需要了解一个与三色性相关的重要概念——三色性。

定义 6。 三色性是指纽结根据特定规则用三种颜色着色的能力。

你可能对定义中的“某些规则”感到困惑。以下是三色性的两条特定规则。

定理7. 三色性规则
如果纽结图的每条strand都可以被染成三种颜色之一，并满足以下两条规则，则该纽结是三色可染的：

1. 至少使用两种颜色
2. 在每个交叉点处，strands 的颜色要么完全相同，要么完全不同。

以下是三色可染的纽结和非三色可染的纽结的例子。

对于三色可染的纽结，如图3所示，每个交叉点都被染成三种不同的颜色（红色、蓝色和绿色）。

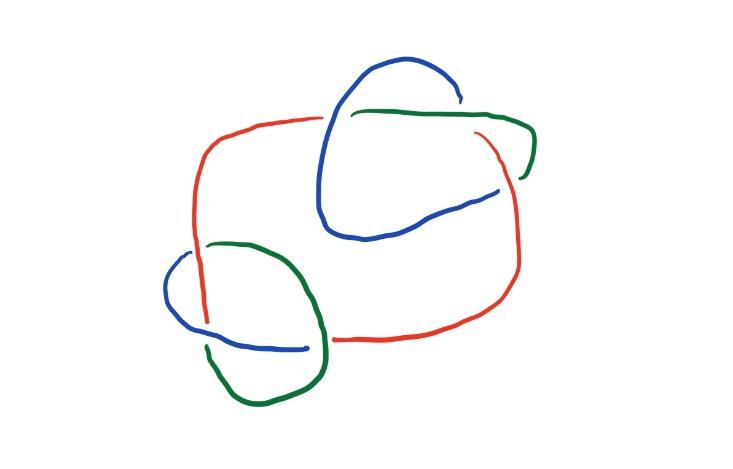
对于非三色可染的纽结，如图4所示，中间的交叉点无法进行三色染色。

定理. 三色性是一种纽结不变量。

证明。 为了证明三色性是纽结的不变量，只需说明三色性在定理4中的三种雷德梅斯特变换R1、R2和R3下保持不变即可。

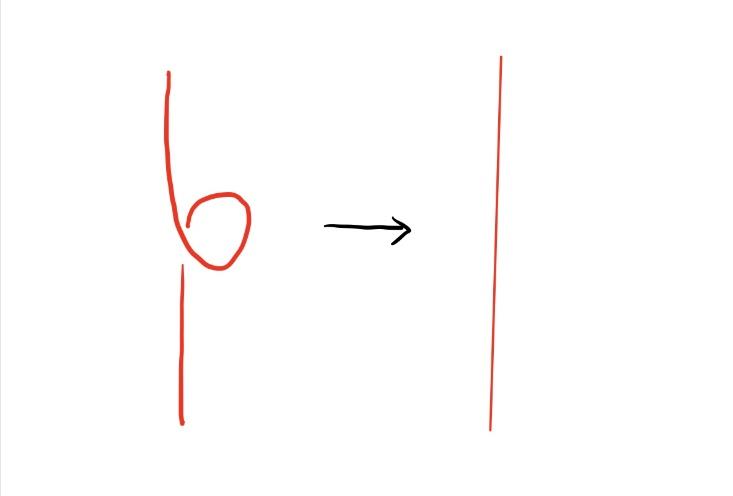
我们首先证明在进行 $ R_1 $ 操作时三色性保持不变。假设 $ D $ 是一个纽结 $ K $ 的图示，而 $ D’ $ 是由 $ D $ 经过一次R1移动得到的图示。进一步假设 $ D $ 具有三色性。我们要证明 $ D’ $ 也具有三色性。

如图5所示，R1移动只涉及纽结的一条strand。我们可以合理地假设这条strand被染成红色。由于在R1移动之后，仍然只有一条strand，因此我们可以继续将其染成红色，而 $ D’ $ 的其他strand与 $ D $ 的颜色相同。容易验证我们得到了 $ D’ $ 的一个三色性，因此证明完成。

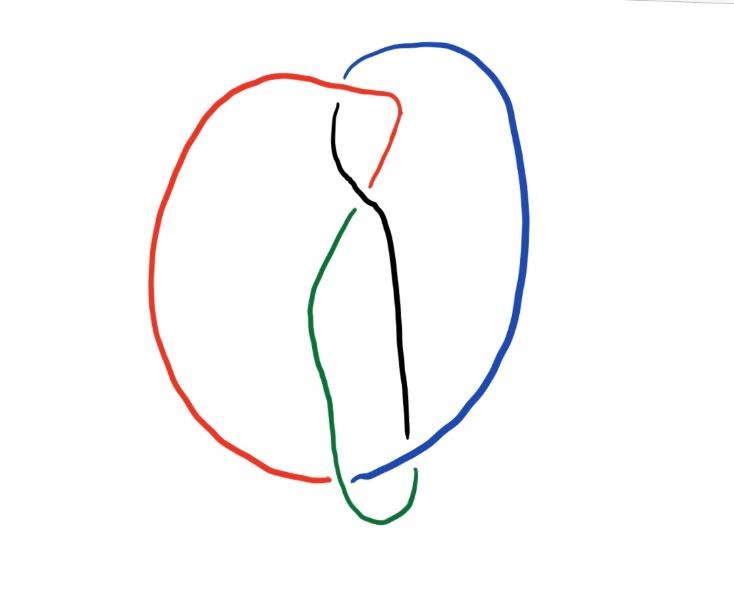
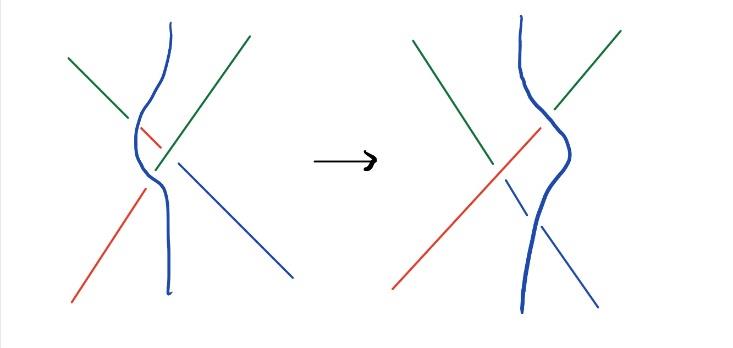
如图6所示，在R2移动中涉及纽结的两个strand。我们可以假设一个strand为红色，另一个strand为蓝色。在进行R2移动后，我们能够在每个交叉点处拥有三种不同的颜色（红色、蓝色和绿色）。因此，R2移动不会改变纽结的三色性。

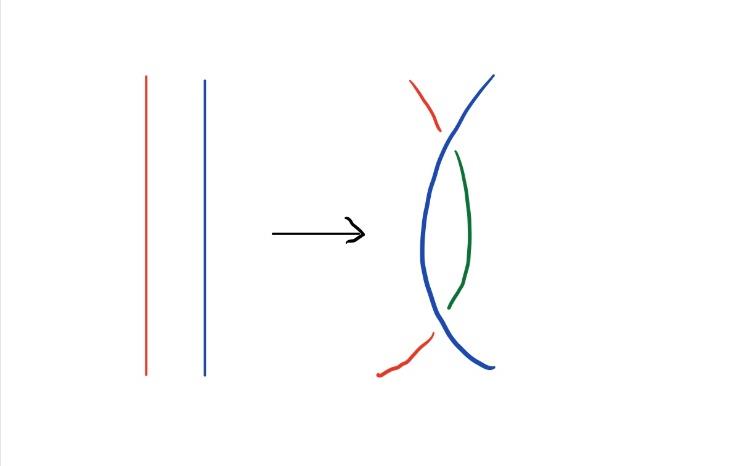
如图7所示，R3变换涉及纽结的三个strands。在每个交叉点处，都用三种不同的颜色着色。在进行R3变换后，有两个交叉点用三种不同颜色着色，一个交叉点用单一颜色着色。因此，R3变换不改变纽结的三色性。

例如，平凡结不具有三色性，因为它不满足至少使用两种颜色的要求。然而，三叶结具有三色性。因此，通过使用三色性，我们可以证明平凡结和三叶结不是同一种纽结。

D. 莫尔斯函数

为了构造更多的纽结不变量，我们将在本部分重点关注莫尔斯函数。

定义 9. 一个函数 $ f: \mathbb{R} \to \mathbb{R} $ 称为莫尔斯函数，如果对于任意 $ x \in \mathbb{R} $ 满足 $ f’(x) = 0 $，我们有 $ f’‘(x) \ne 0 $。

例 10。
- $ f(x) = x^2 $, $ f’(x) = 2x $, $ f’‘(x) = 2 $，则 $ f(x) $ 是一个莫尔斯函数。
- $ f(x) = x^3 $, $ f’(x) = 3x^2 $, $ f’‘(x) = 6x $，则 $ f(x) $ 不是莫尔斯函数。
- $ f(x) = x^3 - x $, $ f’(x) = 3x^2 - 1 $, $ f’‘(x) = 6x $，则 $ f(x) $ 是一个莫尔斯函数。

定理 11。 从上面的例可以看出，莫尔斯函数是丰富的。

为了更好地描述函数中的一些特殊点，我们引入了一个称为“临界点”的概念。

定义 12。 若 $ f’(x) = 0 $，则称点 $ x \in \mathbb{R} $ 为临界点。

对于莫尔斯函数，我们知道每个临界点都是局部极大点或局部极小点。

由于我们刚刚引入了纽结，因此很自然地要考虑莫尔斯函数与纽结之间的关系。

$$
h: \mathbb{R}^3 \to \mathbb{R}, \quad (x,y,z) \to z, \quad h \circ k: S^1 \to \mathbb{R}
$$

我们可以将纽结图与临界点联系起来。

定义 13。 莫尔斯 若 $ h \circ k $ 是莫尔斯函数，且若 $ x_0 \ne x_1 $ 是两个临界点，则 $ h \circ k(x_0) \ne h \circ k(x_1) $

定义 14. 对于一个莫尔斯纽结 $ k: S^1 \to \mathbb{R}^3 $，定义 $ b(k) $ 为 $ k $ 的局部极大点的个数。我们称 $ b(k) $ 为 $ k $ 的桥数。对于一个纽结类 $ K $，定义 $ K $ 的桥数 $ b(K) $ 为所有 $ b(k) $ 中的最小值。

例 15. $ b(\text{unknot}) = 1 $

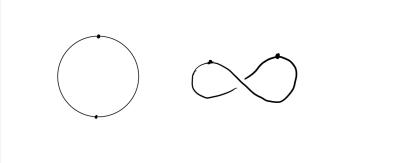
由于最小桥数为1，如上图所示，平凡结的桥数为1。

Therefore, If $ b(k)=1 $, then $ k=\text{unknot} $

因为我们已经证明了平凡结和三叶结不相同，所以三叶结的桥数必须大于1。

$$
b(\text{trefoil}) \ge 2
$$

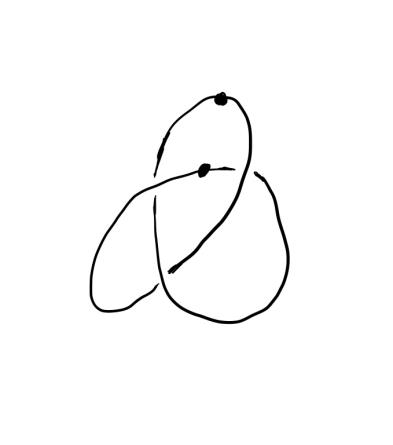
如上图所示，图中三叶结的桥数是2。因此，三叶结的桥数为2。

还有另一种方式来定义桥数：[4,5]

定义 16。 用 $ D $ 表示一个图，$ D= $ 中具有至少一个交叉点的弧称为桥。

例 17。 红色圆圈中的弧是桥。

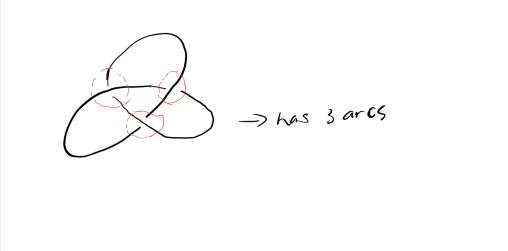
红色的弧不是桥

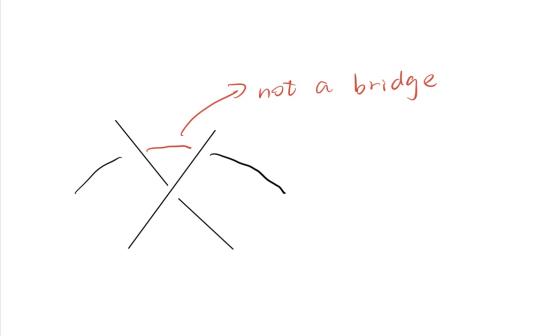
假设 $ K $ 是一个纽结。定义它的桥数 $ b_D(K) $ 为

$$
b(K) = \min_D b(D),
$$

其中 $ D $ 遍历 $ K $ 的所有图示。

定理 18. $ \min b(D) = \min b(k) = b(k) $

E. 亏格

本节中，我们将讨论纽结的亏格及其性质。

定义 19. 对于一个闭曲面 $ S $，我们将其亏格定义为 $ S $ 的“洞”的数量，并记作 $ g(S) $。

以下是不同亏格的例子。

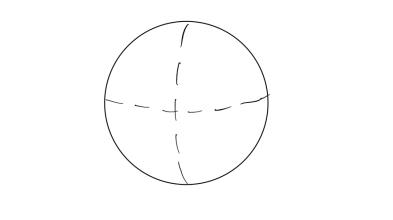
亏格: 0

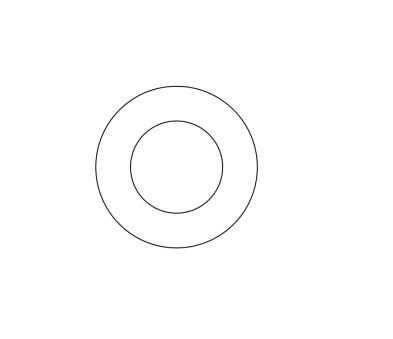
亏格: 1

F. 欧拉示性数

定义 20。 欧拉示性数 是纽结和拓扑不变量，是一个可用于描述拓扑空间形状或结构的数，无论其如何弯曲。通常记作 $ \chi $。

定理 23.
$$
\chi = V - E + F
$$
其中 $ V $ 表示顶点的数量，$ E $ 表示边的数量，$ F $ 表示面的数量。

根据公式，我们可以计算四面体的欧拉示性数。

例 21。 以四面体为例：

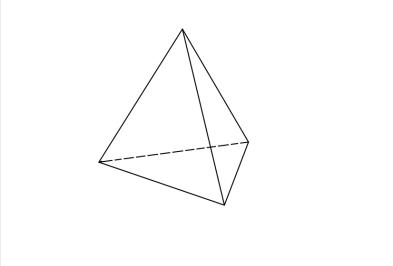
$ V = 4 $, $ E = 6 $, $ F = 4 $

$$
\text{Euler characteristic} = 4 - 6 + 4 = 2
$$

我们还可以计算环面的欧拉示性数。首先，需要沿图15中的红线切割环面。然后，再沿蓝线进一步将其切开。这样我们就得到了顶点 = 1、边 = 2 和面 = 1。

例 22。 对于一个环面

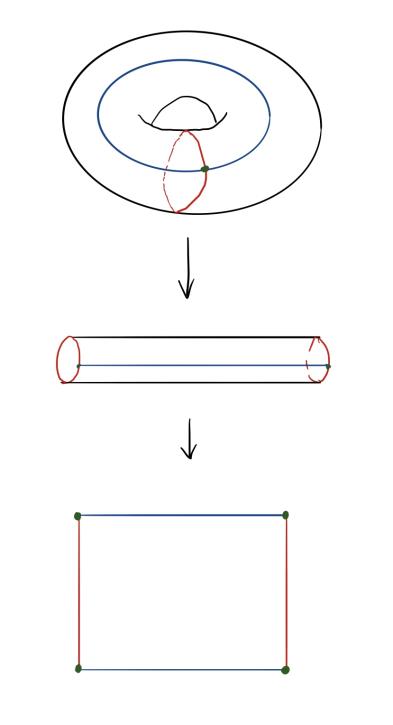
$ V = 1 $, $ E = 2 $, $ F = 1 $

因此，欧拉示性数等于：

$$
\text{Euler characteristic} = 1 - 2 + 1 = 0
$$

定理 24.
对于任意闭曲面 $ S $，有 $ \chi(S) = 2 - 2g(S) $。
对于带边曲面，有 $ \chi(S) = 2 - 2g(S) - b $，其中 $ b $ 是边界的数量。

对于有边界的曲面：

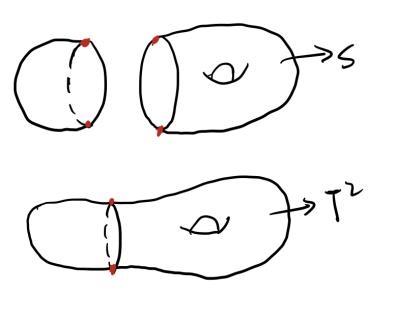
接下来，我们用 $ s $ 来计算环面 $ T^2 $ 的欧拉示性数：

$$
V(T^2) = V(s), \quad E(T^2) = E(s), \quad F(T^2) = F(s) + 1
$$

Therefore
$$
\chi(T^2) = \chi(s) + 1
$$

结论：
假设 $ S $ 有 $ b $ 个边界。$ T $ 是沿 $ S $ 的所有边界对 $ S $ 进行封顶后的结果。
则
$$
\chi(S) = 2 - 2g(S) - b
$$

定理. 两个闭定向曲面相同当且仅当它们具有相同的亏格。

证明。 对于任意闭曲面 $ S $, $ \chi(S) = 2 - 2g(S) $。对于带边曲面，$ \chi(S) = 2 - 2g(S) - b $。

假设 $ g = k $ 为真。
对于 $ g = k + 1 $

$$
\chi(S_{k+1}) = \chi(S_k) + \chi(T^2) - 2 = 2 - 2k + 0 - 2 = 2 - 2(k+1) = 2 - 2g(S_{k+1})
$$

G. 塞弗特曲面

本节主要讨论塞弗特曲面。以下是塞弗特曲面的定义。

定义 27。 如果曲面 $ S \subseteq \mathbb{R}^3 $ 满足以下条件，则称其为 $ K $ 的塞弗特曲面：
(1) $ S $ 的边界是 $ k $。
(2) $ S $ 是可定向的。

例 26。 一个纽结允许存在一个塞弗特曲面。

定义 29。 塞弗特算法：对于任意一个纽结的图示 $ k $，我们可以找到它的塞弗特曲面。

例 28。 给定纽结的一个任意方向。

$$
\chi(S) = 2 - 2g(s) - b = 2 - 2g(s) - 1 = 1 - 2g(s)
$$
又
$$
\chi(S) = 2 - 3 = -1 \quad \text{(添加一个半扭转会使欧拉数减少1。)}
$$
因此
$$
-1 = 1 - 2g(s) \Rightarrow g(s) = 1
$$

定义 30。 对于一个纽结 $ k $，定义 $ g(k) $ 为所有塞弗特曲面的最小亏格。
$$
g(k) = 0 \Leftrightarrow k \text{ 是一个平凡结}
$$

定义 31。 对于两个纽结 $ K_1 $ 和 $ K_2 $，定义它们的连通和满足：
$$
g(K_1 # K_2) = g(K_1) + g(K_2)
$$

推论：
如果 $ K_1 \ne \text{unknot} $, $ K_2 \ne \text{unknot} $，
则 $ K_1 # K_2 \ne K_1 $, $ K_1 # K_2 \ne K_2 $

定理 32.
$$
g(K_1 # K_2) = g(K_1) + g(K_2)
$$

证明。
步骤1: 证明 $ g(k_1 # k_2) \le g(k_1) + g(k_2) $。

为 $ K_1 $ 和 $ K_2 $ 选取最小亏格的塞弗特曲面，以构造 $ K_1 # K_2 $ 的塞弗特曲面。
$$
\chi(S) = \chi(S_1) + \chi(S_2) - 1
$$
$$
1 - 2g(S) = (1 - 2g(S_1)) + (1 - 2g(S_2)) - 1
$$
$$
g(S) = g(S_1) + g(S_2)
$$
因此
$$
g(k_1 # k_2) \le g(S) \le g(S_1) + g(S_2)
$$

步骤2: 证明 $ g(k_1 # k_2) \ge g(k_1) + g(k_2) $。

1. 选取一个最小亏格的塞弗特曲面 $ S $ 对应 $ K_1 # K_2 $。

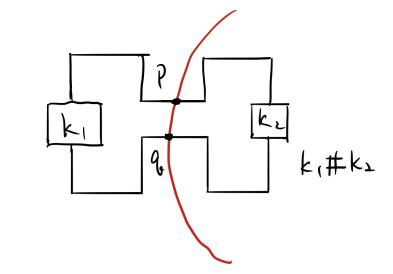
2. 找到一个二维球面 $ \Sigma $，使得 $ \Sigma \cap (K_1 # K_2) = p, q $。

一般来说，两个曲面沿曲线相交，且这些曲线可以有边界。根据定义，$ S $ 的塞弗特曲面是一个可定向曲面，且 $ S $ 的边界是 $ K_1 # K_2 $。因此，
$$
\partial(S \cap \Sigma) = \partial((K_1 # K_2) \cap \Sigma) = p, q
$$
令
$$
S \cap \Sigma = \alpha \cup \beta_1 \cup \cdots \cup \beta_n
$$
因为 $ \beta_1, \beta_2, \ldots, \beta_n $ 是闭曲线，没有边界，所以 $ S \cap \Sigma $ 的边界仅为 $ p, q $。

3. 如果 $ n = 0 $，
   那么 $ S \cap \Sigma = \alpha $, $ \partial\alpha = p, q $。
   我们可以沿 $ \alpha $ 切割 $ S $，然后得到 $ S_1 $ 和 $ S_2 $，其中 $ \partial S_1 = K_1 $, $ \partial S_2 = K_2 $。
   因为 $ g(S) = g(S_1) + g(S_2) $，所以
   $$
   g(K_1 # K_2) = g(S) = g(S_1) + g(S_2) \ge g(K_1) + g(K_2)
   $$

4. 如果 $ n = 1 $，
   $ S \cap \Sigma = \alpha \cup \beta_1 $, $ \partial\alpha = p, q $。

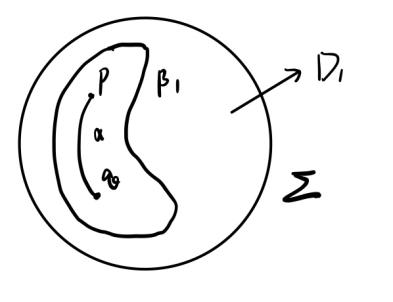
如上图所示，$ \beta_1 $ 边界一个圆盘 $ D_1 \subseteq \Sigma $。考虑 $ \beta_1 $ 在 $ S $ 上的情况，有三种可能。

情况1

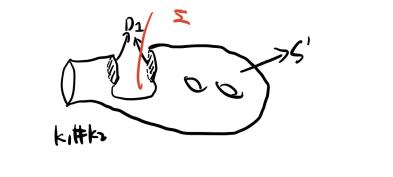
我们沿 $ \beta_1 $ 切割 $ S $，然后将 $ D_1 $ 粘贴到 $ S $，于是得到 $ S’ $。如图所示，$ g(S’) = g(S) - 1 $。
这是不可能的，因为我们已经选取 $ S $ 作为具有最小亏格的塞弗特曲面。

情况2:

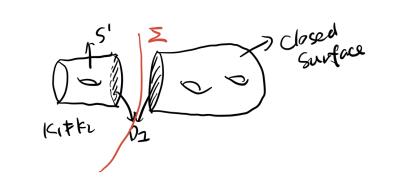
由于右部分是闭曲面，我们忽略该部分，将左部分视为 $ S’ $。原因同上，$ g(S’) < g(S) $ 不可能。

情况3：

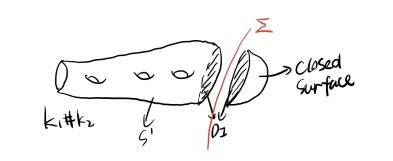
在这种情况下，$ g(S’) = g(S) $。切割后，$ \beta_1 $ 不存在。因此 $ S’ \cap \Sigma = \alpha $。

5. 对于一般的 $ n $：
   我们可以使用归纳法。由于 $ n = 0 $ 成立，并且通过将 $ n = 1 $ 变为 $ n = 0 $ 来证明 $ n = 1 $。因此我们归纳假设 $ n - 1 $ 成立时，可以证明 $ n $ 也成立。
   对于 $ n $:
   $$
   S \cap \Sigma = \alpha \cup \beta_1 \cup \cdots \cup \beta_n
   $$
   存在某个 $ \beta_i $ 边界一个圆盘 $ D_i $ 使得 $ D_i \cap S = \beta_i $。
   我们可以通过在步骤4中使用相同的方法将 $ n $ 减少到 $ n - 1 $。
   因此，我们可以应用归纳假设。

三、结论

本文讨论了不同的纽结不变量。文章从纽结的基本定义开始——knot是嵌入在 $ \mathbb{R}^3 $ 中的一个嵌入圆 $ S^1 $。然后我们使用纽结图来对纽结有一个大致的认识。由于纽结的形态变化多样，我们将纽结划分为若干类型，这有助于进一步讨论。但划分纽结的标准是什么？很自然地，我们需要寻找一些纽结的不变量，以帮助我们识别不同类型的纽结。因此，本文其余部分讨论了纽结不变量。第一个是三色性，其基本含义是：一个纽结的三色性是指该纽结能够按照特定规则用三种颜色进行着色的能力。第二个是莫尔斯函数，它与三色性略有不同，因为莫尔斯函数将纽结图转化为数值和函数。第三个是欧拉示性数，这部分内容结合塞弗特曲面进行了讨论。本文所提到的纽结不变量从不同角度探索了纽结，为我们提供了更广阔的视角。