题目
开始有nnn个物品按从左到右的顺序排成一行,第iii个物品有一个代价aia_iai和一个价值bib_ibi。每次操作,你可以选择两个相邻的,并且代价之和不超过KKK的物品,将它们从序列中删去,并获得两个物品价值之和的收益。每次删去这两个物品后,就认为这两个物品的左边和右边的就变成相邻的了。求最大化价值。
n≤800n\le 800n≤800
比赛没打,赛后看了看题,十分一眼,看正解好像也是这样搞的
早上状态就是香,一眼区间dp,fl,rf_{l,r}fl,r表示消除 lll 到 rrr 的最大价值,按照以往的思路,显然 fl,r=maxl≤k<r(fl,k+fk+1,r)f_{l,r}=max_{l\le k<r}(f_{l,k}+f_{k+1,r})fl,r=maxl≤k<r(fl,k+fk+1,r)。
但是这种情况是不包括中间全消去,两边变成相邻消去的情况的。那我就把这种情况的最简状态考虑一下,也就是当中间消去,lll 和 rrr 成为相邻且消去时
fl+1,r−1=suml+1,r−1al+ar≤Kf_{l+1,r-1}=sum_{l+1,r-1}\\a_l+a_r\le Kfl+1,r−1=suml+1,r−1al+ar≤K
对于这种情况而言,fl+1,r−1=suml,rf_{l+1,r-1}=sum_{l,r}fl+1,r−1=suml,r 一定最优
综上所述,
fl,r={suml,rfl+1,r−1=suml+1,r−1且al+ar≤Kmaxl≤k<r(fl,k+fk+1,r)else f_{l,r}=\left\{
\begin{array}{rcl}
sum_{l,r} && {f_{l+1,r-1}=sum_{l+1,r-1}且a_l+a_r\le K}\\
max_{l\le k<r}(f_{l,k}+f_{k+1,r}) && {else}\\
\end{array} \right. fl,r={suml,rmaxl≤k<r(fl,k+fk+1,r)fl+1,r−1=suml+1,r−1且al+ar≤Kelse
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=810;
int n,K,a[maxn],b[maxn],f[maxn][maxn],s[maxn];
signed main()
{
cin>>n>>K;
for(int i=1;i<=n;i++)
{
cin>>a[i]>>b[i];
if(i>1&&a[i]+a[i-1]<=K) f[i-1][i]=b[i-1]+b[i];
s[i]=s[i-1]+b[i];
}
for(int len=3;len<=n;len++)
for(int l=1;l+len-1<=n;l++)
{
int r=l+len-1;
if(f[l+1][r-1]==s[r-1]-s[l]&&a[l]+a[r]<=K) f[l][r]=s[r]-s[l-1];
else for(int k=l;k<r;k++)
f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]);
}
cout<<f[1][n]<<endl;
return 0;
}
一点小收获
-
对于区间dp而言,要对于某种情况的最简状态抽象出来,而不要去想复杂的包含很多特定情况下的复杂状态。
-
考虑合并正确性的时候,不要孤立地去仅限于特定的两个子区间去想
比如这道题,刚思考合并的时候,会陷入一个误区,也就是当两个子区间均有剩余时,剩余还能合并,抽象成最简状态就是
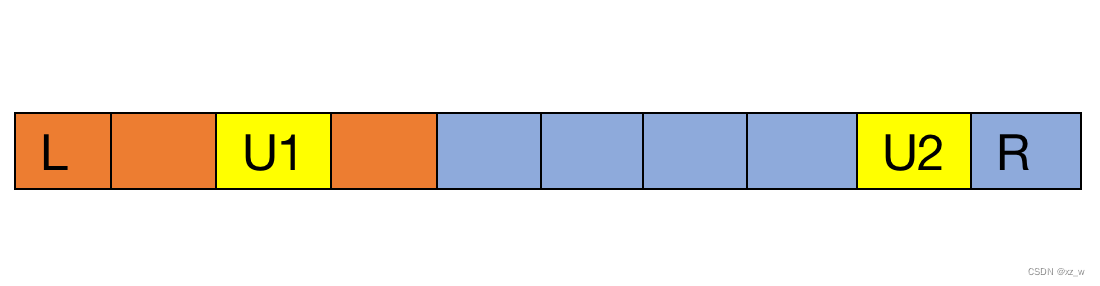 (U1与U2能合并,但是其均不能与其所在区间合并)
(U1与U2能合并,但是其均不能与其所在区间合并)然后竟然想对每个状态开个vector,但好在马上我就否定了这种情况
因为事实上会取到另两个子区间
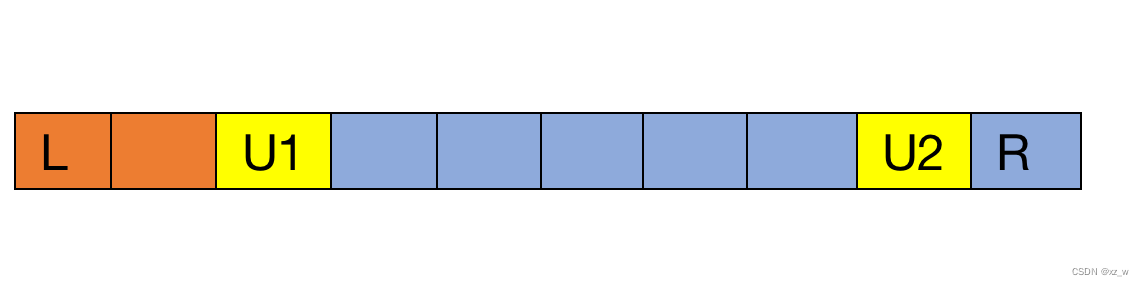
然后对于子区间,直接最优的合并。





 本文介绍了一种区间动态规划问题的解决方法,通过合理抽象最简状态来优化算法。具体讨论了如何在删除代价不超过K的相邻元素以最大化价值的问题中应用这一技巧。
本文介绍了一种区间动态规划问题的解决方法,通过合理抽象最简状态来优化算法。具体讨论了如何在删除代价不超过K的相邻元素以最大化价值的问题中应用这一技巧。

















 225
225

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








