去中心化控制优化通信

去中心化控制用于优化与不可行区域的通信

斯蒂芬妮·吉尔、塞缪尔·普伦蒂斯、尼古拉斯·罗伊和达尼埃拉·鲁斯

摘要

本文提出了一种去中心化梯度控制器，用于优化移动空中飞行器与静止地面传感器车辆在存在不可行区域的环境中的通信。我们将问题建模为混合整数二次规划，该优化公式易于实现，并且我们证明了通过引入缩放矩阵可以影响智能体轨迹绕行不可行区域，从而扩大可达到的收敛解的范围。我们在三维仿真中验证了该控制器在智能体故障情况下的鲁棒性，并在室内环境中进行了10次包含四旋翼飞行器和地面传感器的多智能体硬件实验。最后，我们提供了理论保证，证明该控制器能够严格地在智能体轨迹上最小化非凸代价，这一特性对于一般的多智能体协调任务而言是理想的。

1 引言

去中心化控制使得机器人系统能够实现复杂的群体行为，例如会合、编队保持和覆盖，并将其应用于广泛的工程问题中；然而，由于缺乏集中式计算，对通信质量的要求也随之提高[1–4]。本文聚焦于移动机器人多智能体网络与平稳传感器之间优化通信质量的问题。在先前的研究[5]中，我们开发了一种可证明优化通信质量的去中心化梯度控制器

网络，但这种方法仅限于整个空间均可行的环境。在实际场景中，例如图1所示的室内环境，通常存在危险或不可通行的空间区域。这些障碍物使得控制器的设计变得困难，主要原因有两个：（1）目标状态或最优通信配置先验未知；（2）不可行区域的存在引入了许多受约束的局部极小值，可能导致较差的解。本研究采用非线性优化技术，设计一种易于实现的去中心化控制器，以解决在存在不可行区域的情况下进行通信优化的问题。

引入不可行区域带来了许多挑战。通信优化问题的代价是非凸的，这是许多有趣的分布式任务所必需的性质[6]。因此，我们旨在设计易于实现的控制器，这些控制器具有可扩展性、仅依赖局部信息以及能够沿着每个智能体的轨迹降低代价的理想特性。基于梯度的控制器因此非常合适。然而，不可行区域的存在将自由空间分割为多个需要进行优化的子集，这给收敛性以及收敛解的质量带来了挑战。例如，空中飞行器可能会在代价的最速下降方向恰好垂直于障碍物边缘时（如图2b所示），被“困”在一面墙后方，而实际上它本可以轻松绕过该墙，所以我们需要考虑更广泛的下降方向以避免此类情况。由于在非凸环境中进行基于梯度的优化，所能实现的收敛结果要么是代价的临界点（在最佳情况下），要么是在不可行区域边界上代价有所改善的点。我们的目标是推导出一种控制器，使得智能体在其生成的轨迹上能够降低代价，并且这些

轨迹偏向于避开不可行区域的方向，从而具有更广的可实现改进代价解的范围。

利用非线性优化中的梯度投影法[7]使我们能够将非凸问题表述为一个简单的二次规划问题，其中约束集是环境中自由空间的一个凸子集。我们使用混合整数规划的解来有效选择进行代价优化的凸可行域，从而得到一个混合整数二次规划（MIQP），该规划可针对每个智能体高效求解。我们表明，引入一个缩放矩阵——该矩阵保持了问题的二次性和可高效求解的特性——允许设计者影响车辆轨迹绕行不可行区域，并改善可达到的收敛解的范围。

特别地，在第3.2.1节中，我们推导出航向角与选定缩放矩阵下的最速下降方向之间的分析结果，并证明了代价下降性质得以保留。定理3表明，存在一个缩放矩阵序列，使得我们的算法能够生成到达通信代价无约束局部极小值的轨迹，前提是对于给定的初始位置和环境存在这样的轨迹。尽管目前仍是一个开放问题，即如何推导出能保证收敛到代价无约束局部极小值的缩放矩阵序列，但在结果部分，我们提供了一种启发式选择缩放矩阵的方法，在仿真和硬件实验中表现出良好的性能。

第4.1节介绍了我们的通信优化算法，并展示了控制器的性能及其在智能体故障情况下的鲁棒性。最后，在第4.2节中，我们在真实飞行器上验证了我们的控制方法，这些飞行器必须在室内环境中导航（图1），以优化三个平稳的地面车辆组成的网络之间的通信。

1.1 相关工作

用于避障的人工势场，如[8–10],中通过不同图概念对环境进行分解以搜索空间[11, 12],，以及如[13],中的最短路径方法，代表了有障碍物环境中车辆协同问题的活跃研究方向。在当前工作中，智能体的最终位置是通信代价的局部极小值，由于该代价需迭代优化，这些局部极小值先验未知。因此，我们无法假设已知可导航的最终目标状态，也无法禁止极小值位于不可行区域内。

优化问题本身定义智能体轨迹这一特性使得该问题尤为具有挑战性。文献[14]也研究了一个多智能体优化问题，但针对的是二维环境的覆盖，并采用了巧妙的映射反演方法。在思想上与我们的工作类似的方法包括混合整数方法[15, 16], ，尽管这些方法的不同之处在于它们还考虑了向已知目标状态的导航。在我们的研究中，必须沿智能体轨迹降低代价，因为代价收敛到局部极小值以及网络的连通性保持都依赖于这一要求。因此，本研究的一个强烈动机是确保在每次迭代中都能实现代价的下降。在车辆轨迹上可证明地降低代价这一要求在许多协同任务中都很常见，从而说明了通信优化问题对其他多智能体任务的通用性[2–4]。

2 问题描述

在之前的工作[5],中，我们推导出了一种代价函数，用于优化空中飞行器与地面传感器之间的通信质量。该代价函数使用信干比（SIR）来衡量一对飞行器之间的通信强度，并考虑来自邻近飞行器的干扰，其形式为两项的加权和：第一项最大化每条链路的信干比，第二项均衡所有链路的信干比。控制器的最终行为通过增加或减少标量q进行设计，q用于为代价函数中的第二项分配更高或更低的权重。

代价H : R^(p×N) → R 在第 k 次迭代时针对 N 个飞行器的所有车辆位置 x_k^i ∈ R^p 定义为：

$$
H(x_k^1,…, x_k^N) = \sum_i \sum_{j≠i} \left( -SIR_{ij} + q \frac{SIR_{ij}}{SIR_{ij} + d} \right)
$$

其中，i 和 j 分别是位置为 xi 和 xj 的飞行器的简写，d 是一个任意小的正数，用于允许 SIR_ij = 0。信干比 (SIR): R^p → R 由公式 $SIR_{ij} = \frac{f_{ij}}{N_i + \sum_{k∈N_{i\setminus j}} f_{ik}}$ 给出，两个通信智能体 i 和 j 之间的信号强度由 f_ij: R^p → R 给出。信号强度由 $f_{ij} = P_0 β^{-d_{ij}}$ 给出。i 邻域中除 j 外的所有飞行器记为 N_{i\setminus j}；P_0 ∈ R 为给定的最大信号强度，β 为给定的衰减参数，通常 β = 2，且 d_ij = ‖x_i − x_j‖。

2.1 将通信优化作为混合整数二次规划

我们希望沿着降低代价H(x_k)的轨迹移动N个智能体，其中x_k ∈ R^(p×N)是时间k时所有车辆位置的向量，同时约束该轨迹在所有时间内保持在不可行区域之外。对于在迭代k时位置为x_k^i ∈ R^p的每个车辆i，我们希望沿最速下降方向 −∇H(x_k) 移动一个量s_k > 0，但必须施加约束以保持在自由空间内。值 ∇_i H(x_k) ∈ R^p 是代价H关于时间k时车辆xi位置的梯度。我们注意到，尽管代价是全局的，但导数∇_i H(x_k)仅依赖于局部信息，在这个意义上是分布式的。

随后，为了简化符号表示，我们省略下标i，使得x_k表示车辆i的位置，∇H(x_k)表示代价H关于代理i位置的梯度。

非线性优化中的梯度投影方法使我们能够在保持凸集约束的同时，对非凸代价函数进行下降优化。由于环境的自由空间几乎从不是凸的，我们必须将自由空间集合划分为多个凸集的交集，而对于具有凸多边形不可行区域的环境（这正是我们所考虑的情况），这种划分是可行的。我们利用每个智能体仅需在其局部环境中对H进行优化这一特点，采用混合整数规划来激活自由空间的一个局部凸子集，从而在该子集上执行梯度投影。最终得到的是一个混合整数二次规划（MIQP）：

$$
\begin{aligned}
& \min_{x,t} |x - (x_k^i - s_k ∇ i H(x_k))|^2 \
& \text{s.t.} \quad A_l x ≤ b_l + t_l M, \quad ∀l ∈ {1,…, L} \
& \quad \sum {j=1}^{E_l} t_l^j ≤ E_l - 1, \quad ∀l ∈ {1,…, L} \
& \quad t_l^j ∈ {0, 1}, \quad ∀j, l
\end{aligned}
$$

其中，s_k是一个标量>0，L 是环境中多边形不可行区域的数量，E_l是不可行区域 l 的边数，M 是一个足够大的标量，t_l ∈ R^{E_l}是由 MIQP 为每个不可行区域返回的二进制列向量，A_l ∈ R^{(E_l × p)}; b_l ∈ R^{E_l}用于描述如下定义的凸多边形不可行区域。接下来，我们给出由 MIQP 返回的不可行区域与自由空间集合的数学描述：

定义 1（不可行区域与自由空间集合） 不可行区域是凸的多边形集合，为 E_l 个半空间 $\bigcap_{i=1}^{E_l} (A_i x ≤ b_i)$ 的交集。车辆不能穿过不可行区域，但我们假设通信强度不受影响。来自（2）的二进制列向量编码了可行区域的约束条件，因此二进制变量的一个特定解 t* ∈ R^{L E_l} 实际上会“激活”每个不可行区域的一条或多条边界，使得这些被选中的边界在求解混合整数二次规划时作为有效的约束条件。被激活的障碍物边界所对应的半空间的交集始终是一个闭合且凸的集合，记为

$$
X_{F(t )} = X_F(t ) = {x | A_l x ≤ b_l + t*_l M}
$$

其中 X_F(t ) 是对应于二进制变量解 t 的闭合凸自由空间子集，如式（2）所示。

式（2）中优化公式的直观含义是：每个车辆在保持处于可行空间内的前提下，尽可能沿代价函数 H 的最速下降方向移动。然而，该优化公式的问题在于，如果最速下降方向垂直于某个不可行区域的边界，则有可能被困在该边界后方，即使实际上车辆可以通过沿一个非最速下降的下降方向轻松绕过该障碍物，参见图 2b。我们将在下一节的优化公式中解决此问题。

2.2 使用缩放以避免不可行区域

上一节中的混合整数二次规划公式可以使用现成优化器高效求解，并得到形式非常简单的控制器，但其局限性在于始终沿最速下降方向行进，即使该方向被不可行区域所阻碍。因此，我们希望在保持上一节混合整数二次规划简单性的同时，提高可实现解的范围。为此，我们提出采用缩放梯度投影法。

在非线性优化理论中，缩放梯度投影法常用于提高收敛速度[7]。然而，我们的目标是影响车辆轨迹向不垂直于活跃约束的方向移动

边。此外，缩放梯度投影法相当于在优化变量x中增加了一个二次项，因此同样是一个二次规划问题，与之前的情况相同，可以轻松求解。我们定义一个新的问题，其优化结果为代理i（其中下标i被省略）生成一个可行的航路点 x̄_k^S。

$$
\bar{x} k^S = \arg\min_x |x - z_k| {S_k}
$$

s.t. A_l x ≤ b_l + t_l M ∀l
∑_{j=1}^{E_l} t_l^j ≤ E_l - 1 ∀l ∈ {1,…, L}
t_l^j ∈ {0, 1} ∀j, l

其中矩阵 S_k ∈ R^{p×p} 是一个正定矩阵，我们使用符号 ‖q‖_{S_k} = √(q^T S_k q)；∀q ∈ R^p 表示缩放范数。对于这种缩放后的优化公式，期望的航路点是

$$
z_k = x_k - s_k (S_k)^{-1} ∇H(x_k)
$$

一种更紧凑的定义（4）可以利用来自（3）的自由空间集合表示，针对每个求解（4）的二进制变量t*向量来书写：

$$
\bar{x} k^S = \arg \min {x ∈ X_F(t*)} |z_k - x|_{s_k}
$$

x_{k+1}的位置更新规则由以下公式给出：

$$
x_{k+1} = x_k + α_k (\bar{x}_k^S - x_k) = x_k + α_k d_k
$$

其中步长 α_k 和 s_k 满足假设 1：

假设1 存在足够小的步长α_k > 0和s_k > 0，使得给定一个下降方向d_k后，沿此方向的一步不会与障碍物相交，并且在Armijo意义下或非线性规划[7]中的标准有限最小化准则意义下，能够使代价充分减小。我们假设在整个论文中α_k和s_k均满足这些条件。

在当前点 x_k 处对代价进行一阶泰勒展开表明，沿有效的下降方向 d_k，只要步长足够小，便可实现代价下降。当当前迭代点位于障碍物边缘时，为了避免与障碍物相交，步长必须为零，此时方法将停止。要求 S_k 是正定的，以确保代价的下降性 H(x_{k+1}) < H(x_k)。实际上，我们的下一个航路点 x_{k+1}将在缩放范数的意义下最小化到目标航路点 z_k [7]的距离。参见图2。

我们定义下降方向 d_k = x̄_k^S - x_k。其优点在于，现在我们可以将轨迹引导至相对于最速下降方向 −∇H(x_k) 的任意航向，只要该方向满足 d_k = x̄_k^S - x_k 且 (−∇H(x_k))^T d_k < 0，其中 x′y 是向量 x 与向量 y 的点积，图2中所示的相对航向角 h 定义为：

$$
h = \arccos \left( \frac{(−∇H(x_k))^T d_k}{|∇H(x_k)| |d_k|} \right)
$$

我们利用这种灵活性来优先选择完全避开沿负梯度方向的不可行区域的路径。在第 3节中，我们推导出 S_k 与 h 之间的解析关系。

3 分析

3.1 未缩放控制器的分析

我们证明，由MIQP结合公式(7)中的更新规则所产生的车辆位置序列会产生严格的下降方向，使得H(x_{k+1}) < H(x_k)对所有满足假设k的步长均成立1。由于二进制变量t在方程(2)中的解通常不唯一，这导致我们难以证明代价的下降性，即H(x_{k+1}) − H(x_k) < 0。这种非唯一性进一步意味着，我们进行优化的凸子集可能不是唯一的，且可能不包含当前迭代点x_k，从而使经典的梯度投影法的下降性证明不再适用。

根据结果可知，代价在每次迭代中都会减小，并且根据先前的研究表明，H的局部极小值是有限的，[5],我们预期会收敛到一个稳定点。该定点可能位于不可行区域的边界上，此时投影 x̄_k = x_k（平稳）如引理1.4中所定义，也可能是一个代价函数H的临界点。在下一节中，我们将展示如何利用缩放来降低停留在不可行区域边界而“陷入”的可能性。

我们使用向量d具有梯度相关性的概念。

定义2 （梯度相关） 对于任何收敛到非平稳点的子序列 {x_k} {k∈K}，若一个有界方向序列 {d_k} {k∈K} 满足以下条件，则称其为梯度相关的：

$$
\limsup_{k→∞, k∈K} ∇H(x_k)^T d(x_k) < 0, \quad ∀k ∈ K
$$

我们使用来自[7]的投影的以下性质：

引理 1（凸集 X 上投影的性质） 设 X 是非空、闭集且凸的，令 [z]+ 表示将 z ∈ R^p 投影到 X 上的结果：
1. z ∈ R^p 的投影存在，唯一，并且在x ∈ X上最小化‖z − x‖。
2. 必须满足 (z − [z]+)^T (x − [z]+) ≤ 0，对所有x ∈ X成立。
3. 投影函数是连续的。
4. 对所有s > 0，我们有~x = [~x − s∇H(~x)]+ 当且仅当~x是平稳的。

我们现在希望证明，由d_k求解(2)所得的结果对于所有k均是梯度相关的，因此对于满足假设1的步长，我们有H(x_{k+1}) < H(x_k)。

定理 1 对于处处可微的代价H，通过求解混合整数二次规划公式并使用来自 {d_k}的更新规则所生成的方向序列是代价的下降方向，且这些方向满足对于非代价平稳点的点x_k的梯度相关性质。

证明 该证明与定理 2的证明相同，只需将缩放矩阵设为单位矩阵S_k = I。 □

3.2 避免不可行区域的缩放梯度投影法分析

我们为与MIQP（4）的缩放版本相关的三个主要问题提供了分析结果。首先，我们将缩放矩阵 S_k 与相对航向角 h 关联起来，其中该方向是相对于最速下降方向而言的。其次，我们证明了使用缩放矩阵可为每个智能体生成在每次迭代中代价均下降的轨迹。最后，我们证明存在一个缩放矩阵序列{S_k}，使得由（4）中的优化公式生成的轨迹收敛到更理想的 无约束 局部极小值 H，前提是该环境存在这样的轨迹。尽管推导此类缩放矩阵序列的问题仍未解决，但在结果部分，我们提供了一种生成缩放矩阵的启发式方法，该方法可以绕过不可行区域，但不能保证收敛到H的无约束局部极小值。

3.2.1 控制相对航向角以避免不可行区域

在本节中，我们将深入了解如何设计缩放矩阵以实现期望的相对航向角h。根据第2.2节的讨论，我们要求缩放矩阵S_k必须是一个正定矩阵，并且具有正交

选择特征向量 v_i ∈ R^p，我们可以将 S_k 写成分解形式 S_k = V K V^T，V = [v_1,…, v_p] 是 S_k 的特征向量矩阵，K ∈ R^{p×p} 是 S_k 的特征值 [k_1,…, k_p] 构成的对角矩阵。此外，我们知道所有 k_i > 0 均为正数，因为 S_k 是正定的。因此，我们可以将 R^p 中的任意向量，特别是负梯度向量 −∇H(x_k)，表示为 v_i 的线性组合。具体而言，我们可以写出 −∇H(x_k) = Σ_{i=1}^p f_i v_i，其中 f_i 是标量，表示 −∇H(x_k) 在 v_i 方向上的分量，我们考虑归一化特征向量，使得 ‖v_i‖ = 1。根据勾股定理以及 v_i 相互正交的事实，我们有

$$
|∇H(x_k)|^2 = \sum_{i=1}^p (f_i v_i)^T (f_i v_i) = \sum_{i=1}^p (f_i)^2
$$

我们表示未投影的航向方向 d̃_k，并注意到这对于缩放梯度投影是 d̃_k = z_k − x_k。由(5)可知，这仅仅是 s_k (S_k)^{-1} ∇H(x_k)。如果我们再次使用勾股定理来写出 ‖d̃_k‖, 以及点积 ∇H(x_k)^T d̃_k 的表达式，可得：

$$
|d̃ k|^2 = s_k^2 \sum {i=1}^p \left(\frac{1}{k_i}\right)^2 f_i^2
$$

$$
∇H(x_k)^T d̃ k = s_k \sum {i=1}^p \frac{1}{k_i} f_i^2
$$

使用点积的定义以及定义(10)、(11)和(9)，我们得到一个通过其特征向量和特征值将相对航向角h与缩放矩阵S_k关联起来的表达式：

$$
\cos(h) = \frac{(−∇H(x_k))^T d̃ k}{|∇H(x_k)| |d̃_k|} = \frac{\sum {i=1}^p \frac{1}{k_i} f_i^2}{\sqrt{\sum_{i=1}^p \left(\frac{1}{k_i}\right)^2 f_i^2} \cdot \sqrt{\sum_{i=1}^p (f_i)^2}}
$$

该表达式表明，通过精心选择缩放矩阵的特征向量和特征值，可以设计其以实现特定的相对航向角。特别地，我们注意到，如果S_k = I，其中I是单位矩阵，且k_i = 1 ∀i，则cos(h) = 1，航向角为零，此时我们沿最速下降方向移动，符合预期。相反，若对S_k的特征值k_i赋予更大权重，使得k_j ≫ k_i，∀j ≠ i，则会使航向方向 d̃_k 与 −∇H(x_k) 在v_i方向上的分量尽可能对齐。图 2给出了二维情况的示意图。然而，当k_i的比值变得更大时，速率的

收敛变得较慢，因此通常航向角h不应比必要值更大。

最后，(12)的一个结果是，对于正定缩放矩阵 d̃_k 的方向永远不可能与负梯度在垂直方向上一致。当特征向量 S_k v_i 趋近于与 −∇H(x_k) 垂直的方向时，负梯度向量沿该方向的分量 f_i → 0 随之趋近于零，因此，从公式(10)可以看出， d̃_k 不可能被调整为沿与 −∇H(x_k) 垂直的方向移动。

去中心化控制用于优化与不可行区域的通信

3.2.2 缩放梯度投影法的分析

在上一节中，我们展示了添加缩放矩阵 S_k 使我们能够灵活设计相对航向角，以避免环境中出现不可行区域。现在我们证明由此产生的方向 d_k = x̄ k^S − x_k （其中 x̄_k^S 由公式(4)求解得到）是下降方向，从而确保代价在智能体轨迹上减小。与未缩放情况类似，由于(4)中的二进制t变量通常不唯一，寻找适用于我们问题的下降方向 d_k 具有挑战性。根据梯度相关性的定义，我们希望证明的性质是：对所有 k 和迭代 k 上的所有解 d_k < 0，均有 ∇H(x_k)^T d_k < 0。我们证明方法的直观思路是：利用在包含当前迭代点的凸子集上定义的解 d_k^1（可证明该解始终具有梯度相关性），来约束因二进制变量不同取值而产生的所有其他解 d_k^t。由此我们可以证明，对所有 d_k^t 和 k，均有 ∇H(x_k)^T d_k < 0。利用 d_k 在所有迭代 k 上均满足梯度相关性的结论，并结合假设1，我们可得出每次迭代均实现代价下降，即 H(x {k+1}) < H(x_k)。

为避免繁琐的符号，我们随后将从 x̄_k^S 中省略S下标，并且读者应假设本节中的所有投影 x̄_k 均为缩放投影。如果一个点x_k 不等于它的投影，即 x̄_k ≠ x_k，则称该点为非平稳的。

定理2 对于处处可微的代价H : R^(p×N) → R，记通过求解(4)中的缩放的混合整数二次规划形式并使用(7)中提供的更新规则所产生的车辆位置序列{x_k}，我们有所有方向d_k 都是代价的下降方向，且它们满足对于所有非平稳的x_k 的梯度相关性质。

证明 ：我们将包含当前迭代点 x_k 的集合记为 X_F^1，将 z_k 在 X_F^1 上的投影记为 x̄_k^1，并注意到这是在该集合上求解缩放后的混合整数二次规划（MIQP）(6) 的一个解。

根据引理1.2 推广到缩放投影的情形，对于 x_k ∈ X_F^1 且 x̄_k^1 ∈ X_F^1，有 (z_k − x̄_k^1)^T (x − x̄_k^1) ≤ 0 成立。展开此性质，并利用 z_k 的定义、投影的连续性，以及我们考虑的是在包含当前迭代点 x_k 的单个集合 X_F 上进行投影的事实，可得对所有 k（见 [7]）：

$$
s_k ∇H(x_k)^T (x̄ k^1 − x_k) + |x̄_k^1 − x_k| {S_k}^2 ≤ 0, \quad ∀k
$$

□

术语 |x_k − x̄ k^1| {S_k}^2 ≥ 0 对于所有 S_k 正定且 x_k 非平稳的，使得 x_k ≠ x̄_k^1。因此由(13)式及引理 1.4 可得：

$$
|x_k − x̄ k^1| {S_k}^2 > 0 \Rightarrow s_k ∇H(x_k)^T (x̄_k^1 − x_k) < 0
$$

使得方向 d_k^t 对于属于同一凸子集的 x_k 和 x̄_k^1 始终是梯度相关的，其中 x_k 是非平稳的。我们稍后将再次使用该不等式。我们的目标是证明由方程（4）的解产生的所有方向 d_k^t = x̄_k^t − x_k 满足：

$$
−∇H(x_k)^T (x̄_k^t − x_k) < 0, \quad ∀k
$$

因为 x̄_k^1 是 z_k 到 X_F^1 上的投影的一个有效解，我们知道，缩放后的混合整数二次规划（4）的任意解 x̄_k^t 必须位于由下式定义的椭圆集合内：

$$
E_1 = \left{ c \mid (c − z_k)^T S_k (c − z_k) ≤ r_S^2 \right}, \quad r_S := (x̄_k^1 − z_k)^T S_k (x̄_k^1 − z_k)
$$

现在我们可以写出希望证明的梯度相关条件为：

$$
−f^* = \min_{x̄_t} \left[ −∇H(x_k)^T (x̄_t − x_k) \right]
$$

s.t. x̄_t ∈ E_1

其中我们期望的条件是 −f^* > 0，这确保了方向 (x̄_t − x_k) 是梯度相关的。

上述写出的最小化问题是适定的，因为f是在紧集E_1上被最小化的连续函数，因此存在最小值。此外，该问题可以使用拉格朗日乘子通过闭式求解，从而得到如下条件：

$$
−f^* = −r_S + s_k |∇H(x_k)|_{S_k}^2 − 1 > 0
$$

如果我们进一步将（定义代入 r_S ，从（16）中得到，并两边同时乘以（−1），展开并化简，便可得到我们希望证明的不等式条件的新形式：

$$
2 s_k ∇H(x_k)^T (x̄_k^1 − x_k) + (x̄_k^1 − x_k)^T S_k (x̄_k^1 − x_k) < 0, \quad ∀k
$$

我们将条件与（14）进行比较。根据（14）中所示的推理，我们知道 2 s_k ∇H(x_k)^T (x̄_k^1 − x_k) < 0 对于 x̄_k^1 ≠ x_k 成立，这是由非平稳性假设所保证的。因此，我们得出该期望不等式始终成立，所有生成的 d_k 都是期望的下降方向，这完成了证明。

为了获得更直观的理解，请注意公式(19)中的条件等价于要求 r_S = (x̄ k^1 − z_k)^T S_k (x̄_k^1 − z_k) < r {Sc} = s_k |∇H(x_k)| {S_k}^2 − 1。直观上，这意味着 x̄_k^1 是期望航路点 z_k 的一个有效投影，且在缩放范数意义下，从 x̄_k^1 到 z_k 的距离比从 x_k 到 z_k 的距离更小，即满足 |x̄_k^1 − z_k| {S_k} < |x_k − z_k|_{S_k}。

由于我们在每次迭代中都实现了代价下降，并且是在紧集上优化一个连续函数，因此极小值是明确定义的，如[5]所示，所以我们预期会收敛到一个固定点。该点可能位于不可行区域的边界，或位于代价的临界点，尽管使用缩放的目的是避开那些内部不包含局部极小值的不可行区域。

3.3 最优缩放矩阵序列的存在性

由于我们优化的是非凸代价，因此目标是收敛到局部极小值。对于这些局部极小值在可行空间内可达的情况，我们认为缩放矩阵序列 {S_k} 是“最优”的，如果使用算法1得到的控制器能为所有飞行器生成收敛到H的无约束局部极小值的轨迹。存在性问题在于：如果给定环境中存在这样的轨迹，则也存在一个缩放矩阵序列，使得算法1生成的轨迹是最优的。我们并未找到这样的序列，这仍然是一个有趣的开放问题。相反，我们证明了存在性问题的肯定结果。

定理3 如果 ∃{g_k} → x_unc^ ，其中每个车辆的{g_k}是收敛到H在给定x_0下的无约束局部最小值x_unc^ 的有效航路点序列，则 ∃{S_k} 使得 {x_k} → x_unc^*，其中 {x_k} 是由每个车辆使用算法1生成的轨迹序列。当且仅当对所有k满足 H(g_{k+1}) − H(g_k) < 0，g_k ∈ X_F，∀k，其中 X_F 为环境的整个可行区域，并且任意两个连续点 g_k、g_{k+1} 之间的步长满足假设1和车辆物理限制时，序列 {g_k} 是有效的。

证明 ：由命题2可知，对于所有k，必须满足 −∇H(x_k)^T d_k > 0。由(11)可知，为了满足此条件，需有 k_i > 0。由于 g_{k+1} − g_k ∈ R^p 且 S_k 的特征向量张成 R^p，因此可将 g_{k+1} − g_k = Σ_{i=1}^p a_i v_i，其中 a_i 为适当系数。又因对{g_k}的下降性要求，我们有 −∇H(x_k)^T (g_{k+1} − g_k) > 0，对所有k成立，故可选择 S_k 的一组标准正交基向量 v_i，使得 a_i > 0 且 f_i > 0 对所有i成立，其中 f_i 来自(9)，因此选择 k_i = s_k / (a_i f_i) 可满足 k_i > 0，对所有i成立，且由此得出

根据(10)中对 d_k 的定义，我们可以始终实现 d_k = g_{k+1} − g_k，对于该选择的k值，∀k均成立。由于 S_k 通过其特征向量和特征值完全确定为 S_k = V K V′，并且我们已经证明存在一个序列{S_k}，使得{d_k} = {g_{k+1} − g_k}，因此代理位置的相应序列{x_k}将达到H的无约束局部极小值，前提是{g_k}从给定的初始位置收敛到无约束局部最小值。□

4 结果

4.1 算法与仿真示例

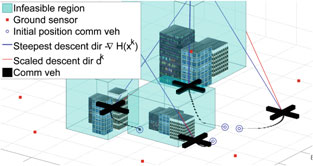
在本节中，我们总结了控制方法并给出了算法1，同时建议了一种启发式方法，用于为每辆飞行器选择合适的缩放矩阵 S_k。我们通过Matlab仿真展示了该算法以及寻找 S_k 的建议方法，仿真场景包括四辆通信车辆和八辆地面传感器车辆在三维空间中的情况（图3）。

算法1 优化通信的分布式控制（针对代理 i）

x_k = x_0, k = 0.
while k == 0 or ||x_{k+1} − x_k|| ≥ tol do
    k ← k + 1
    {根据环境拓扑计算缩放 S_k，参见算法2。}
    {使用智能体 i 的邻居计算梯度：} ∇_i H(x_k)
    {计算期望的航路点：} z_k ← x_k − s_k (S_k)^{-1} ∇_i H(x_k)
    {计算：} x̄_k^S ← （4）的解
    {计算满足假设1的可行步长 α_k}
    {计算新点 x_{k+1}，用于代理 i，使用步长 α_k:} x_{k+1} = x_k − α_k (x̄_k^S − x_k)。
end while

4.1.1 缩放矩阵 S_k 的启发式选择

我们建议一种为每辆车辆选择缩放矩阵 S_k 的可行方法，该方法易于实现，并且仅依赖于每个智能体局部的地图拓扑。通过仿真，我们展示了所得到的优化性能及其在智能体故障情况下的自适应能力。对于每个智能体，我们沿最速下降方向画一条线，在图 3a 中以蓝线表示，称此线为 g_L。设 O 为被 g_L 首次相交的不可行区域。我们希望计算 S_k，使得我们能够绕过 O，因此我们计算交点在 L 条边中的每一条上的投影，并选择使从当前位置 x_k 到边缘点 e^ 的弦具有最大的点积 −∇H(x_k)^T (e^ − x_k)。这表示一个尽可能接近最速下降方向但绕开阻碍该方向的不可行区域的方向。在图 3a中，对于每个其最速下降方向与不可行区域相交的车辆，该弦以红色绘制。

我们使用该弦来计算 S_k 的第一个特征向量，使得 v_1 = (e^ − x_k) / ||e^ − x_k||，然后 v_2 和 v_3 只需是彼此正交且与 v_1 正交的其他任意单位向量。

最后，我们可以设置特征值 k_2; k_3 ≫ k_1，以获得最接近 v_1 方向的下降方向 d_k，参见第3.2.1节和图3a中的讨论。然而我们提醒，若选择过大的特征值比例，将反过来影响收敛速度，因此在实际应用中不应使其超过必要程度。

随后，矩阵 S_k 通过其特征向量和特征值计算得到，即 S_k = V K V′，其中 V 和 K 在第3.2.1节中定义。如果对该车辆而言，方向 g_L 未被任何不可行区域阻挡，或不存在这样的边缘点 e^ 使得点积 −∇H(x_k)^T (e^ − x_k) > 0（这种情况表示没有任何绕行方向能在代价 H 上产生下降），则我们直接设 S_k = I，其中 I 是单位矩阵。

算法在2中进行了总结。对于图3中的仿真，我们设置 k_1 = 1；k_2 = 50；k_3 = 50，并在平均150次迭代中实现了满意的收敛，每次迭代在2.4 GHz CPU笔记本电脑上使用Matlab的CPLEX工具箱耗时约0.7秒。

4.1.2 关于何时使用缩放的讨论

缩放在远离阻碍路径的不可行区域时应用最为有效。由于任何下降方向 d_k 必须与负梯度方向的夹角小于90度，当车辆接近阻碍性不可行区域边缘时，能够避开该阻碍区域的下降方向范围会变小。因此，我们预计在障碍物之间距离较大的环境中，以及在算法2所述的检测到阻碍性障碍物时立即应用缩放的情况下，缩放的效果会更好。定理2表明，只要缩放矩阵 S_k 是严格正定的， x̄ k ≠ x_k，且 x_k 不是一个使得 ∇H(x_k) ≠ 0 的临界点，则所得方向 d_k 永远不会与负梯度方向垂直。为了直观理解，考虑二维情况以及由(10)式得到的未投影方向 d̃_k。当 S_k 的一个特征向量（例如 v_1）趋近于与 −∇H(x_k) 垂直时，负梯度在 v_1 方向上的分量趋近于零， f_1 → 0 且 −∇H(x_k) → f_2 v_2。因此方向 d̃_k = s_k (1/k_1 f_1 v_1 + 1/k_2 f_2 v_2) → s_k (1/k_2 f_2 v_2) 恰好是负梯度方向按 s_k / k_2 进行缩放后的结果。这意味着即使缩放应用不当（几乎与负梯度方向垂直），所得方向也永远不会完全垂直，实际上将与负梯度方向对齐；然而，如果 k_2 是一个非常大的数，则沿此方向的进展会变得非常缓慢，收敛速度受到影响，如第3.2.1节所讨论的那样。此外，如果当前位置处于一个驻点，此时投影 x̄_k 等于 x_k（这种情况可能出现在障碍物侧面，或代价函数的临界点处，其中 −∇H(x_k) = 0），那么即使施加了非零缩放，所得方向仍为零。这一点可以从更新方程 x {k+1} = x_k + α_k d_k 中直接看出，其中 d_k = (x̄_k − x_k)，若 x_k 是平稳的，则该项为零；或者在自由空间中，d_k = −s_k (S_k)^{-1} ∇H(x_k) = 0，在临界点处 ∇H(x_k) = 0，该项也为零。因此可以得出以下观察结论：(1) d_k 永远不会与最速下降方向垂直（实际上，当缩放方向垂直于负梯度方向时，所得方向会趋近于最速下降方向）；(2) 方向 d_k 在驻点或临界点处为零，因此即使使用正定缩放矩阵 S_k ≠ I，该方法也会停止；最后，(3) 缩放在距离阻碍路径的不可行区域较远时更为有效。基于这些观察，我们建议对车辆感知半径内任何阻碍路径的不可行区域都应用缩放。

4.2 硬件实验

该算法在包含两架移动四旋翼直升机和三个固定地面传感器的去中心化硬件实验中得到了验证。此次评估是在一个已知的具有障碍物的无GPS室内环境中进行的（麻省理工学院施塔塔中心的二楼中庭）。硬件平台由Ascending Technologies Pelican四旋翼飞行器组成，每架配备Hokuyo UTM-30LX激光测距仪和1.6GHz Intel Atom处理器（详情见[17]）。每架飞行器执行机载状态估计和控制，实现完全自主飞行。出于实际目的，每架四旋翼飞行器通过WiFi与相应的地面站笔记本电脑通信，人类输入和规划过程在地面站运行。移动飞行器与地面传感器之间的通信通道是模拟的。环境和车辆如图1所示。

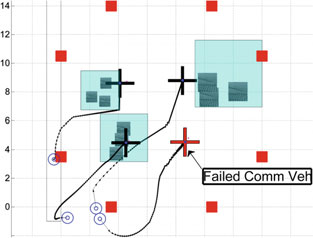
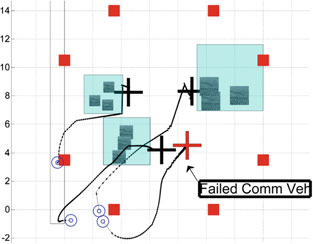
进行了十次试验，每次均从图4中所示的初始构型（x_0 V1；x_0 V2）开始，分别对应飞行器1和2。障碍物位置以粉色叠加在栅格地图上，实线轮廓表示构型空间边界，即不可行区域。这些区域并不妨碍通信，而是代表不安全或不可通过区域。在此环境中，这些障碍物包括一个开放式楼梯、一堵薄墙和一张桌子。四旋翼飞行器共享实时位姿信息，并在每次控制迭代中以10赫兹的频率根据算法1计算它们的下一个航路点。控制指令由航路点执行器人为限制为1赫兹。图4显示了每次试验中各车辆的轨迹以及它们收敛到的局部极小值构型。注意，车辆1绕过了墙。车辆2最初向墙移动，然后收敛到位于传感器1和3与车辆1之间的障碍物边界上的某一点。所有试验的平均持续时间为65秒，直到收敛。

的俯视图。障碍物（粉色）和构型空间边界（实线）叠加在环境的栅格地图上。固定地面传感器 (x_S1; x_S2; x_S3) 以红色方块表示。两条四旋翼飞行器轨迹以蓝绿色和黄色显示，初始位置（x_0 V1; x_0 V2）和最终位置（x_f V1; x_f V2）由蓝色方块标出。b 10次试验的平均试验成本及标准差)

5 讨论

我们提出了一种利用先前工作[5]中的通信代价函数，在存在不可行区域的环境中对异构空中和地面车辆网络进行通信优化的方法。未来的工作将致力于推广到一般的非光滑情况，并研究障碍物对通信强度的影响。我们通过理论分析以及仿真和硬件实验，证明了使用一系列缩放矩阵的有效性，该方法可通过沿避免不可行区域的轨迹运动，改善收敛解的范围。