拓扑排序_拓扑排序力扣-优快云博客

一，有向图拓扑排序

力扣 210. 课程表 II（DFS）

OpenJ_Bailian - 4084 拓扑排序（BFS）

一，有向图拓扑排序

有向无环图的拓扑排序是指给所有节点排序，使得所有的有向边都是从序号小的节点指向序号大的。

深度优先搜索和广度优先搜索都可以用于产生拓扑排序。

PS：不需要指定起点，算法自动寻找入度为0的点作为起点。起点可能不止1个，即使起点唯一，拓扑排序的结果也可能有很多种。

//有向图拓扑排序
class DirectedTopoSort :public KosarajuStrongConnect
{
public:
	//有向无环图拓扑排序，输入n=3，g.edges={{0,1}{0,2}{1,2}}, 输出{0,1,2}，有环则输出为空
	static vector<int> topoSortNoCircle(int n, DirectedGraphData<int>& g)
	{
		auto& v = g.edges;
		priority_queue<int, vector<int>, greater<int>> q;
		map<int, int>m;
		for (auto &vi : v)m[vi.b]++;
		for (int i = 0; i < n; i++)if (m[i] == 0)q.push(i);
		vector<int>ans;
		auto &mv = g.adjaList;
		while (!q.empty()) {
			int k = q.top();
			q.pop();
			ans.push_back(k);
			for (auto i : mv[k]) {
				m[i]--;
				if (m[i] == 0)q.push(i);
			}
		}
		return ans.size() == n ? ans : vector<int>{};
	}
	//有向图拓扑排序
	static vector<vector<int>> topoSort(DirectedGraphData<int>& g)
	{
		vector<vector<int>> con = connectComponent(g.adjaList);
		map<int, vector<int>> pointGraph = getPointGraph(con, g.adjaList);
		DirectedGraphData<int>ga(pointGraph);
		vector<int> vp = topoSortNoCircle(con.size(), ga);
		vector<vector<int>>ans;
		for (auto id : vp)ans.push_back(con[id]);
		return ans;
	}
};

力扣 210. 课程表 II（DFS）

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

示例 1:

输入: 2, [[1,0]]
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
示例 2:

输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
说明:

输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
提示:

1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
所有[ai, bi] 互不相同

class Solution {
public:
	void findOrder(vector<vector<int>>& diag, int loc, vector<int>& ans)
	{
		if (outNum[loc] || flag[loc])return;
		ans.push_back(loc);
		flag[loc]++;
		for (int i = 0; i < diag[loc].size(); i++)
		{
			outNum[diag[loc][i]]--;
			findOrder(diag, diag[loc][i], ans);
		}
	}
	vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
		vector<int>tmp;
		map<int, vector<int>>m;
		vector<vector<int>>diag;
		for (int i = 0; i < numCourses; i++)
		{
			diag.insert(diag.end(), tmp);
			visitt[i] = 0, outNum[i] = 0, flag[i] = 0;
		}
		for (int i = 0; i < prerequisites.size(); i++)
		{
			diag[prerequisites[i][1]].push_back(prerequisites[i][0]);
			m[prerequisites[i][1]].push_back(prerequisites[i][0]);
			outNum[prerequisites[i][0]]++;
		}
		if (HasDirectedCircle(numCourses, m))return tmp;
		vector<int>ans;
		flag.clear();
		for (int i = 0; i < numCourses; i++)
		{
			findOrder(diag, i, ans);
		}
		return ans;
	}
private:
	map<int, int>visitt;//单次访问标记
	map<int, int>flag;//所有访问标记
	map<int, int>inNum;//入度
	map<int, int>outNum;//出度
};

OpenJ_Bailian - 4084 拓扑排序（BFS）

给出一个图的结构，输出其拓扑排序序列，要求在同等条件下，编号小的顶点在前。

Input

若干行整数，第一行有2个数，分别为顶点数v和弧数a，接下来有a行，每一行有2个数，分别是该条弧所关联的两个顶点编号。
v<=100, a<=500

Output

若干个空格隔开的顶点构成的序列(用小写字母)。

Sample

Inputcopy	Outputcopy
6 8 1 2 1 3 1 4 3 2 3 5 4 5 6 4 6 5	v1 v3 v2 v6 v4 v5

注意这题输出的顺序，要输出所有拓扑排序的最小字典序的那个。

#include <iostream>
#include <string>
#include <vector>
#include <string.h>
#include <map>
#include <queue>
using namespace std;


//输入有向边集{{1，2}{1，3}{2，3}}，输出邻接表{1:{2,3},2:{3}}
map<int, vector<int>> edgeToAdjaList(const vector<vector<int>>& v)
{
	map<int, vector<int>> ans;
	for (auto &vi : v) {
		ans[vi[0]].push_back(vi[1]);
	}
	return ans;
}
//拓扑排序 BFS版
//输入n=3，v={{0,1}{0,2}{1,2}}, 输出{0,1,2}，有环则输出为空
vector<int> TopoSort(int n, const vector<vector<int>>&v)
{
	priority_queue<int, vector<int>, greater<int>> q;
	map<int, int>m;
	for (auto vi : v)m[vi[1]]++;
	for (int i = 0; i < n; i++)if(m[i]==0)q.push(i);
	vector<int>ans;
	auto mv = edgeToAdjaList(v);
	while (!q.empty()) {
		int k = q.top();
		q.pop();
		ans.push_back(k);
		for (auto i : mv[k]) {
			m[i]--;
			if (m[i] == 0)q.push(i);
		}
	}
	return ans.size() == n ? ans : vector<int>{};
}

int main()
{
	//freopen("D:/in.txt", "r",stdin);
	int v, a, x, y;
	cin >> v >> a;
	vector<vector<int>> p;
	while (a--) {
		cin >> x >> y;
		p.push_back(vector<int>{x-1, y-1});
	}
	auto ans = TopoSort(v, p);
	for (int i = 0; i < ans.size(); i++)cout << "v" << ans[i]+1 << " ";
	cout << endl;
	return 0;
}

力扣 1462. 课程表 IV

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你必须先选 ai 课程。

有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。

先决条件也可以是间接的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。

你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。

返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

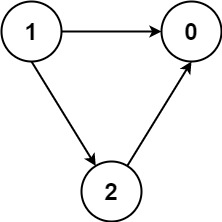
输入：numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

提示：

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
每一对 [ai, bi] 都不同
先修课程图中没有环。
1 <= queries.length <= 104
0 <= ui, vi <= n - 1
ui != vi

思路一：暴力bfs

class Solution {
public:
	vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
		vector<bool>ans;
		map<int, vector<int>>m;
		for (auto p : prerequisites)m[p[0]].push_back(p[1]);
		for (auto qi : queries)ans.push_back(checkIfPrerequisite(numCourses, m, qi[0], qi[1]));
		return ans;
	}
	bool checkIfPrerequisite(int n, map<int, vector<int>>p, int a,int b) {
		queue<int>q;
		q.push(a);
		map<int, int>m;
		while (!q.empty()) {
			int t = q.front();
			if (t == b)return true;
			q.pop();
			for (auto x : p[t])if (m[x] == 0) {
				m[x] = 1;
				q.push(x);
			}
		}
		return false;
	}
};

超时，很正常，有太多重复运算。

思路二：预处理，然后每次查询是O（1）的时间

预处理的方法是从所有入度为0的点开始dfs

class Solution {
public:
	vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
		map<int, vector<int>>m;
		map<int, int>isNotRoot;
		for (auto p : prerequisites)m[p[0]].push_back(p[1]), isNotRoot[p[1]] = 1;
		allPair.clear();
		for (int i = 0; i < n; i++)if (!isNotRoot[i]) {
			vector<int>v;
			dfs(i,m,v);
		}
		vector<bool>ans;
		for (auto q : queries)ans.push_back(allPair[q[0]][q[1]]);
		return ans;
	}
	void dfs(int r, map<int, vector<int>>&m,vector<int>&v) {
		for (auto x : v)allPair[x][r] = 1;
		v.push_back(r);
		for (auto x : m[r])dfs(x, m, v);
		v.erase(v.end() - 1);
	}
	map<int, map<int, int>>allPair;
};

超时，很正常，有太多重复运算。

思路三：预处理，然后每次查询是O（1）的时间

预处理的方法是拓扑排序，然后按照这个顺序遍历即可。

class Solution {
public:
	vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
		map<int, vector<int>>adjaList;
		map<int, vector<int>>fa;
		for (auto p : prerequisites)adjaList[p[0]].push_back(p[1]), fa[p[1]].push_back(p[0]);
		DirectedGraphData<int>g(adjaList);
		vector<int> tp = DirectedTopoSort::topoSortNoCircle(n, g);
		map<int, map<int,int>>fas;
		for (auto x : tp) {
			for (auto f : fa[x]) {
				fas[x][f] = 1;
				for (auto par : fas[f])fas[x][par.first] = 1;
			}
		}
		vector<bool>ans;
		for (auto q : queries)ans.push_back(fas[q[1]][q[0]]);
		return ans;
	}
};

LCR 114. 火星词典

现有一种使用英语字母的外星文语言，这门语言的字母顺序与英语顺序不同。

给定一个字符串列表 words ，作为这门语言的词典，words 中的字符串已经 按这门新语言的字母顺序进行了排序 。

请你根据该词典还原出此语言中已知的字母顺序，并 按字母递增顺序 排列。若不存在合法字母顺序，返回 "" 。若存在多种可能的合法字母顺序，返回其中 任意一种 顺序即可。

字符串 s 字典顺序小于 字符串 t 有两种情况：

在第一个不同字母处，如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前，那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同，那么 s.length < t.length 时，s 的字典顺序也小于 t 。

示例 1：

输入：words = ["wrt","wrf","er","ett","rftt"]
输出："wertf"

示例 2：

输入：words = ["z","x"]
输出："zx"

示例 3：

输入：words = ["z","x","z"]
输出：""
解释：不存在合法字母顺序，因此返回 "" 。

提示：

1 <= words.length <= 100
1 <= words[i].length <= 100
words[i] 仅由小写英文字母组成


class Solution {
public:
    string alienOrder(vector<string>& words) {
        map<char,int>m;
        map<int,char>m2;
        for(auto &s:words){
            for(auto c:s)if(m.find(c)==m.end())m[c]=m.size(),m2[m[c]]=c;
        }
        map<int, vector<int>> adjaList;
        for(int i=1;i<words.size();i++){
            auto v=cmp(words[i-1],words[i]);
            if(v.empty()){
                if(words[i-1].length()>words[i].length())return "";
                continue;
            }
            adjaList[m[v[0]]].push_back(m[v[1]]);
        }
        DirectedGraphData<int>g(adjaList);
        auto v=DirectedTopoSort::topoSortNoCircle(m.size(),g);
        string s="";
        for(auto vi:v)s+=m2[vi];
        return s;
    }
    vector<char>cmp(string&s1,string &s2){
        for(int i=0;i<s1.length()&&i<s2.length();i++){
            if(s1[i]!=s2[i])return vector<char>{s1[i],s2[i]};
        }
        return vector<char>{};
    }
};

二，无向图拓扑排序

无向无环图拓扑排序是指定节点作为根，把图变成多叉树（一个节点的不同子节点之间无法区分顺序）

	//无向拓扑排序，输入无向无环图{{1，2}{1，3}{4，3}}的邻接表和指定根1，输出父节点表{4:3, 3:1, 2:1}
	static map<int, int> undirectedEdgeToFatherList(map<int, vector<int>>& m, int root)
	{
		map<int, int>visit;
		map<int, int>fa;
		queue<int>q;
		q.push(root);
		visit[root] = 1;
		while (!q.empty()) {
			int id = q.front();
			q.pop();
			for (auto c : m[id]) {
				if (visit[c] == 0)q.push(c), fa[c] = id;
				visit[c] = 1;
			}
		}
		return fa;
	}

力扣 1377. T 秒后青蛙的位置

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
青蛙无法跳回已经访问过的顶点。
如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。

示例 1：

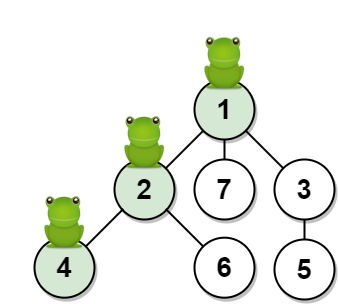
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4，因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。

示例 2：

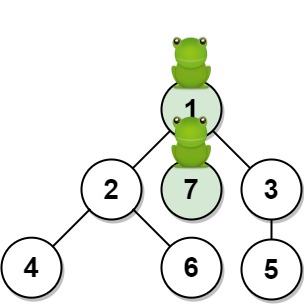
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出：0.3333333333333333
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。

提示：

1 <= n <= 100
edges.length == n - 1
edges[i].length == 2
1 <= ai, bi <= n
1 <= t <= 50
1 <= target <= n


class Solution {
public:
	double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
		map<int, vector<int>>m;
		for (auto v : edges) {
			m[v[0]].push_back(v[1]);
			m[v[1]].push_back(v[0]);
		}
		map<int, int>fa = UndirectedEdgeToFatherList(m, 1);
		m.clear();
		for (auto p : fa) {
			m[p.second].push_back(p.first);
		}
		stack<int>s;
		s.push(target);
		auto x = target;
		while (x != 1) {
			x = fa[x];
			s.push(x);
		}
		if (t < s.size() - 1)return 0;
		if (t > s.size() - 1 && !m[target].empty())return 0;
		double ans = 1;
		while (!s.empty()) {
			x = s.top();
			if (x == target)return ans;
			s.pop();
			ans /= m[x].size();
		}
		return 0;
	}
};

三，有向图的唯一拓扑排序

给定有向图，存在唯一的拓扑排序等价于，存在n-1条边把所有的n个节点连起来构成一条简单路径，且其他的边也满足对应的方向。

力扣 LCR 115. 序列重建

给定一个长度为 n 的整数数组 nums ，其中 nums 是范围为 [1，n] 的整数的排列。还提供了一个 2D 整数数组 sequences ，其中 sequences[i] 是 nums 的子序列。
检查 nums 是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列，并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences ，可能存在多个有效的 超序列 。

例如，对于 sequences = [[1,2],[1,3]] ，有两个最短的 超序列 ，[1,2,3] 和 [1,3,2] 。
而对于 sequences = [[1,2],[1,3],[1,2,3]] ，唯一可能的最短 超序列 是 [1,2,3] 。[1,2,3,4] 是可能的超序列，但不是最短的。

如果 nums 是序列的唯一最短 超序列 ，则返回 true ，否则返回 false 。
子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素，而不改变其余元素的顺序的序列。

示例 1：

输入：nums = [1,2,3], sequences = [[1,2],[1,3]]
输出：false
解释：有两种可能的超序列：[1,2,3]和[1,3,2]。
序列 [1,2] 是[1,2,3]和[1,3,2]的子序列。
序列 [1,3] 是[1,2,3]和[1,3,2]的子序列。
因为 nums 不是唯一最短的超序列，所以返回false。

示例 2：

输入：nums = [1,2,3], sequences = [[1,2]]
输出：false
解释：最短可能的超序列为 [1,2]。
序列 [1,2] 是它的子序列：[1,2]。
因为 nums 不是最短的超序列，所以返回false。

示例 3：

输入：nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]]
输出：true
解释：最短可能的超序列为[1,2,3]。
序列 [1,2] 是它的一个子序列：[1,2,3]。
序列 [1,3] 是它的一个子序列：[1,2,3]。
序列 [2,3] 是它的一个子序列：[1,2,3]。
因为 nums 是唯一最短的超序列，所以返回true。

提示：

n == nums.length
1 <= n <= 104
nums 是 [1, n] 范围内所有整数的排列
1 <= sequences.length <= 104
1 <= sequences[i].length <= 104
1 <= sum(sequences[i].length) <= 105
1 <= sequences[i][j] <= n
sequences 的所有数组都是唯一的
sequences[i] 是 nums 的一个子序列

use std::collections::HashMap;
impl Solution {
    pub fn sequence_reconstruction(nums: Vec<i32>, sequences: Vec<Vec<i32>>) -> bool {
        let mut m = HashMap::new();
        for v in sequences{
            for i in 1..v.len(){
                if m.get_mut(&(v[i-1],v[i])).is_none(){
                    m.insert((v[i-1],v[i]),1);
                }
            }
        }
        for i in 1..nums.len(){
            if m.get_mut(&(nums[i-1],nums[i])).is_none(){
                return false;
            }
        }
        return true;
    }
}