puzzle（0713）光学解锁

目录

光学解锁

第一章

第二章

光束总数理论

分光器的合并

第三章

---

光学解锁

apk下载

通过把箱子在限定区域内移动，使得目标都被照亮。

每个目标需要的光束数不一样，有1到3的。

有很多箱子是不能移动的，还有配对的箱子，是传送门。

第一章

1-5

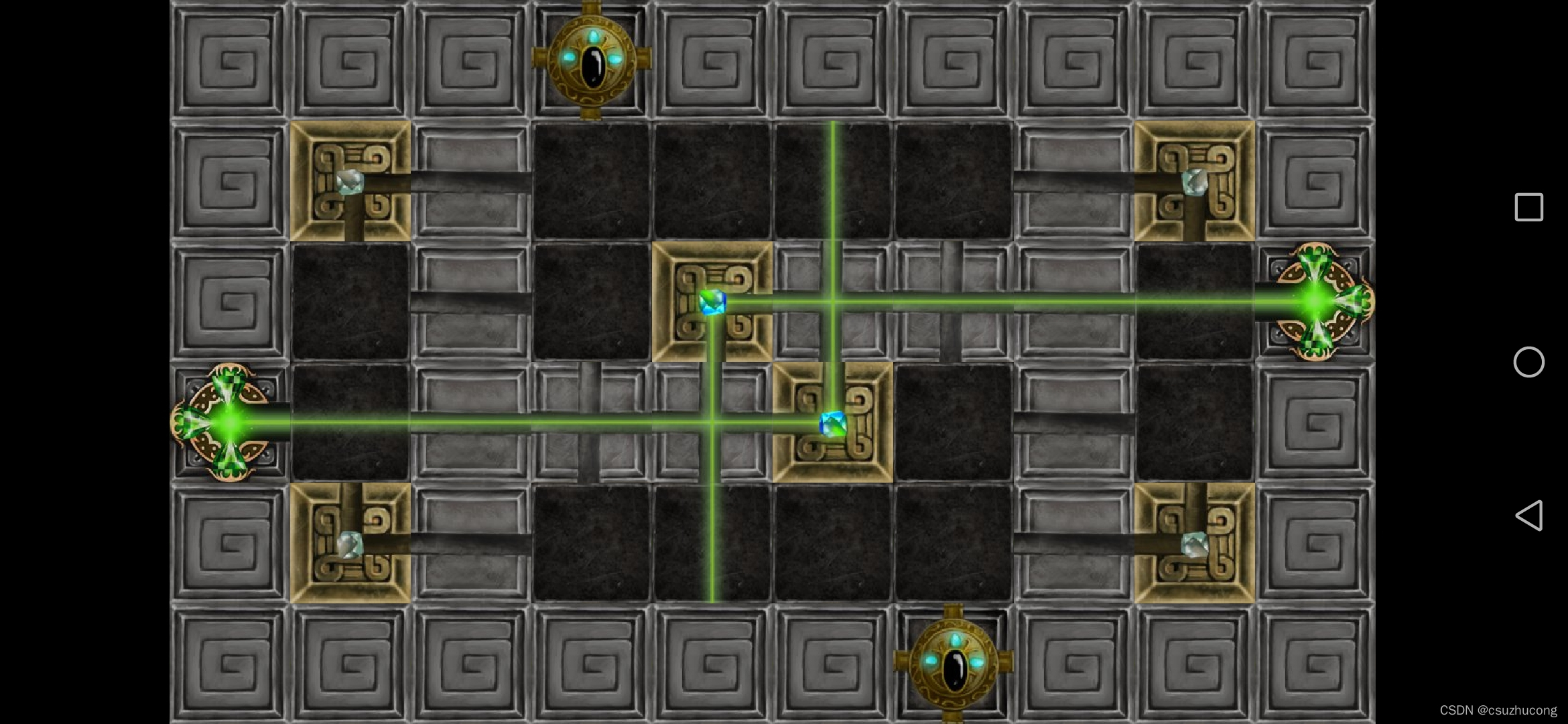
1-8

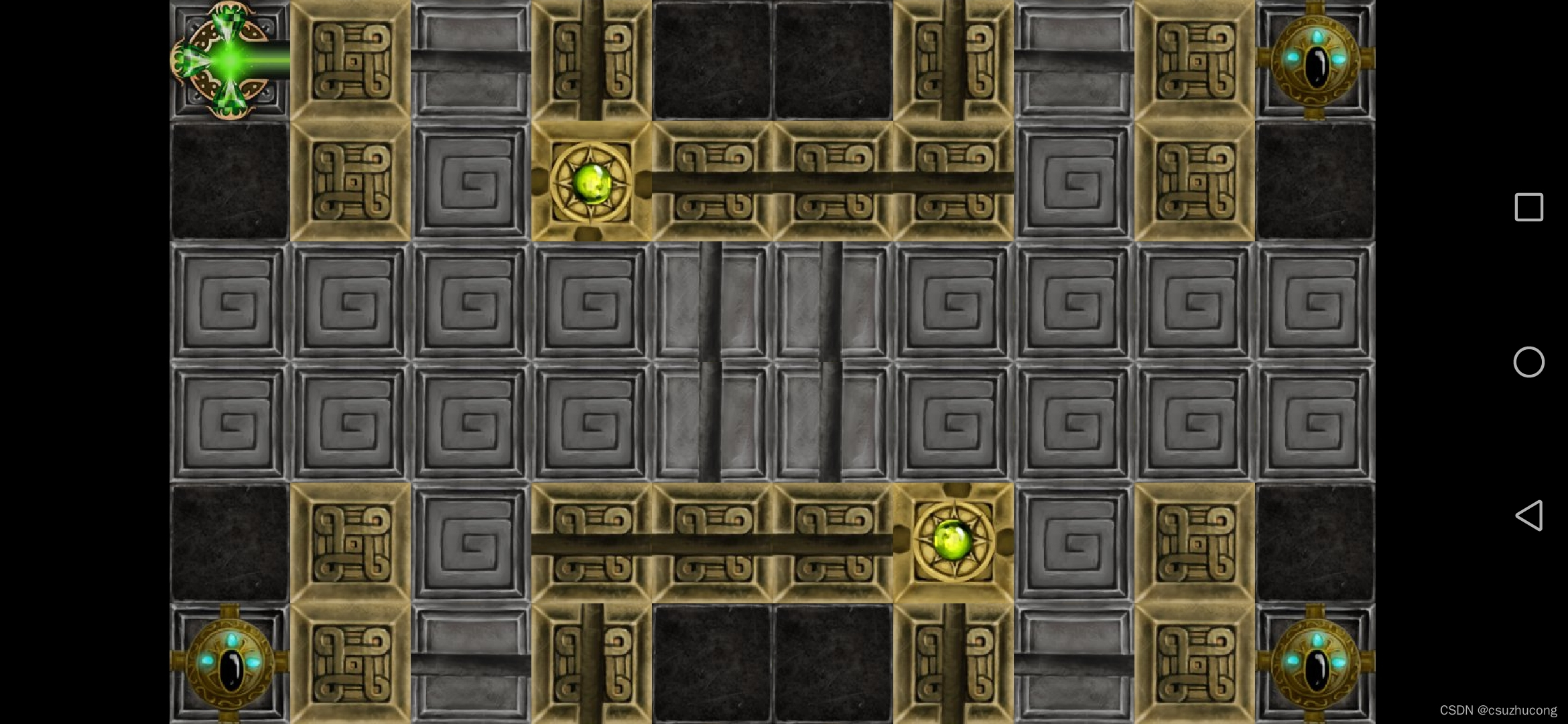
1-9

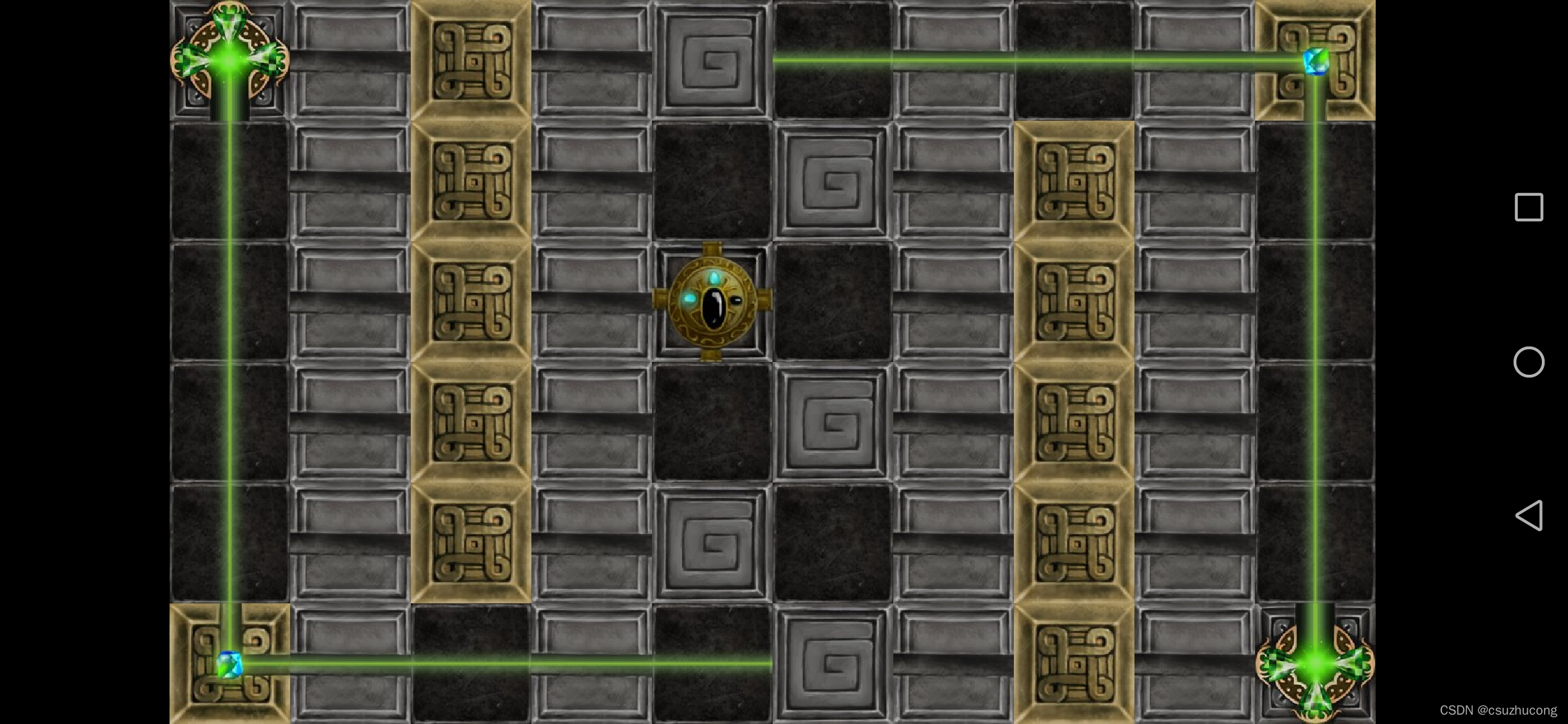
1-11

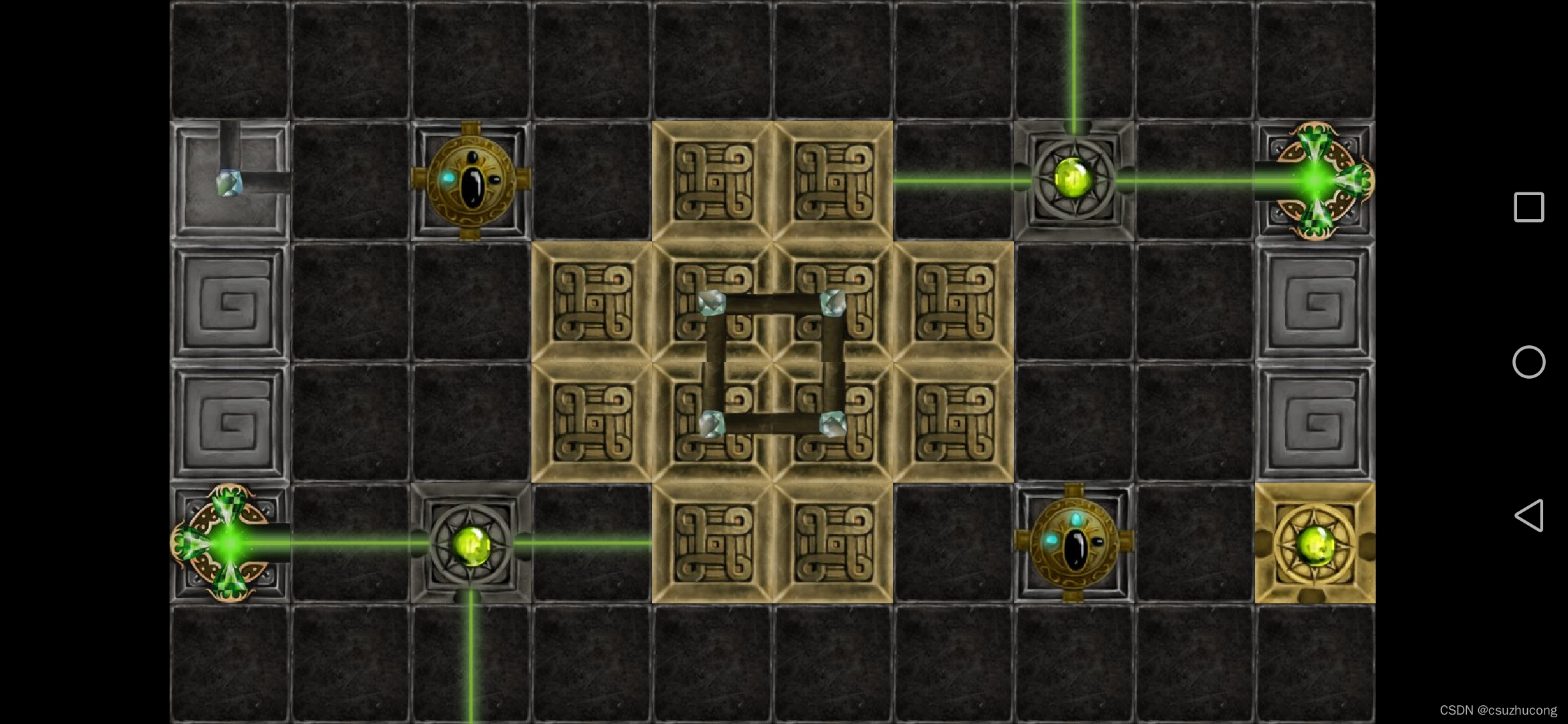
1-14

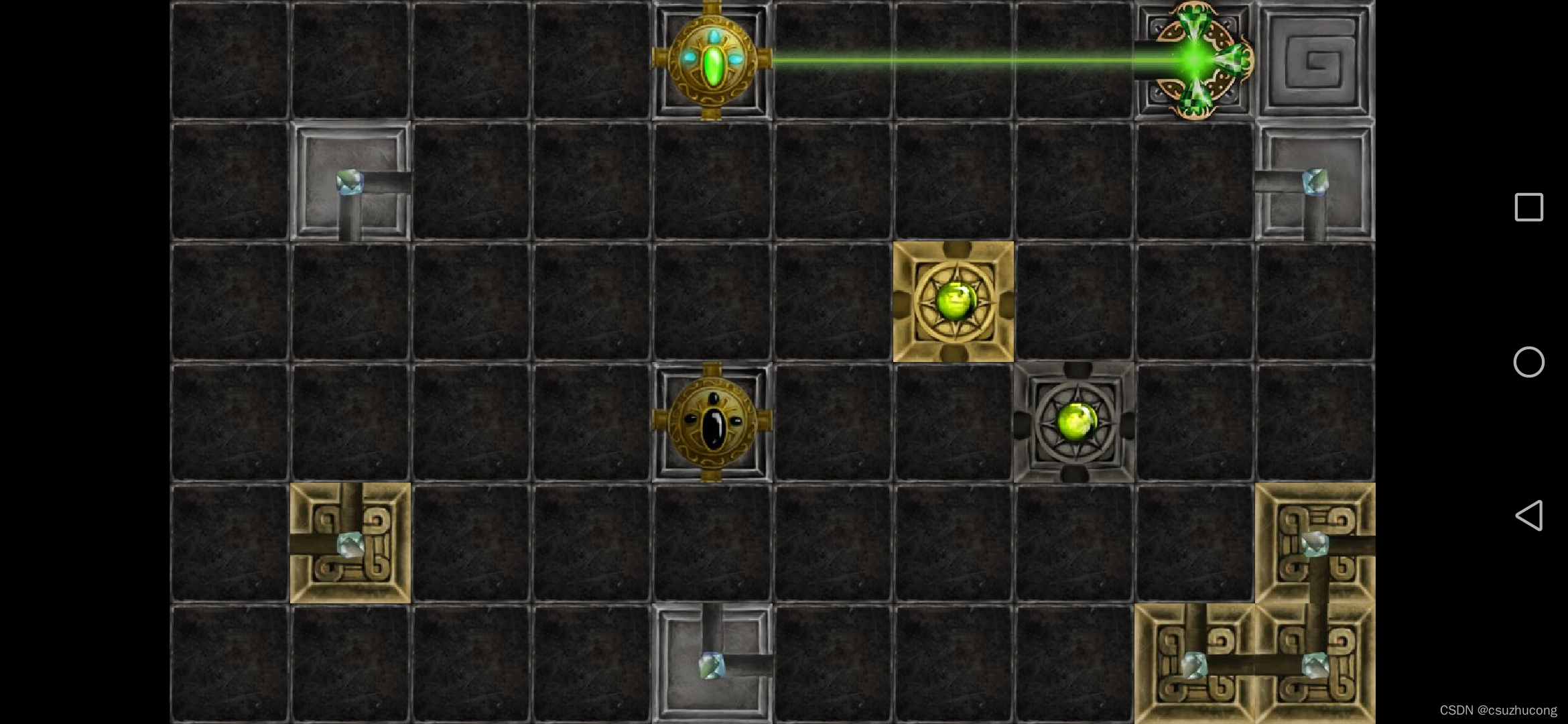
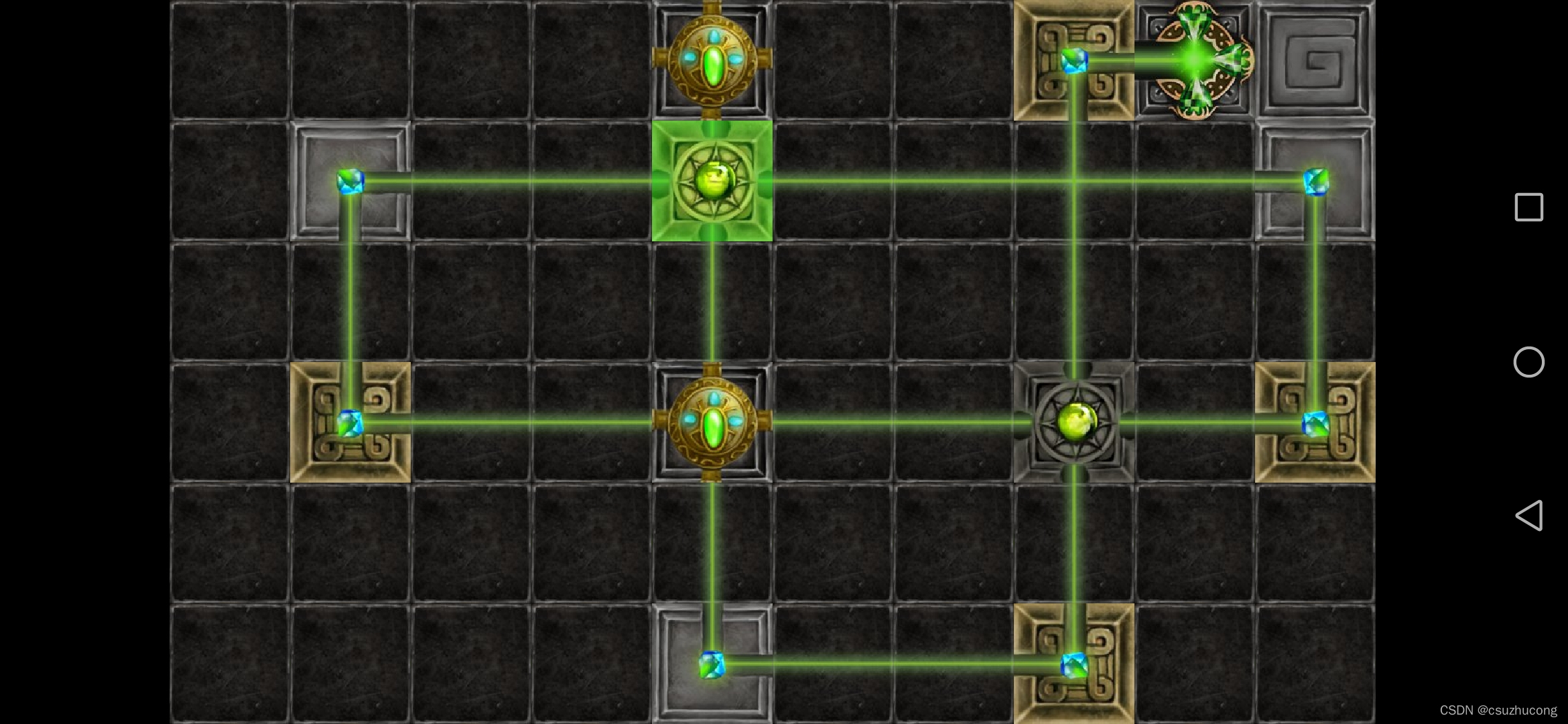
 1-17

 

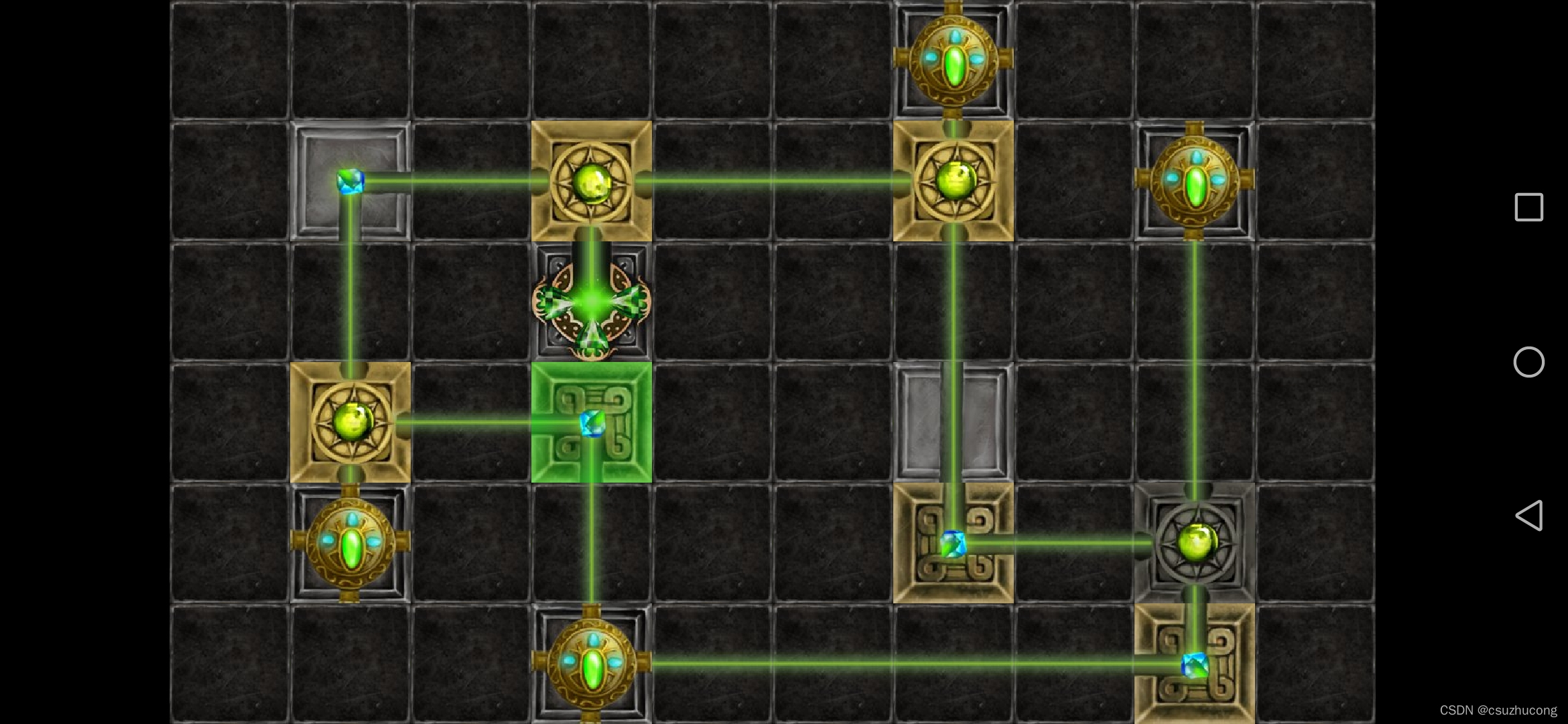
 1-18

这关比较简单

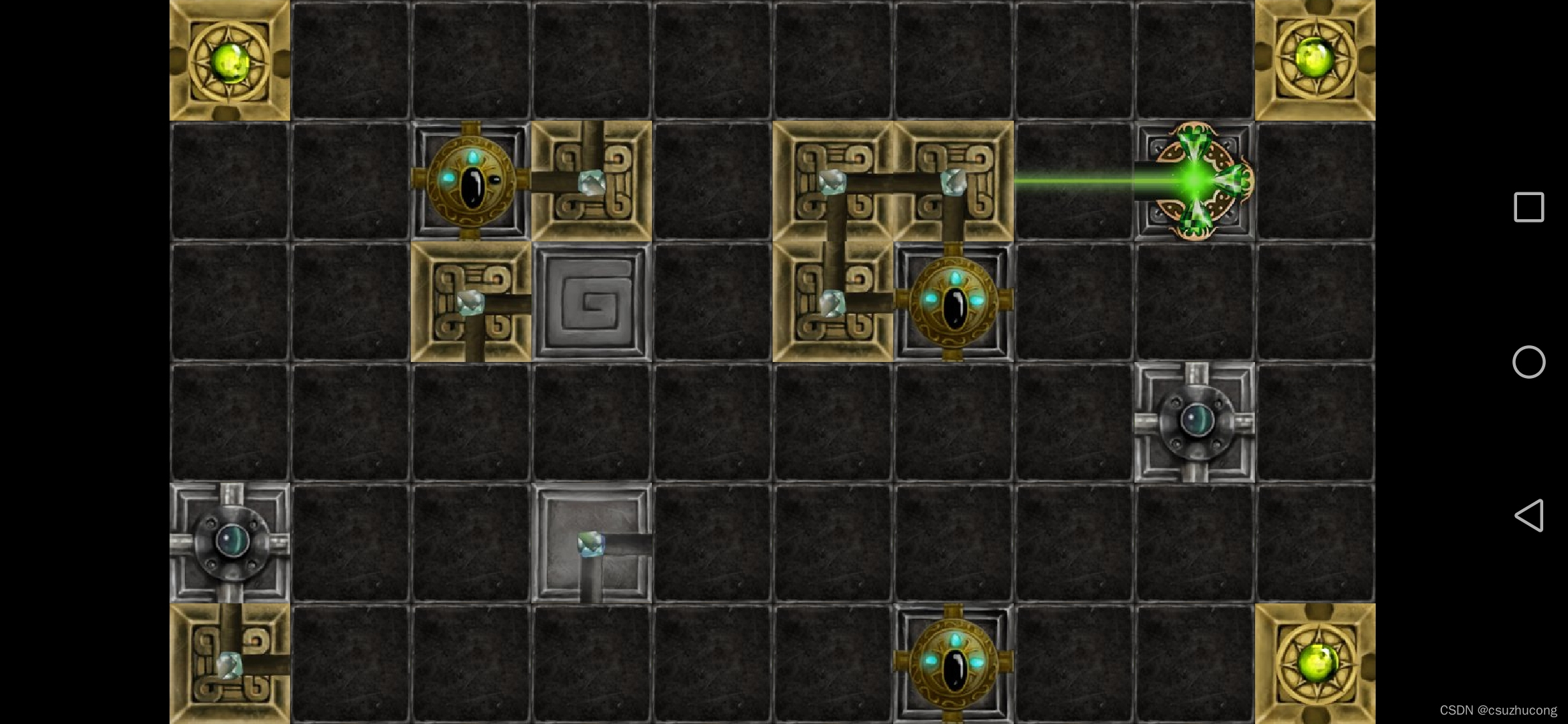
 1-19

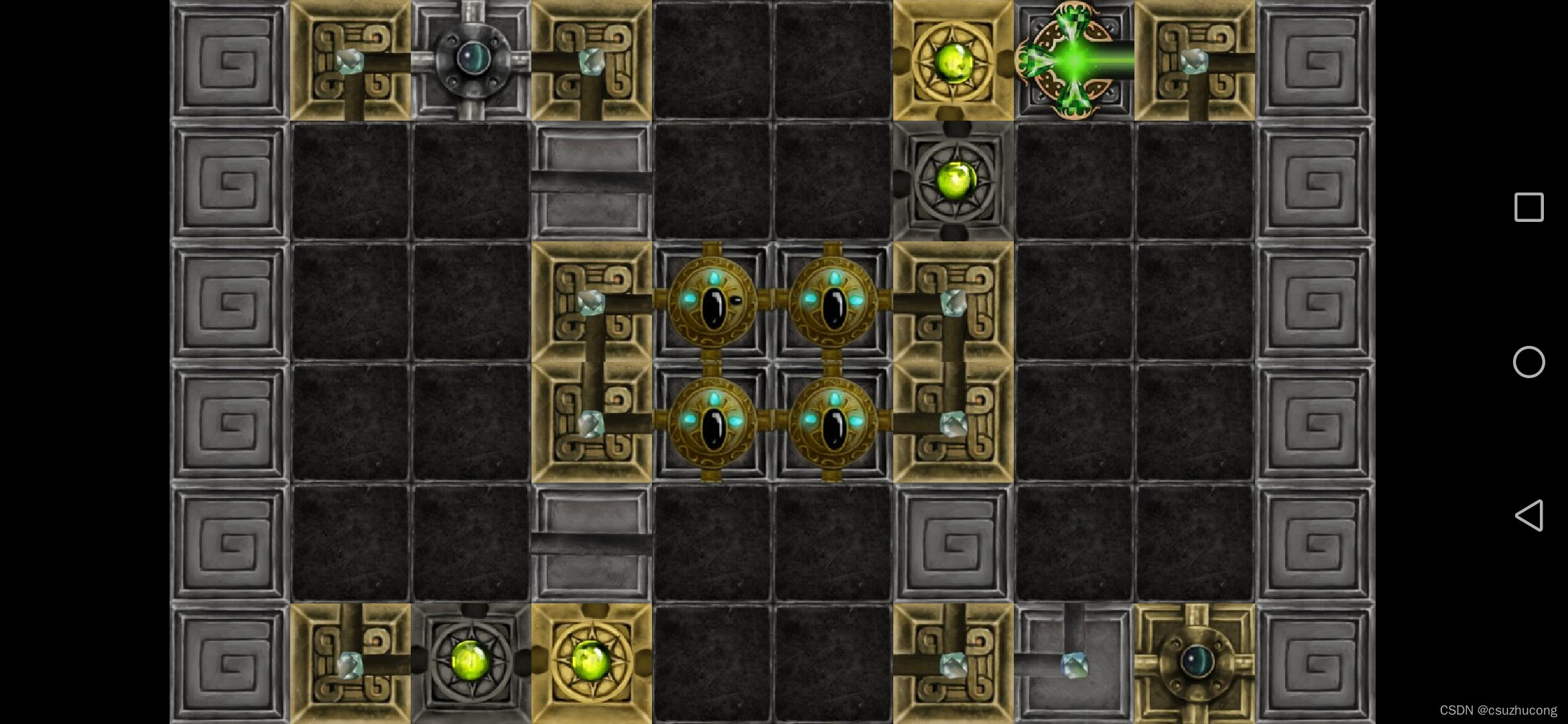
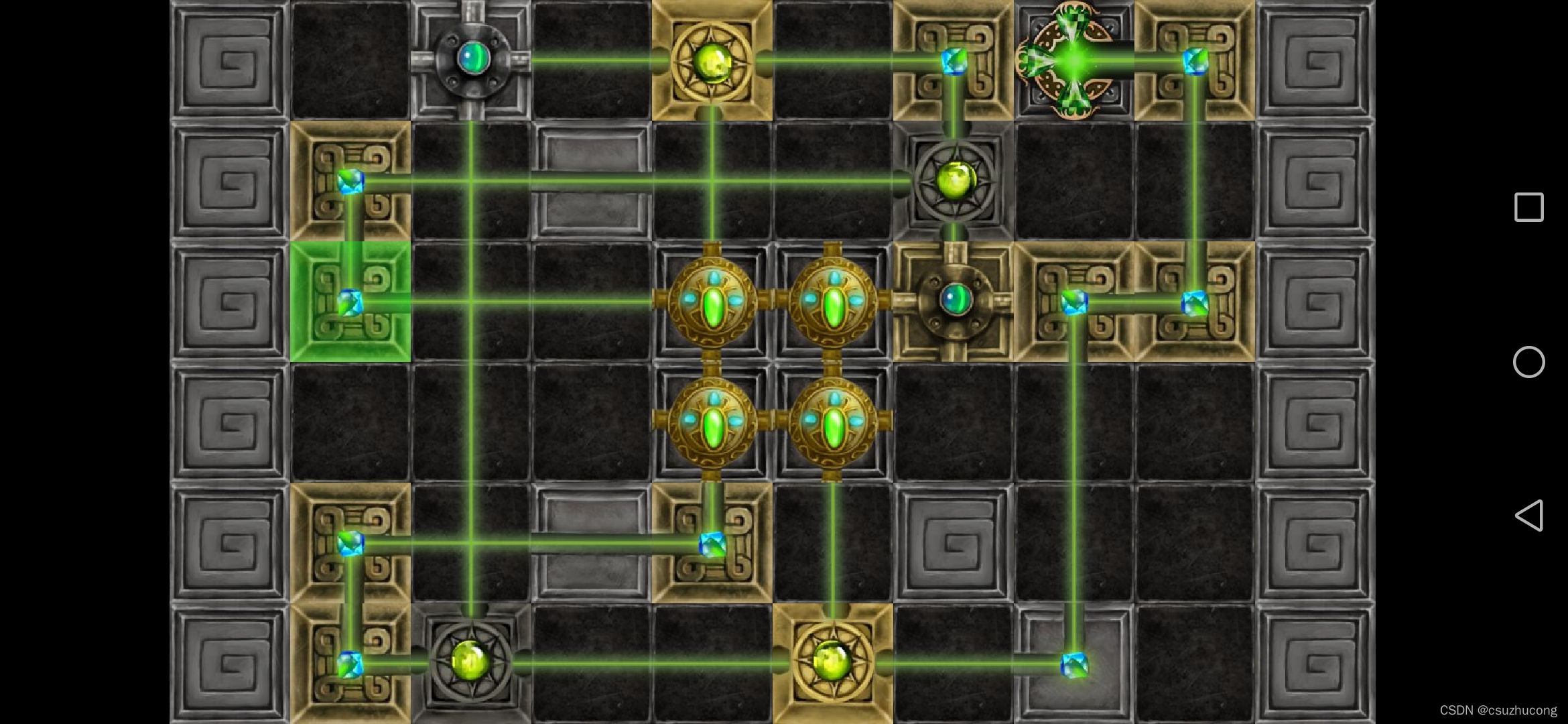
1-20

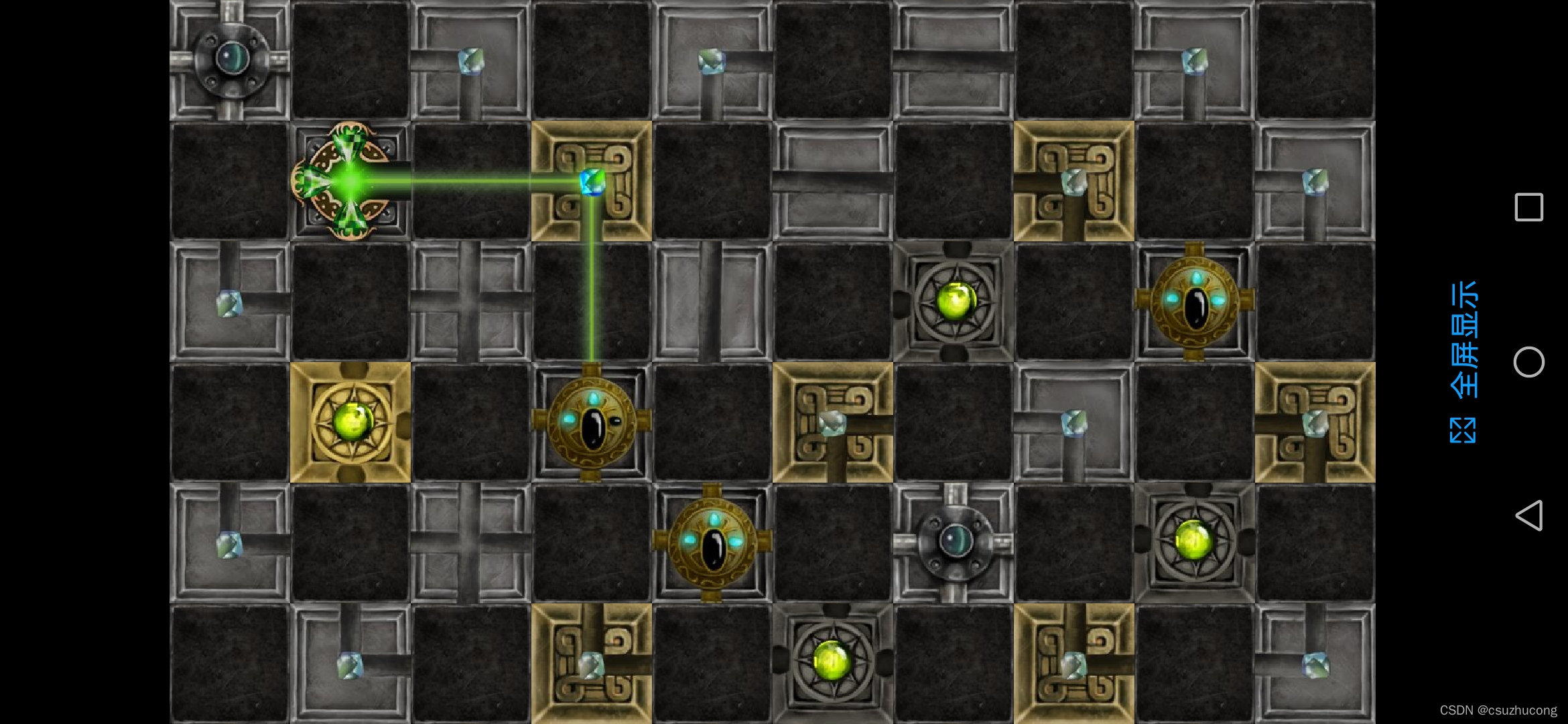
首先看左上角的可移动箱子的位置，如果放在第二行第三列的话是无解的：

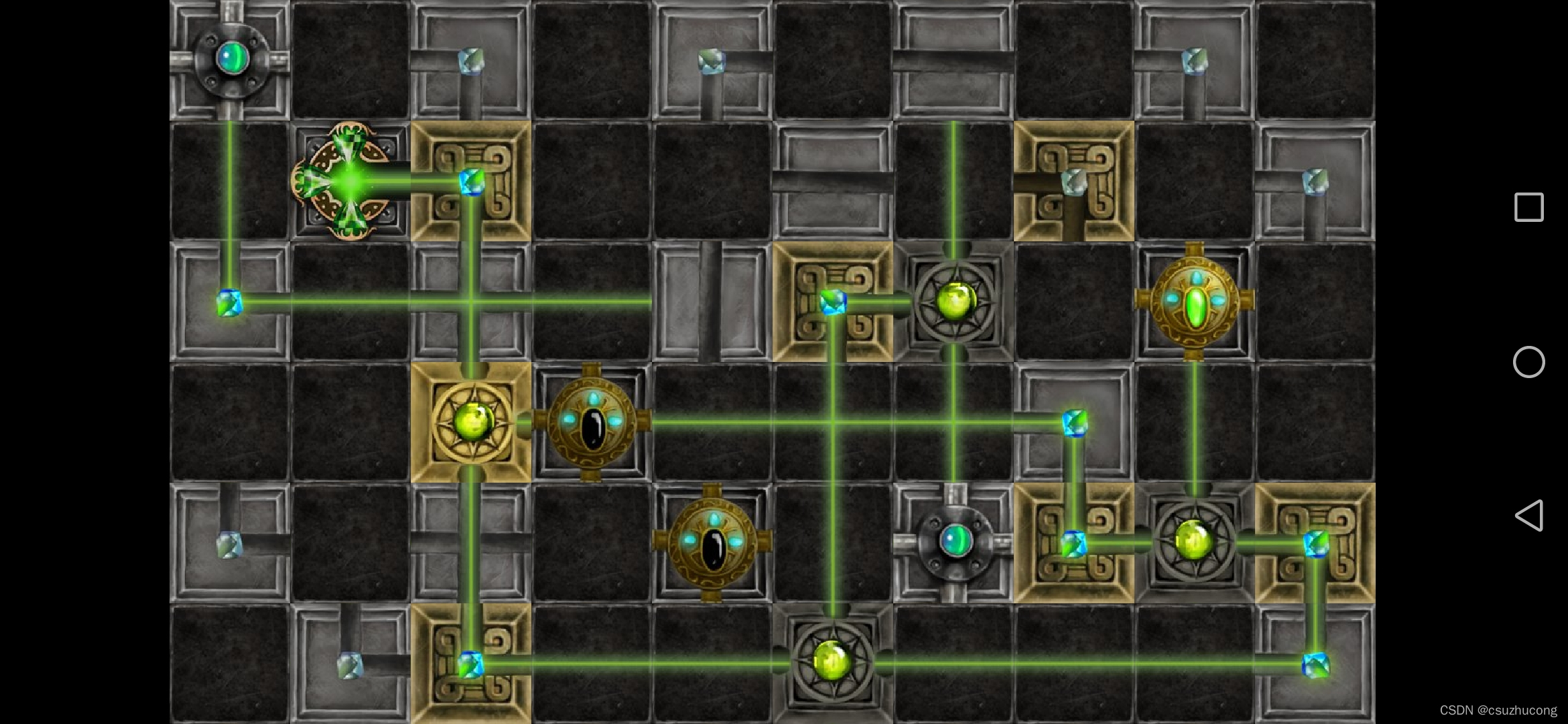
 所以这第一个箱子不能放在第二行，然后一步步推就可以得到答案了。

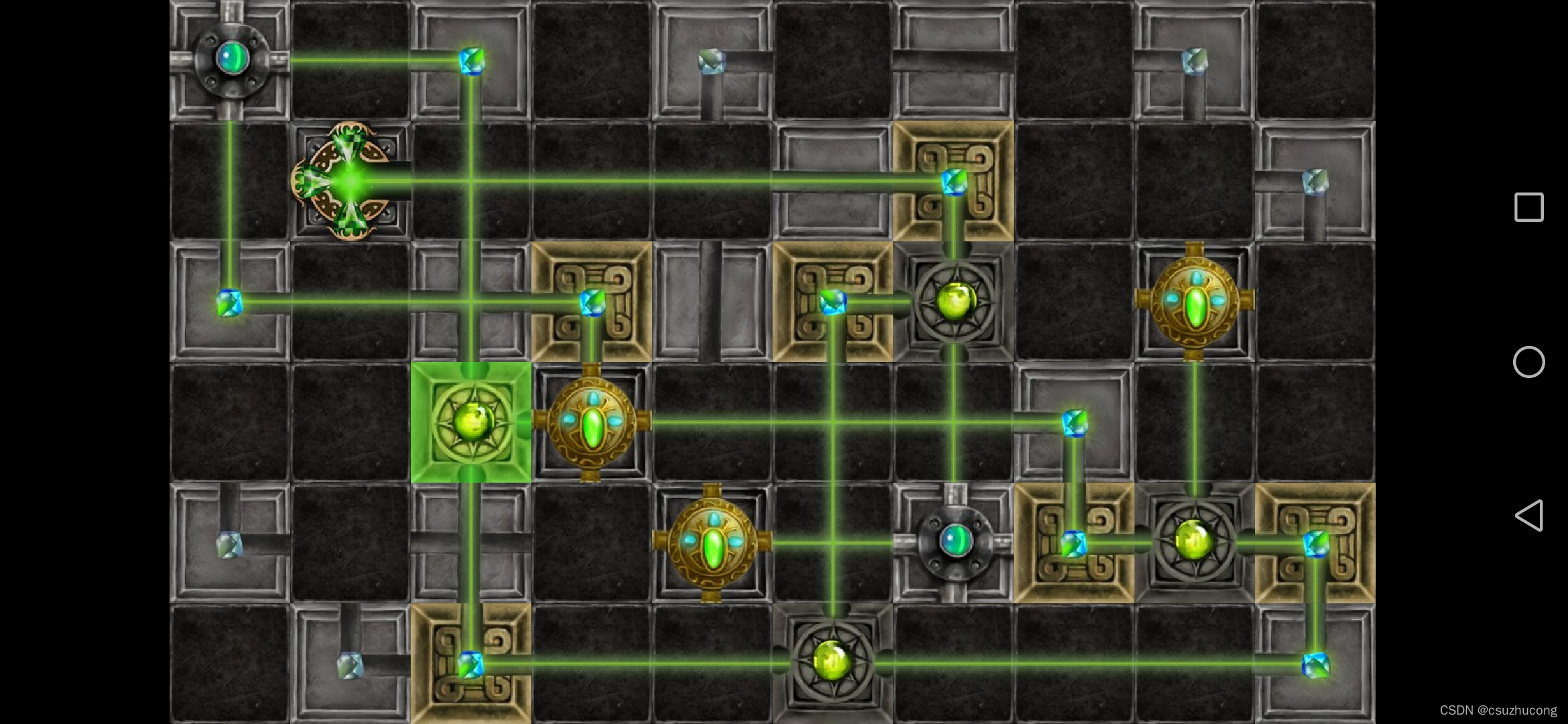
第二章

2-1

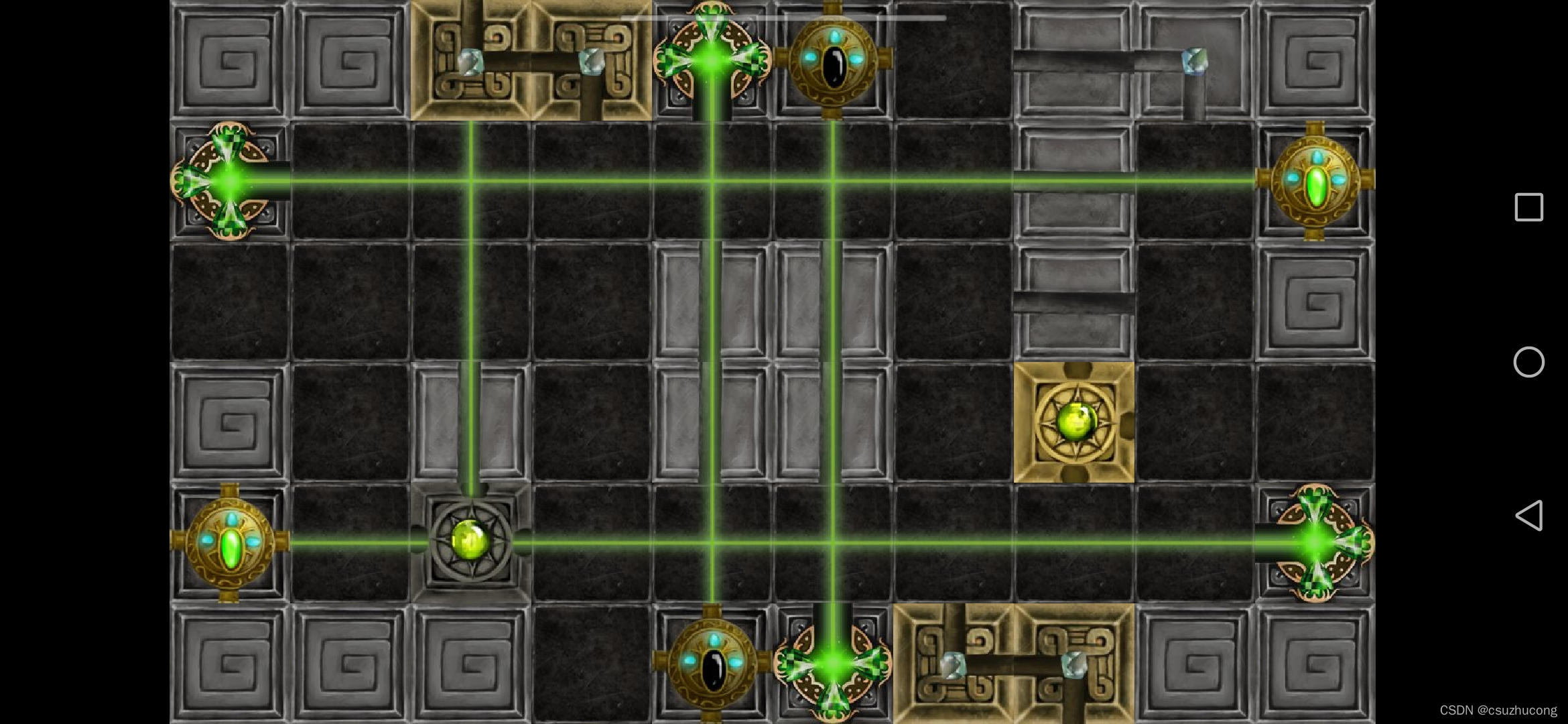
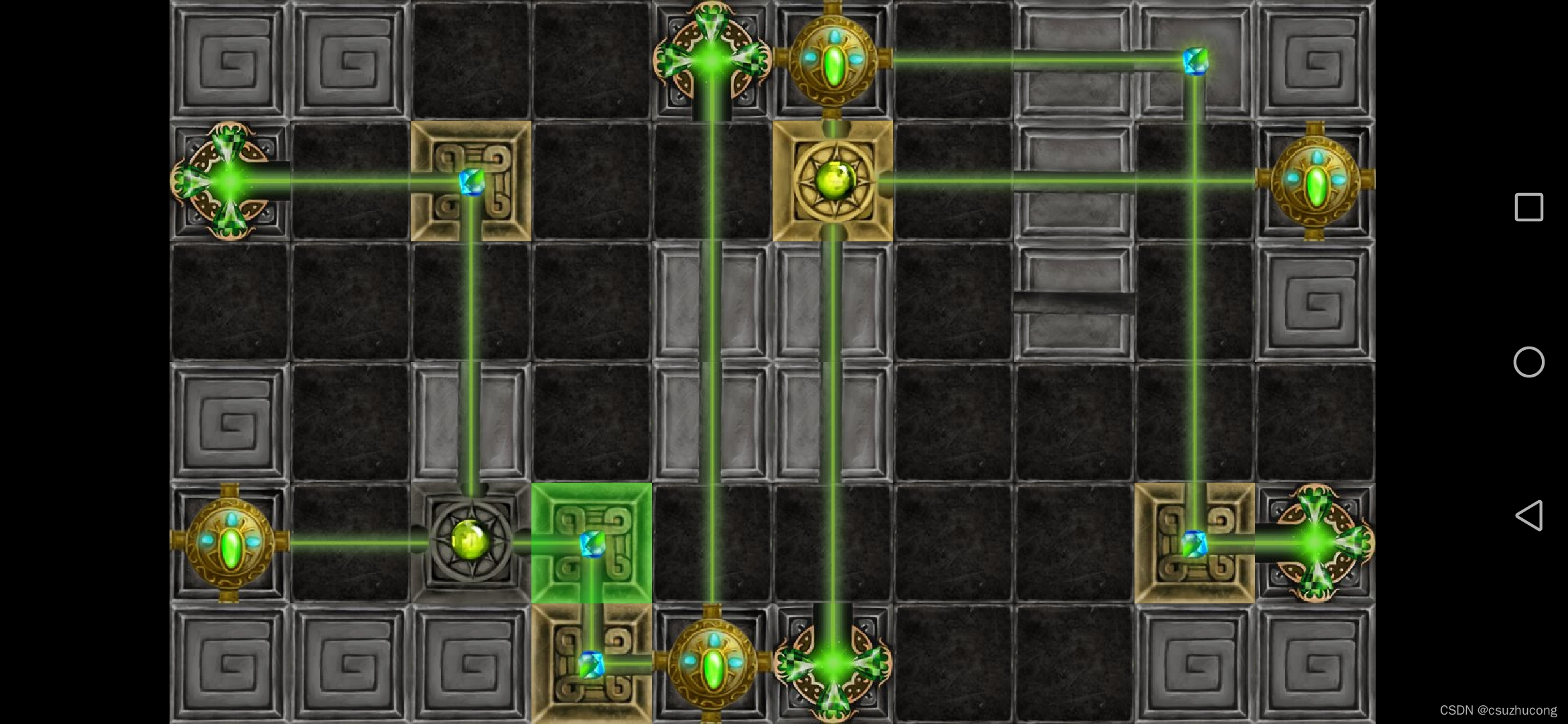
2-2

 

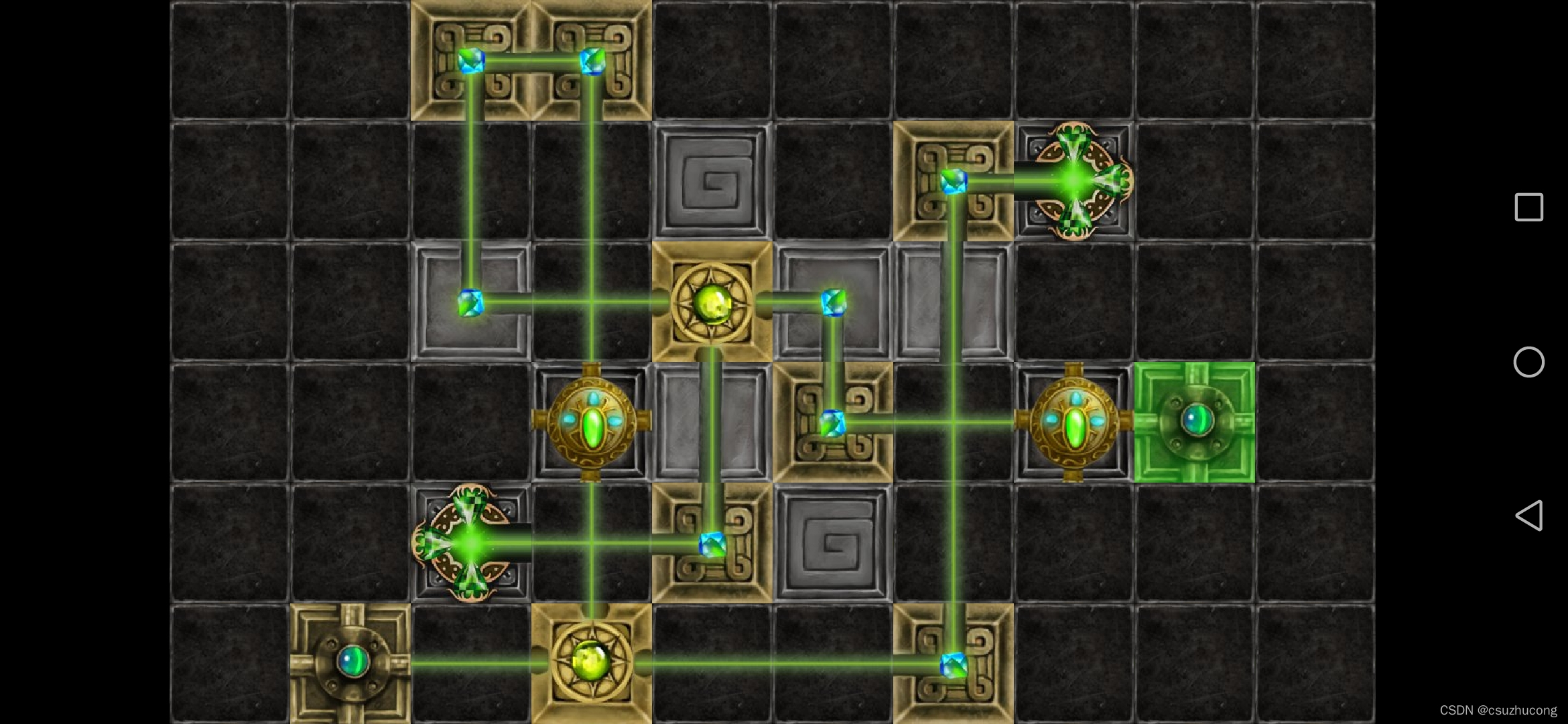
 2-3

 

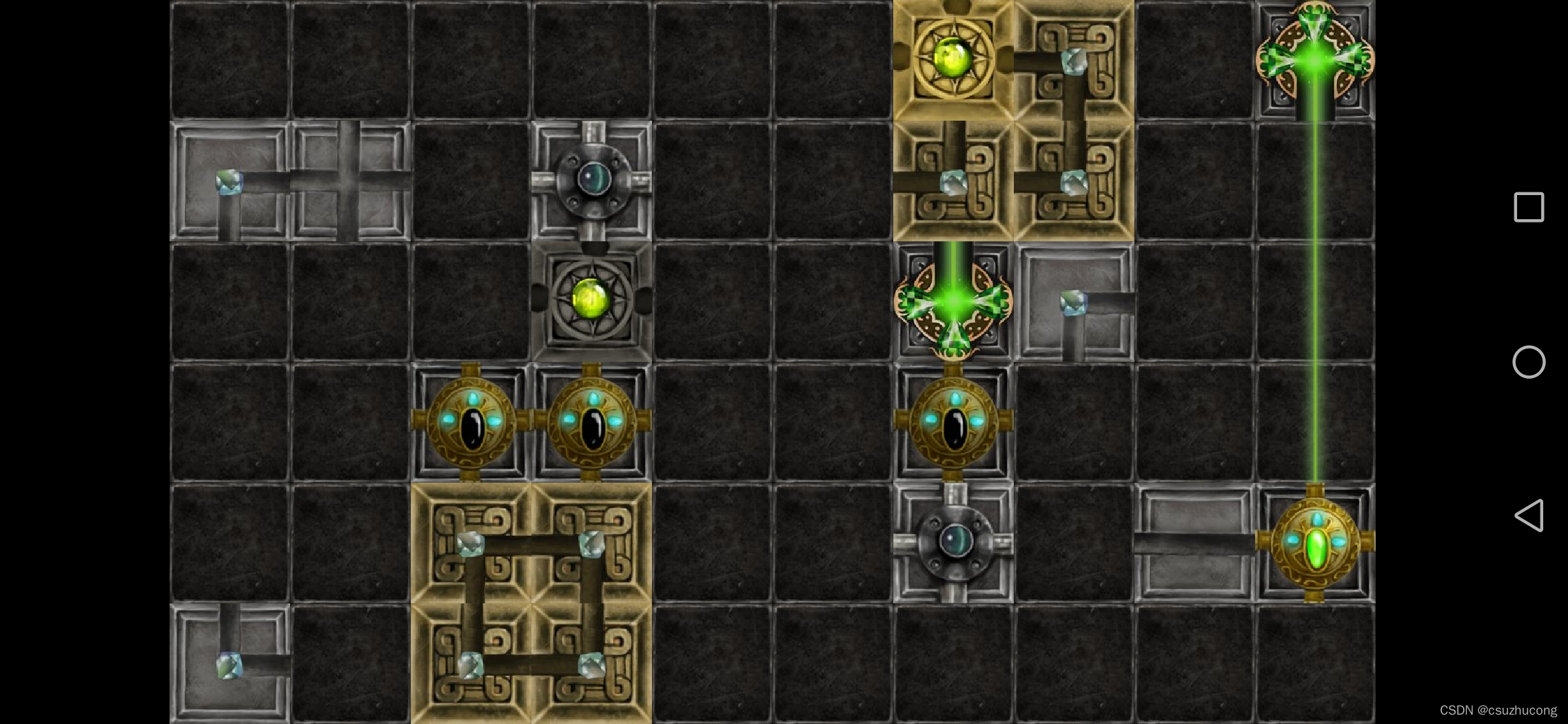
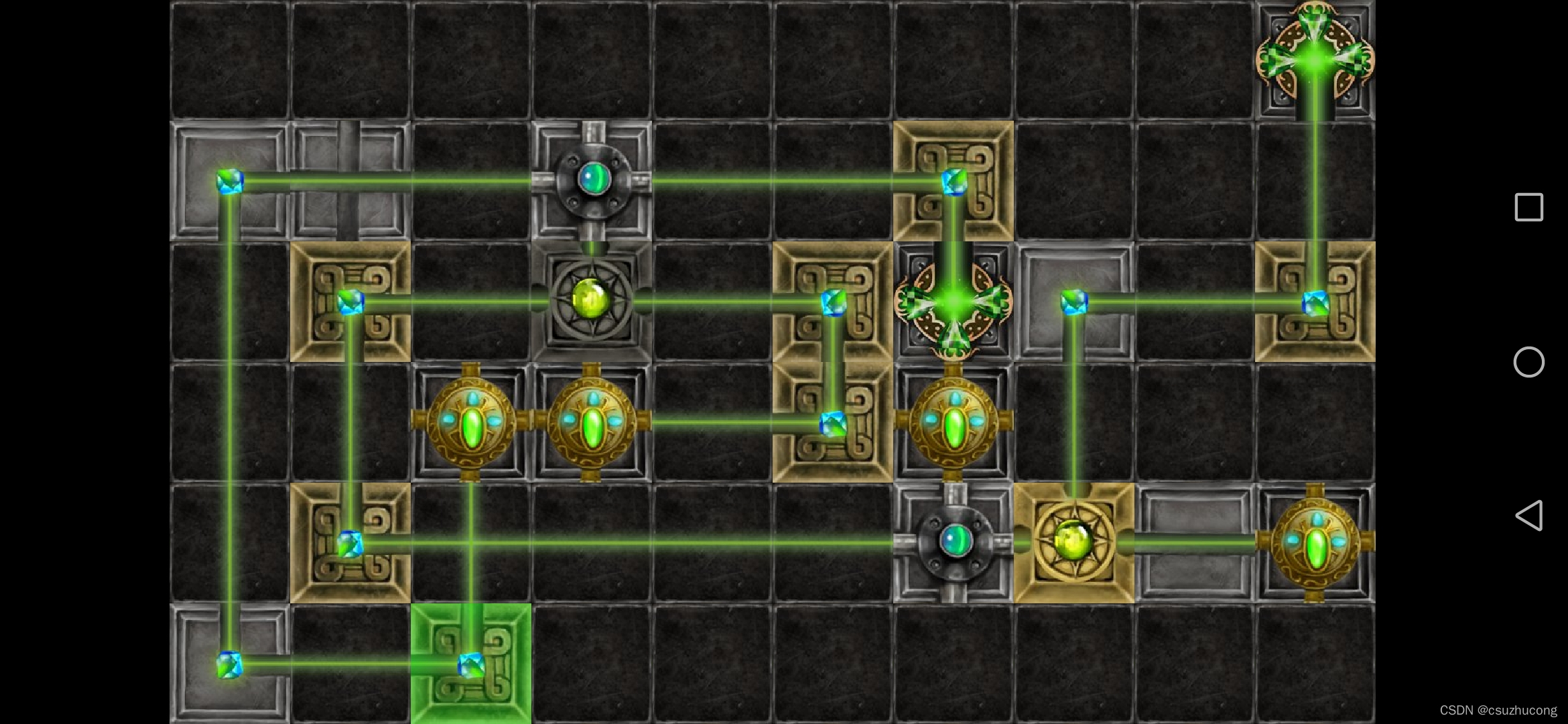
2-4

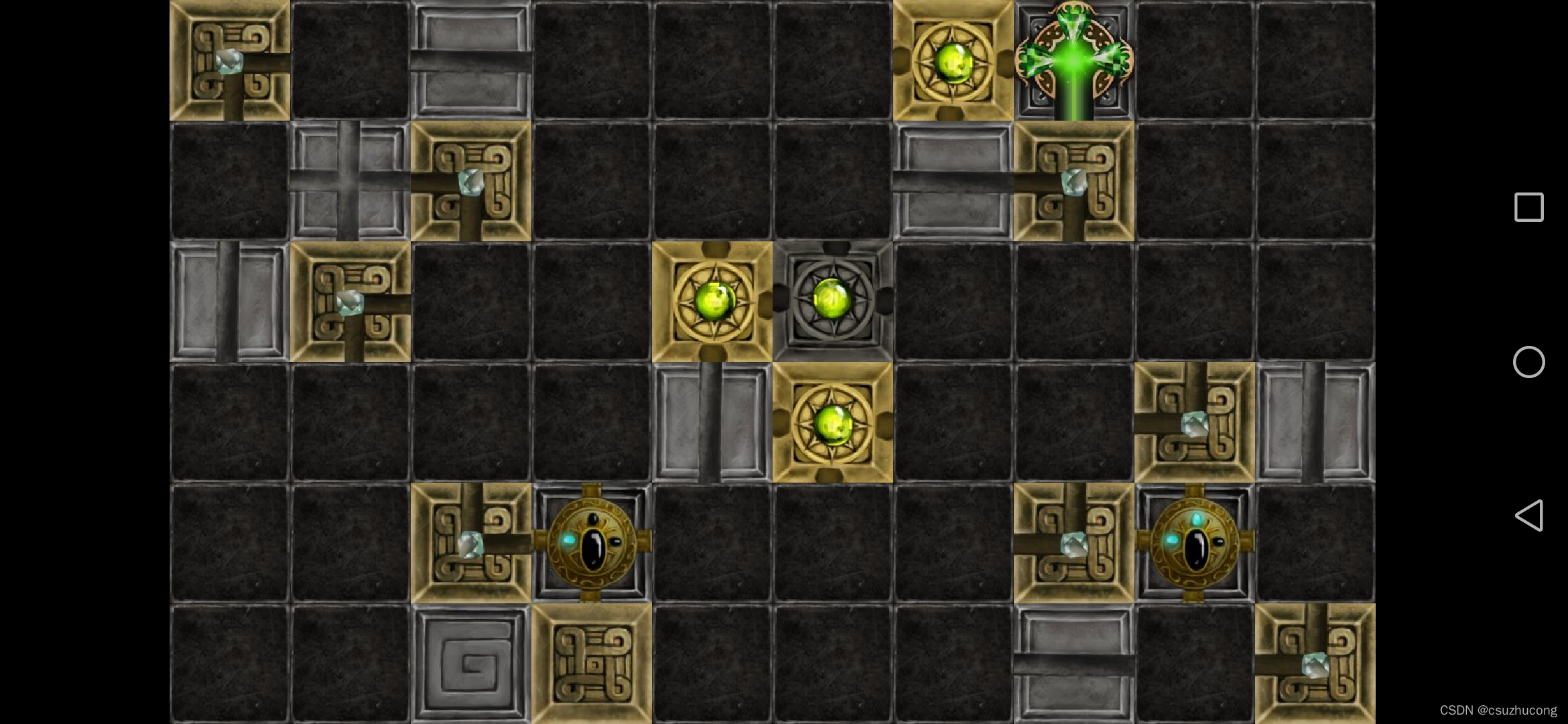
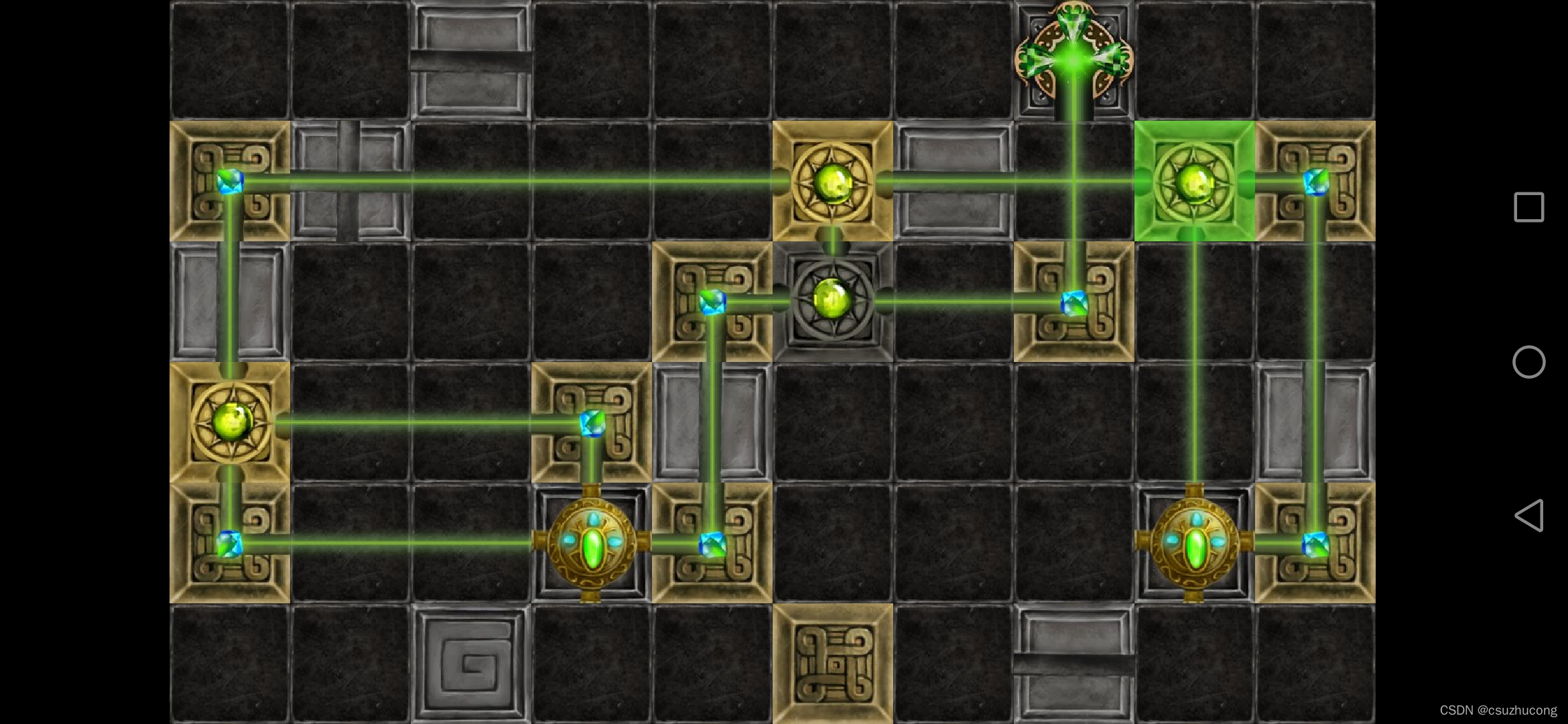
2-5

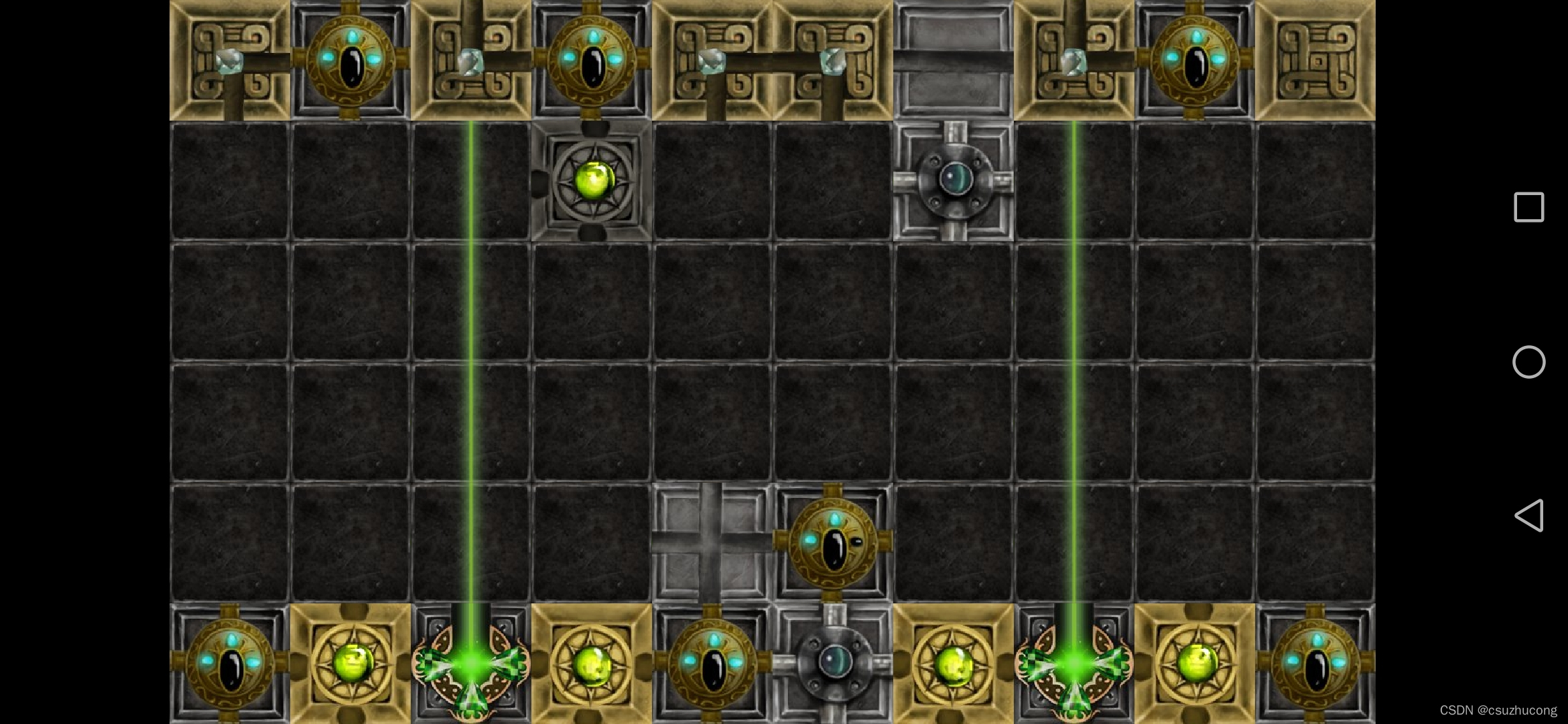
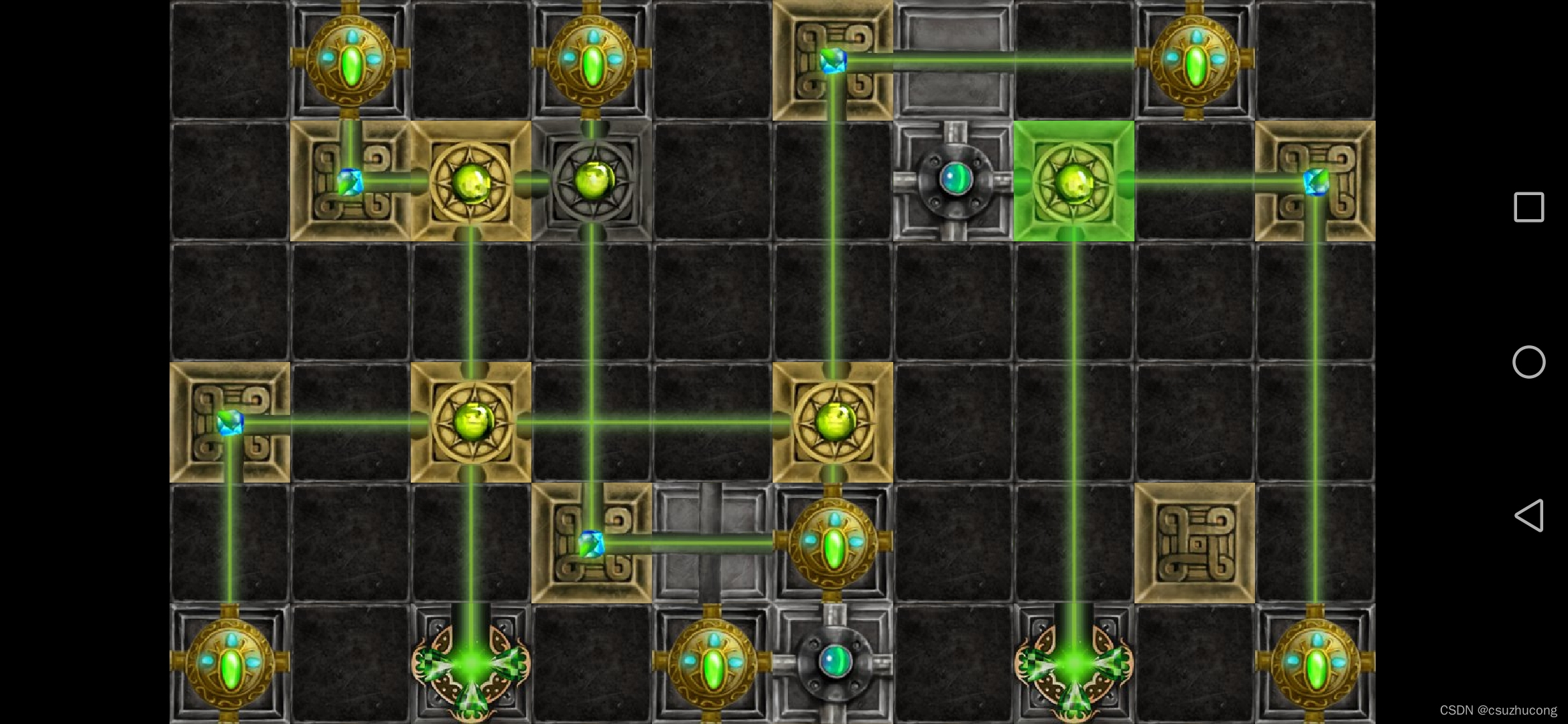
2-6

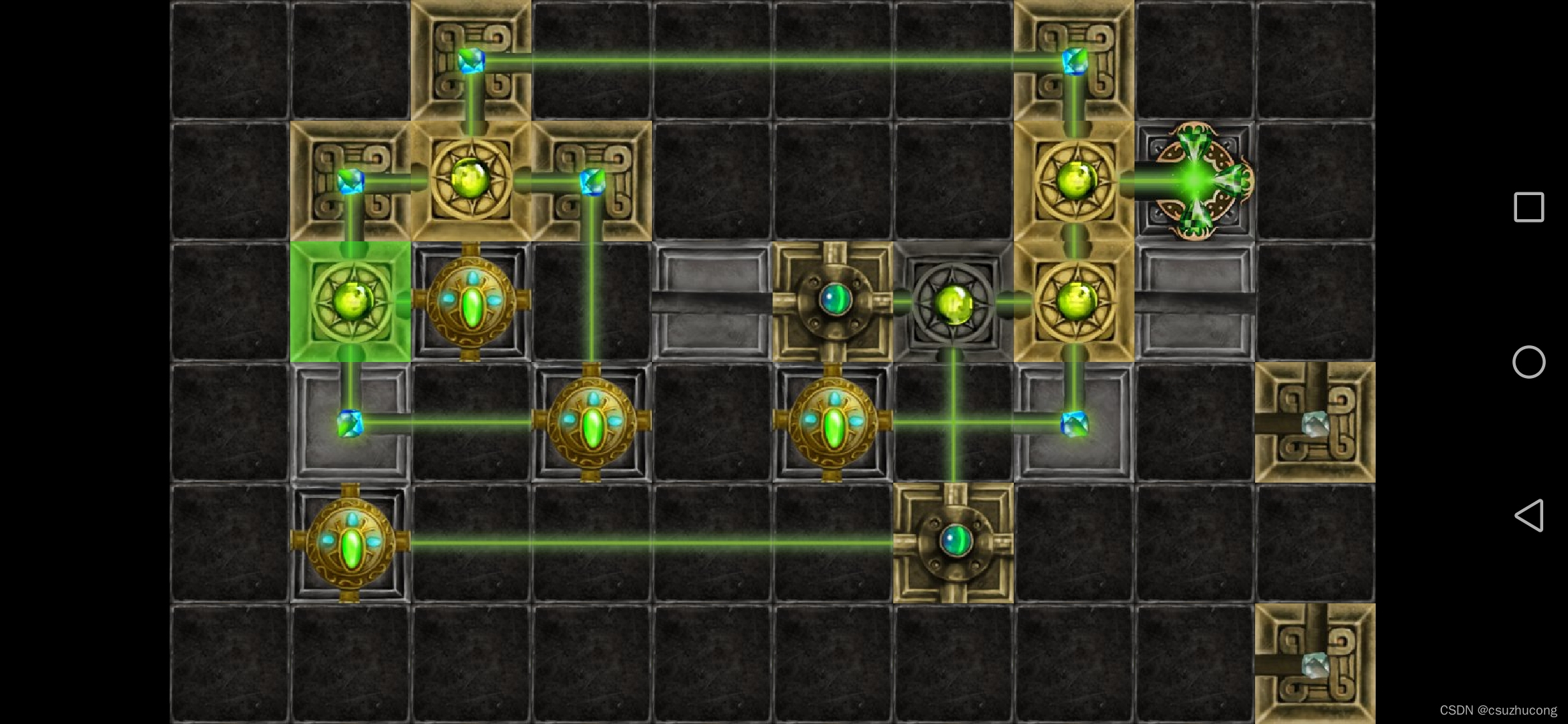
光束总数理论

目标所需光束数<=光束的总数<=光源数+分光器数目

其中分光器是那种射入一束光可以射出两束光的器件。

一般关卡都是目标所需光束数=光源数+分光器数目。

如2-6中的一个状态：

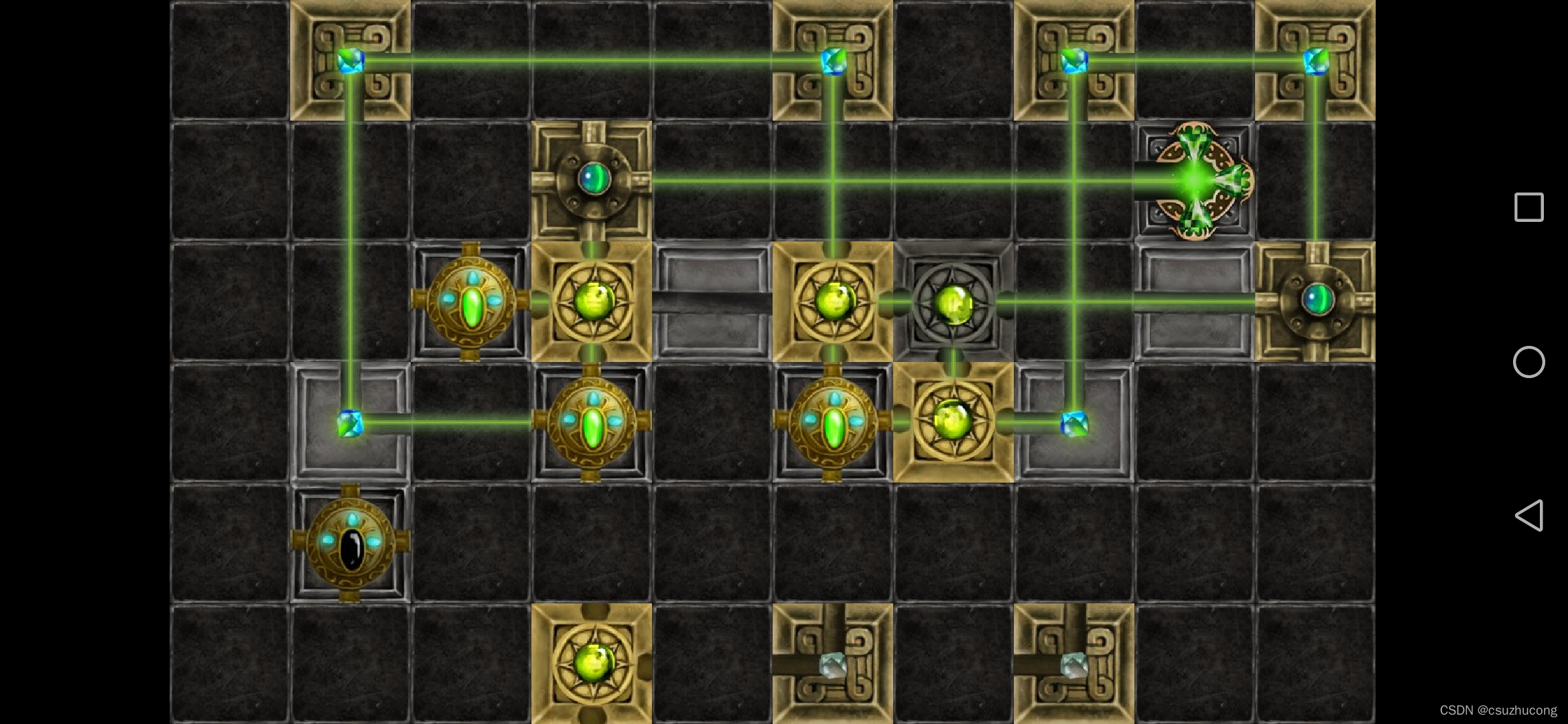
 还差一束光即可全部照亮，也还有一个分光器没有用上，没有浪费的光束。

2-7

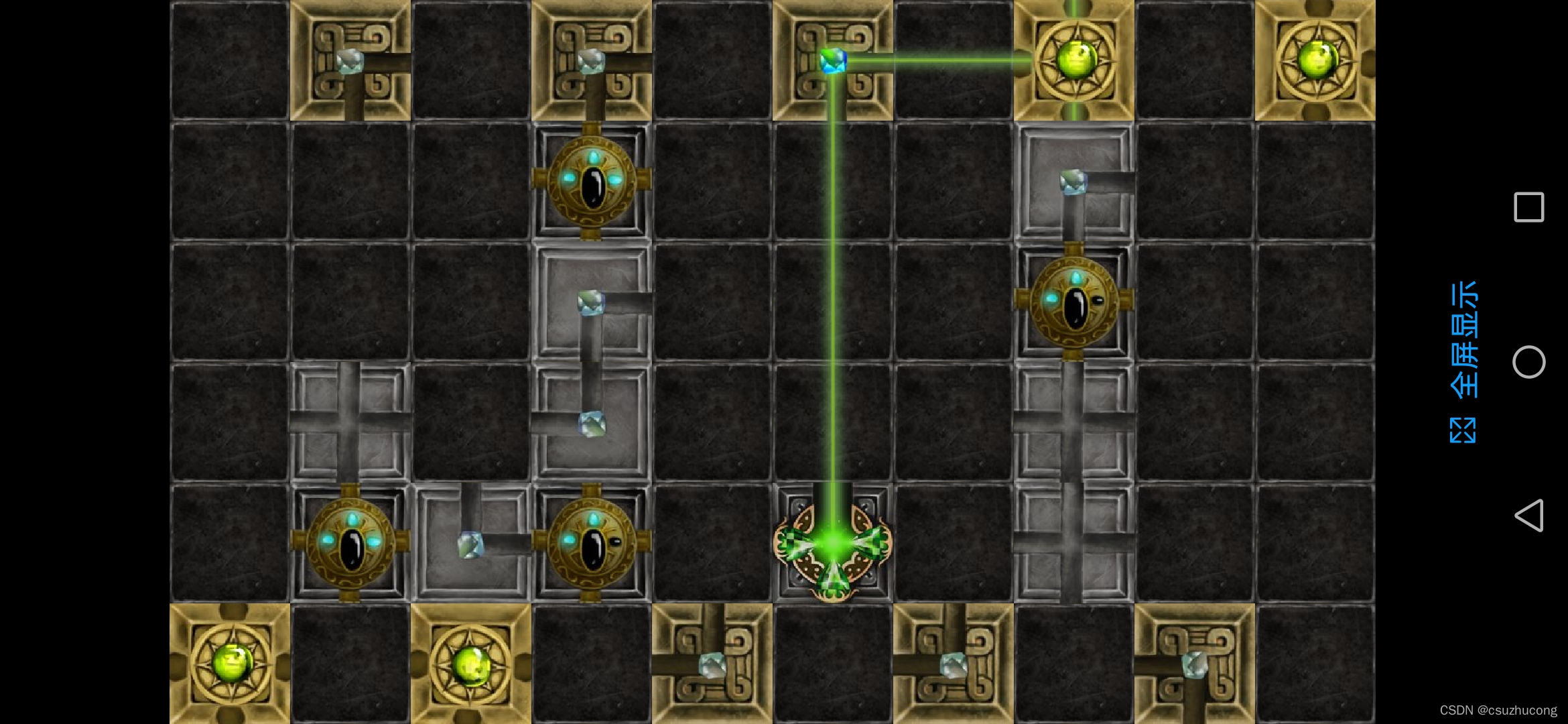
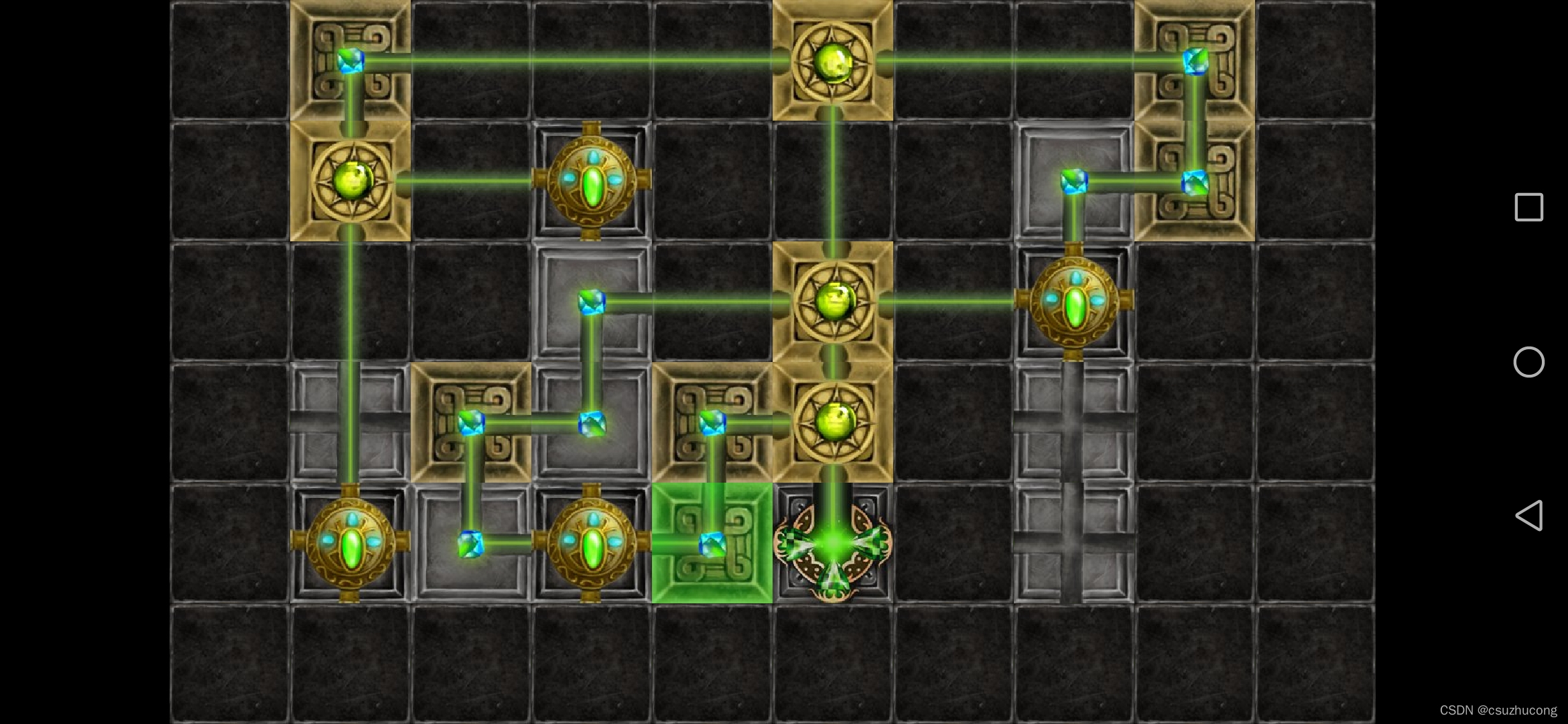
出现了三分光器，射入一束光可以射出三束光，

光束总数理论修改为 目标所需光束数<=光束的总数<=光源数+二分光器数目+三分光器数目*2

2-8

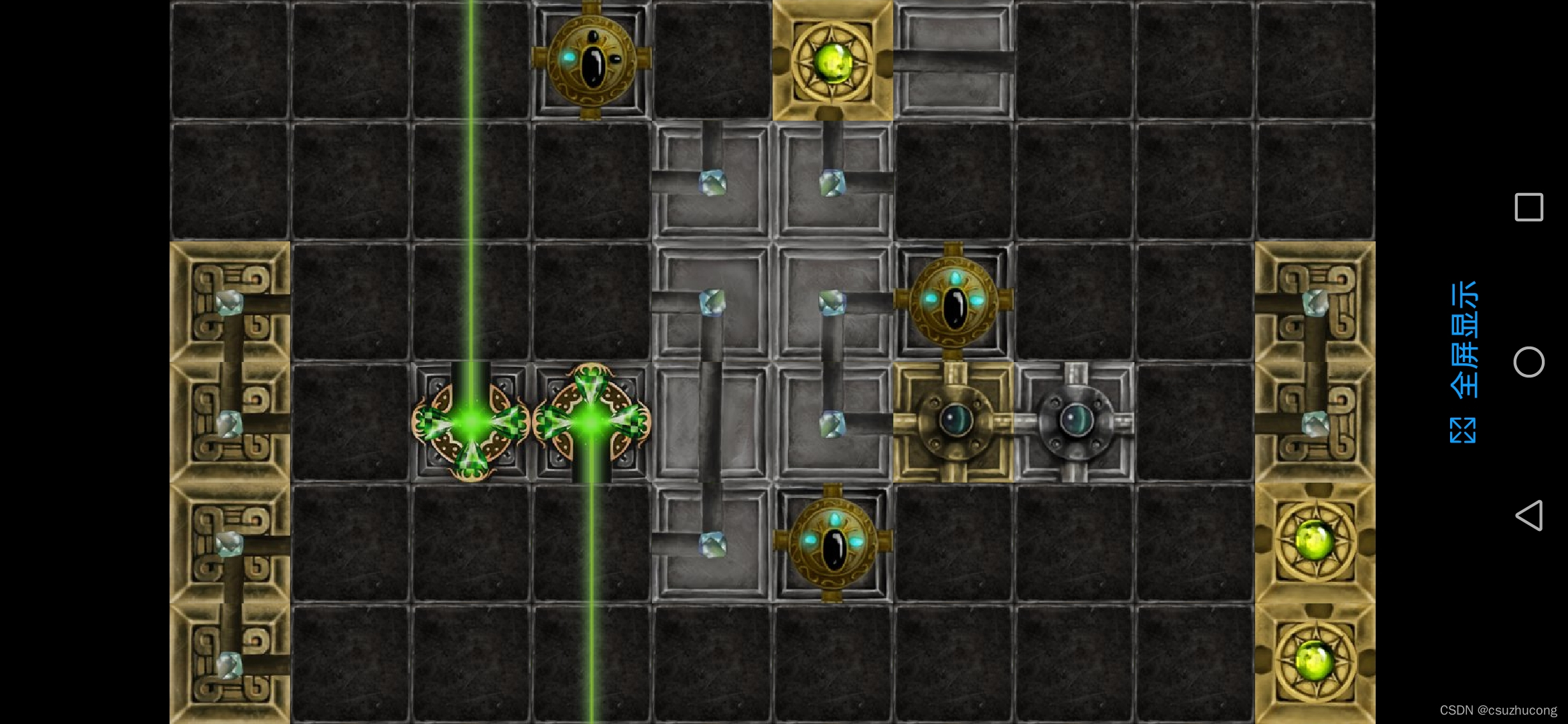
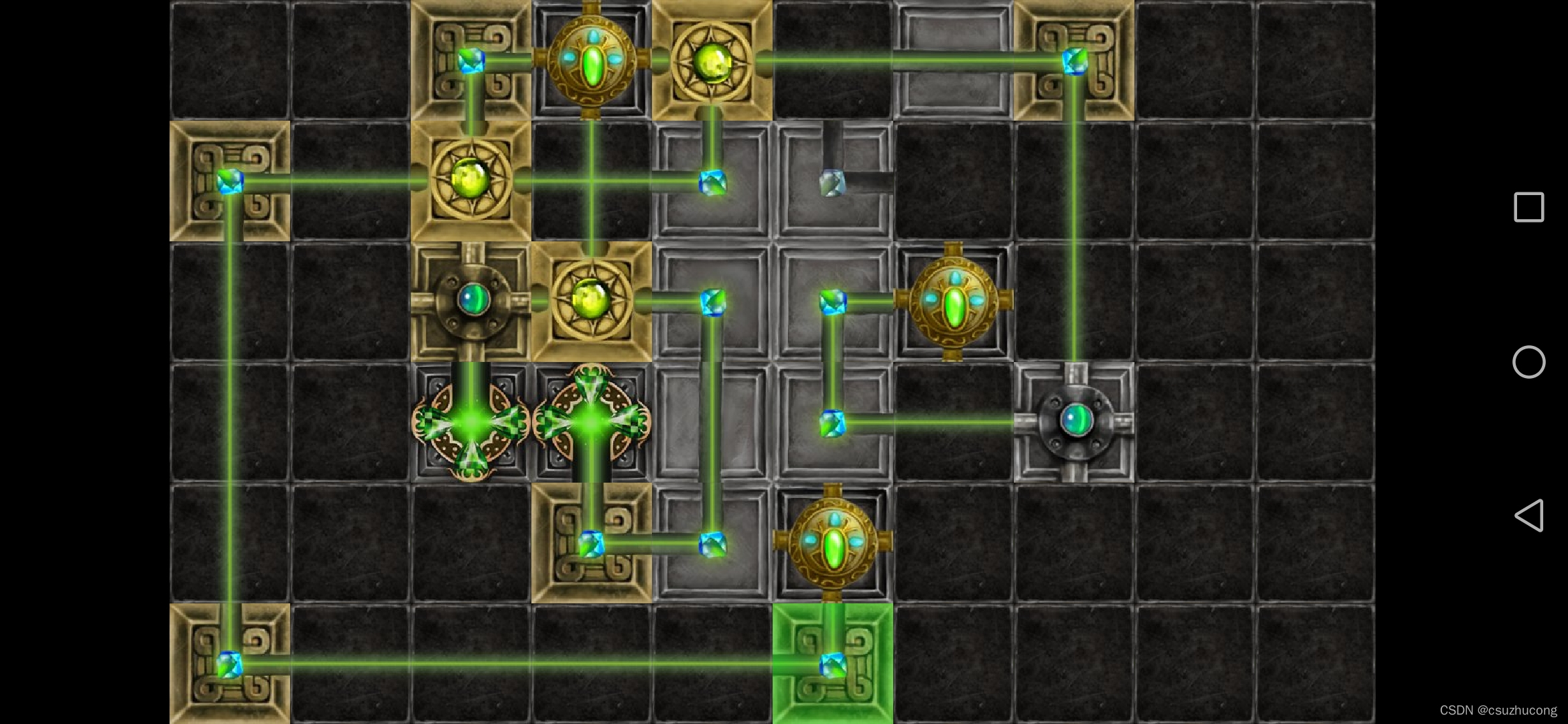
2-9

 

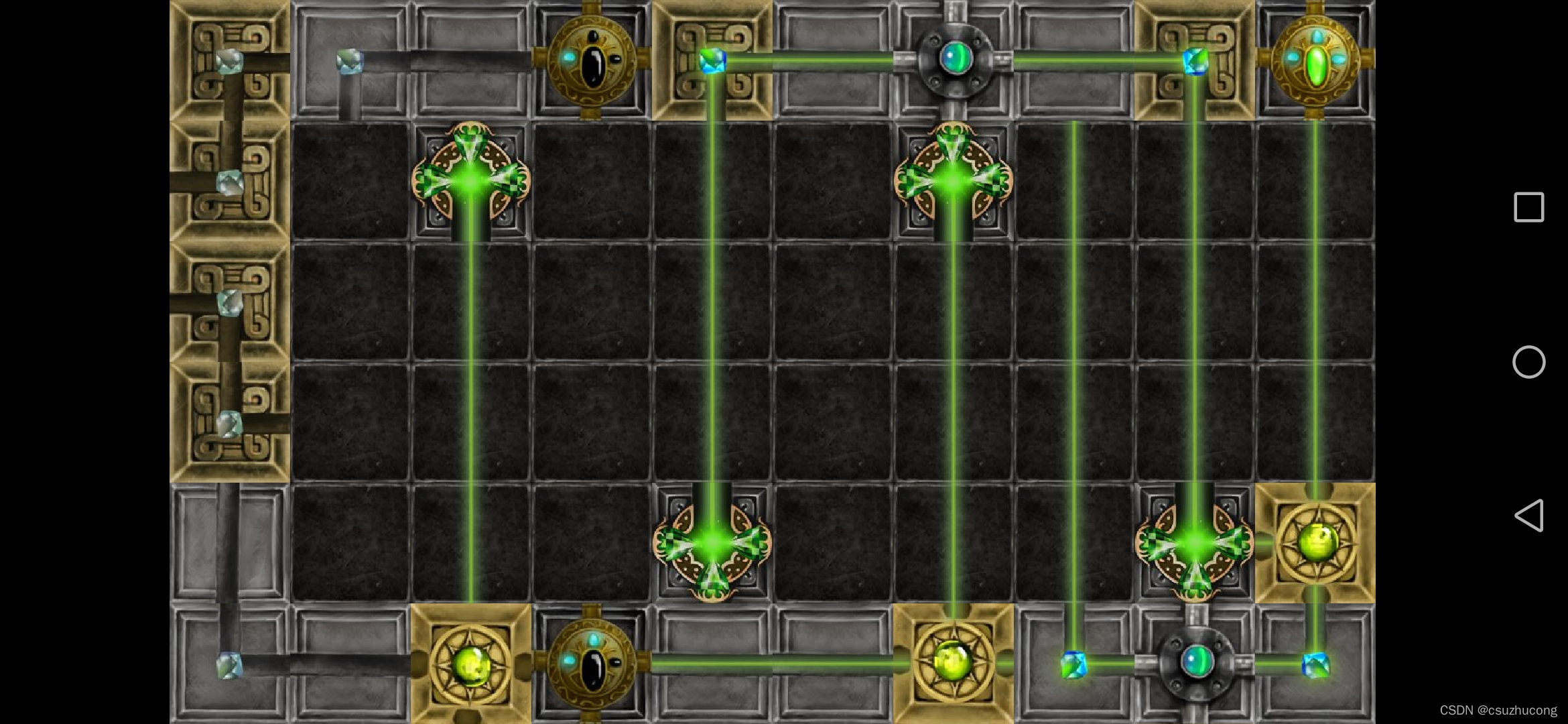
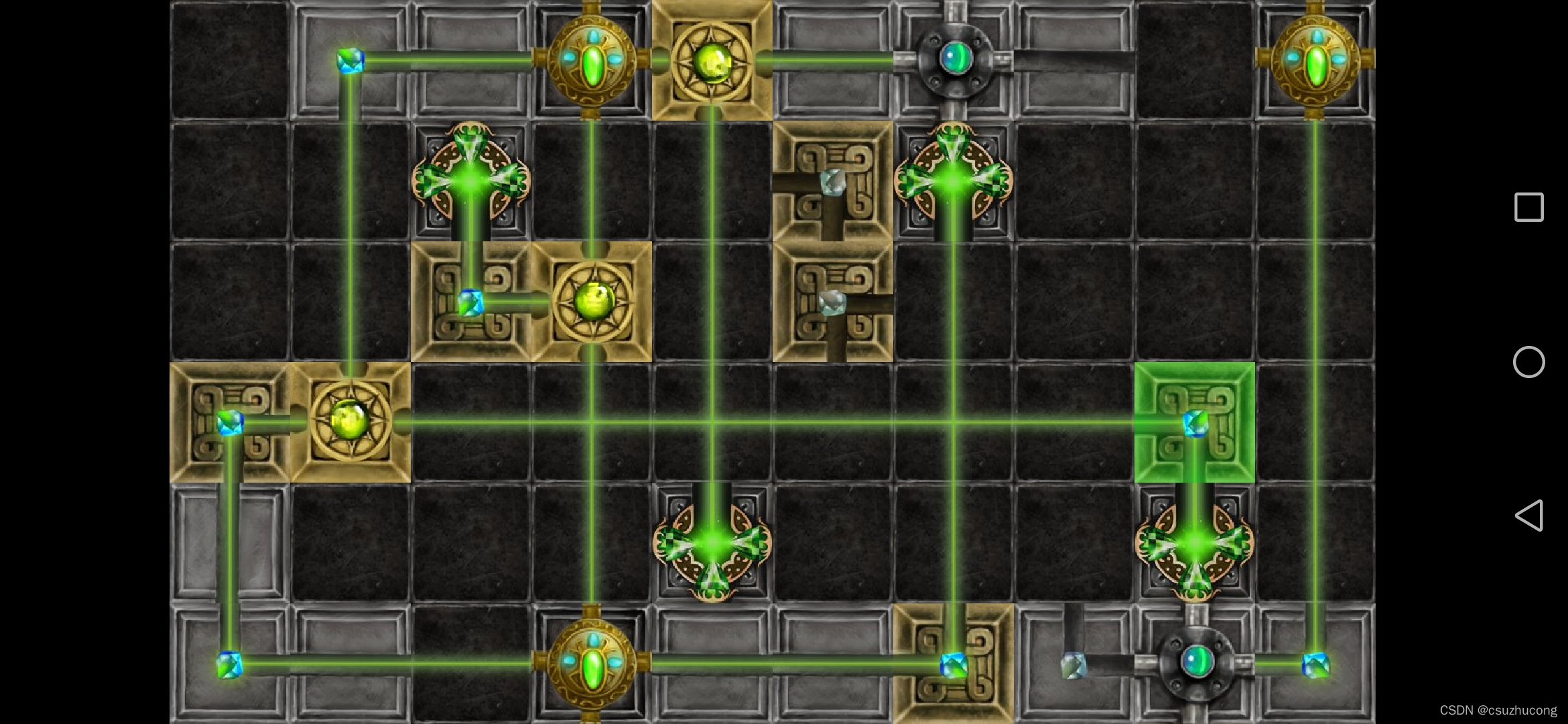
2-10

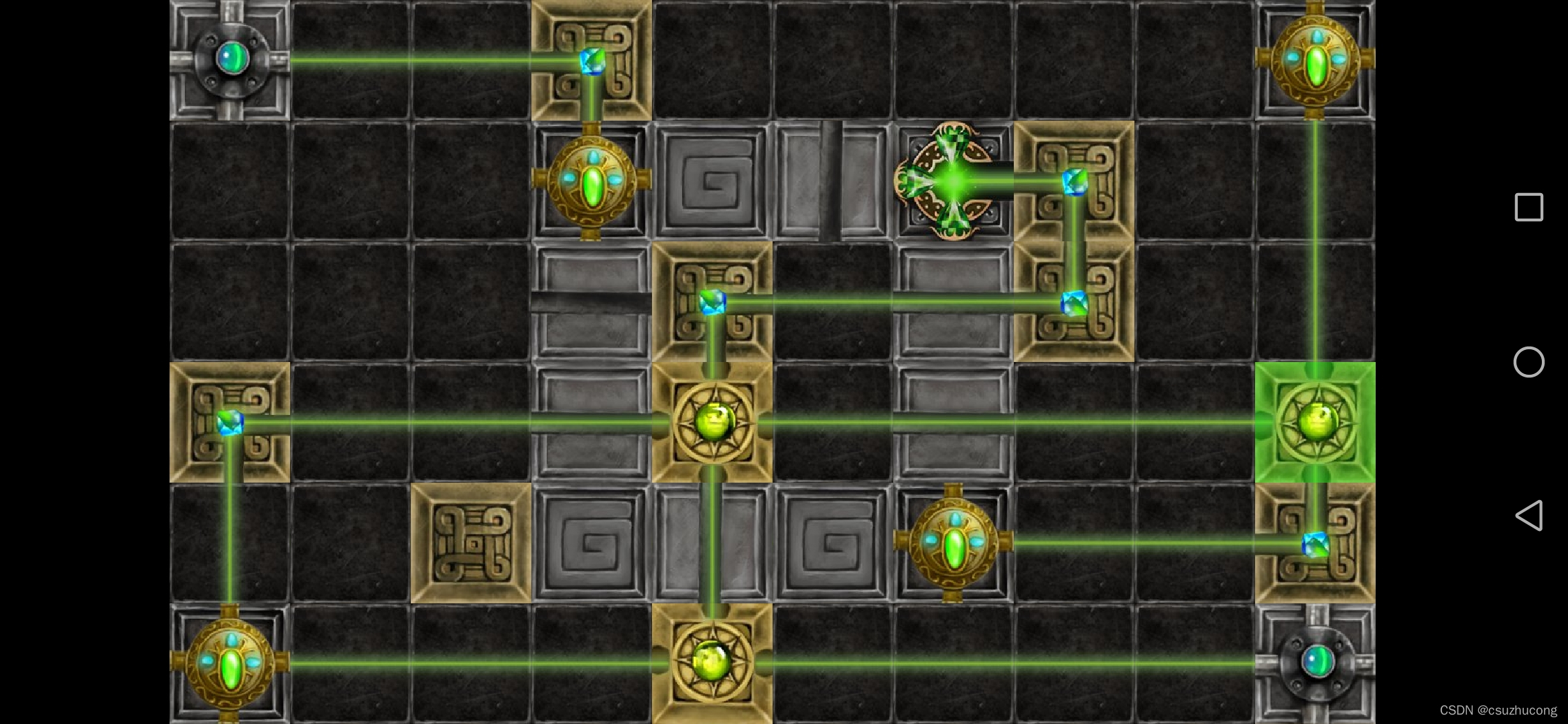
2-11

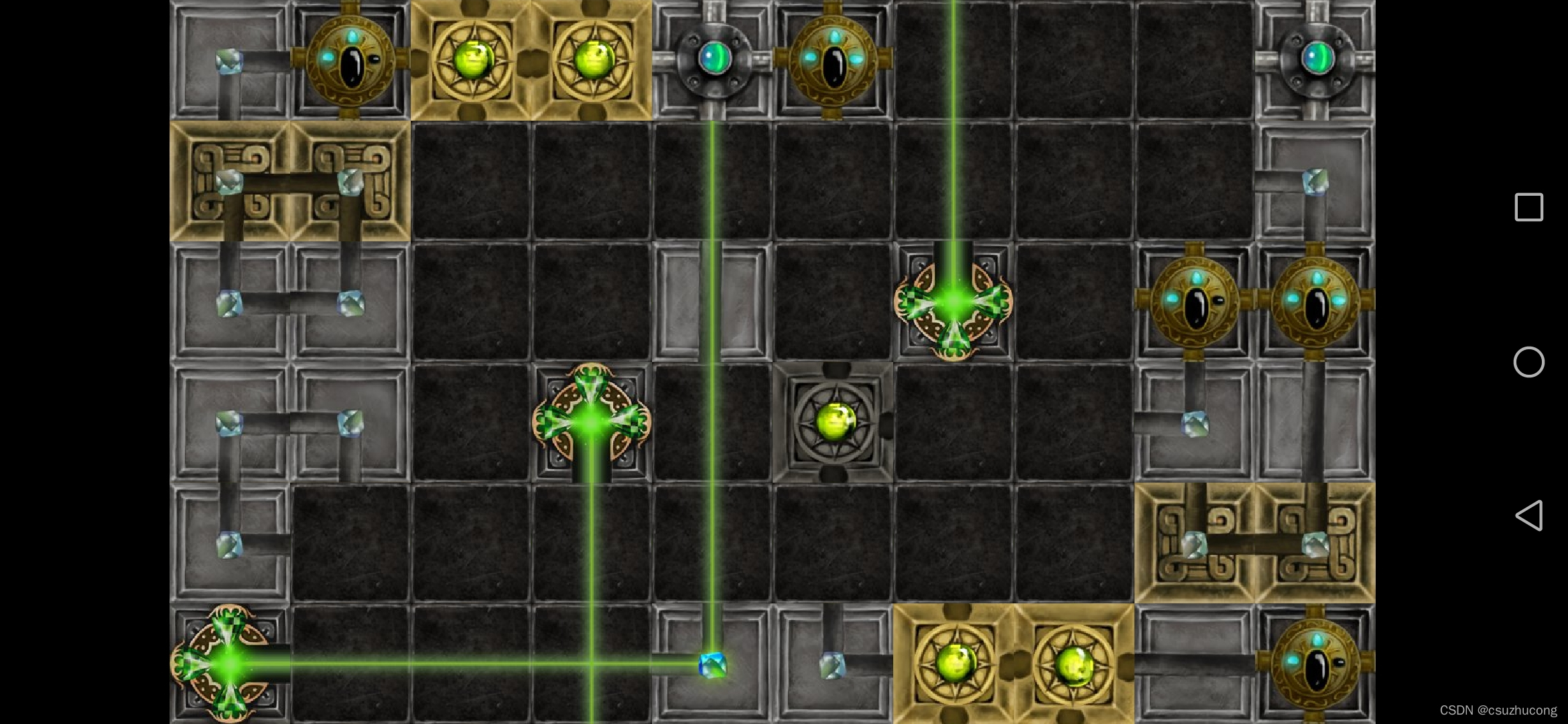
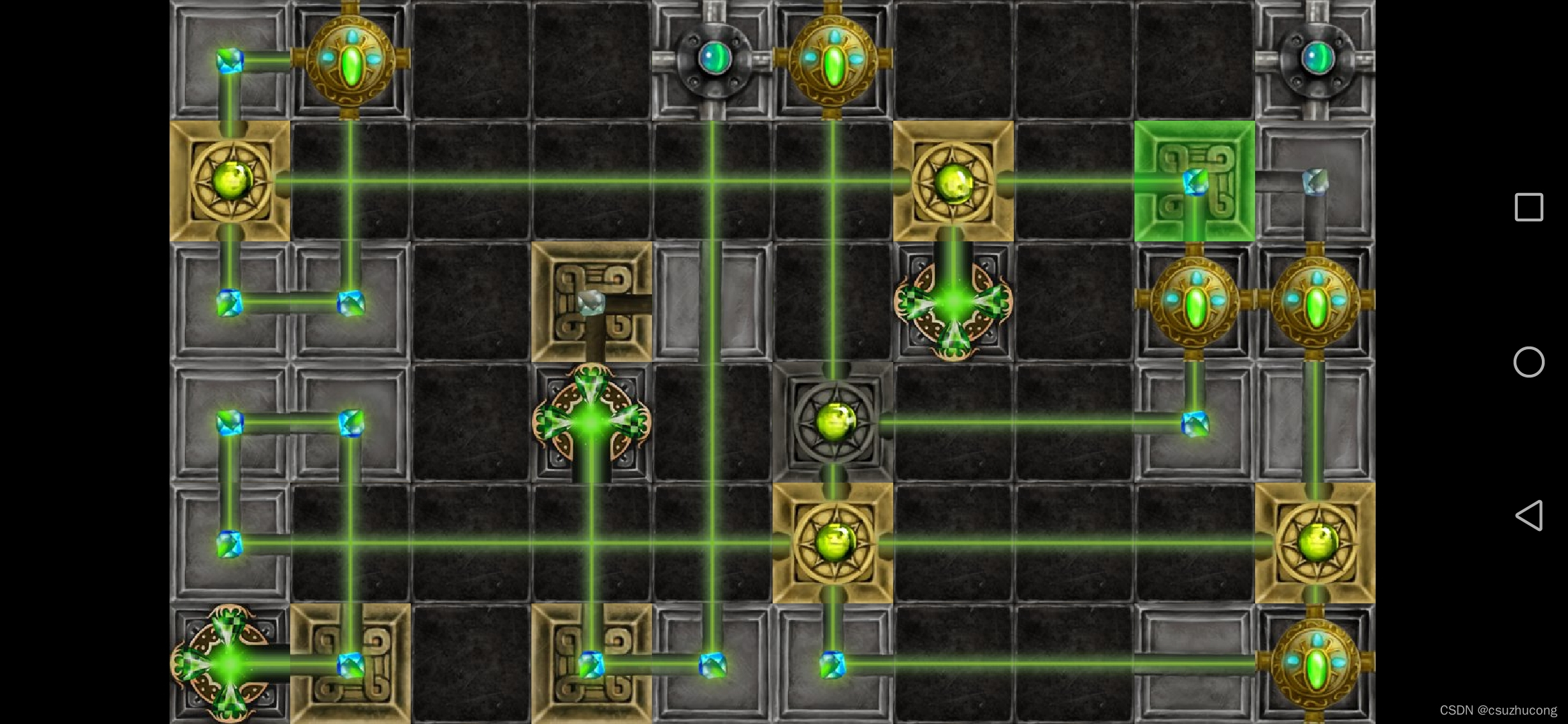
2-12

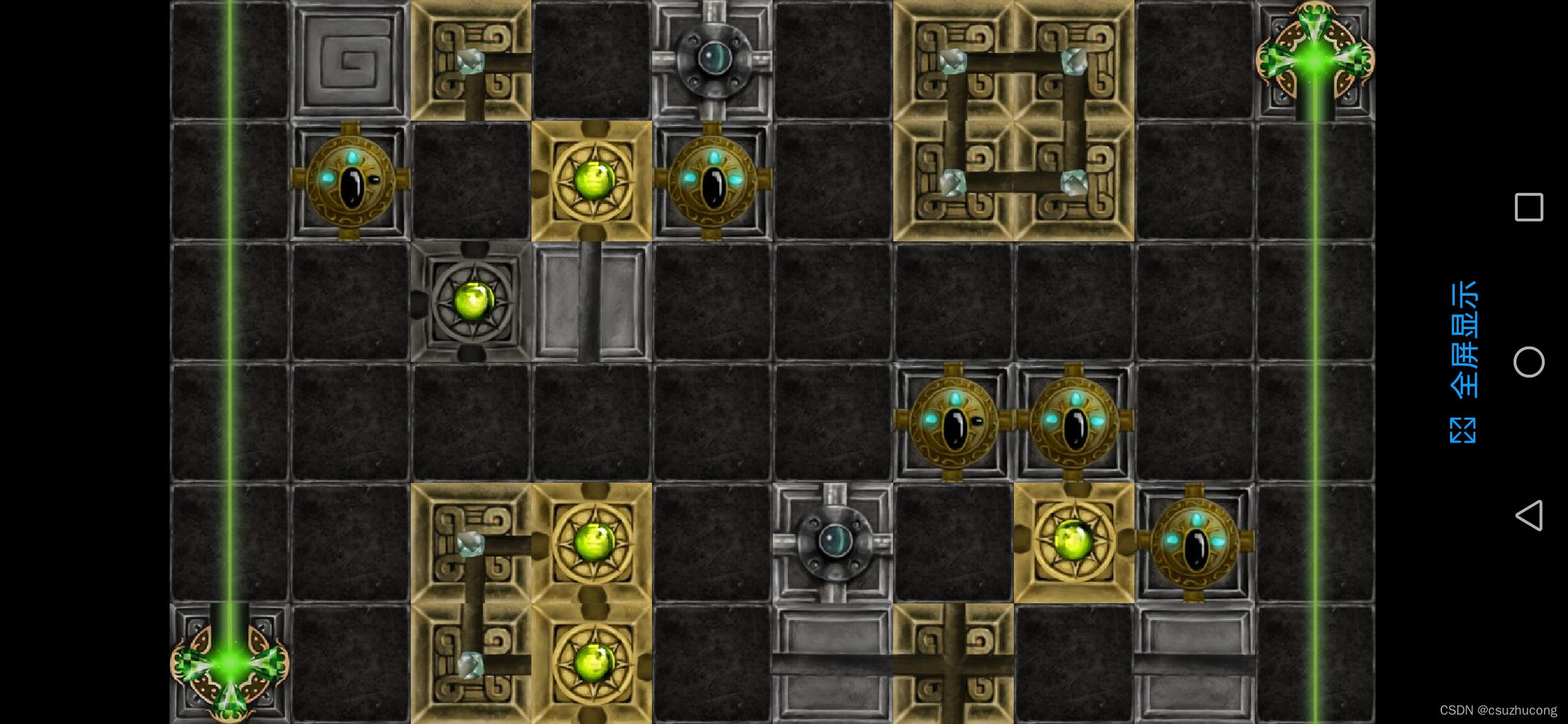
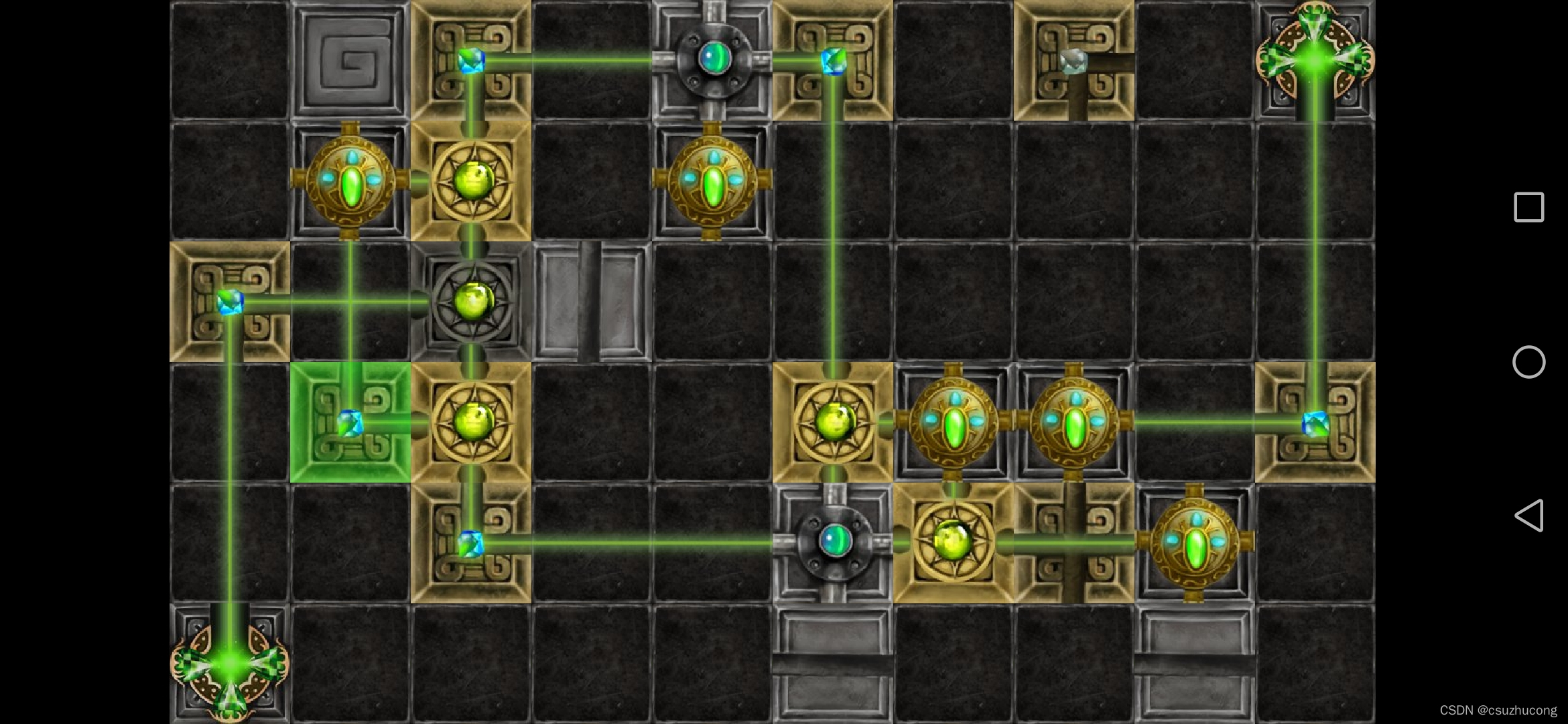
2-13

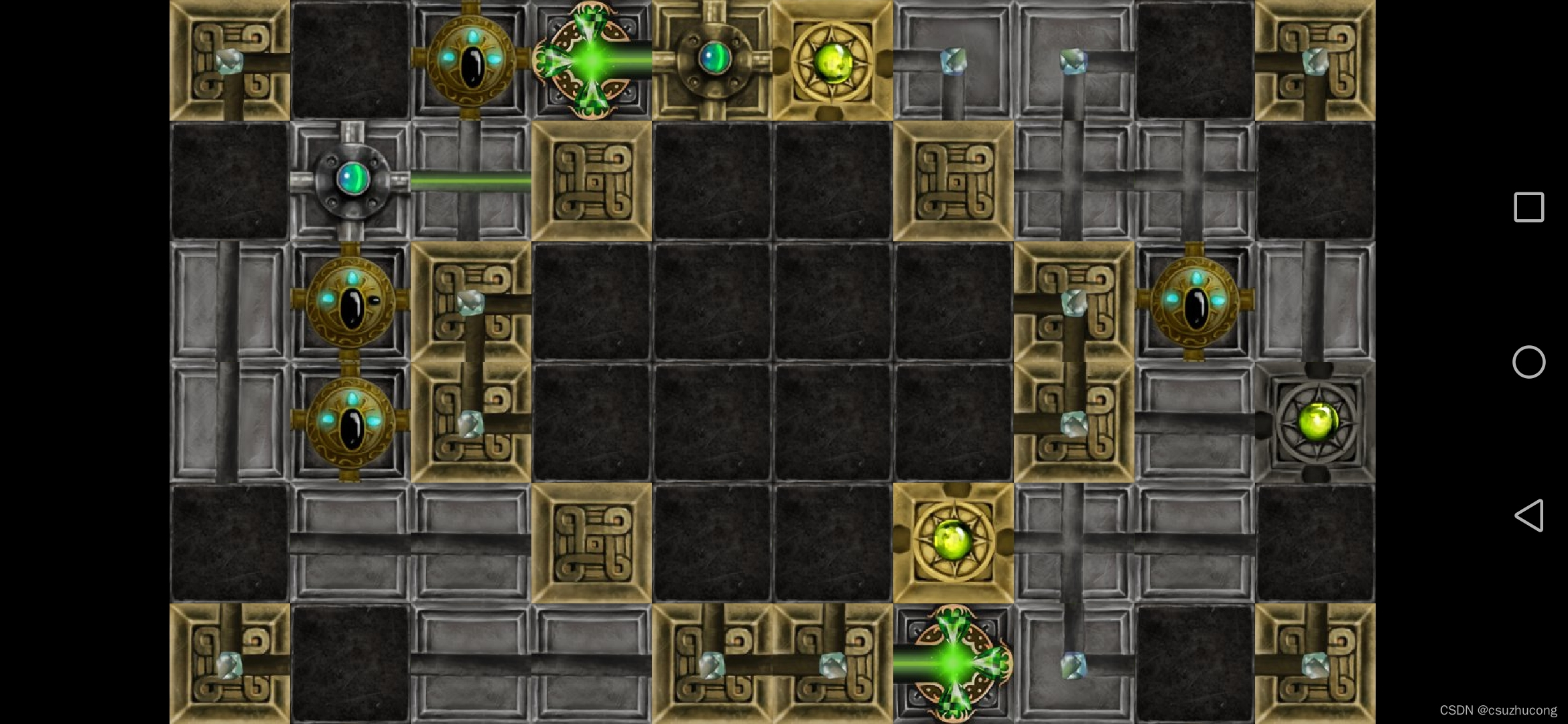
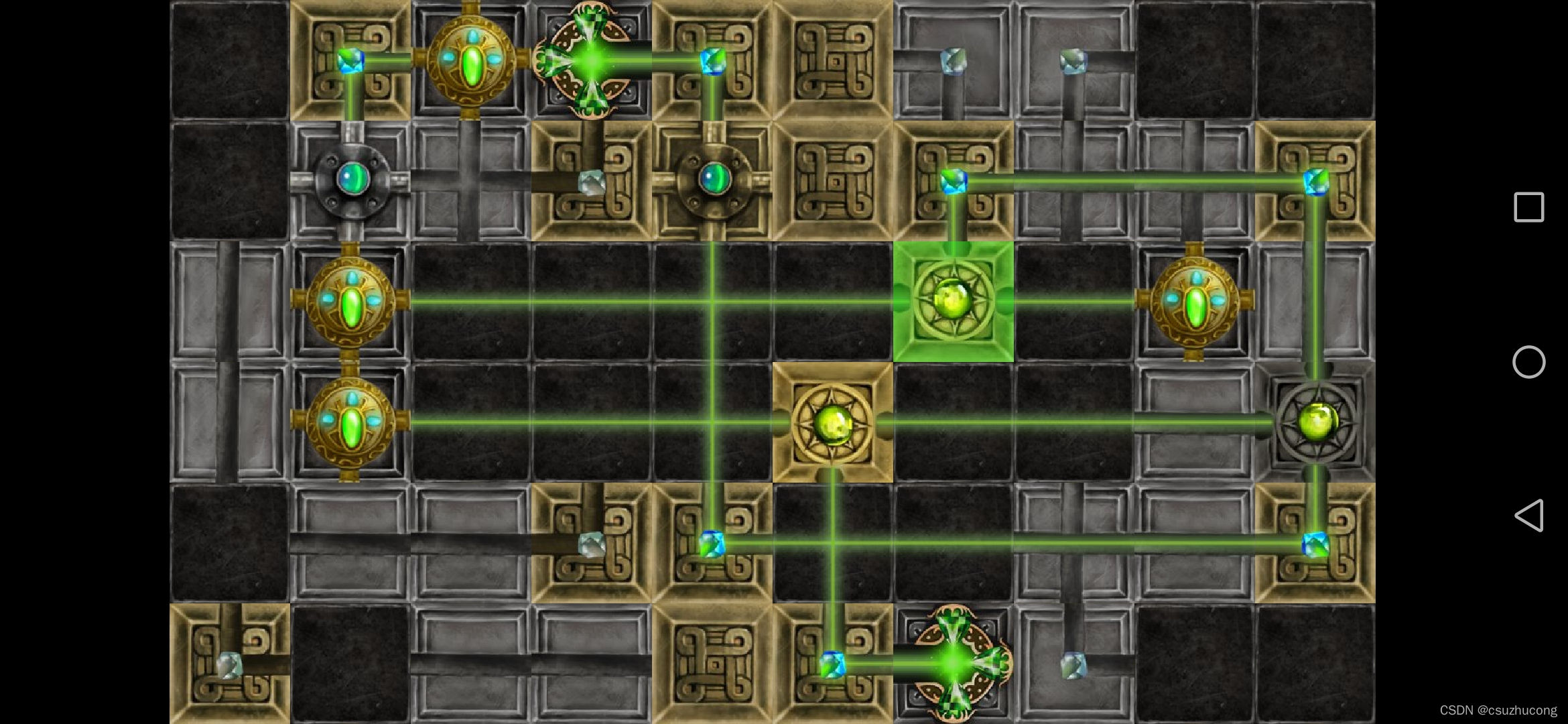
2-14

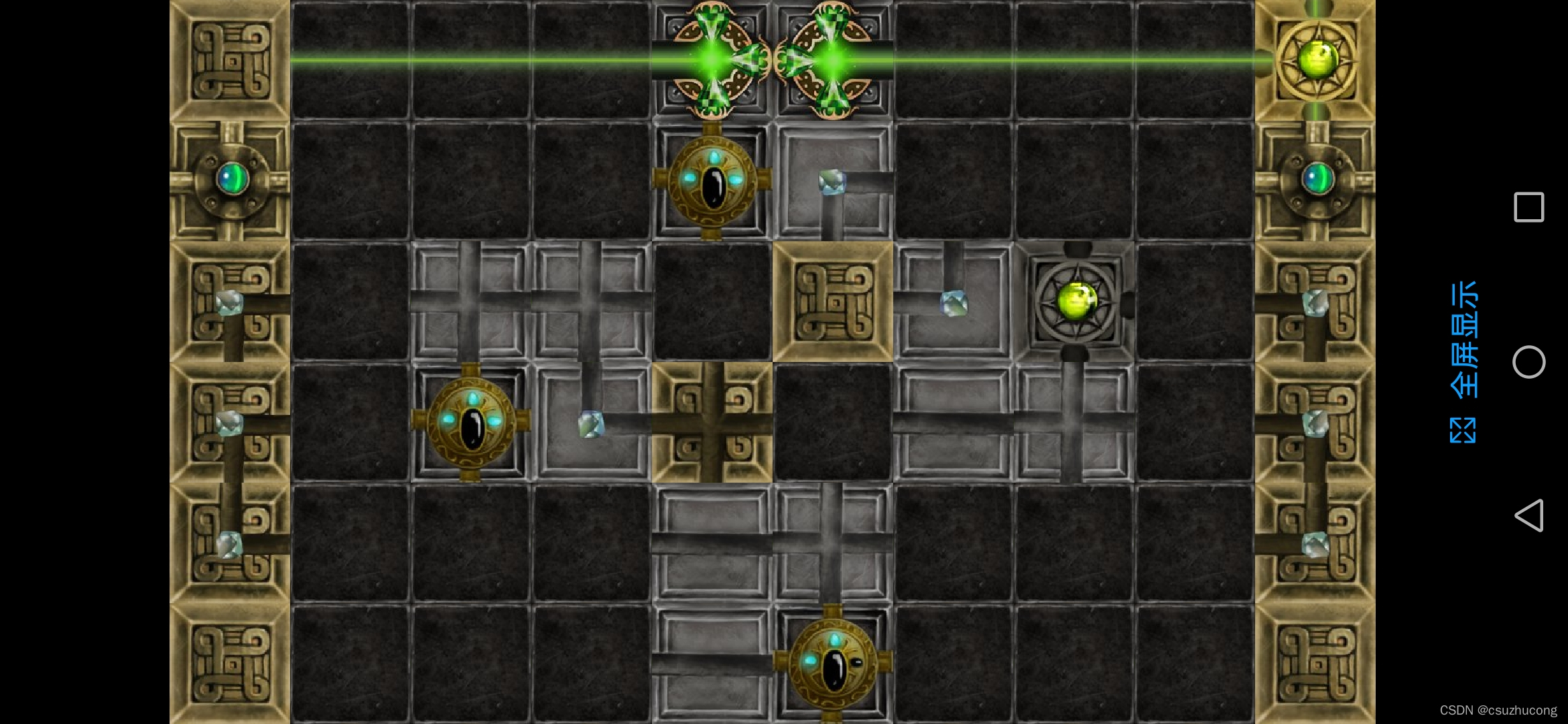
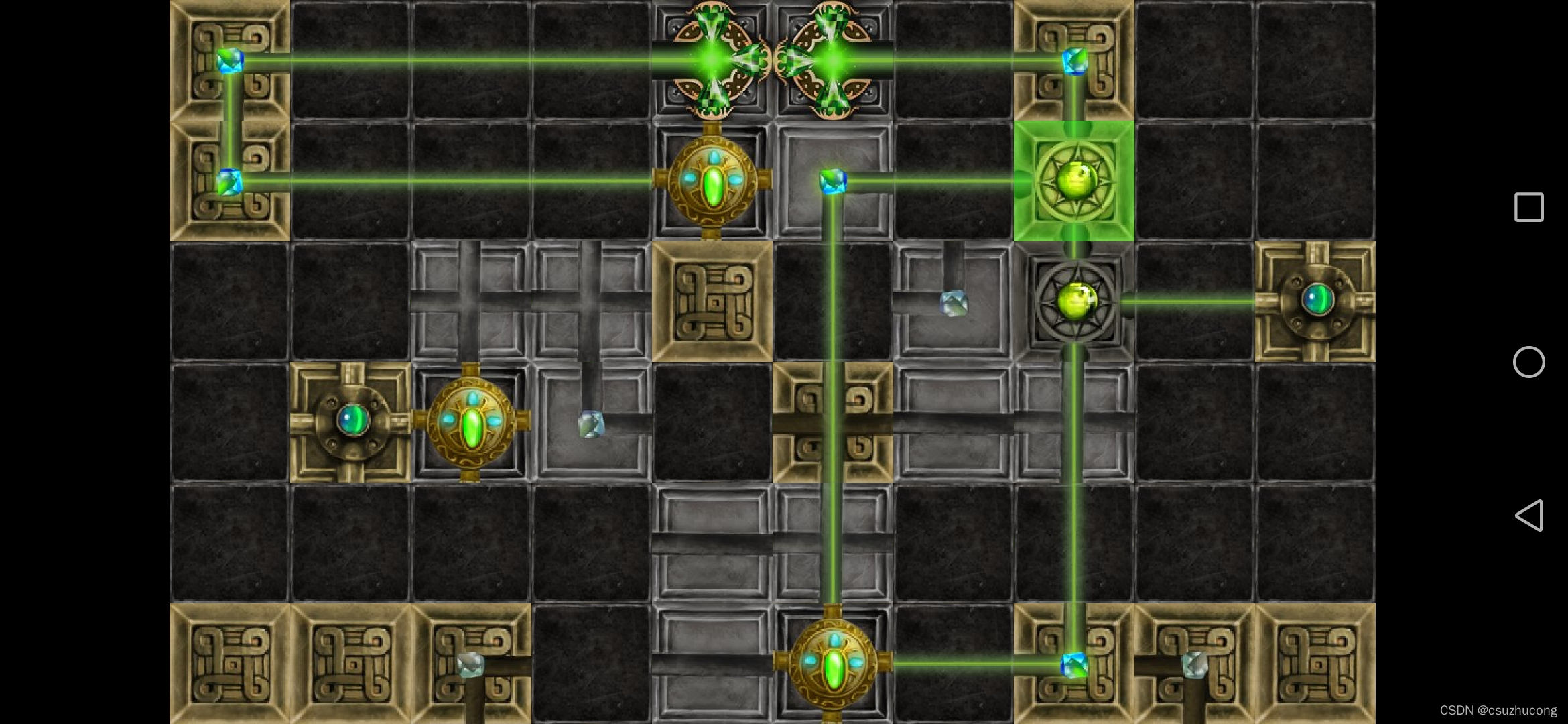
 2-15

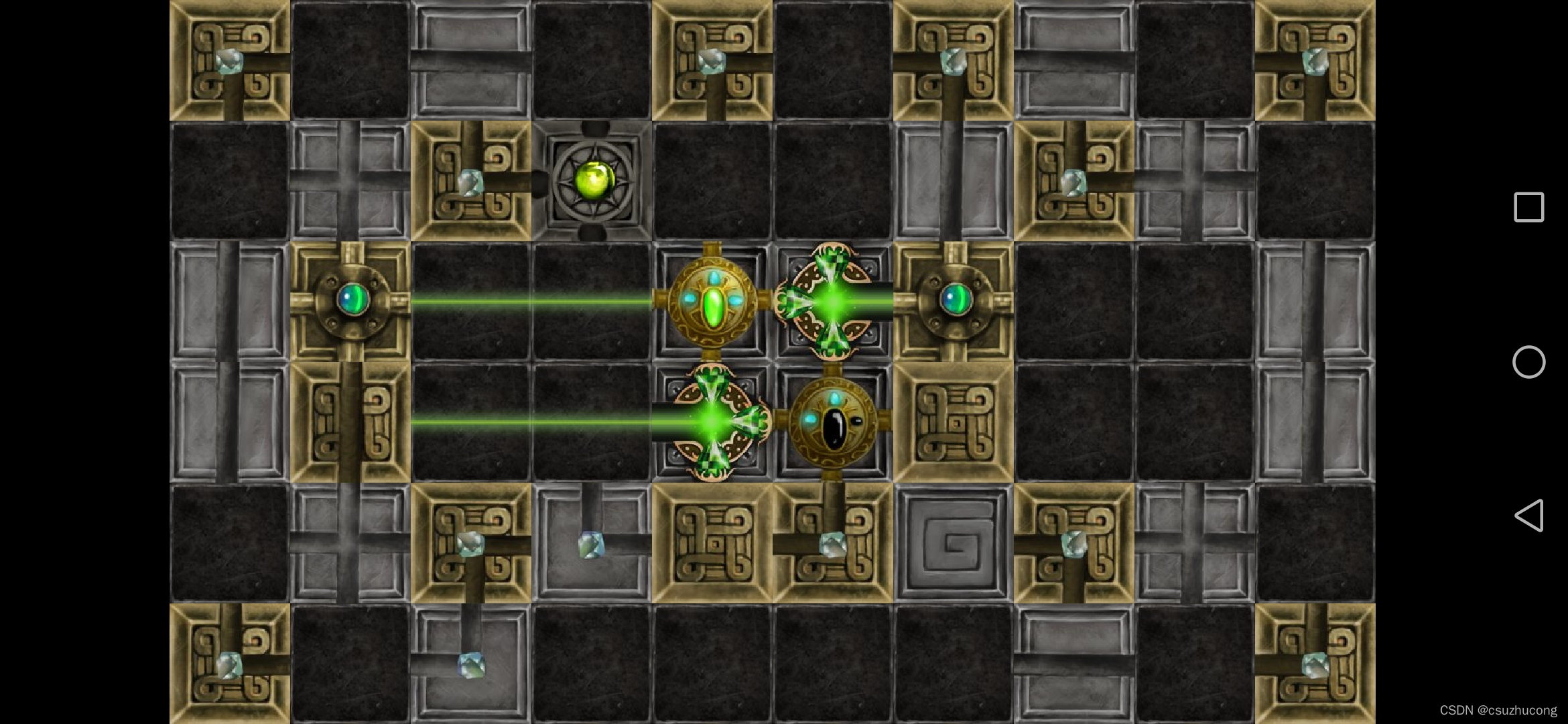
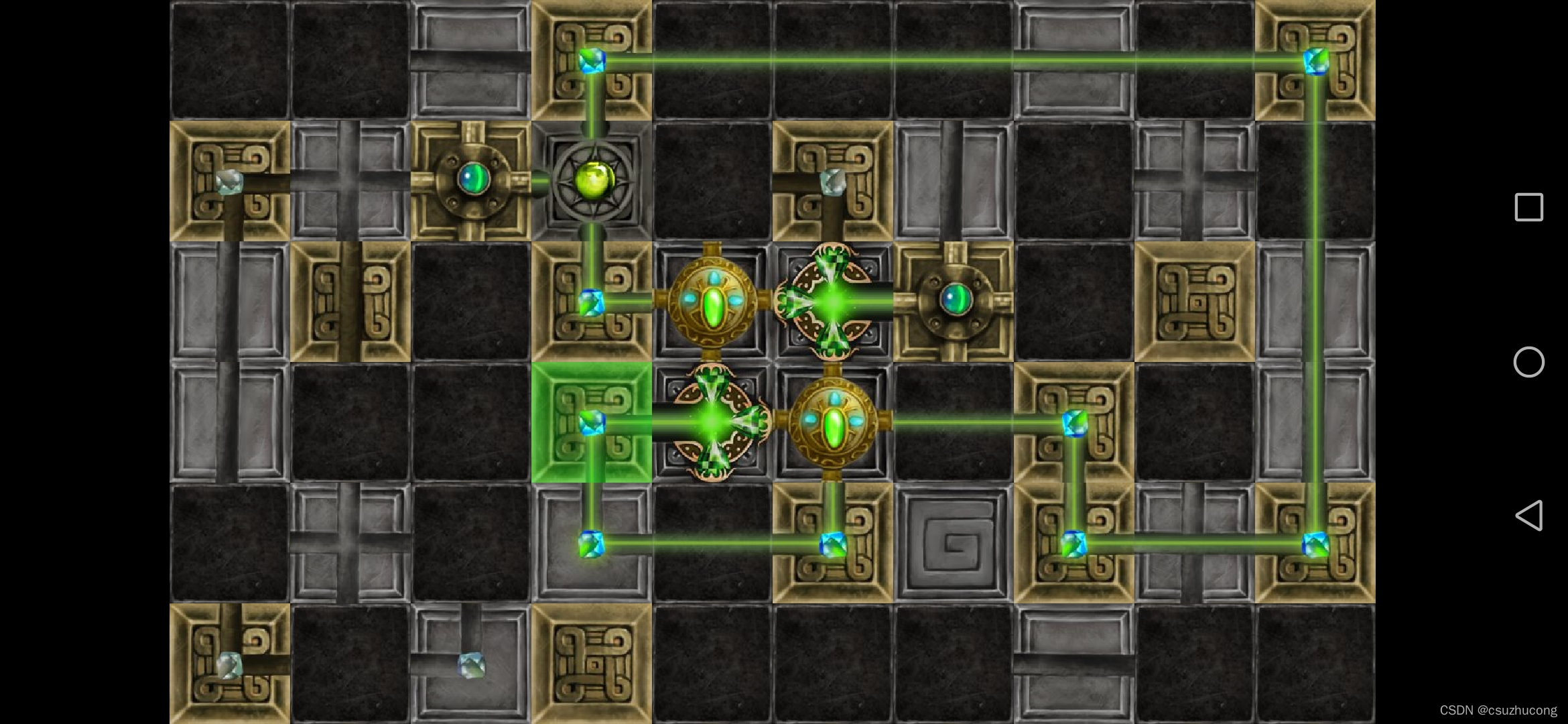
2-16

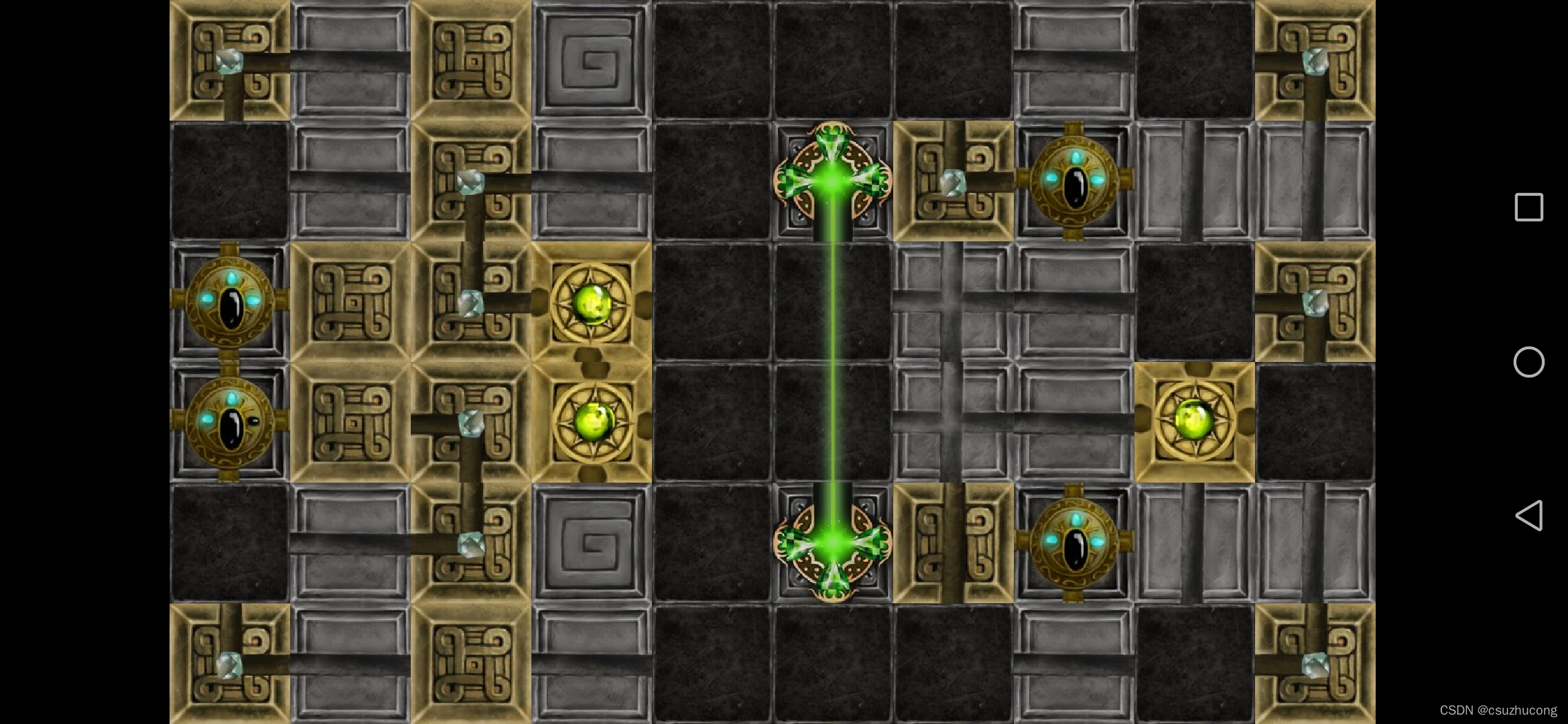
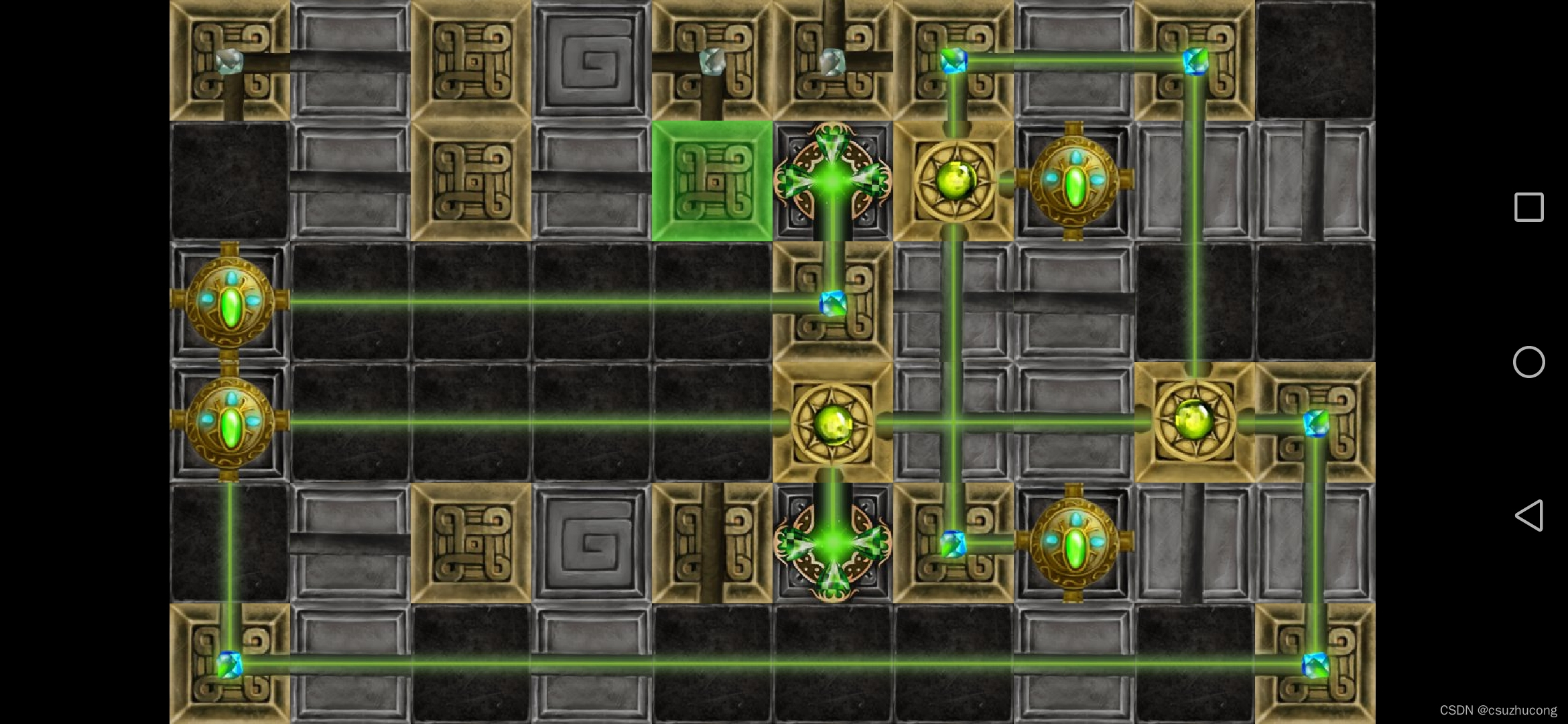
2-17

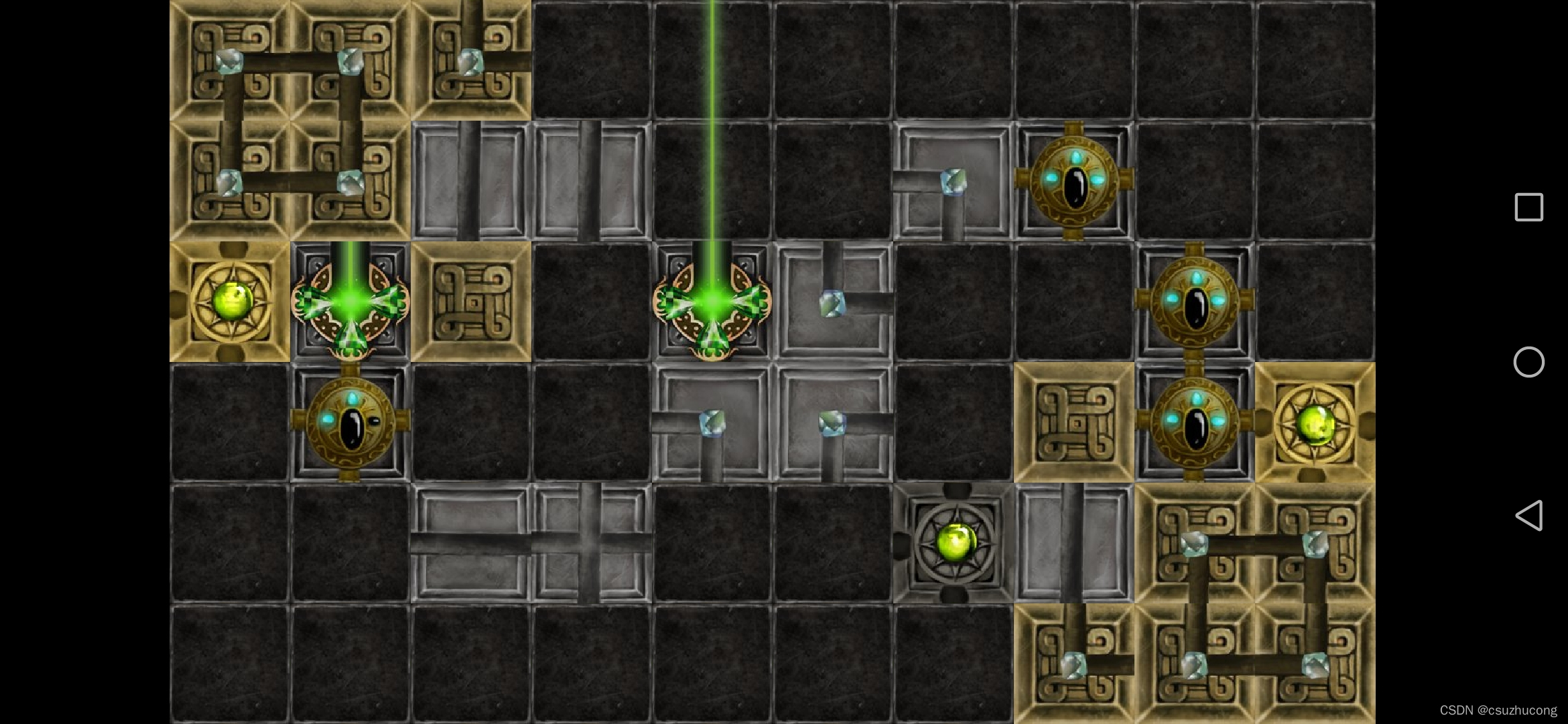
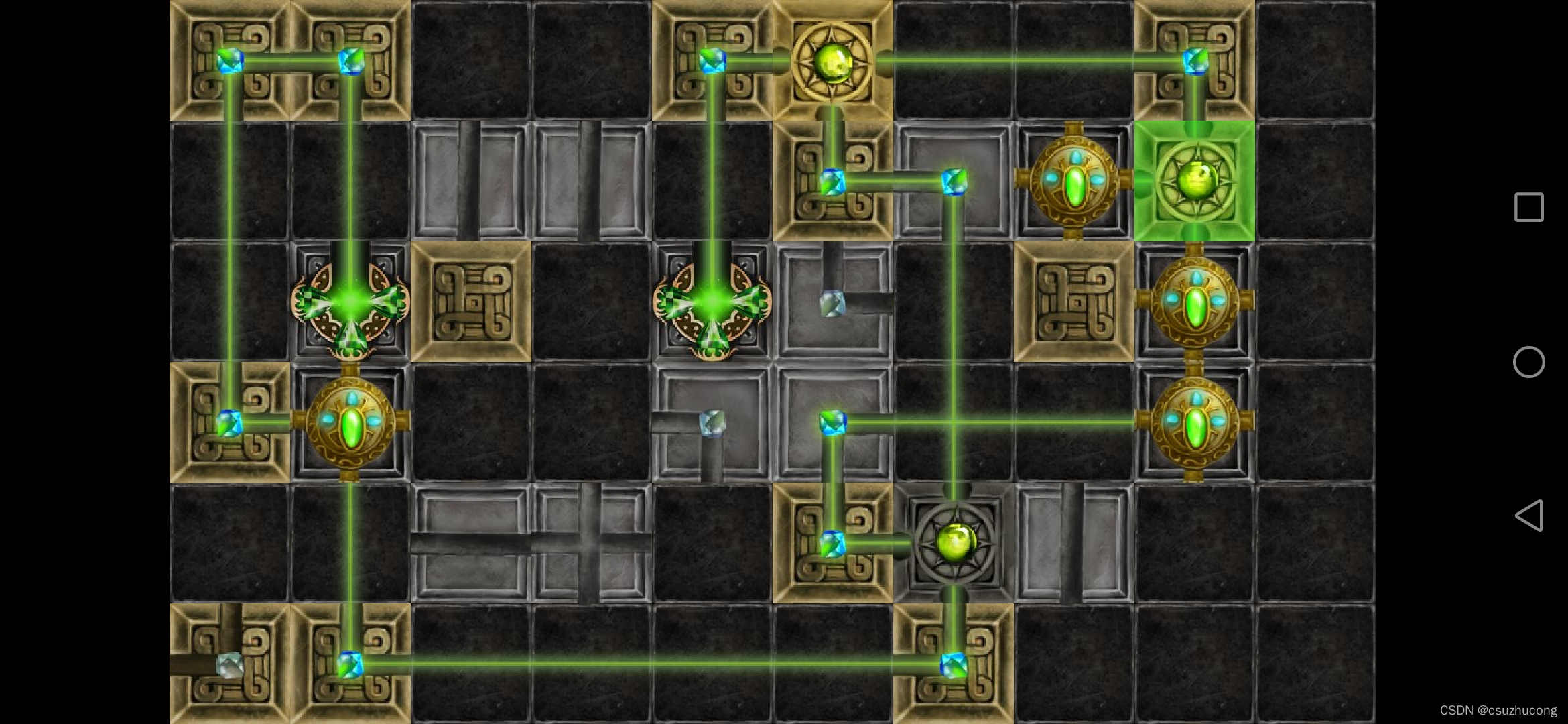
2-18

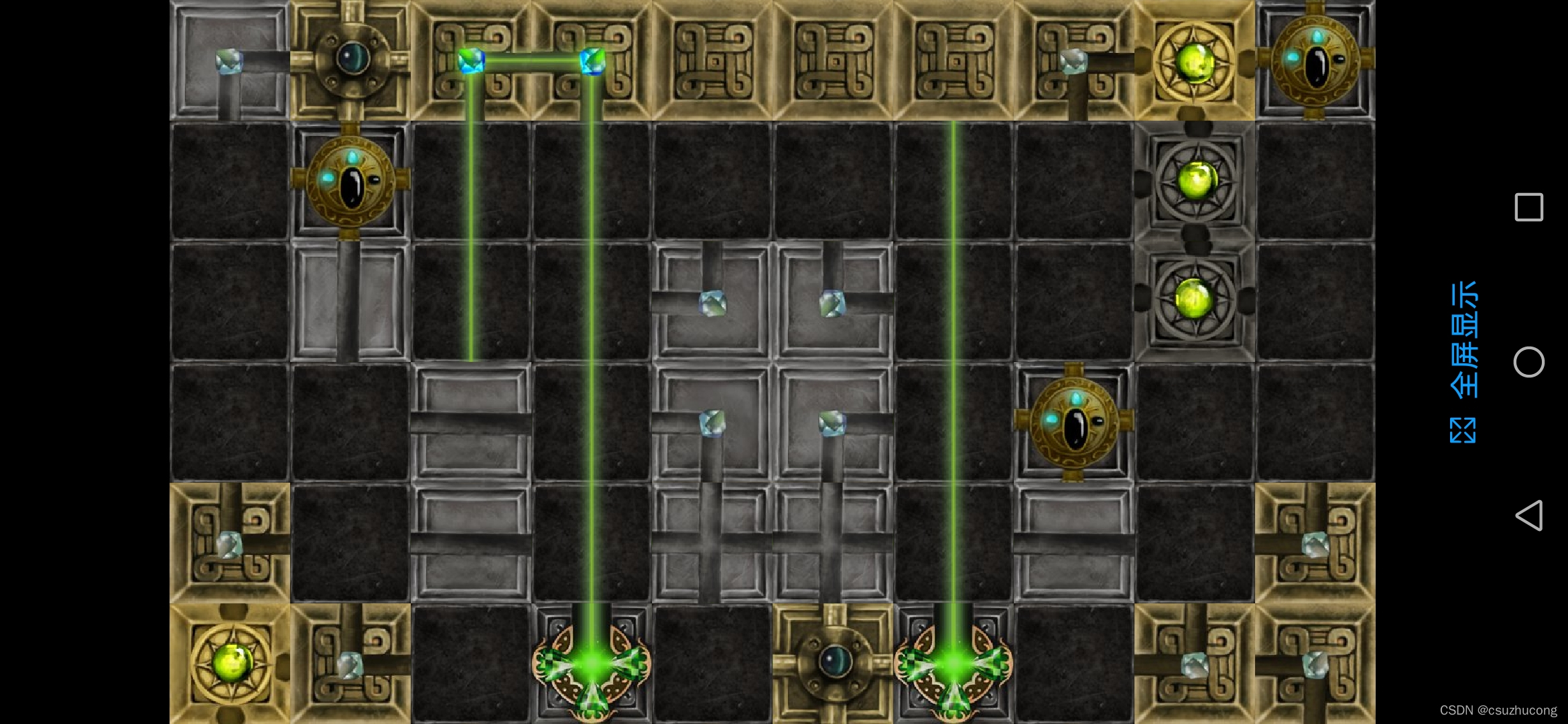
分光器的合并

2个不能移动的分光器，合并成一个大分光器，有四个口，任意一个口射入光线，射出三条光。
 

2-19

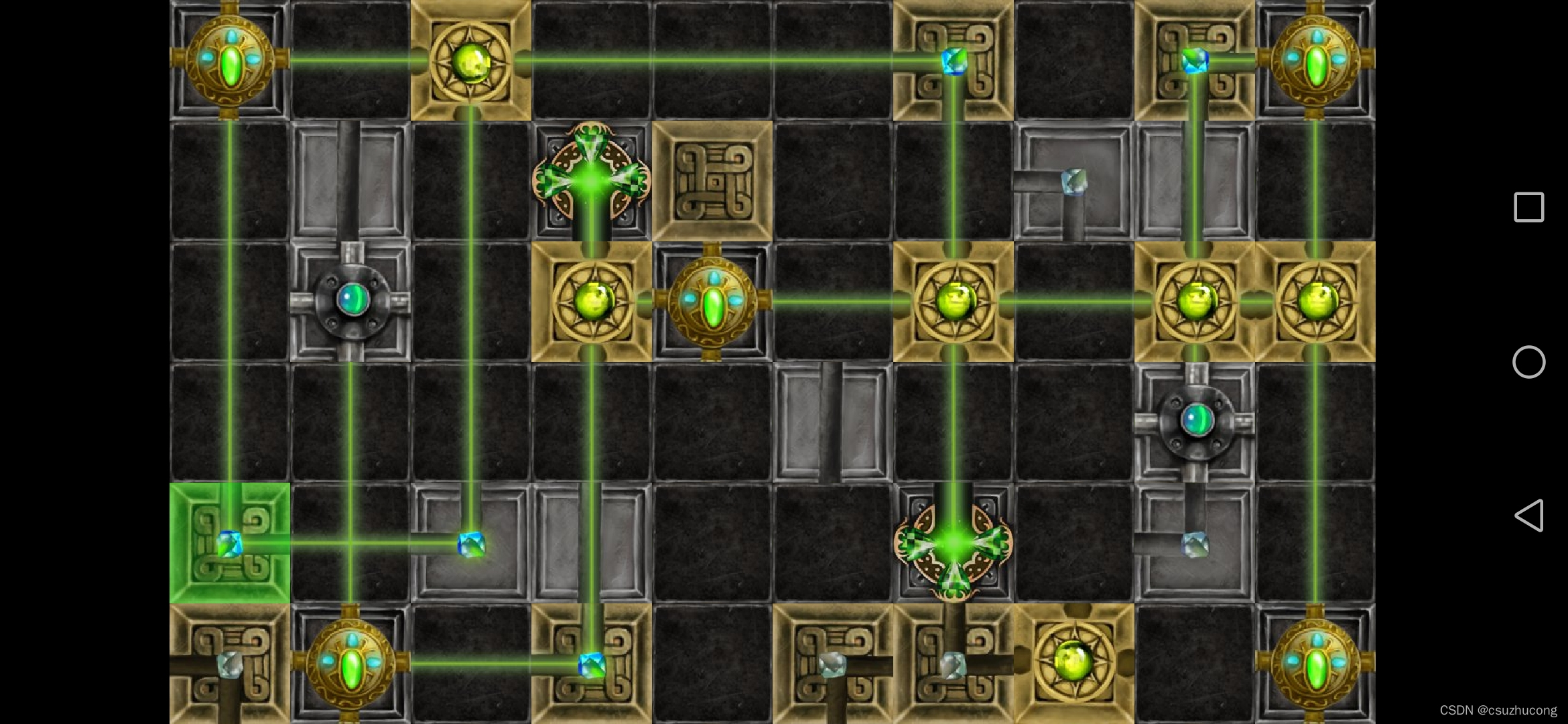
2-20

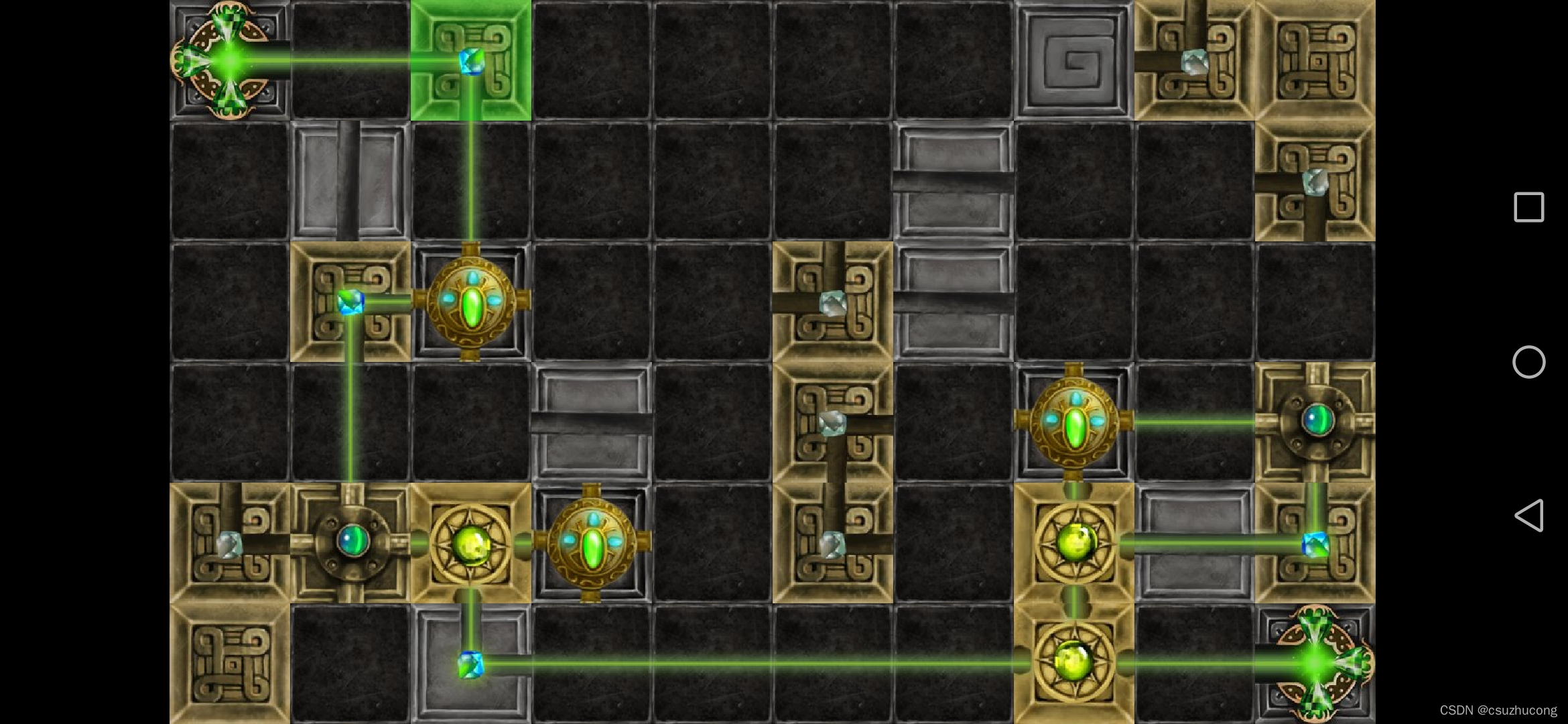
第三章

3-1

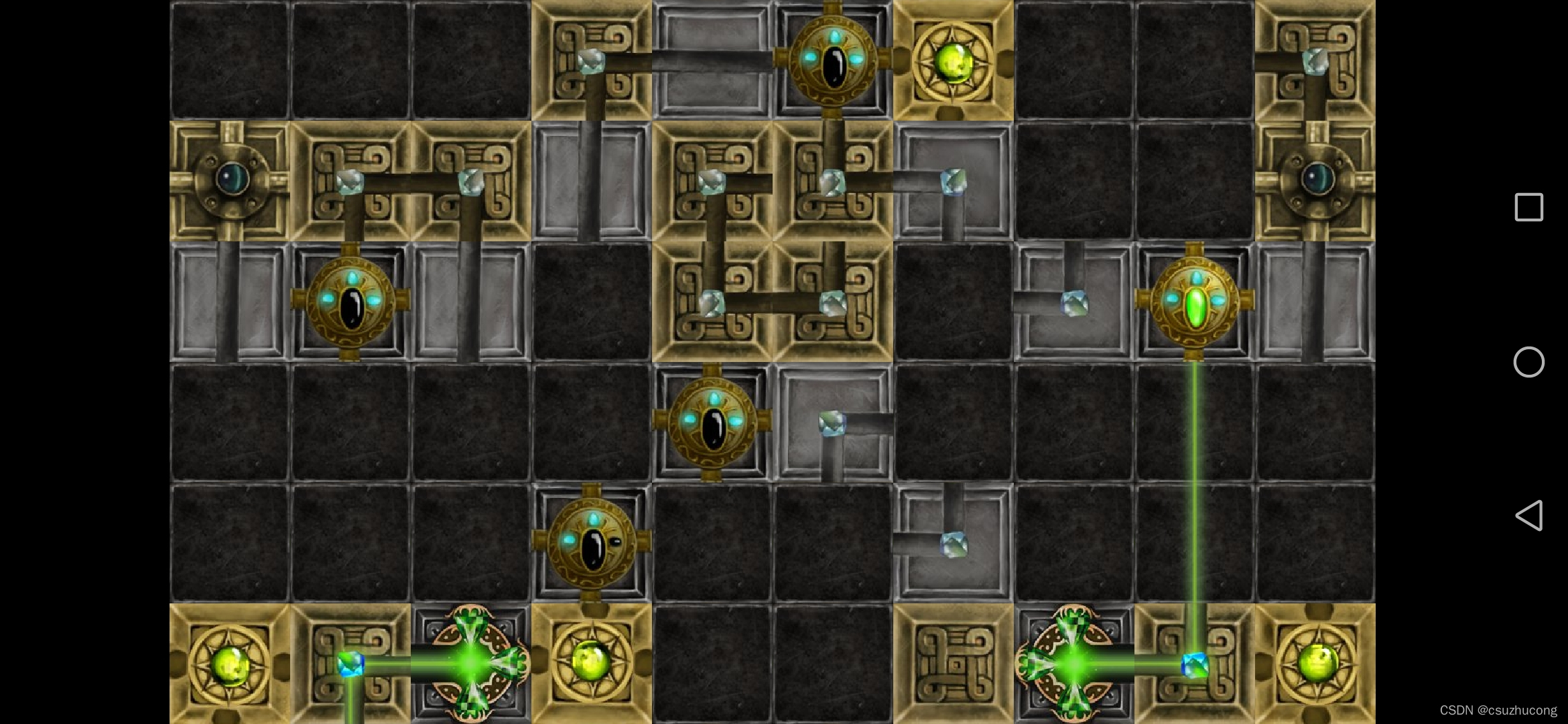
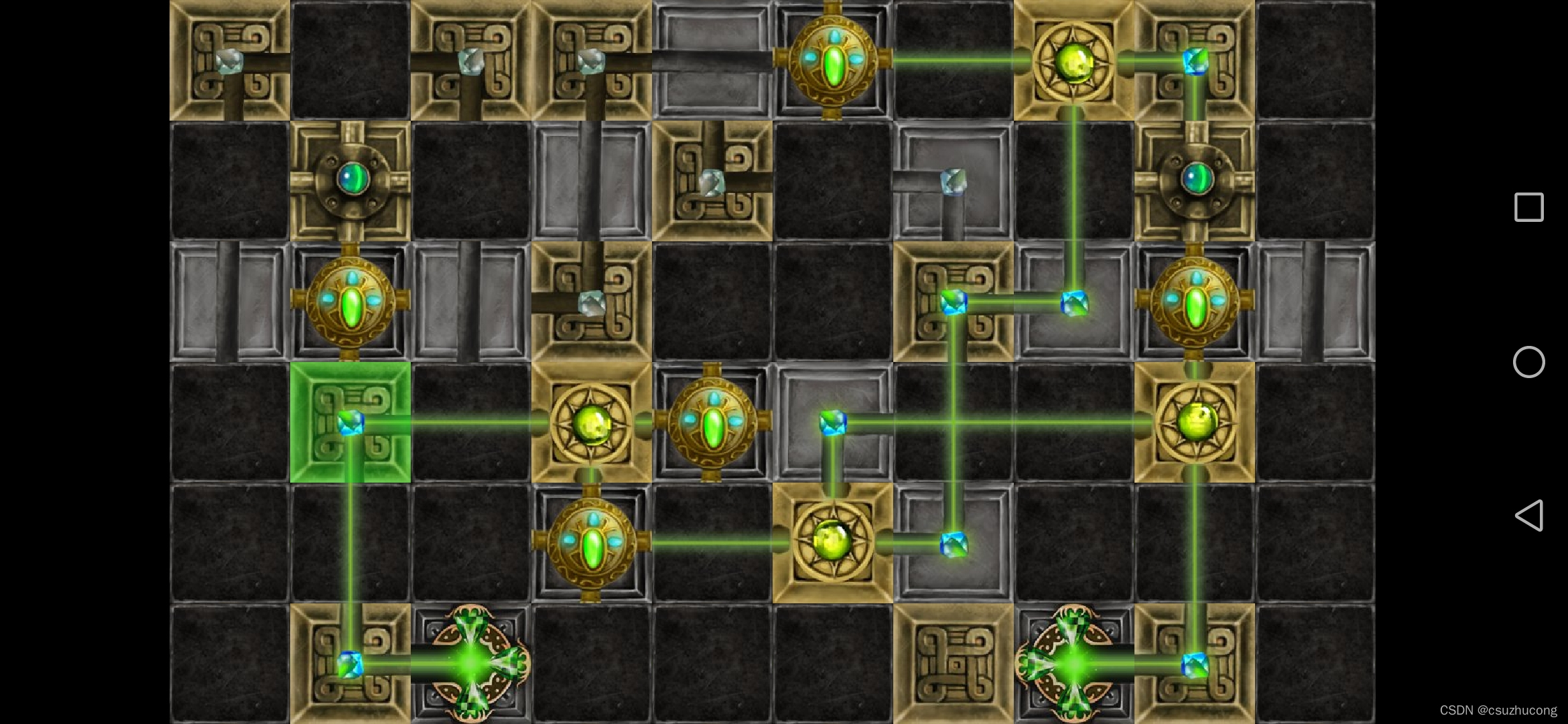
3-2

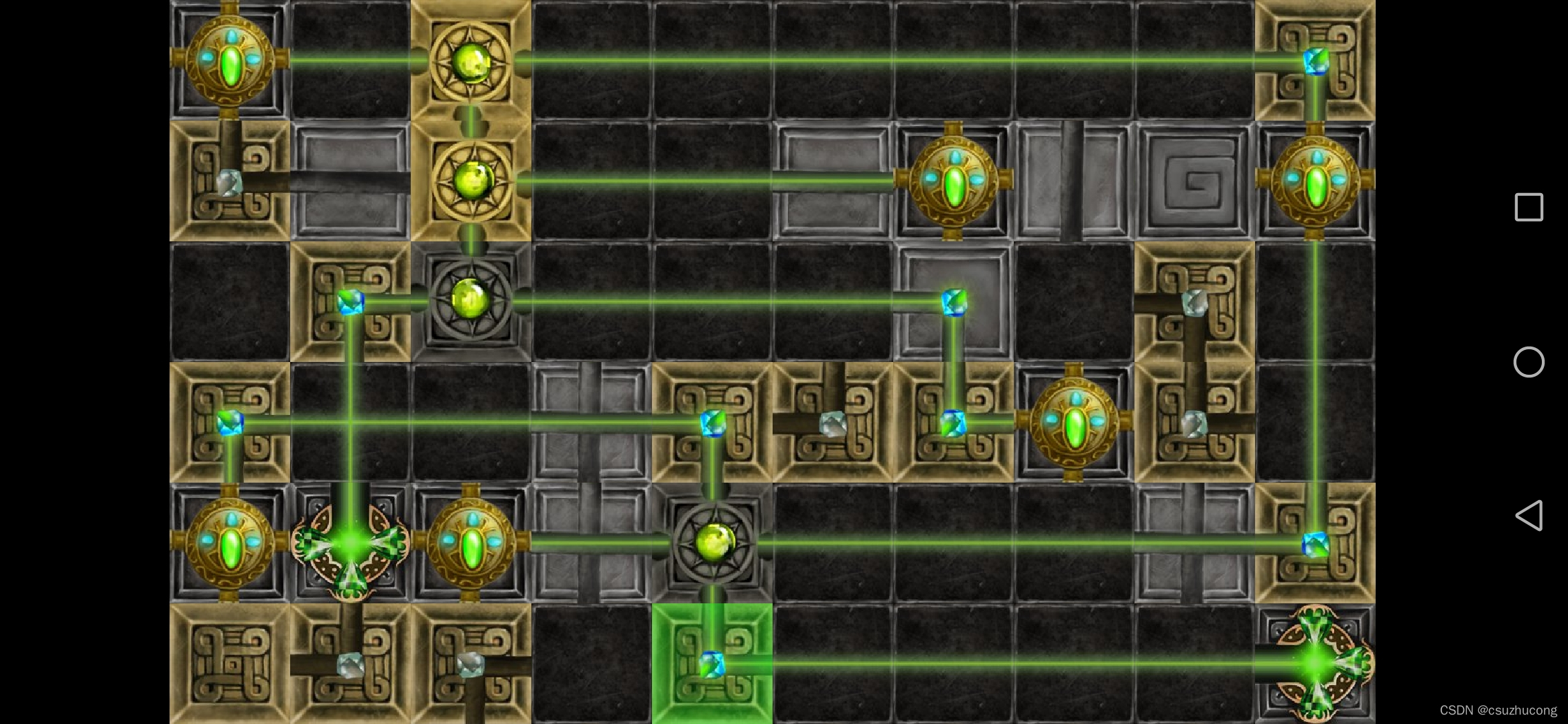
3-3

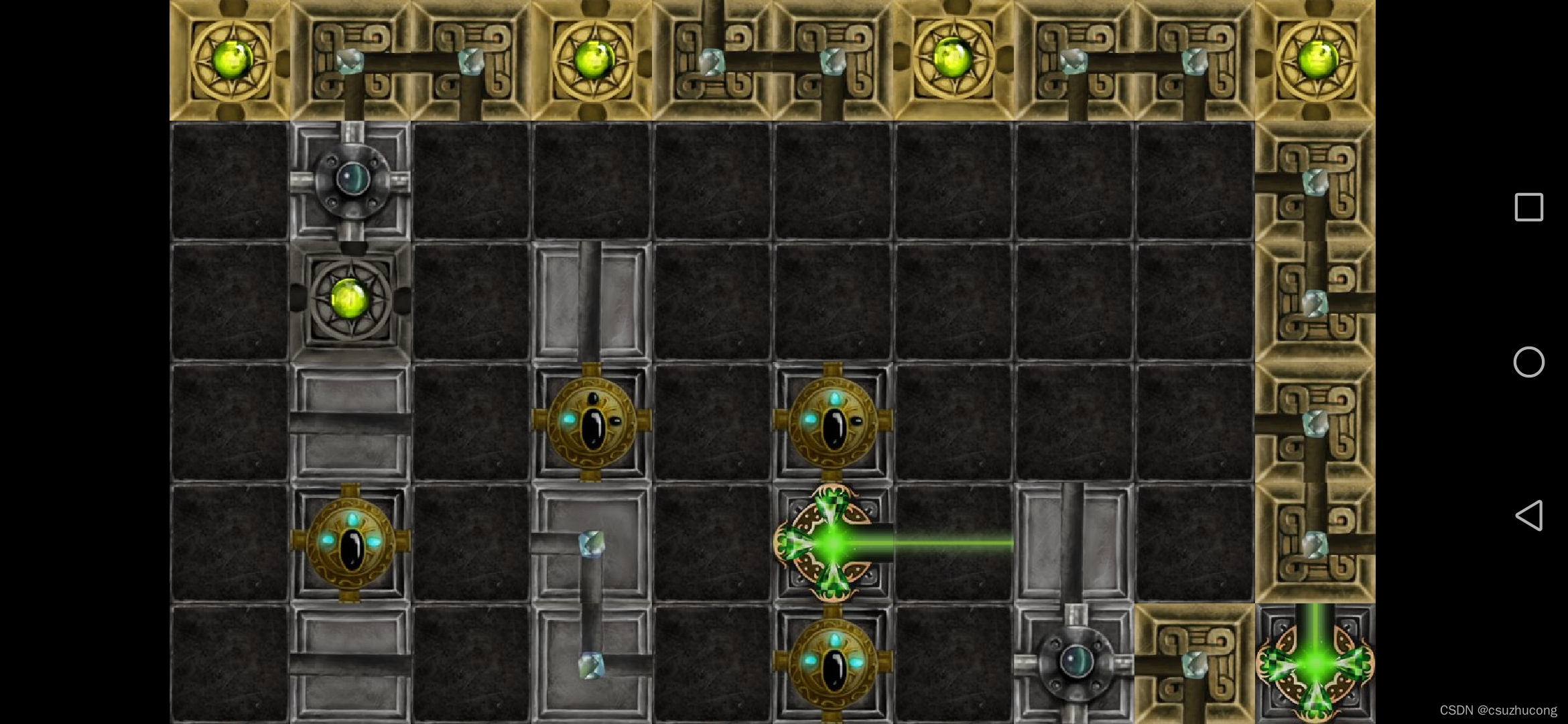
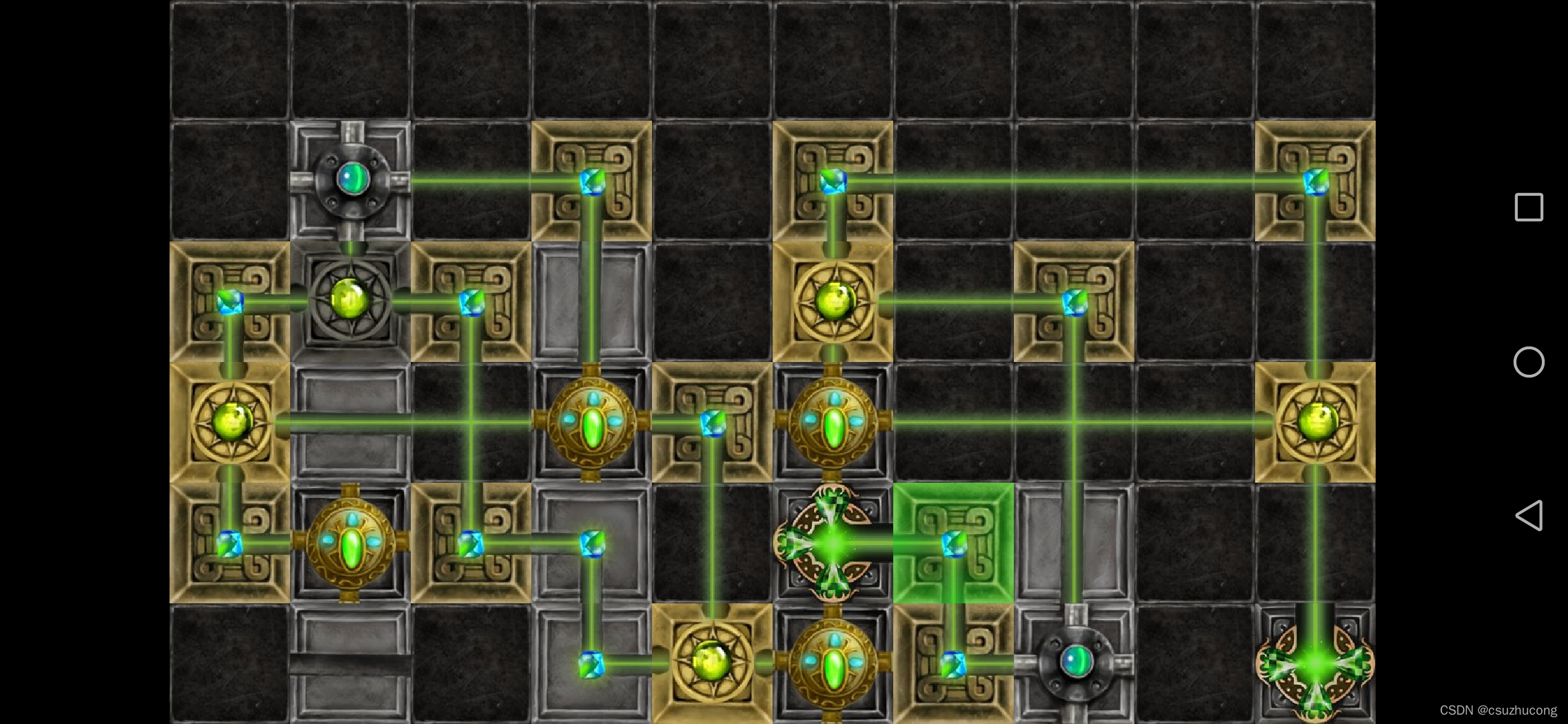
3-4

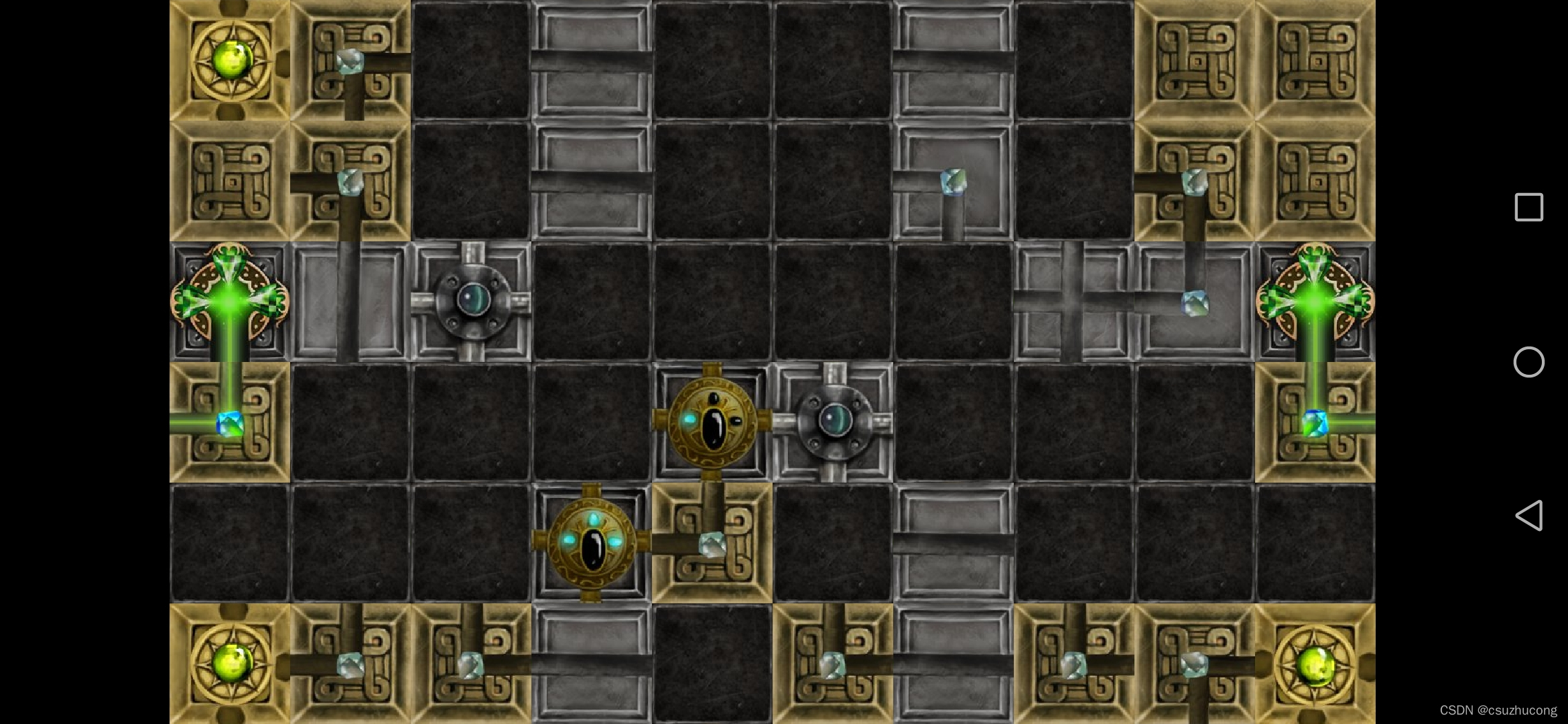
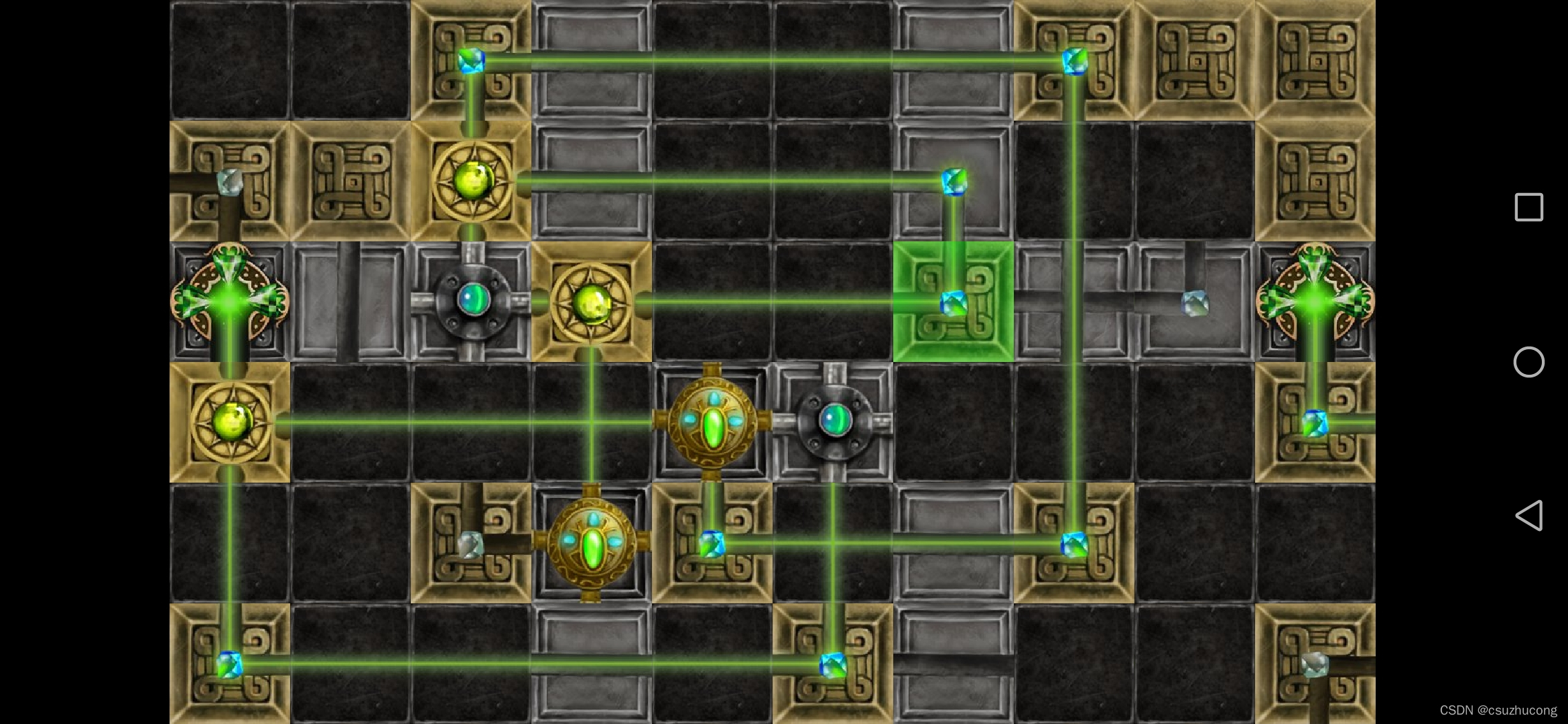
3-5

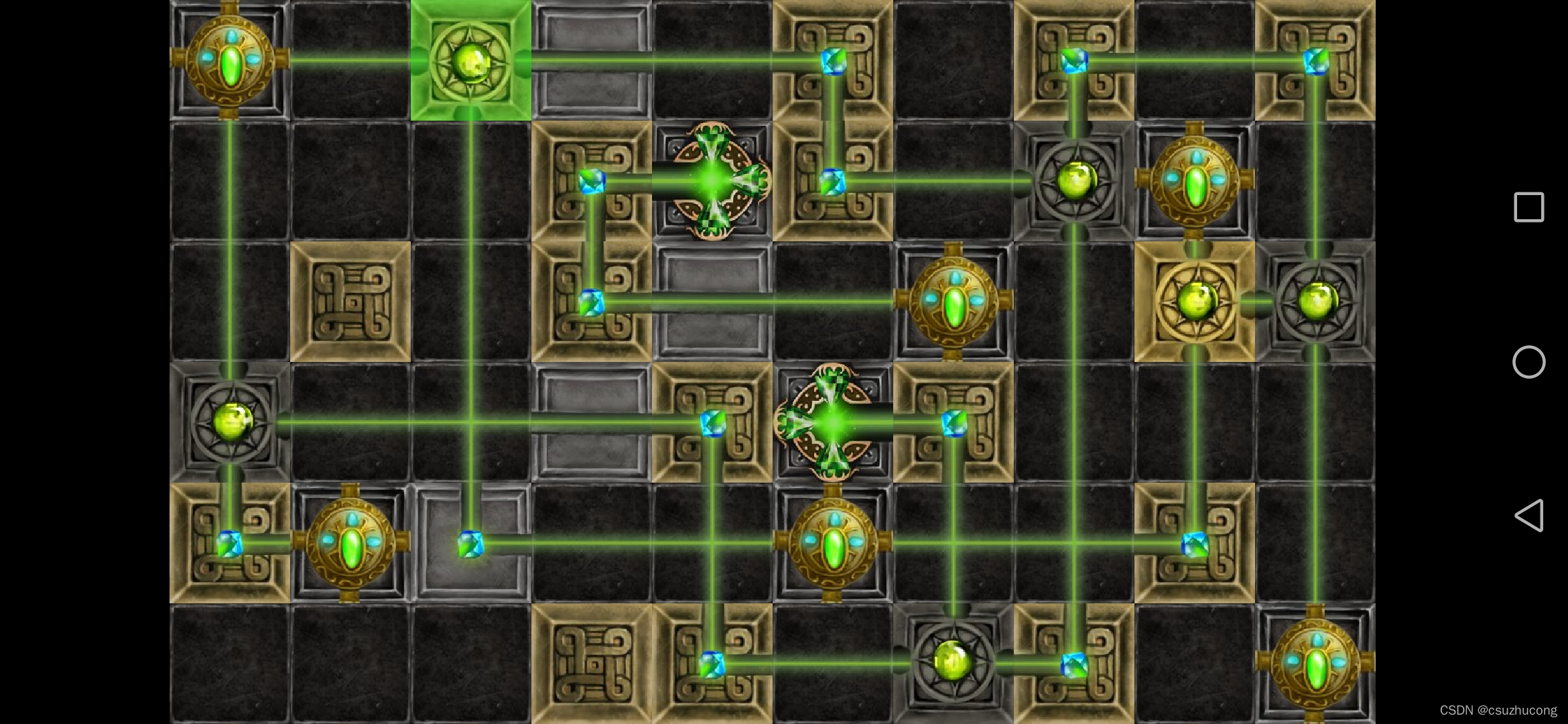
 3-6

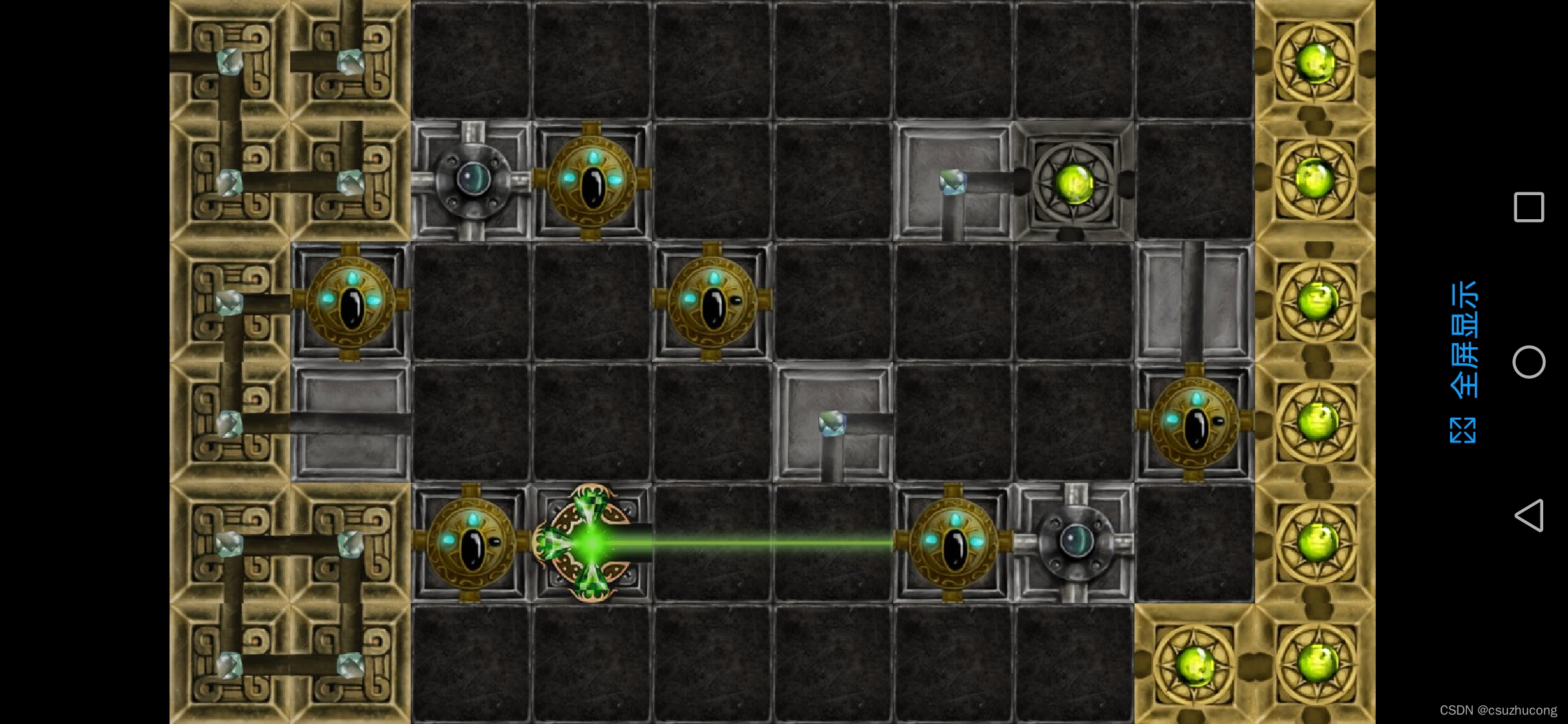
3-7

有一个解法只要去掉一个砖头就可以了：

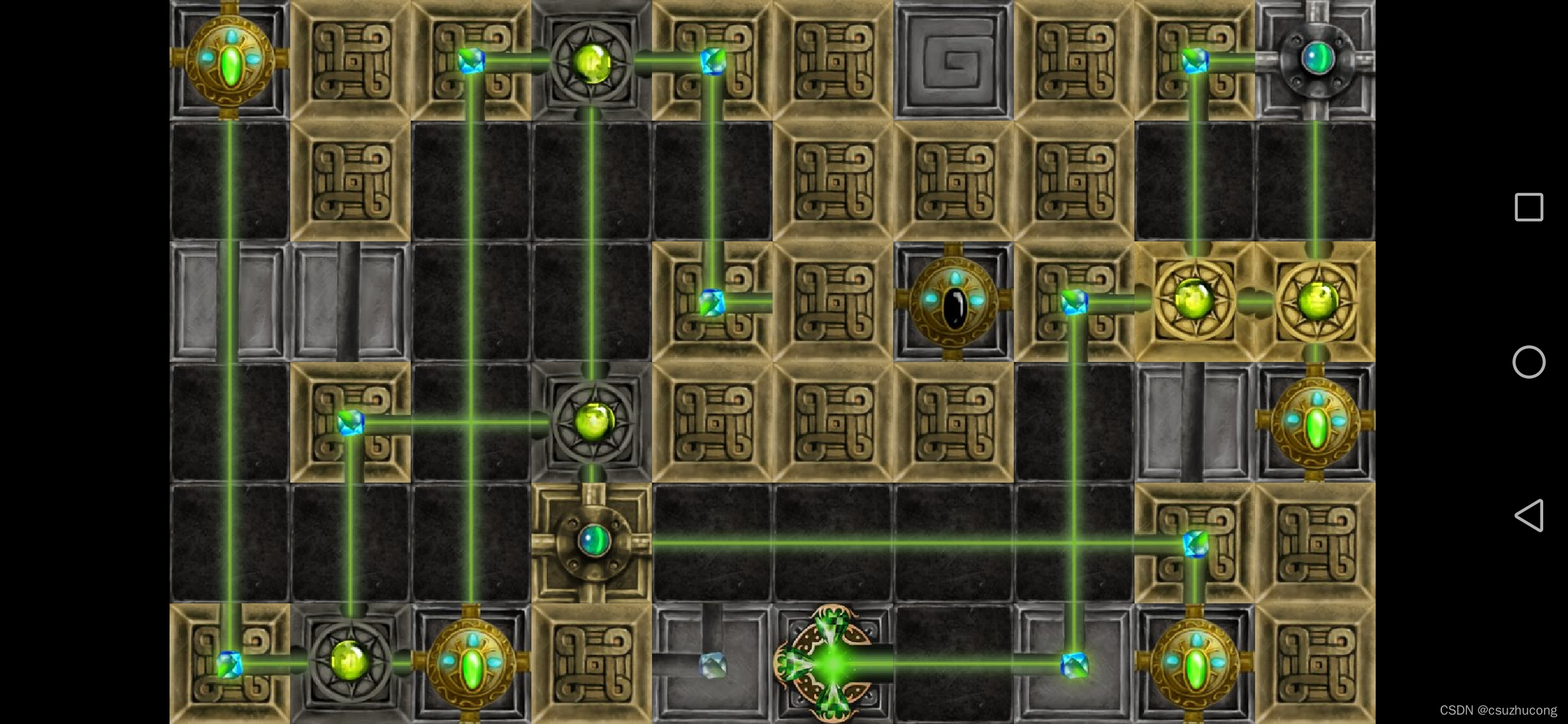
 正确解法：

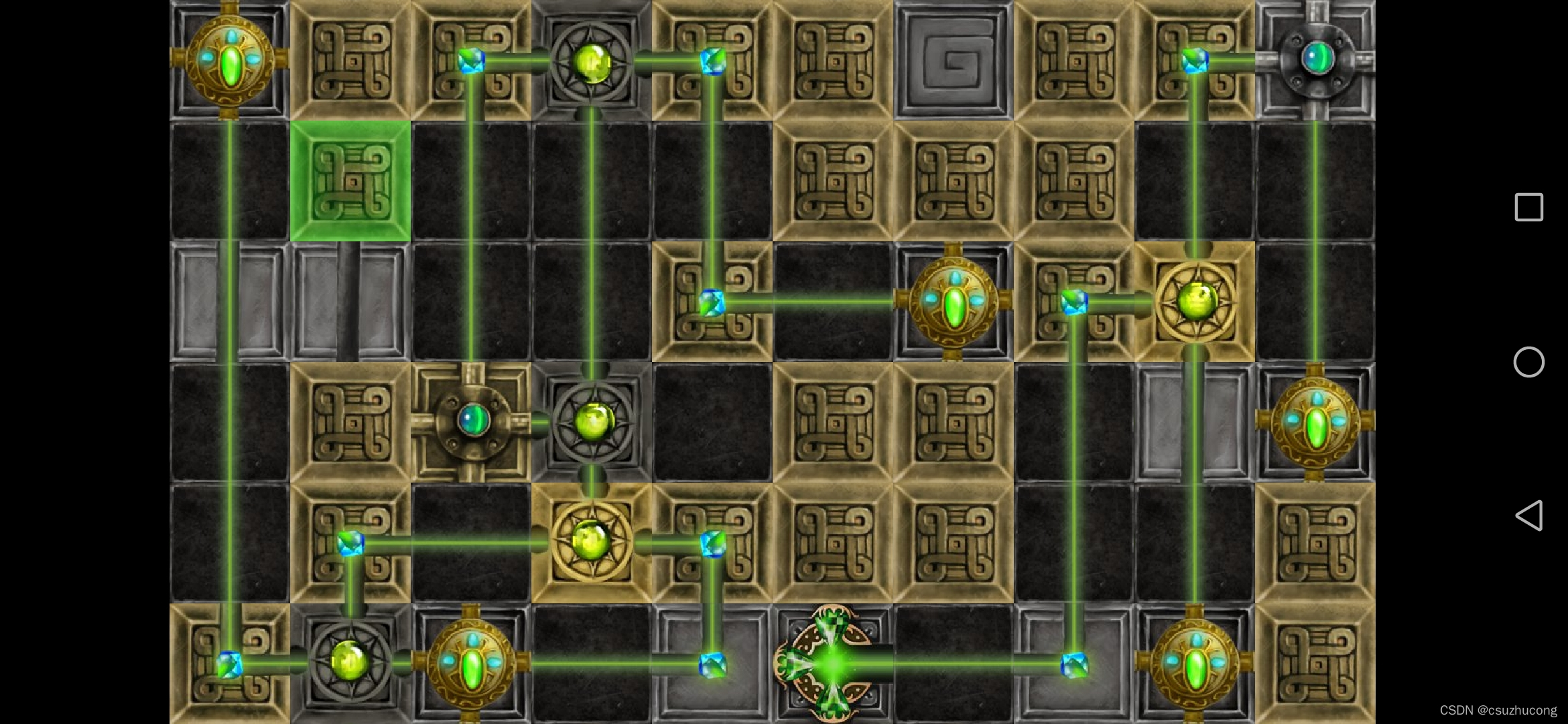
3-8

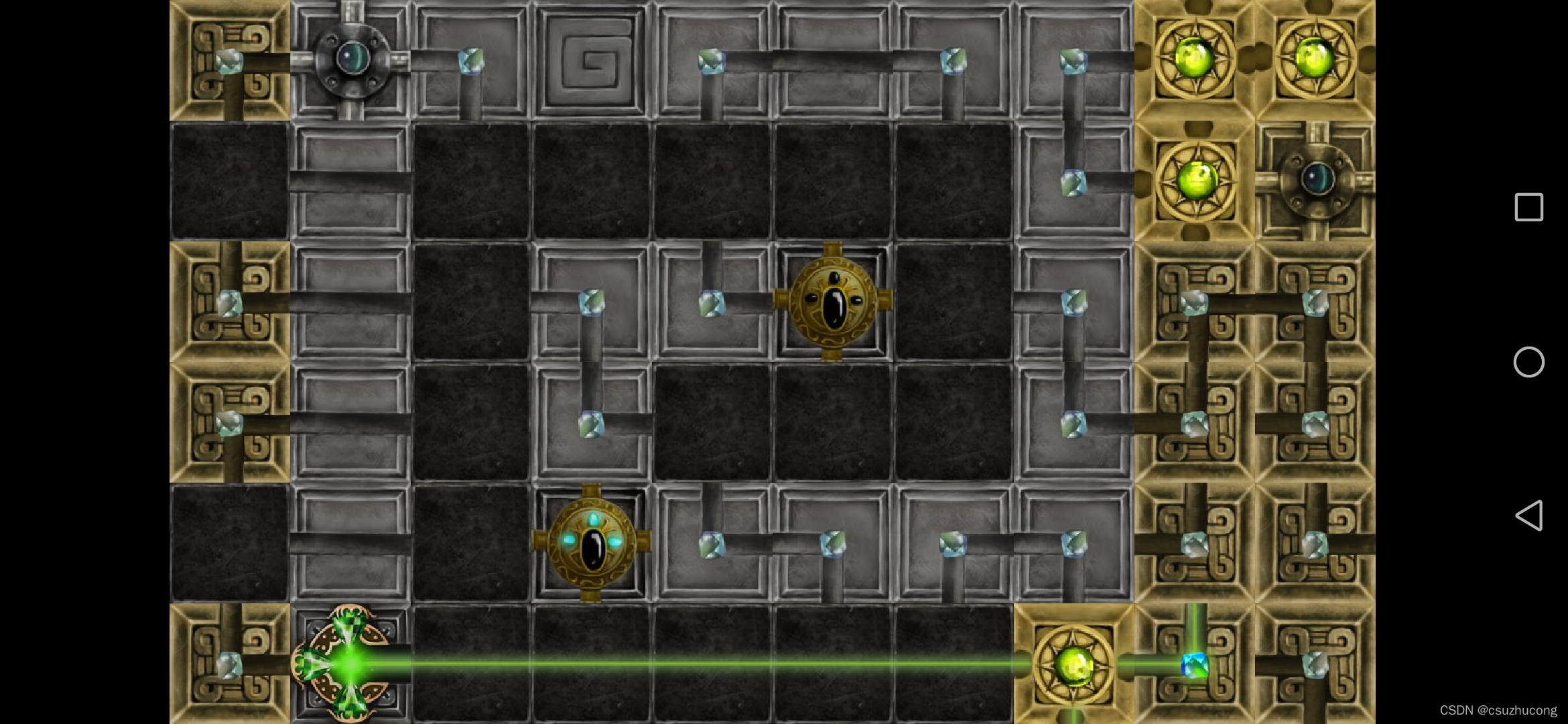
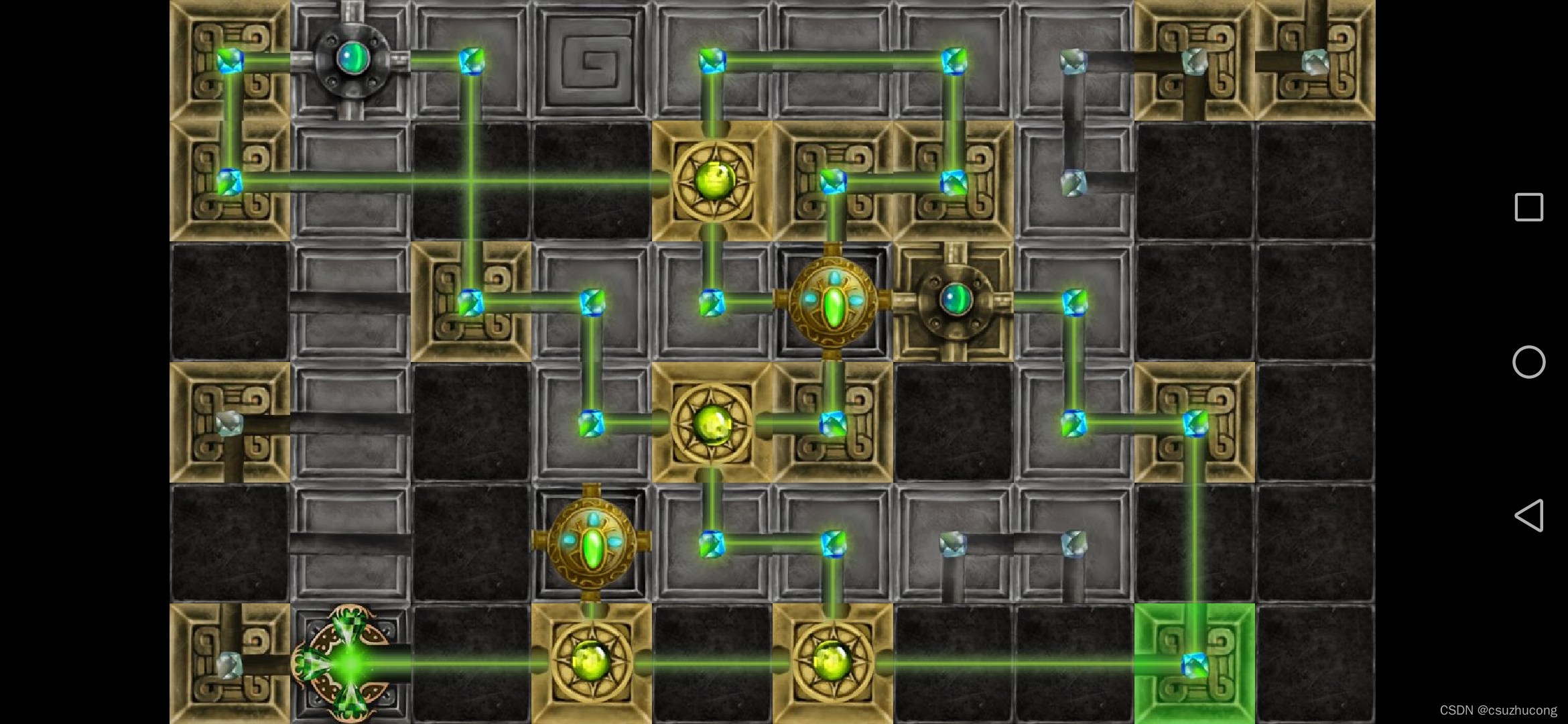
3-9

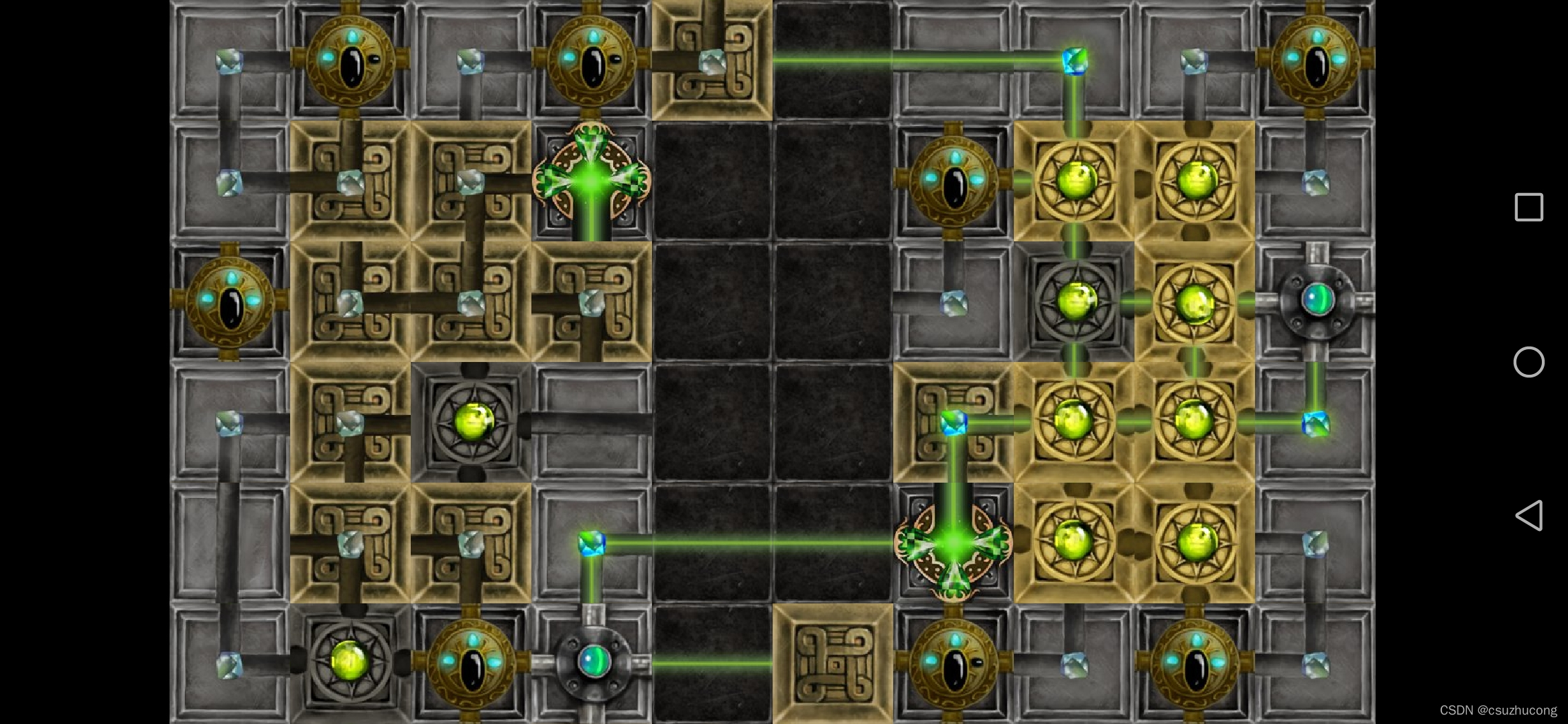
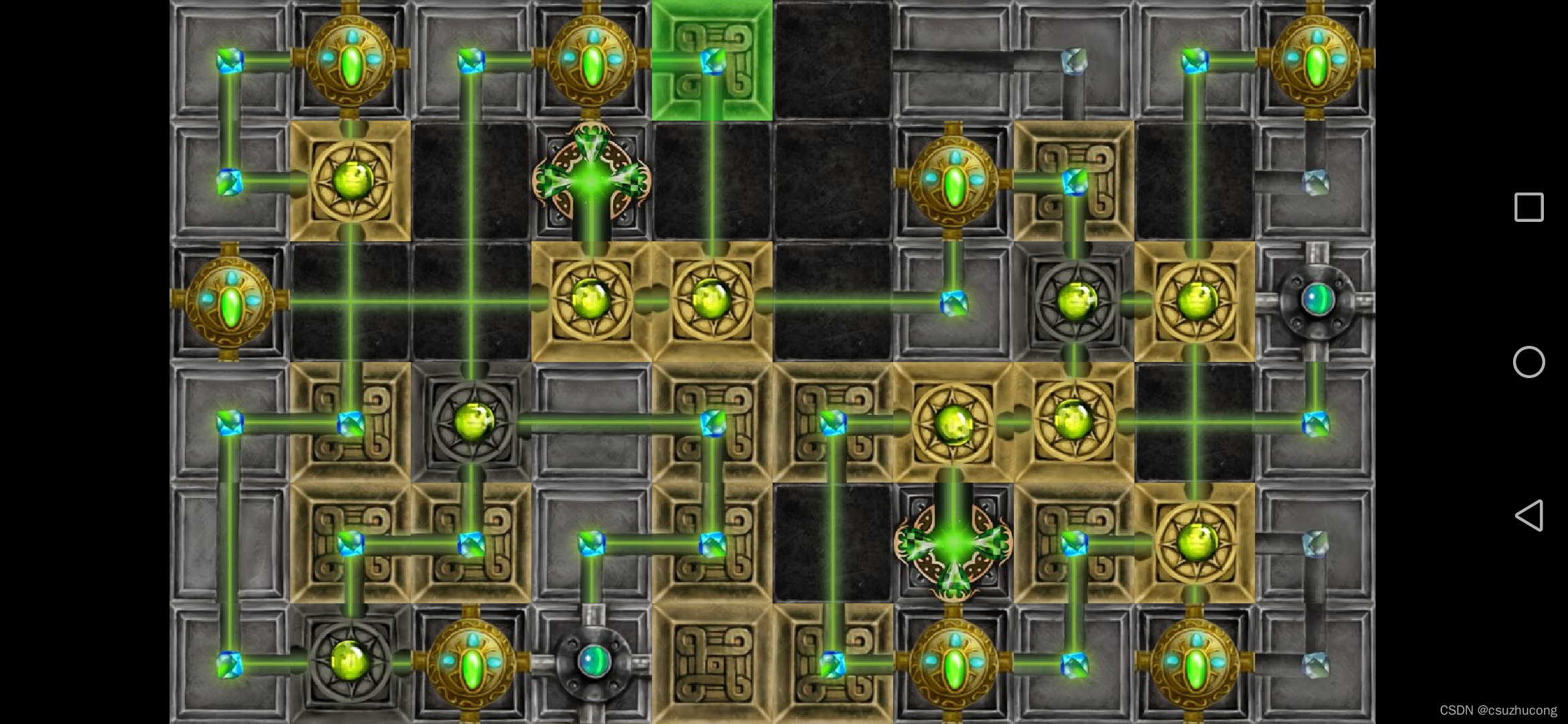
3-10

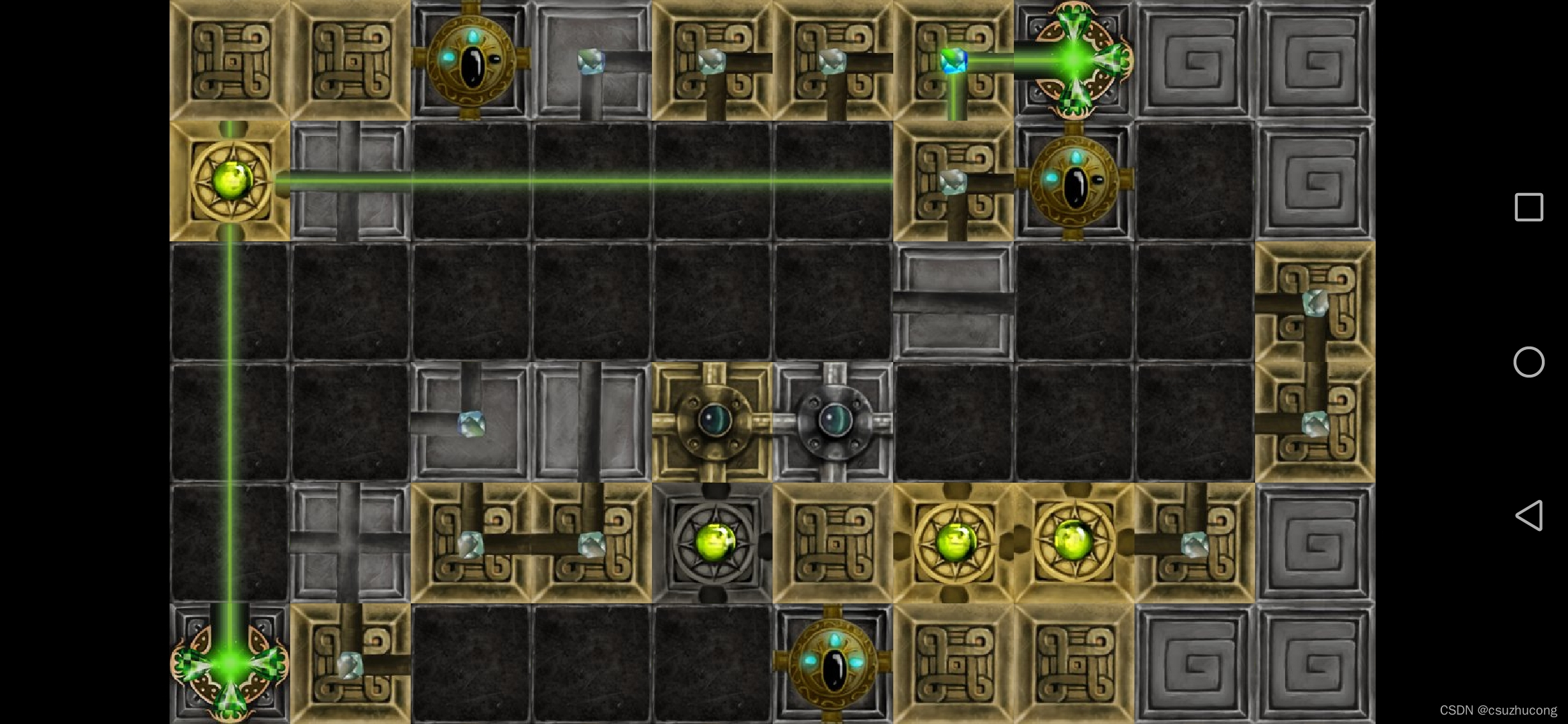
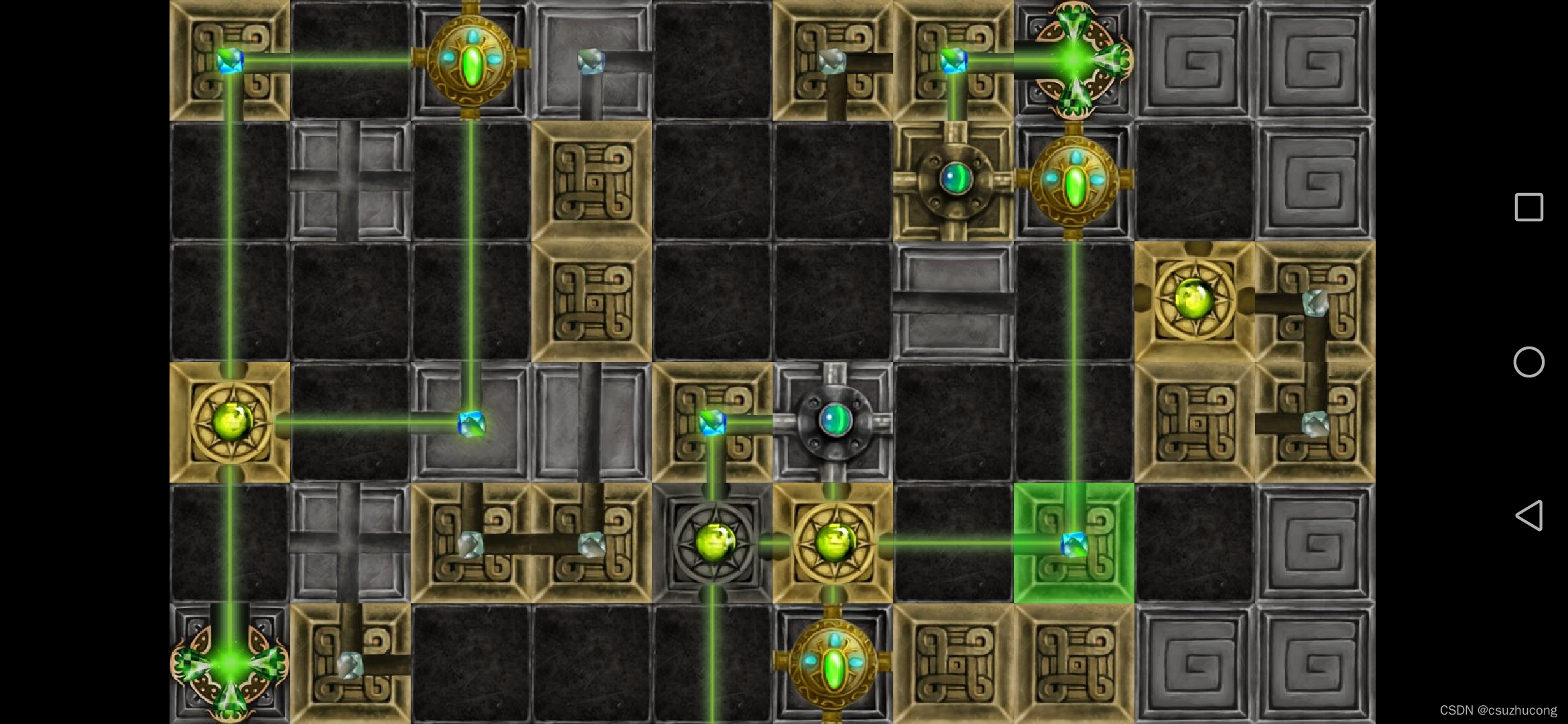
3-11

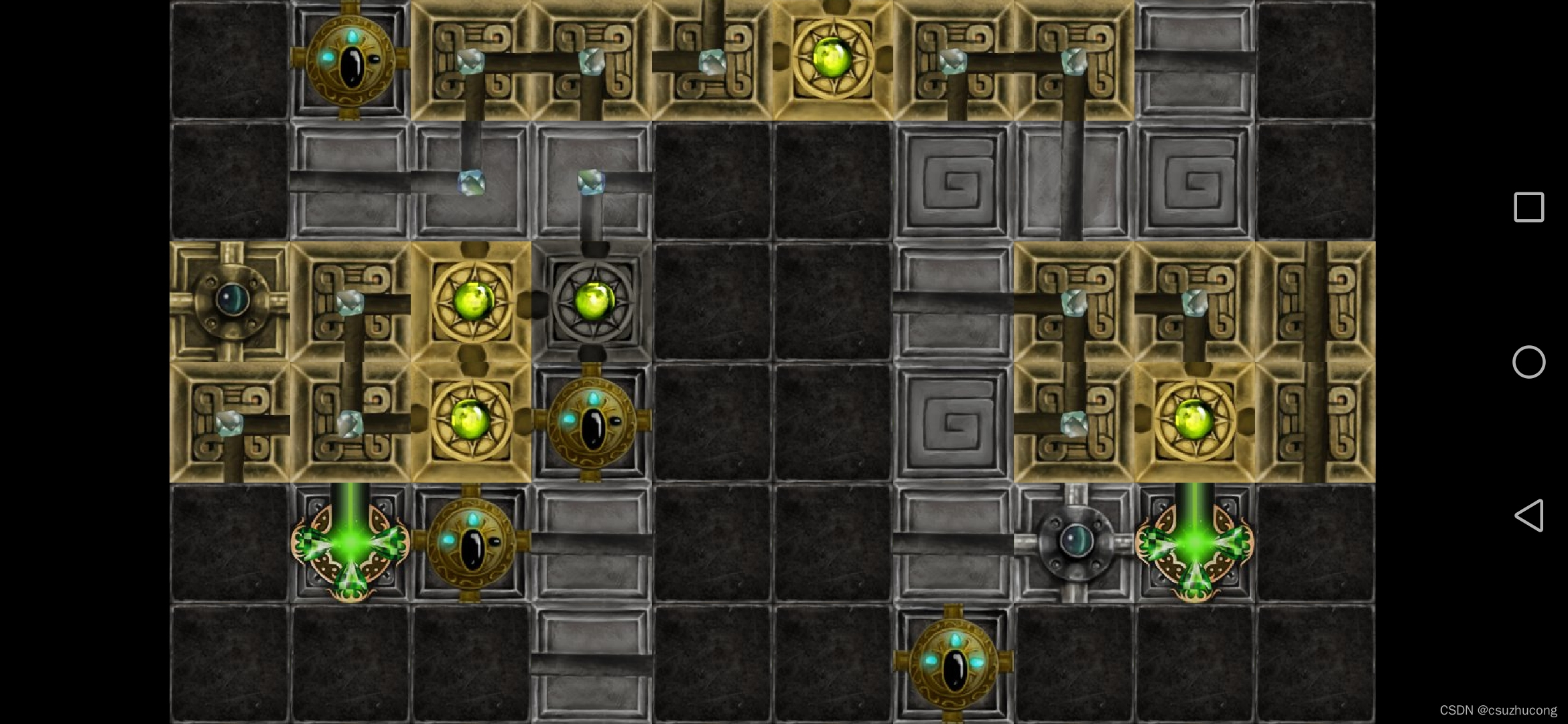
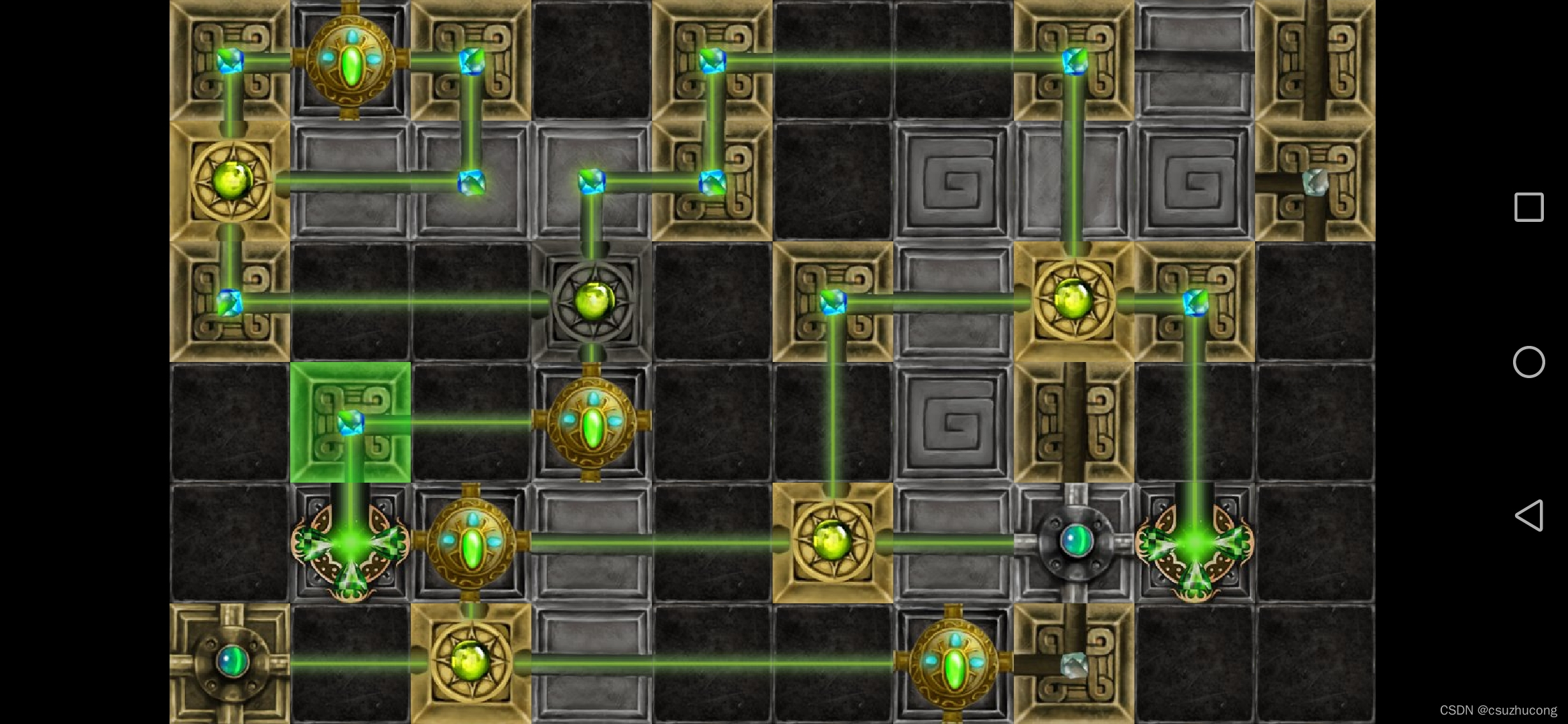
 3-12

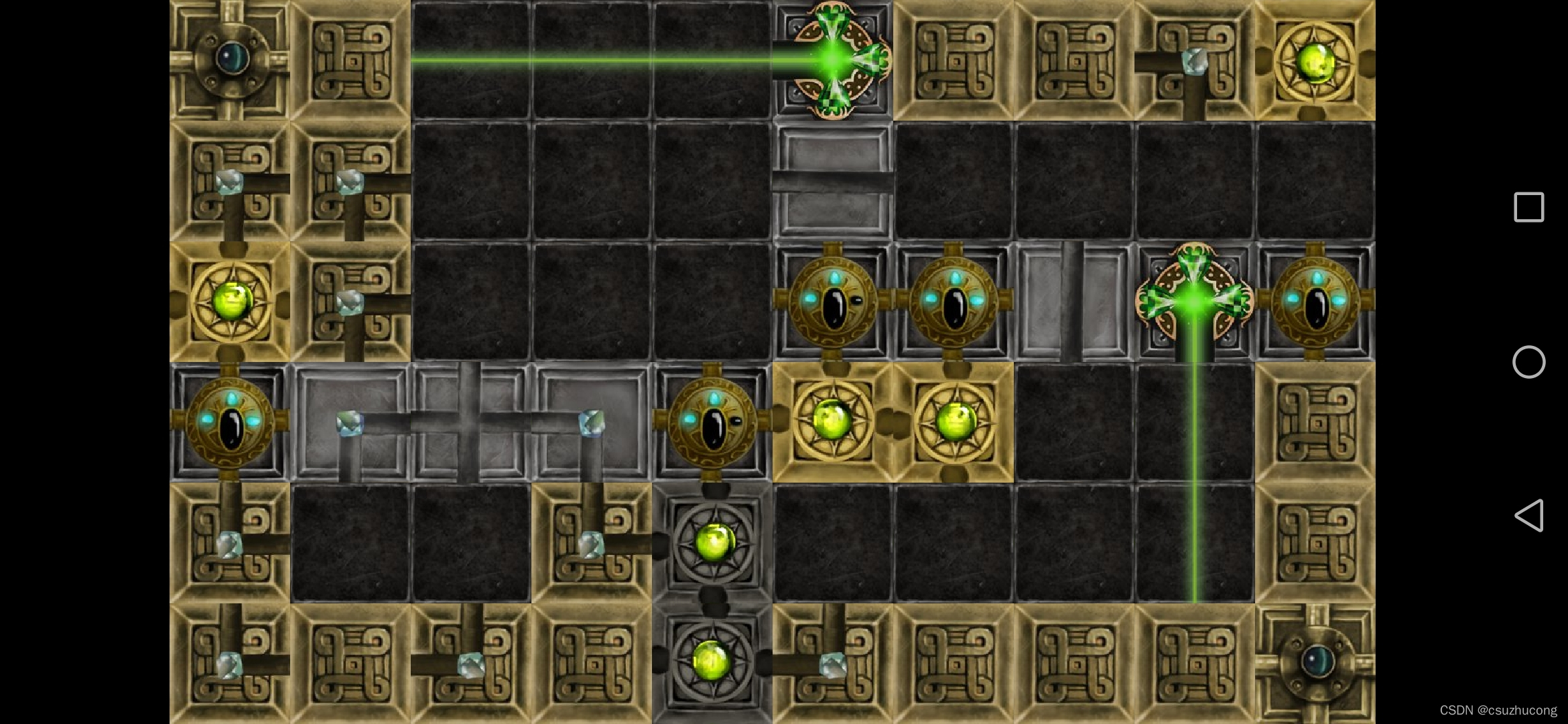
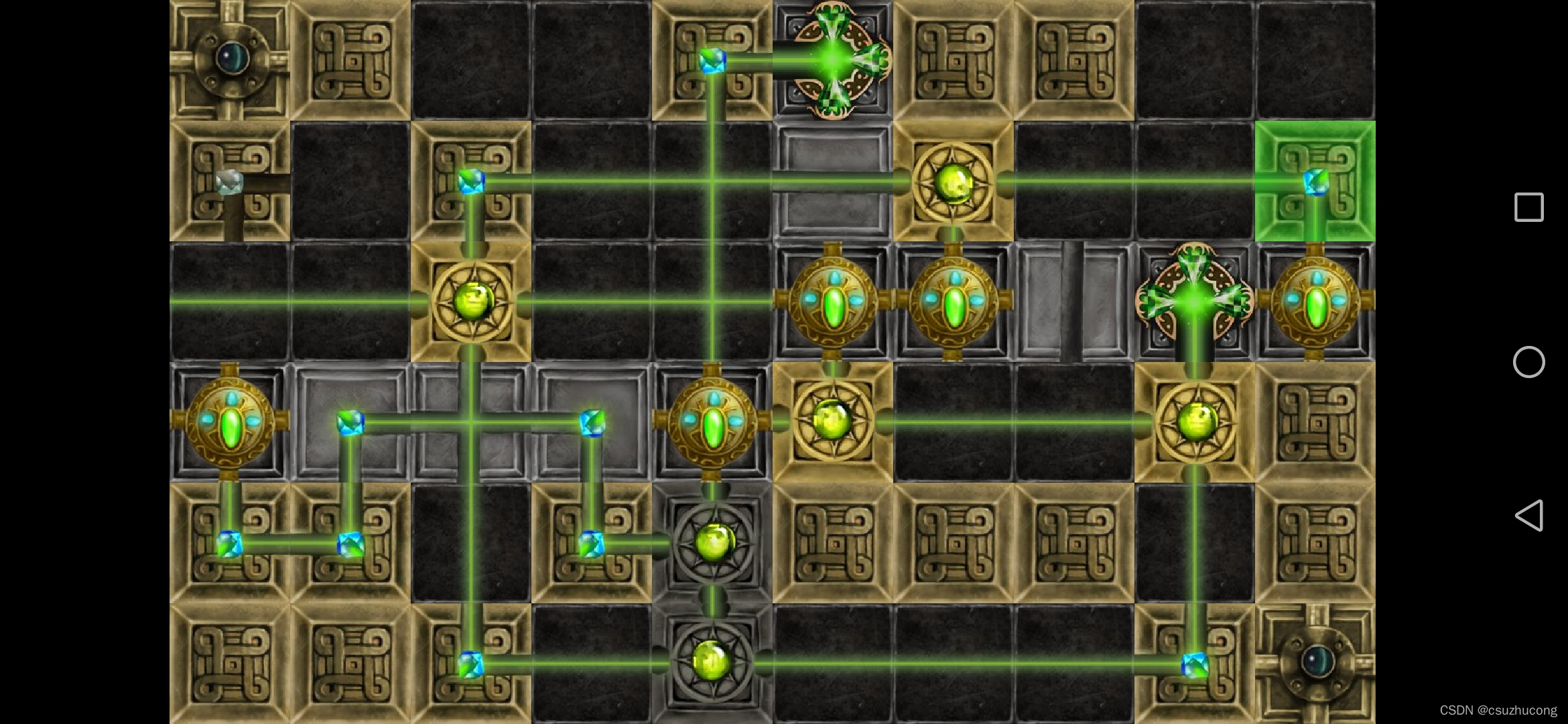
3-13

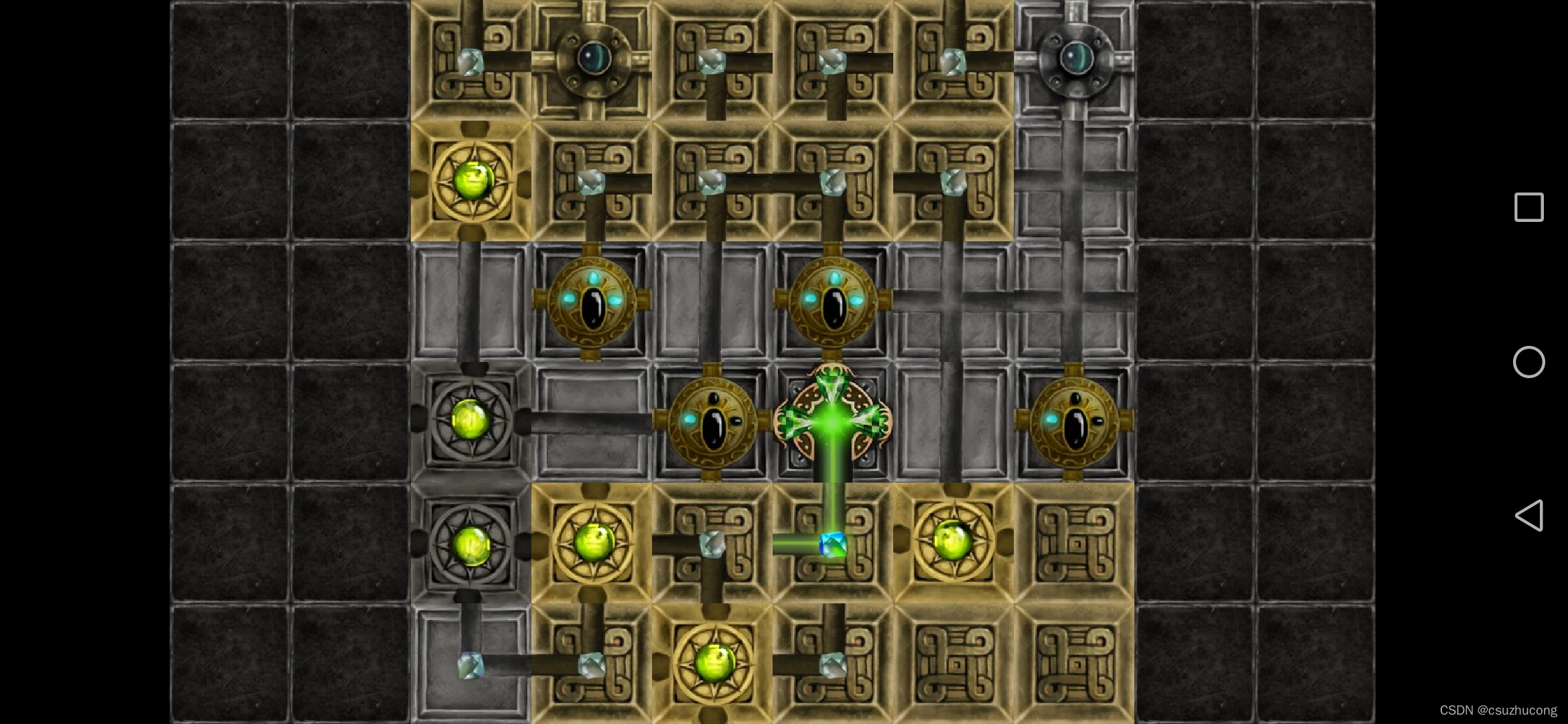
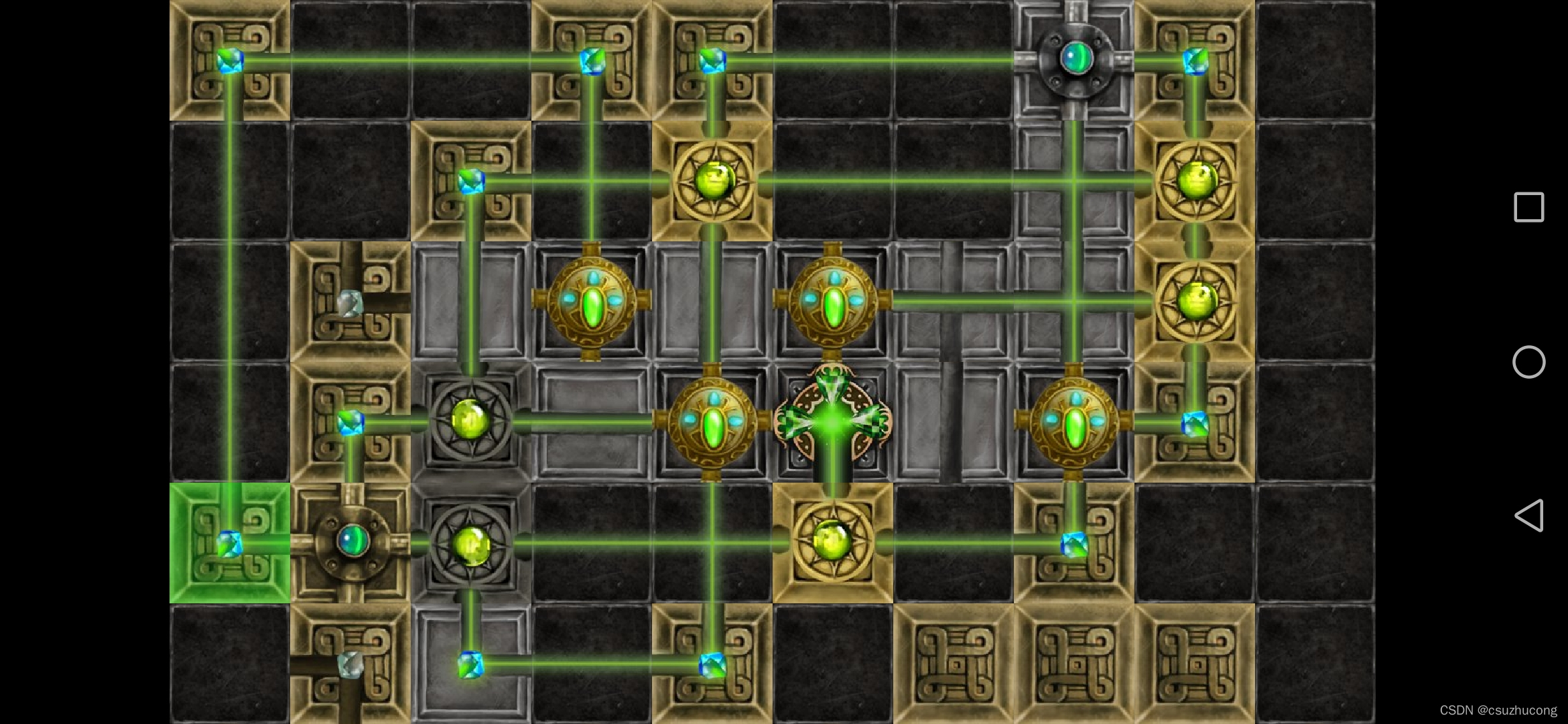
3-14

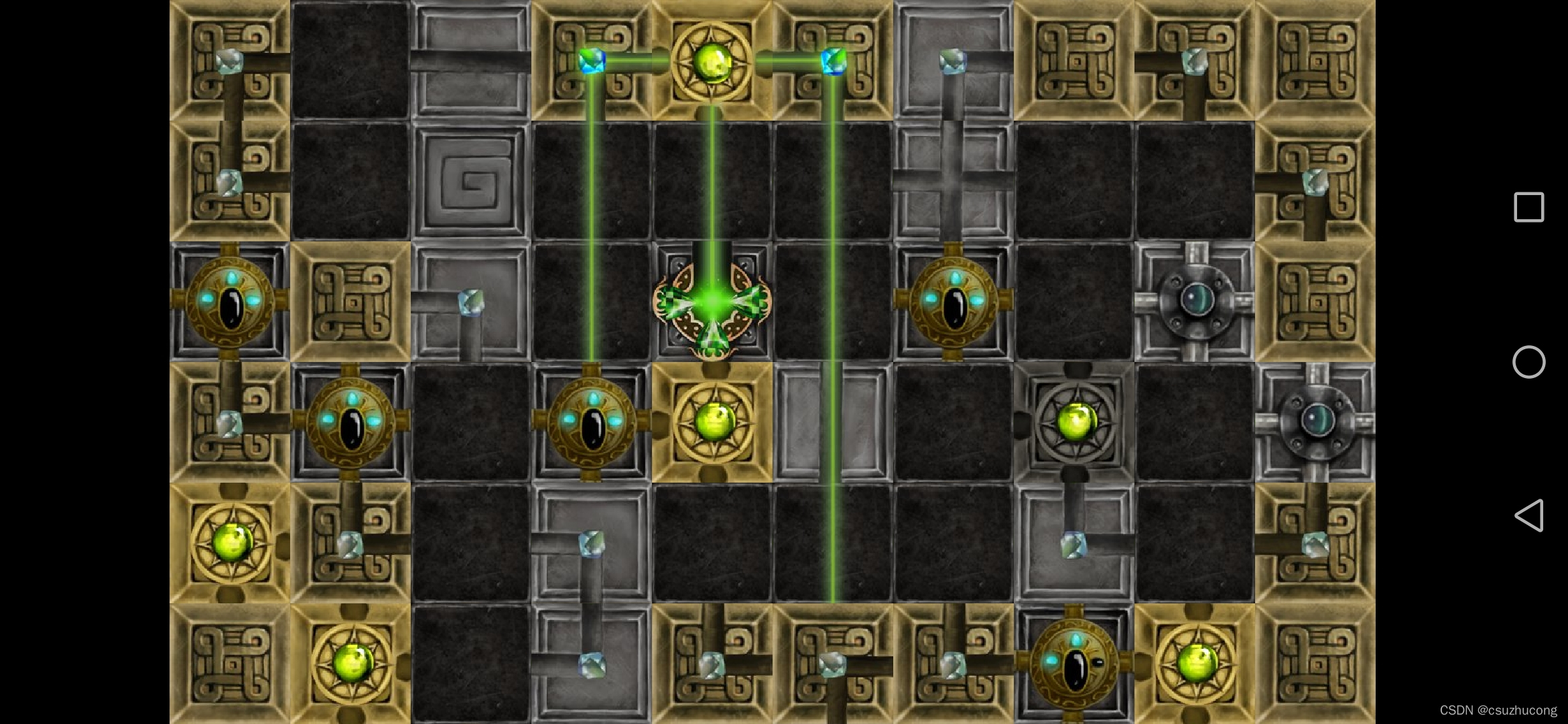
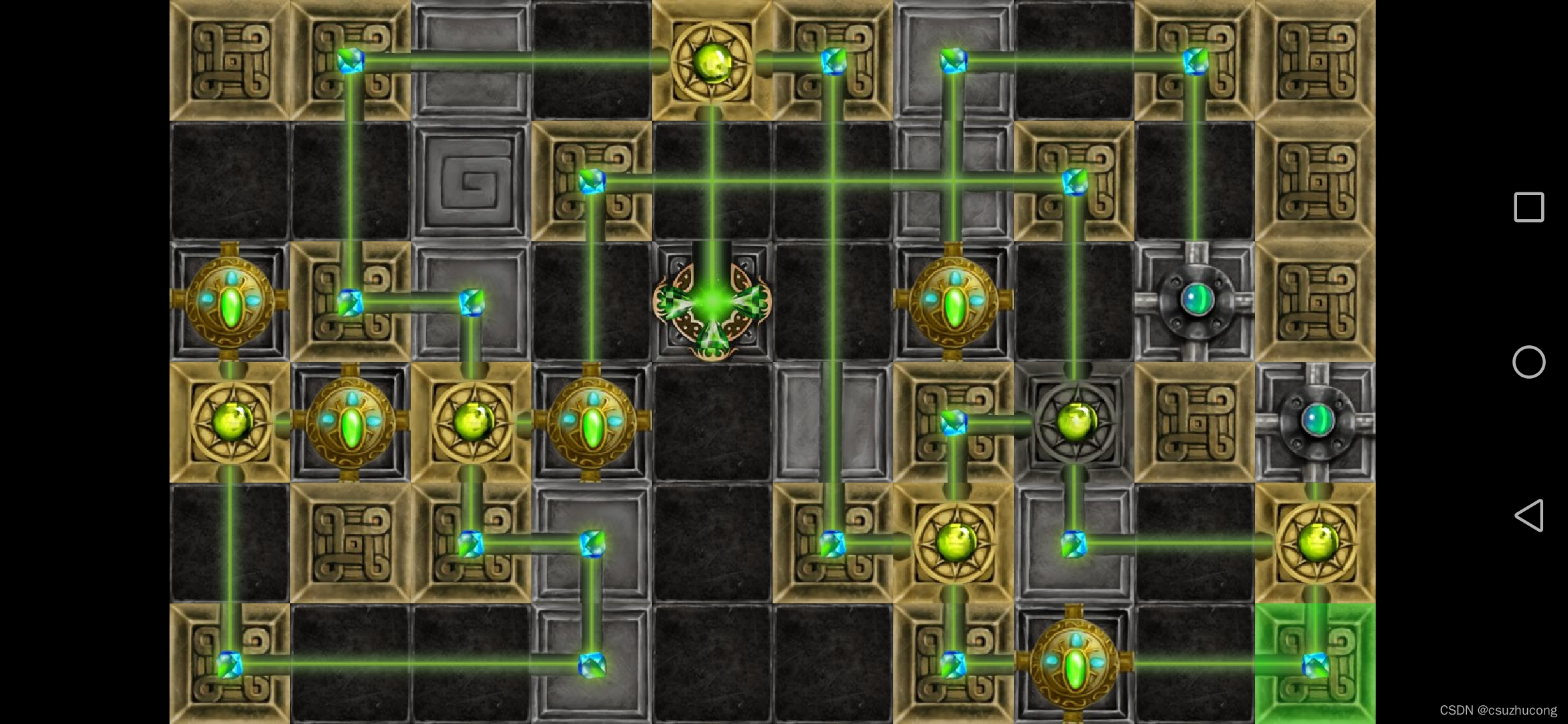
3-15

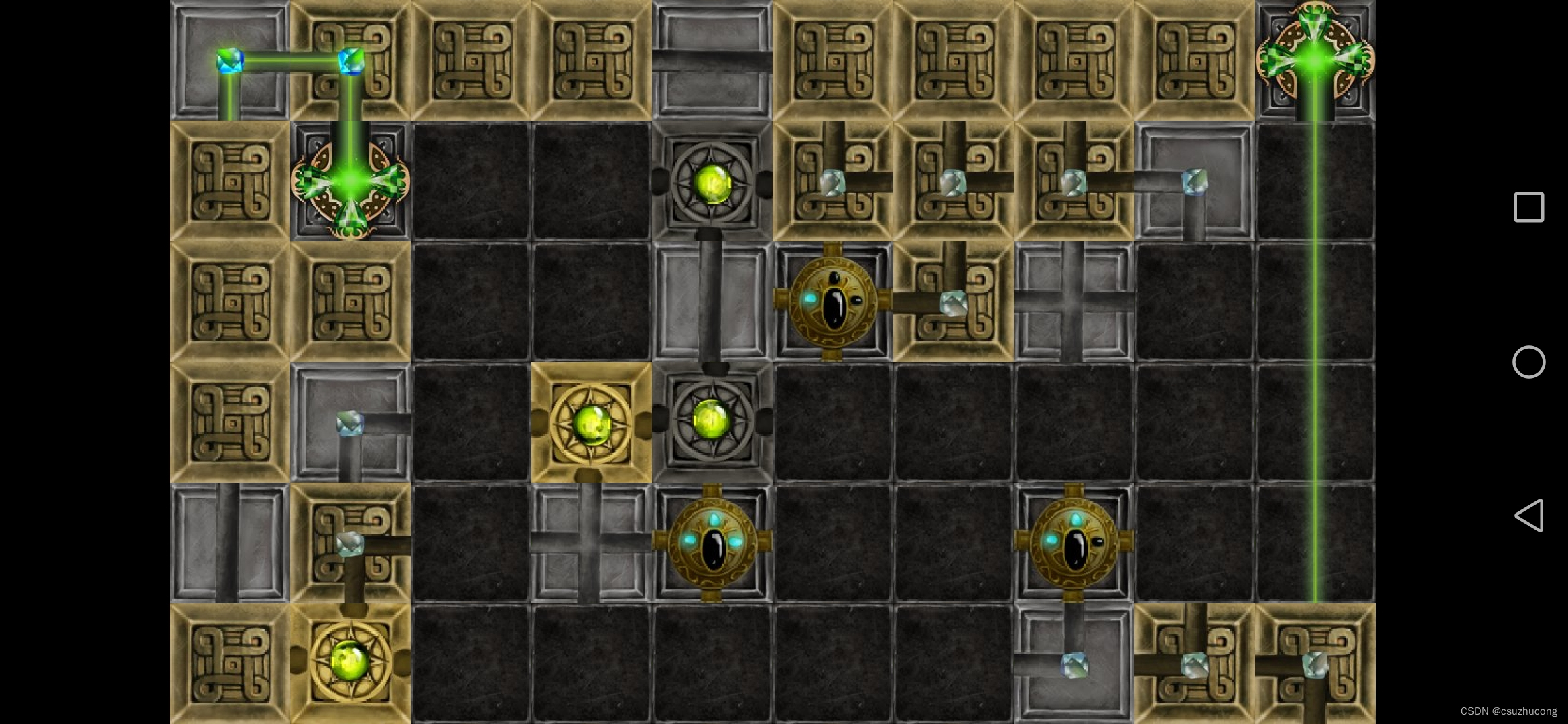
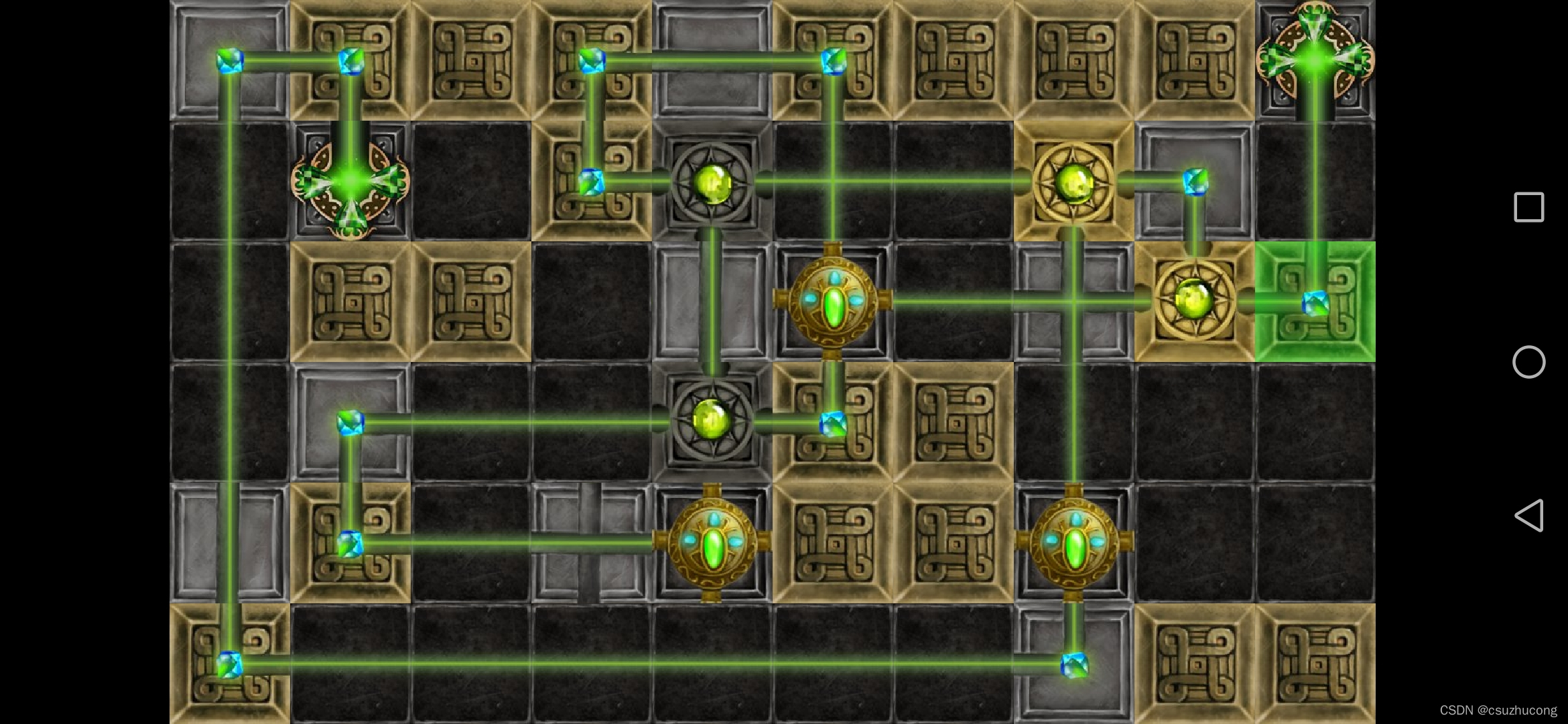
3-16

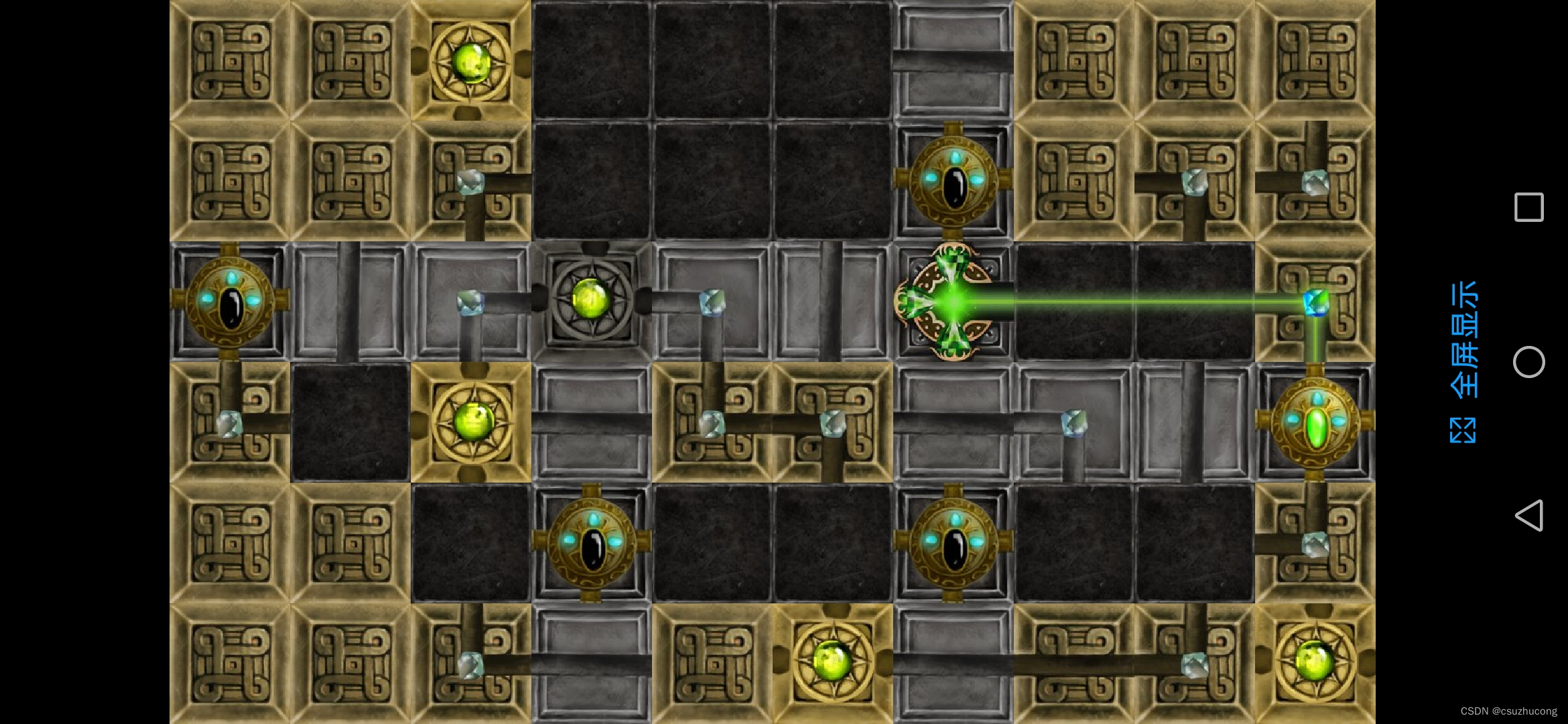
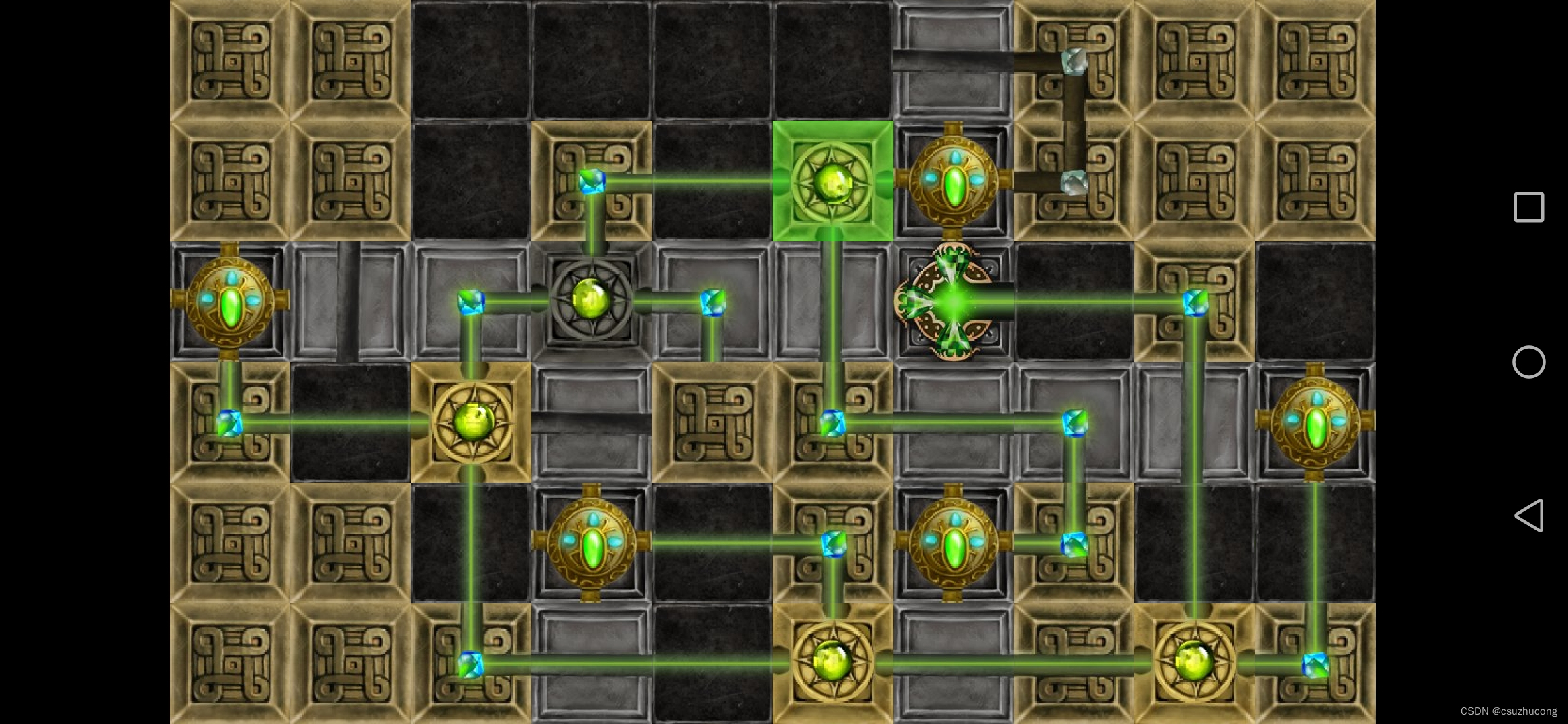
3-17

 

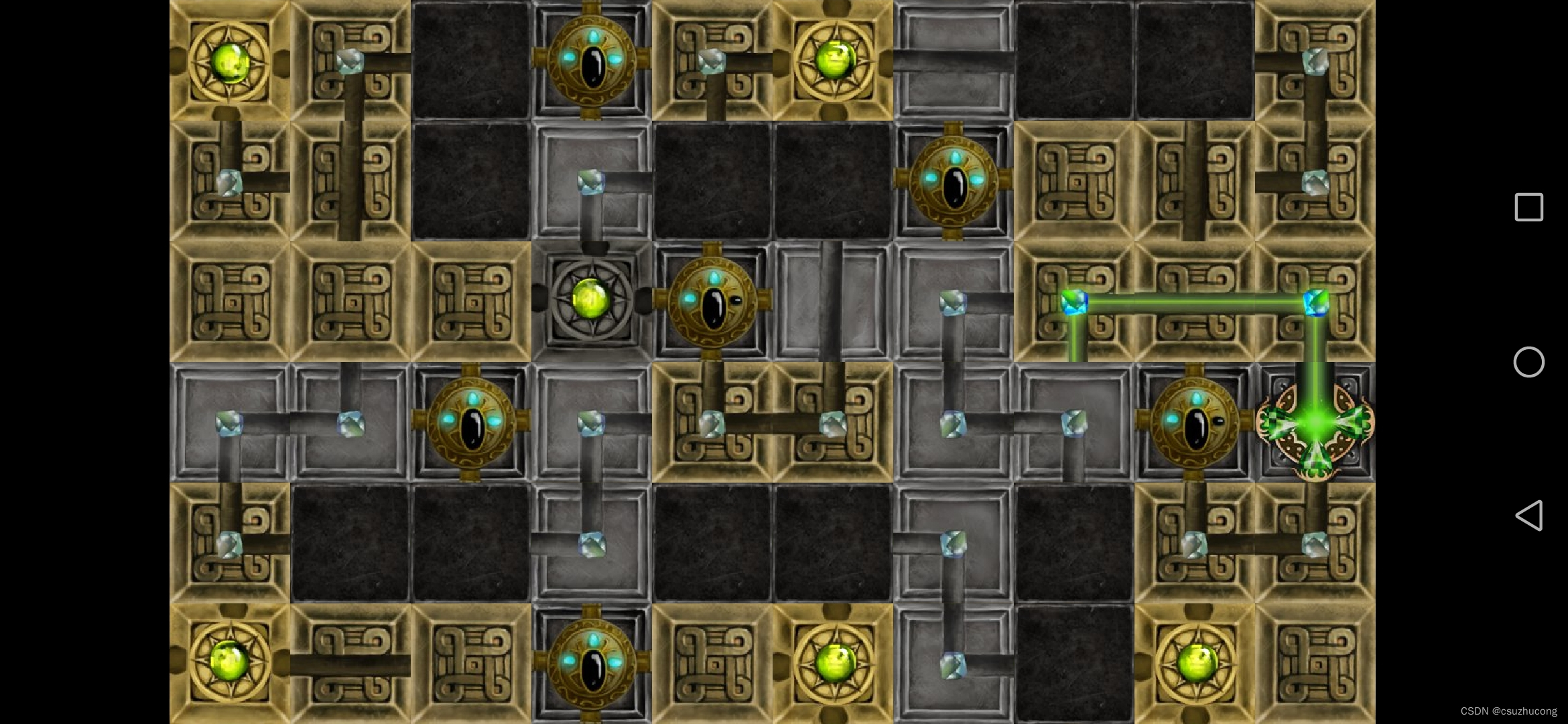
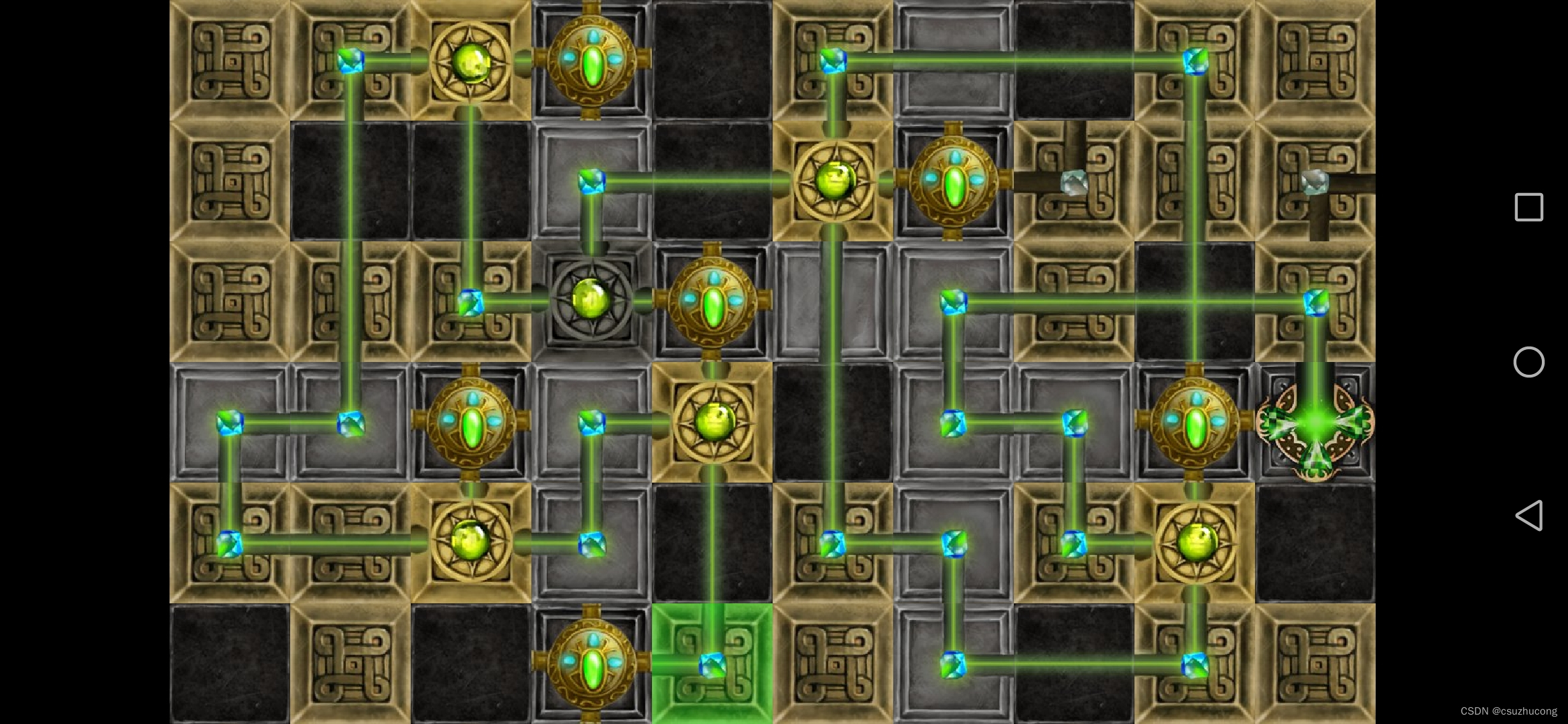
3-18

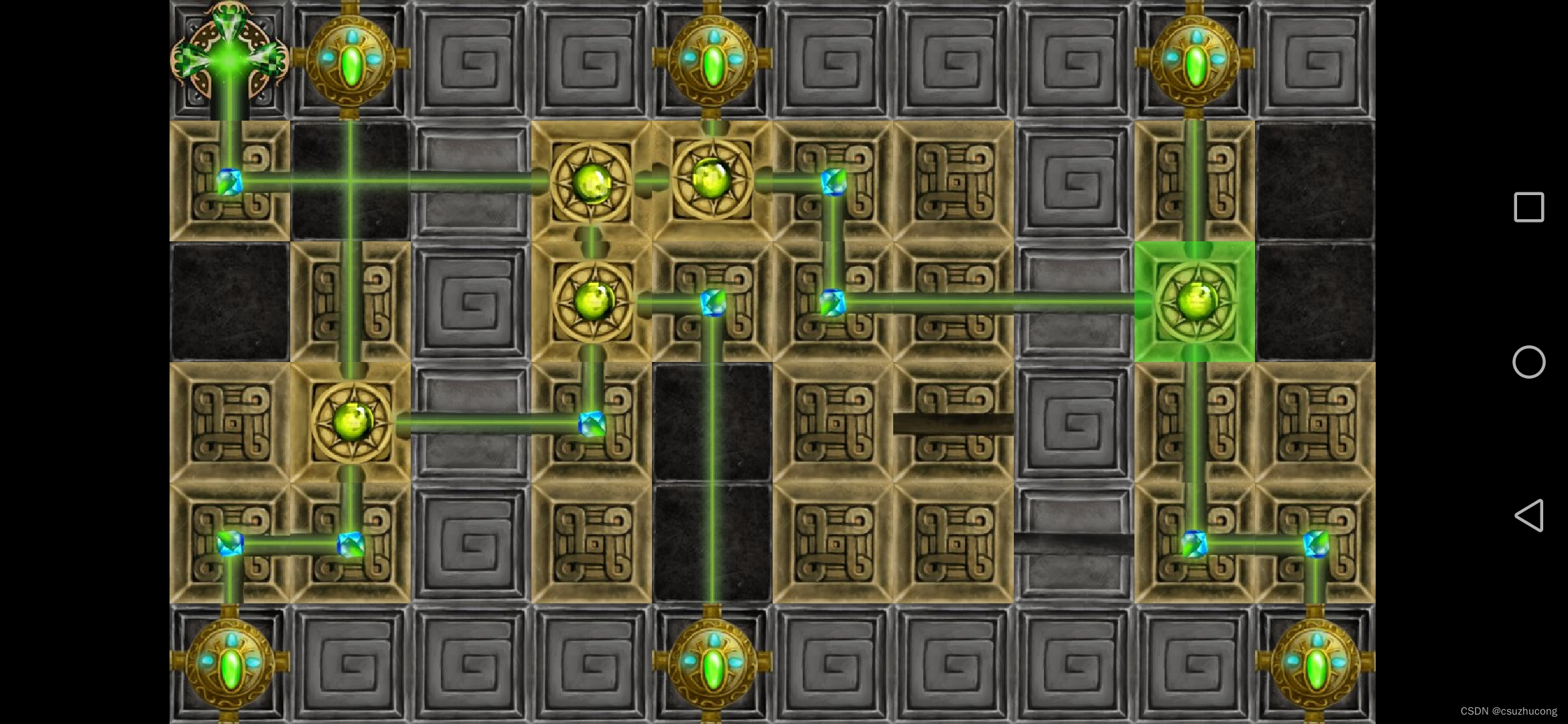
3-19

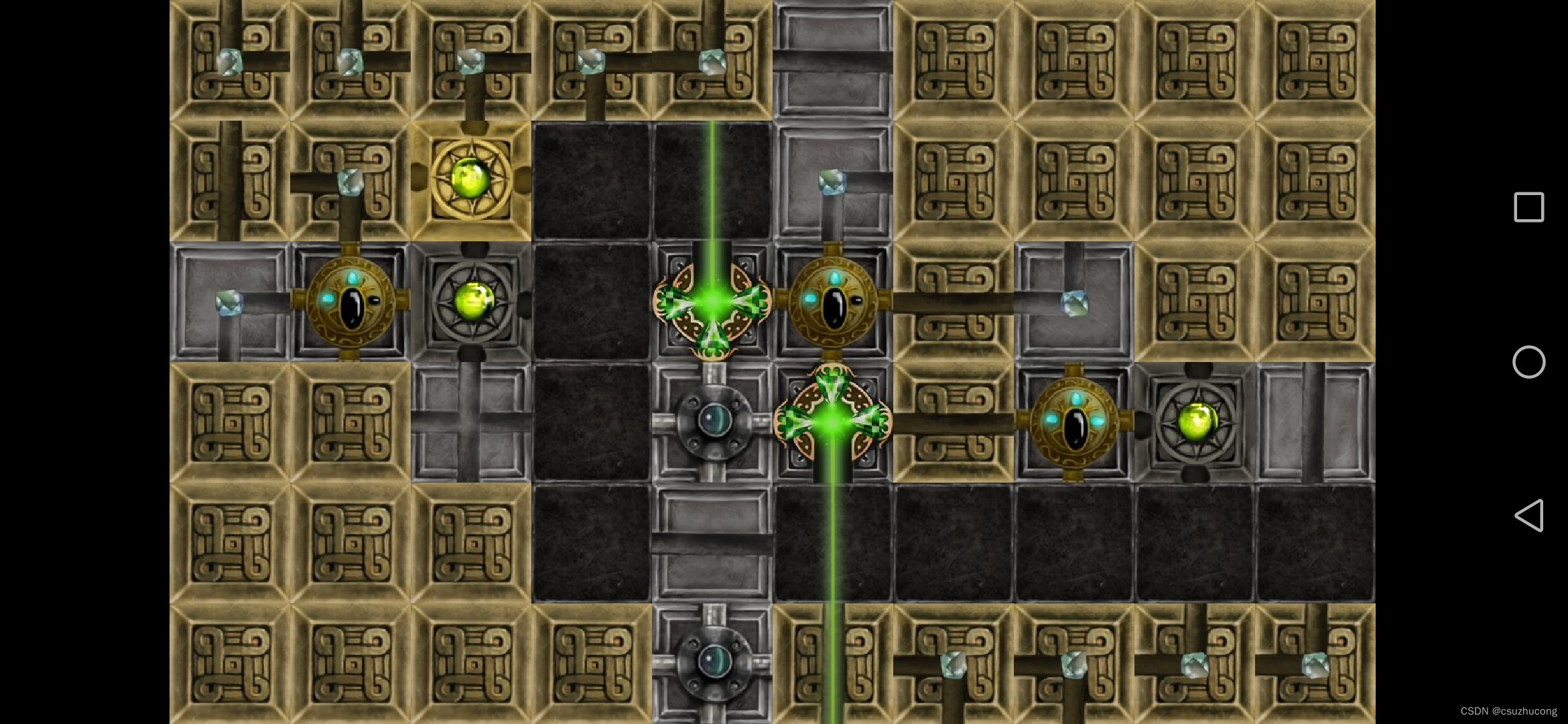
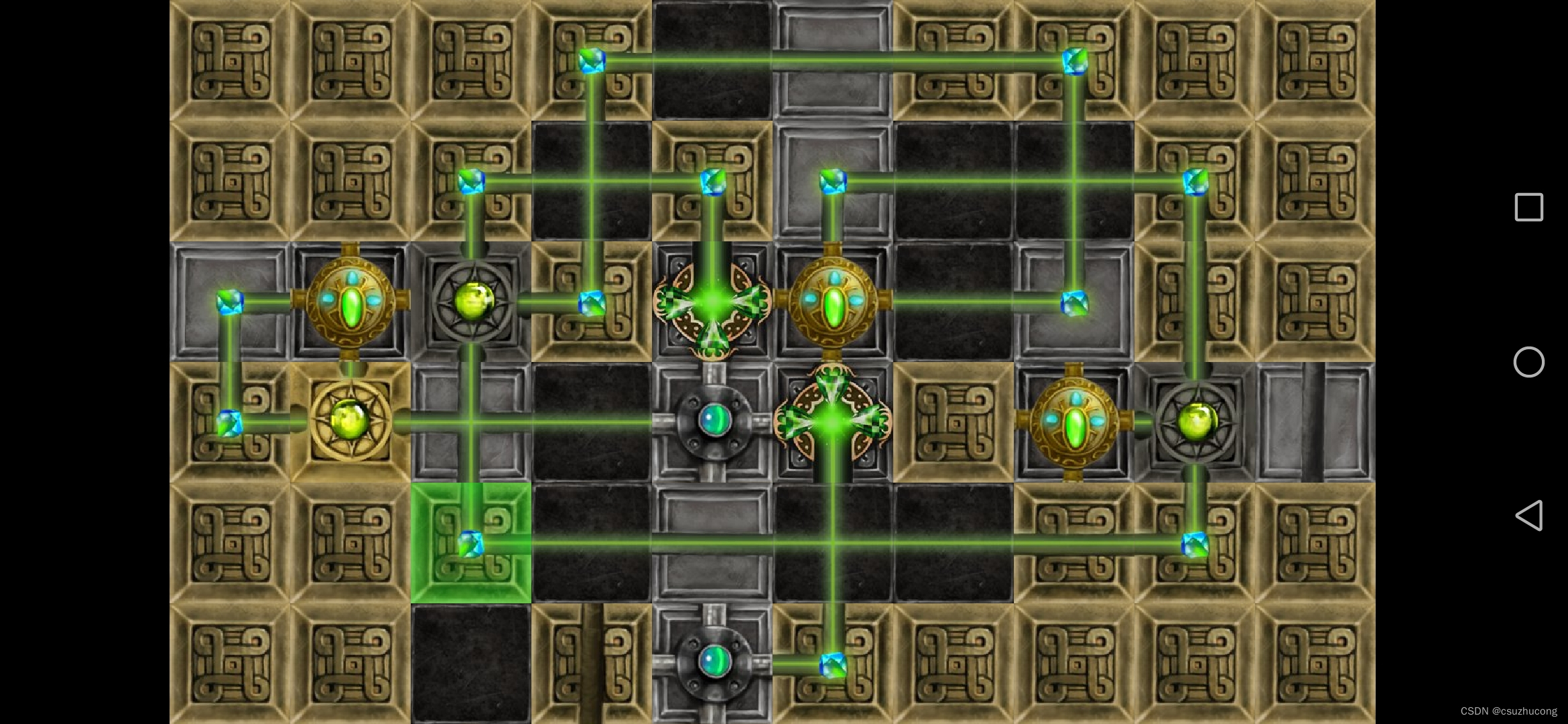
3-20

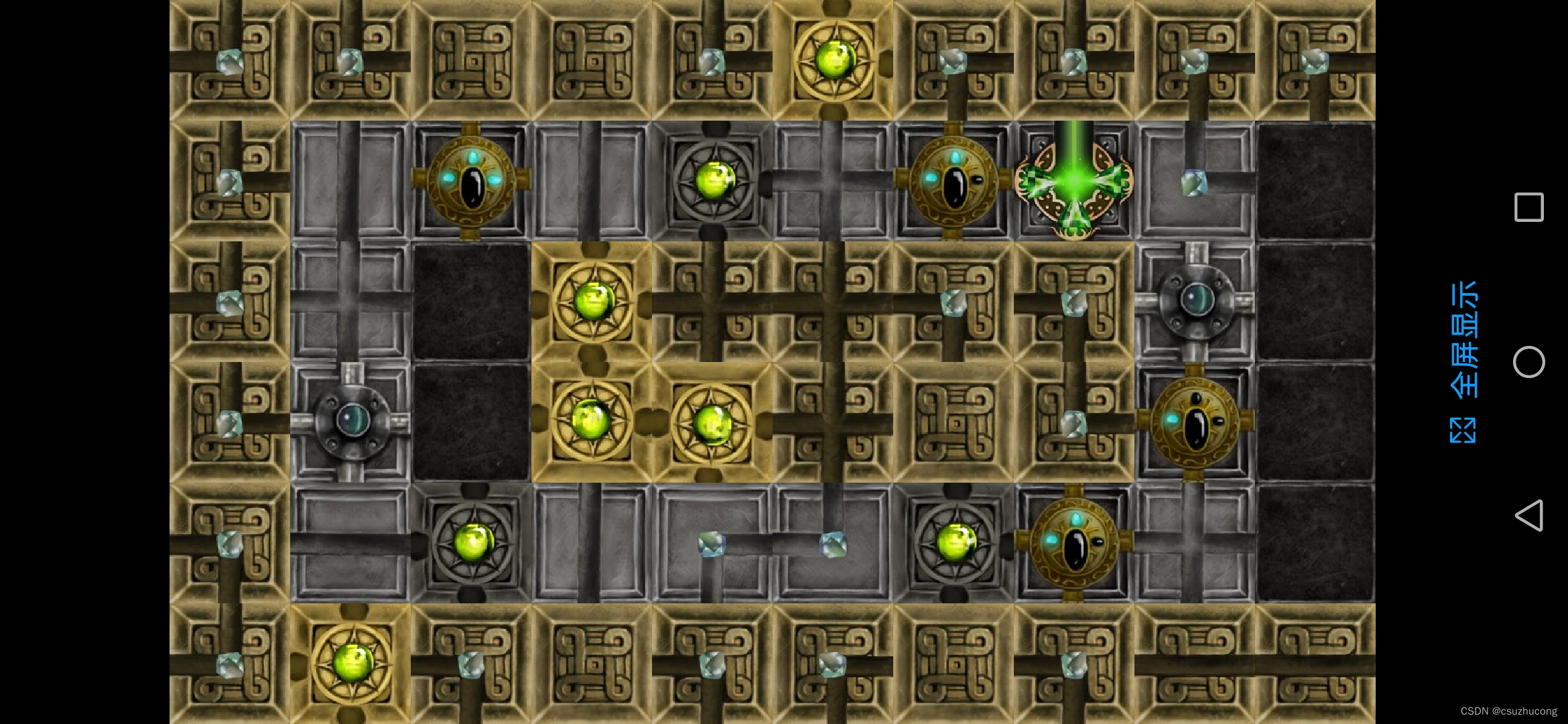
通关。