嵌入式学习day21

day20练习：

链式队列：

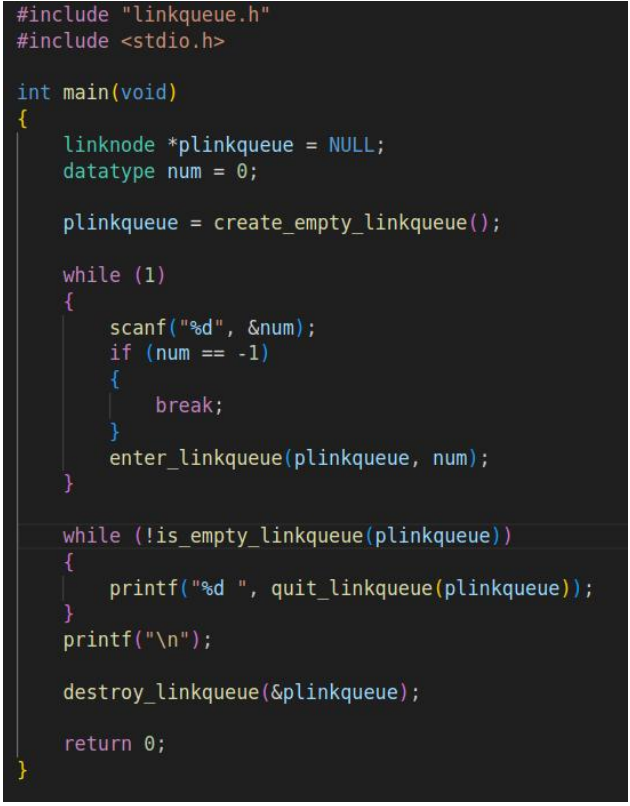
链式栈：

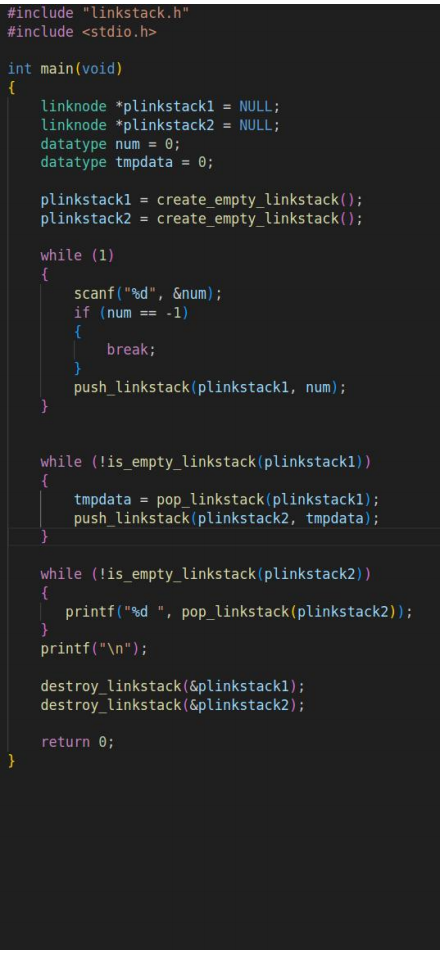
二叉树

1.概念：

        1.线性结构：描述数据一对一的关系（表）

        2.非线性结构：描述数据一对多（树）、多对多（图）的关系

2.树形结构：

        1.节点：组成树形结构的一个小的单元称为节点

                根节点：只有后继，没有前驱

                分支节点：既有前驱，又有后继

                叶子节点：只有前驱，没有后继

        2.前驱（祖先）：由哪个节点可以访问到该节点

        3.后继（子孙）：该节点可以后续访问到哪些节点

        4.层：根节点层数为1，后续每引申出的一个节点就在该节点层数上+1

        5.树的层数：树的层数由层数最高的节点对应的层数表示树的层数

        6.高度：节点高度是由该节点到最远的叶子节点的距离表示该节点的高度

        7.深度：节点深度是由该节点到根节点的距3，离表示节点深度

        8.树的高度 == 树的深度 == 树的层数

        9.度：后继节点的个数

3.二叉树：

        1.树形结构中的所有节点度数最大为2，称为二叉树

        2.二叉树节点类型：

                叶子节点（度数为0）

                只有左孩子

                只有右孩子

                左右孩子都有

        3.满二叉树和完全二叉树

                1.满二叉树：

                        所有的叶子结点均在同一层，且每层节点个数均为最大值

                        特性：

                                满二叉树第k层节点有2^(k-1)

                                满二叉树前k层节点有(2^k)-1

                2.完全二叉树：

                        二叉树的编号（如果节点编号为n，左孩子编号为2n，右孩子编号为2n+1）展开后

                        是连续的，称为完全二叉树

                3.完全二叉树的遍历形式：；

                        深度优先遍历（DFS）

                                前序遍历（先序遍历）：根左右

                                中序遍历：左根右

                                后序遍历：左右根

                        广度优先遍历（BFS）

                                层序遍历：逐层从左到右依次遍历

                4.完全二叉树的操作

                        1.节点定义

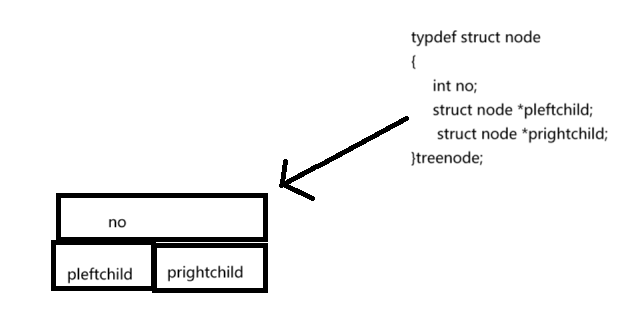
                        2.创建完全二叉树

                                通过函数递归完成完全二叉树的创建

                                申请节点空间

                                存放数据编号

                                如果存在左子树递归创建左子树

                                如果存在右子树递归创建右子树

                                                  

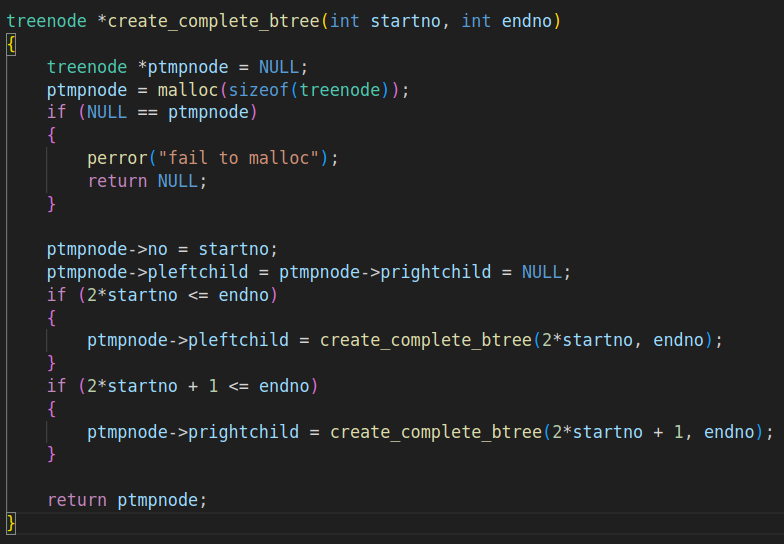
                        3.前序遍历

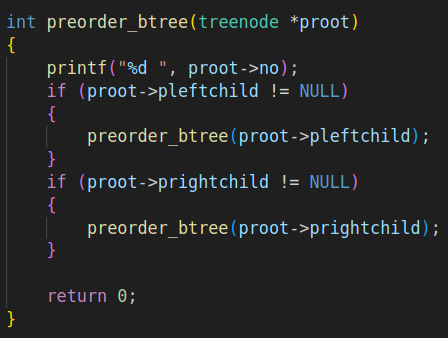
                        4.中序遍历

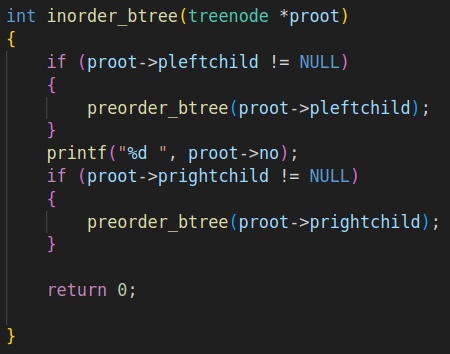
                        5.后序遍历

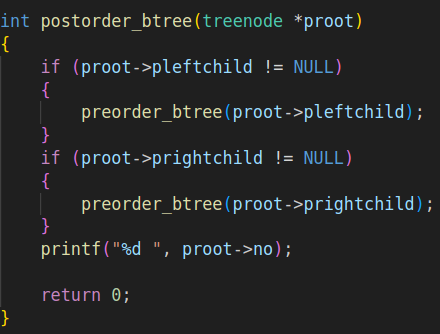
                        6.销毁

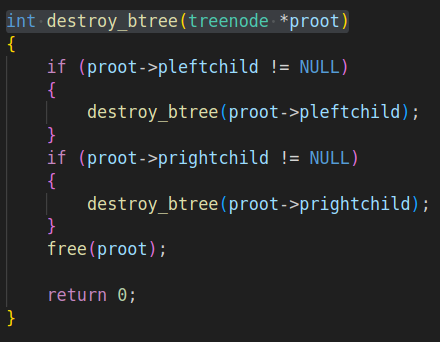
层序遍历

创建非完全二叉树

        非完全二叉树，每个结构都不一定相同

获得树的高度、深度、层数

二叉树的深度优先遍历（非递归实现）：

        前序遍历

        中序遍历

        后序遍历