线性回归建模
训练,预测
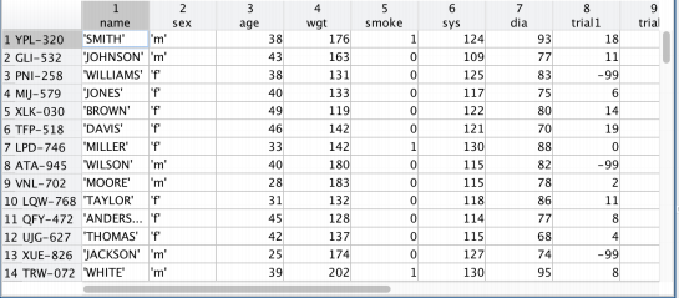
- { ( x ( i ) , y ( i ) ) } \{(x^{(i)},y^{(i)})\} {(x(i),y(i))} ⼀个训练样本, { ( x ( i ) , y ( i ) ) ; i = 1 , ⋯ , N } \{(x^{(i)},y^{(i)});i=1,\cdots ,N\} {(x(i),y(i));i=1,⋯,N} 训练样本集
- { ( x 1 ( i ) , x 2 ( i ) , y ( i ) ) } ⟶ { ( x ( i ) , y ( i ) ) } , x ( i ) = [ x 1 ( i ) x 2 ( i ) ] \{(x_1^{(i)},x_2^{(i)},y^{(i)})\}\longrightarrow\{(\mathbf{x}^{(i)},y^{(i)})\},\mathbf{x}^{(i)}=[\begin{array}{c}x_1^{(i)}\\x_2^{(i)}\end{array}] {(x1(i),x2(i),y(i))}⟶{(x(i),y(i))},x(i)=[x1(i)x2(i)]
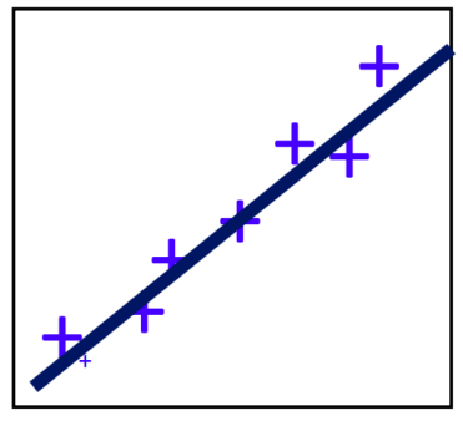
- 试图学习
- 一维: f ( x ) = w x + b f(x)=wx+b f(x)=wx+b 使得 f ( x ( i ) ) ≈ y ( i ) f(x^{(i)}) \approx y^{(i)} f(x(i))≈y(i)
- 多维: f ( x ) = w T x + b f(x)=\mathbf{w}^T \mathbf{x}+b f(x)=wTx+b 使得 f ( x ( i ) ) ≈ y ( i ) f(\mathbf{x}^{(i)}) \approx y^{(i)} f(x(i))≈y(i)
核心问题在于如何学习?
⽆约束优化梯度分析法
无约束优化问题
-
⾃变量为标量的函数 f f f: R → R \mathbf{R} \rightarrow \mathbf{R} R→R
min f ( x ) x ∈ R \min f(x) \quad x \in \mathbf{R} minf(x)x∈R -
⾃变量为标量的函数 f f f: R n → R \mathbf{R}^n \rightarrow \mathbf{R} Rn→R
min f ( x ) x ∈ R n \min f(x) \quad \mathbf{x} \in \mathbf{R}^n minf(x)x∈Rn -
Contour(等高图)
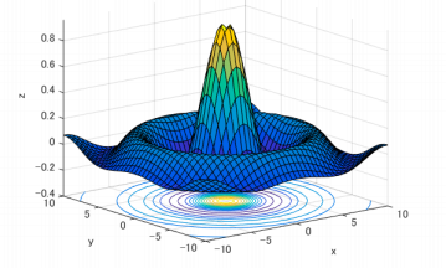
优化问题可能的极值点情况
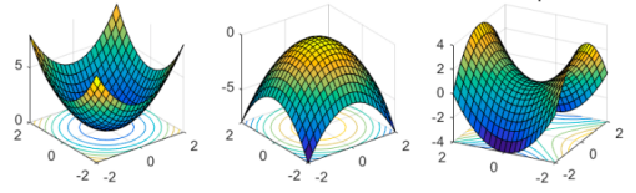
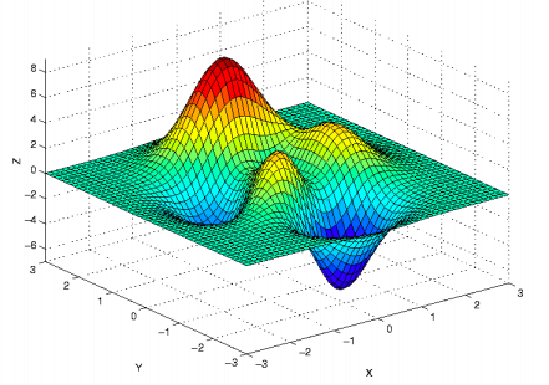
梯度和 Hessian 矩阵
-
一阶导数和梯度(gradient vector)
f ′ ( x ) ; g ( x ) = ∇ f ( x ) = ∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 ⋮ ∂ f ( x ) ∂ x n ] f'(x);\mathbf{g}\left(\mathbf{x}\right)=\nabla f(\mathbf{x})=\frac{\partial f(\mathbf{x})}{\partial\mathbf{x}}=\left[\begin{array}{c}\frac{\partial f(\mathbf{x})}{\partial x_1}\\\vdots\\\frac{\partial f(\mathbf{x})}{\partial x_n}\end{array}\right] f′(x);g(x)=∇f(x)=∂x∂f(x)= ∂x1∂f(x)⋮∂xn∂f(x) -
⼆阶导数和 Hessian 矩阵
f ′ ′ ( x ) ; H ( x ) = ∇ 2 f ( x ) = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x 1 ∂ x n ⋯ ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 ⋱ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 ∂ 2 f ( x ) ∂ x n 2 ] = ∇ ( ∇ f ( x ) ) T f''(x);\left.\mathbf{H}\left(\mathbf{x}\right)=\nabla^{2}f\left(\mathbf{x}\right)=\left[\begin{array}{ccccc}\frac{\partial^{2}f(\mathbf{x})}{\partial x_{1}^{2}}&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{1}\partial x_{2}}&\cdots&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{1}\partial x_{n}}\cdots\\\frac{\partial^{2}f(\mathbf{x})}{\partial x_{2}\partial x_{1}}&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{2}^{2}}\\&&\ddots\\\frac{\partial^{2}f(\mathbf{x})}{\partial x_{n}\partial x_{1}}&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{n}\partial x_{2}}&&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{n}^{2}}\end{array}\right.\right]=\nabla\left(\nabla f(\mathbf{x})\right)^{T} f′′(x);H(x)=∇2f(x)= ∂x12∂2f(x)∂x2∂x1∂2f(x)∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)∂xn∂x2∂2f(x)⋯⋱∂x1∂xn∂2f(x)⋯∂xn2∂2f(x) =∇(∇f(x))T
二次型
给定矩阵 A ∈ R n × n A \in \mathbf{R}^{n\times n} A∈Rn×n,函数
x T A x = ∑ i = 1 n x i ( A x ) i = ∑ i = 1 n x i ( ∑ j = 1 n a i j x j ) = ∑ i = 1 n ∑ j = 1 n x i x j a i j \mathbf{x}^{T}\mathbf{A}\mathbf{x}=\sum_{i=1}^{n}x_{i}\left(\mathbf{A}\mathbf{x}\right)_{i}=\sum_{i=1}^{n}x_{i}\left(\sum_{j=1}^{n}a_{ij}x_{j}\right)=\sum_{i=1}^{n}\sum_{j=1}^{n}x_{i}x_{j}a_{ij} xTAx=i=1∑nxi(Ax)i=i=1∑nxi(j=1∑naijxj)=i=1∑nj=1∑nxixjaij
被称为⼆次型。
例:对于 f ( x ) = x 1 2 + x 2 2 + x 3 2 f\left(\mathbf{x}\right)=x_1^2+x_2^2+x_3^2 f(x)=x12+x22+x32 ,可以写成下面的二次型:
f ( x 1 , x 2 , x 3 ) = [ x 1 , x 2 , x 3 ] [ 1 0 0 0 1 0 0 0 1 ] [ x 1 x 2 x 3 ] \begin{aligned} f(x_1,x_2,x_3)=\begin{bmatrix}x_1,x_2,x_3\end{bmatrix}\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} \end{aligned} f(x1,





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








