o1模型浅析

原创已于 2024-12-29 19:33:41 修改 · 1.1k 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #LLM

于 2024-12-29 17:22:04 首次发布

人工智能同时被 2 个专栏收录

7 篇文章

订阅专栏

LLM

2 篇文章

订阅专栏

o1模型

o1是什么

OpenAI发布新模型o1系列，可以实现复杂推理，旨在花更多时间思考，然后再做出响应。这些模型可以推理复杂的任务并解决比以前的科学、编码和数学模型更难的问题。

o1模型是没有开源的，而且没有相关论文，但是我们可以通过其他资料来了解这一个模型。

大模型智能的本质

快思考——聪明

回答一些通用的问题，相关的模型有gpt4 、通义、Llama等，速度与难度无关

慢思考——智慧

通过拆解、反思、推理、验证，来解决复杂的问题，推理速度与难度相关

因此可以说：

o1和gpt4：代表两条不同的技术路线，并没有谁替代谁一说
4o：GPT4+多模态，提升感知能力，本质上还是 gpt4 这一套

o1提升模型能力的方法

一个比较直接的想法是：把算力花在它的pretain阶段，给模型注入更多数理逻辑的预训练知识。

但是，当我们研读openai o1的技术报告时，我们会发现，它把这个算力更多地用在了2个地方：

用在了 rlhf 的训练上(post training)
用在了模型的推理阶段上(Test/Inferece)

优化推理输入

思维链的问题

之前，大模型解决复杂问题的能力：思维链（COT），一步一步引导

思维链的特点

**迭代式问题解决：**模型首先定义函数，然后逐步探索相关表达式，将复杂方程分解为更简单的组成部分，反映了一种结构化和有条理的方法。
**关键思维指标：**使用"Therefore"表示结论，"Alternatively"探索不同路径，"Wait"表示反思，以及"Let me compute"过渡到计算，突出了模型的推理阶段。
**递归和反思方法：**模型经常重新评估和验证中间结果，使用递归结构确保一致性，这在严谨的数学推理中很典型。
**假设探索：**模型测试不同的假设，随着获得更多信息而调整其方法，展示了推理过程中的灵活性。
**结论和验证：**最后，模型解方程并验证结果，强调在完成之前验证结论的重要性。

这种大段提示词在应用上的矛盾点：用答案解决答案（如果写这么多提示词说明本来就会这道题了，如果不会就写不出提示词）

思维链的难点

需要人工写
思考中间过程错误，全都错

解决方法

大模型生成思维链
中间过程校正

打分模型

模型不断生成各个步骤，然后用一个相对较小的模型进行打分，如果打分过低，就重新生成

为了训练 PRM，我们需要一份为每个步骤分类（正确或错误）的标签数据。与 ORM 相比，PRM 可以提供更详细和可靠的反馈。但是 PRM 对数据要求极高，需要为每个步骤构建标签，非常耗时耗力。

北京大学开源的数据集 Math-Shepherd，包含了 400k 个步骤级别的正确性标签

label中每一个 step 后面：+ 表示正确；- 表示错误（本质是一个二分类）

{
"input": "For how many digits $C$ is the positive three-digit number $1C3$ a multiple of 3? Step 1: To be a multiple of 3, the sum of the digits of a number must be divisible by 3. \u043a\u0438\nStep 2: The sum of the digits of $1C3$ is $1 + C + 3 = 4 + C$. \u043a\u0438\nStep 3: So I need to find how many values of $C$ make $4 + C$ a multiple of 3. \u043a\u0438\nStep 4: One way to do this is to list all the multiples of 3 that are between 4 and 7, inclusive, and see which ones have a digit C that makes them match. \u043a\u0438\nStep 5: The multiples of 3 that are between 4 and 7 are 4, 7, 10, 13, 16, 19, and 22. \u043a\u0438\nStep 6: I can eliminate 4 and 7, since they have different digits. \u043a\u0438\nStep 7: For 10, 13, and 16, the only digit that works is 1, since 3 does not match. \u043a\u0438\nStep 8: For 19, the only digit that works is 9, since 0, 1, 2, and 7 do not match. \u043a\u0438\nStep 9: For 22, the only digit that works is 2, since 0, 1, 7, and 9 do not match. \u043a\u0438\nStep 10: So the only possible values of C that make $1C3$ a multiple of 3 are 1, 9, and 2. \u043a\u0438\nStep 11: These are the only digits that make $1C3$ a multiple of 3, since any other digit would make the sum not divisible by 3. \u043a\u0438\nStep 12: Therefore, the answer is 3. The answer is: 3 \u043a\u0438", 

"label": "For how many digits $C$ is the positive three-digit number $1C3$ a multiple of 3? Step 1: To be a multiple of 3, the sum of the digits of a number must be divisible by 3. +\nStep 2: The sum of the digits of $1C3$ is $1 + C + 3 = 4 + C$. +\nStep 3: So I need to find how many values of $C$ make $4 + C$ a multiple of 3. +\nStep 4: One way to do this is to list all the multiples of 3 that are between 4 and 7, inclusive, and see which ones have a digit C that makes them match. +\nStep 5: The multiples of 3 that are between 4 and 7 are 4, 7, 10, 13, 16, 19, and 22. +\nStep 6: I can eliminate 4 and 7, since they have different digits. +\nStep 7: For 10, 13, and 16, the only digit that works is 1, since 3 does not match. +\nStep 8: For 19, the only digit that works is 9, since 0, 1, 2, and 7 do not match. +\nStep 9: For 22, the only digit that works is 2, since 0, 1, 7, and 9 do not match. +\nStep 10: So the only possible values of C that make $1C3$ a multiple of 3 are 1, 9, and 2. +\nStep 11: These are the only digits that make $1C3$ a multiple of 3, since any other digit would make the sum not divisible by 3. +\nStep 12: Therefore, the answer is 3. The answer is: 3 +", 
"task": "MATH"
}

{
"input": "Janet pays $40/hour for 3 hours per week of clarinet lessons and $28/hour for 5 hours a week of piano lessons. How much more does she spend on piano lessons than clarinet lessons in a year? Step 1: Janet spends 3 hours + 5 hours = <<3+5=8>>8 hours per week on music lessons. \u043a\u0438\nStep 2: She spends 40 * 3 = <<40*3=120>>120 on clarinet lessons per week. \u043a\u0438\nStep 3: She spends 28 * 5 = <<28*5=140>>140 on piano lessons per week. \u043a\u0438\nStep 4: Janet spends 120 + 140 = <<120+140=260>>260 on music lessons per week. \u043a\u0438\nStep 5: She spends 260 * 52 = <<260*52=13520>>13520 on music lessons in a year. The answer is: 13520 \u043a\u0438", 

"label": "Janet pays $40/hour for 3 hours per week of clarinet lessons and $28/hour for 5 hours a week of piano lessons. How much more does she spend on piano lessons than clarinet lessons in a year? Step 1: Janet spends 3 hours + 5 hours = <<3+5=8>>8 hours per week on music lessons. +\nStep 2: She spends 40 * 3 = <<40*3=120>>120 on clarinet lessons per week. +\nStep 3: She spends 28 * 5 = <<28*5=140>>140 on piano lessons per week. +\nStep 4: Janet spends 120 + 140 = <<120+140=260>>260 on music lessons per week. +\nStep 5: She spends 260 * 52 = <<260*52=13520>>13520 on music lessons in a year. The answer is: 13520 -", 

"task": "GSM8K“
}

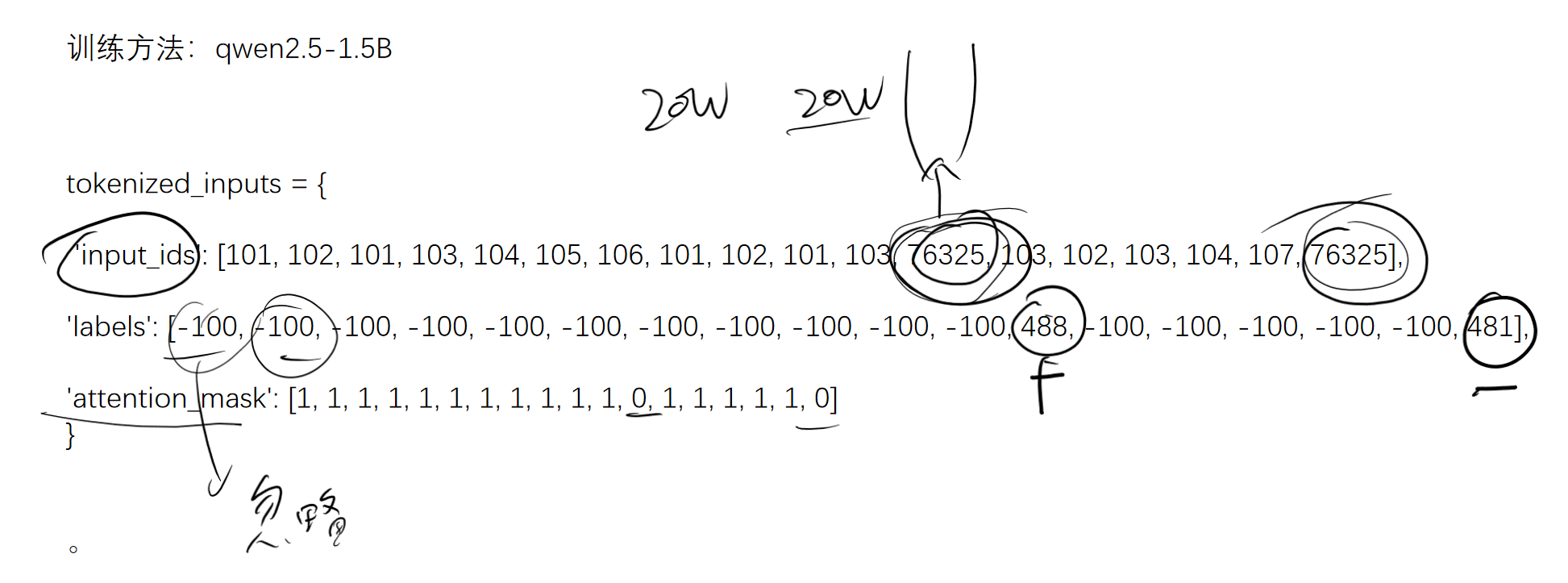
训练方式

对输入的特殊标识符位置进行预测（例如76325），预测结果表示正确（488，+）或者错误（481，-）

mask将特殊位置给掩盖住

推理方式

针对每一步进行打分

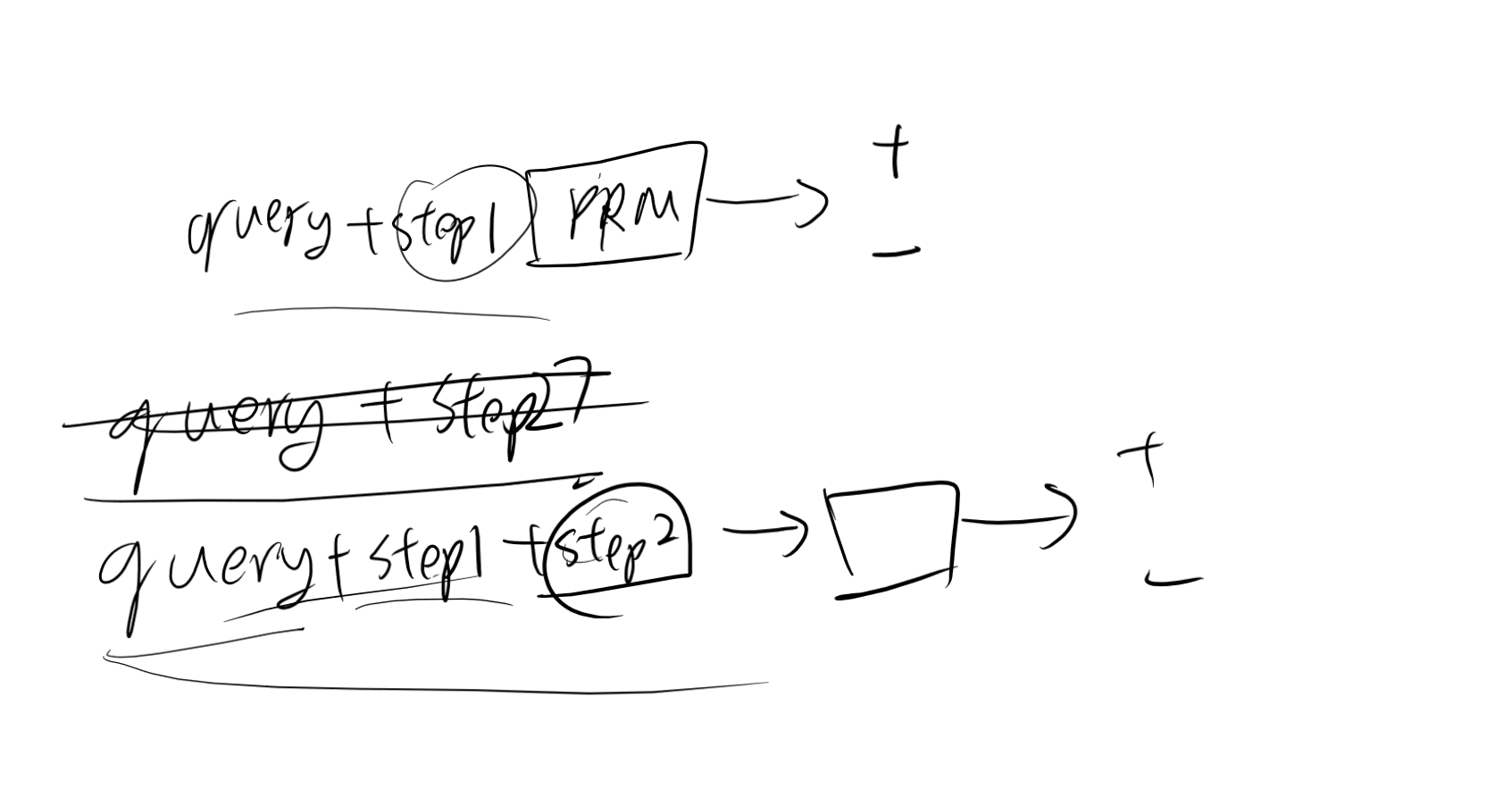
指导推理

相关模型

模型1：qwen2.5 14B 用于产生思维链和答案
模型2：PRM模型，基于qwen2.5 1.5B进行训练

搜索方式

Best-of-N：粗粒度，整体计算完成后，选出最优
Beam Search：细粒度，每一步选出 top K 个最优进行比较
Lookahead Search：每一步都保留所有情况，向前走若干步，选出分数较高的step然后保留

打分方式

连乘式（prod）：PRM会对每个step进行打分（离散标签下，这个得分表示概率）。我们将所有steps的得分相乘，用于表示整体的分数
最小式（min）：取所有steps中最小的得分作为整体得分。这是因为从直觉上，steps有一步出错，整个逻辑链就很可能出问题。所以我们取最坏的情况作为整体得分。
最后一步式（last step）：当你训练PRM时，你肯定不是把单个step喂给PRM让它去做打分，而是把全部steps一起喂给它，让他们拥有上下文关系（PRM需要根据前面的steps去判断当前step的得分）。所以理论上，你取last step的得分，也可以反映出整体得分。

prod和min都是 openAl 在《let’s verify step by step》中探索过的方法，last step则是deepmind在本文中使用的方法。这些方法间没有绝对好坏之分，取决于你是如何设计整个训练过程的。我们在这里只强调“需要制定出一种规则，能够将PRM的单步打分映射成整体打分。”

如何选择搜索方式

搜索的效果（也即模型的推理效果）受到搜索预算和问题难度的限制，我们是在这些限制中去选择合适的搜索方法。
当搜索预算较小，问题较难时，更适合beam search方法，但要注意超参的调整
当搜索预算较大，问题较简单时，更适合best-of-N方法
当PRM训练得足够好时，更复杂的搜索方法（例如lookahead search）的表现可能并不好
当问题特别困难时，test-time scaling law的作用可能有限，这时可能有必要重新审视pretrain阶段，通过加/调整数据比例，扩张模型规模等等方式，给pretrain模型十注入更多的相关知识。

蒙特卡洛树搜索算法（MCTS）

多臂老虎机

假设有若干个黑盒，每个黑盒里面抽取后得分分别在 M1, M2, M3, M4… 附近晃动

现在只有 T 次抽取机会，如何使得总的分数最高？

很容易想到通过如下方式进行抽样，但是都有自己的缺陷：

纯随机（Random）：每次随机选一个摇臂进行摇动。（劣势：能算个期望收益，但收益不是最大的。）
仅探索（Exploration-only）：每个摇臂摇动T/K次。相当于每个摇臂摇动的次数都一样。（劣势：浪费次数在收益较差的摇臂上）
仅利用（Exploitation-only）：首先对每个摇臂摇动一次，记录收益。随后对剩余的 T-K 次机会全部摇收益最大的摇臂。（劣势：摇动一次记录的收益随机性太强，不可靠）

可以使用强化学习的方式进行抽样，边应用边学习

单轮优化

一开始均匀抽取，然后使用如下公式进行抽取：
$UCB_j=\bar{X}_j+C\sqrt{\frac{2lnN_C}{N_j}}$
其中： $\bar{X}_j$ 表示已经 $j$ 号样本已经抽样的平均分， $N_c$ 表示总访问次数， ${N_j}$ 表示第 $j$ 号样本样本访问的次数

基于以下两个因素进行考量：

平均得分（利用），平均得分体现了样本的总体水平
访问次数低的会有附加分（探索），访问较低时时对于平均分的计算可能不准

但是多臂老虎机有个要求：即时反馈

但是并不是所有场景都有即时反馈，例如对于下棋：只有当下完以后复盘才能知道当前步下得好不好

对于不能即时反馈的场景：

最后错的，不一定每步都错
最后对的，不一定每步都对

多轮优化

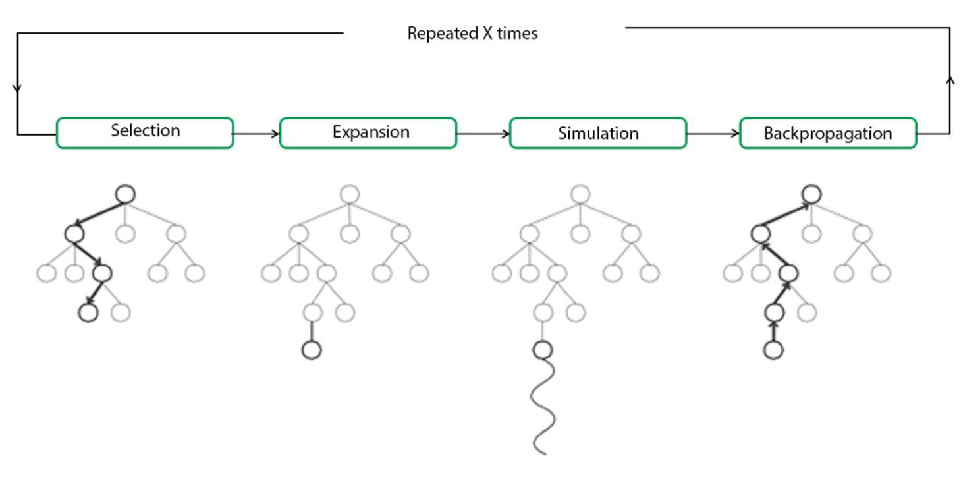
使用 蒙特卡罗树搜索（Monte Carlo Tree Search，MCTS）

优点：搜索空间无穷大，无法穷举

步骤：

选择（Selection）

从根节点R开始，递归地选择最优子节点（通过UCB，后续节点选择展开讲解），直到到达叶子节点L。
探索（Expansion）

如果L不是终止节点（即它没有结束游戏），则创建一或多个子节点并从中随机选择一个子节点C进行探索。
模拟/仿真（Simulation、Rollout）

从C运行一个模拟的rollout，直到获得一个结果。（后续节点模拟会举例子展开讲解如何模拟）
反传（Backpropagation）

用模拟结果（终止节点的代价或游戏的终局分数）更新当前的移动序列，更新模拟路径中节点的奖励均值和被访问次数。注意，反传的过程中，每个节点必须包含两个重要的信息：基于模拟结果的估计值和它被访问的次数。