统计方法学——EM算法及其推广

EM算法导入

EM算法是一种迭代算法，在概率统计中，如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法，或贝叶斯估计法估计模型参数，但是有些含有隐变量，就不能直接使用，因此EM就是解决这种问题的一种方法。
例子：

分析：


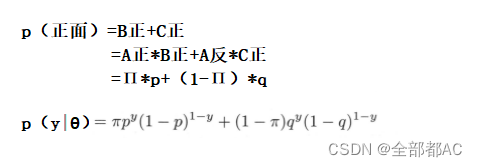
显然，y是观测变量，要么是1，要么是0，进一步重复实验

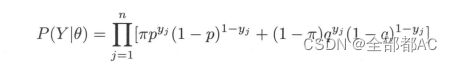
EM算法的实现过程

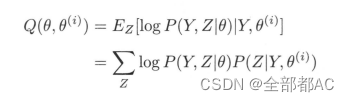
一般地，用Y表示观测随机变量的数据Z表示隐随机变量的数据。Y和Z连在一起称为完全数据，观测数据Y又称为不完全数据。假设给定观测数据Y,其概率分布是 P(YIθ) 其中θ是需要估计的模型参数，那么不完全数据Y的似然函数是 P(YIθ)， 对数似然函数 L(θ) = log(Y|θ）；假设Y和Z的联合概率分布是P(Y, ZIθ) ，那么完全数据的对数似然函数是 log P(Y, Z|θ)。
EM 算法通过迭代求 L(θ) = log P(YIθ) 的极大似然估计。每次选代包含两步，E步，求期望 ;M 步，求极大化。

EM算法的导出

算法的原理我们以及了解了，那么为什么可以通过这样的方式实现对极大似然的估计？


所以，EM 算法是通不断求解下界的极大化逼近求解对数似然函数极大化的算法。

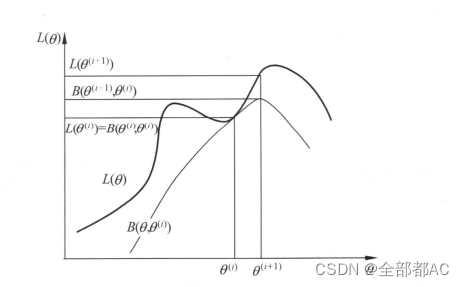
EM算法的收敛性

直观的理解就是，我们可以证明得到在经过一定的迭代之后，能够使得对数似然函数比上一次迭代的参数更大，那么我们就可以认为，经过足够过的迭代，可以使得参数最大化，此时的θ就可以认为是最大化的参数。