题目大意:
给你N个区间,你可以任意找到K个区间,对应加和这K的区间所重叠的部分。
求加和。
思路:
1、首先我们枚举K个区间去维护和的话,肯定是要超时的,正难则反,我们不妨考虑一个点的贡献度。
假设我们x这个点被覆盖了y次,那么很明显,有y个区间都包含x这个点,那么对应这个点可以进行的贡献度为:C(y,k);
2、观察到数据范围很大,直接这样求是不行的,无论是空间还是时间,都是一个巨大的数据量。然而N是并不大的,所以我们考虑离散化这N个区间的点。
然后对于区间的贡献度进行查询即可。
然而我们不能直接对离散化之后的两个点之间的部分进行查询,所以我们离散化一个区间是要变成四个点:
l,r,l+1,r+1.
3、那么对于每个区间的贡献度就是:C(整个区间被覆盖的次数,k)*(区间的长度);
过程维护一下即可。
map映射注意细节。
初始化组合数注意大小。
附赠一组数据:
4 1
1 10
2 9
15 20
16 21
ans=30.
Ac代码:
#include<stdio.h>
#include<string.h>
#include<map>
#include<algorithm>
using namespace std;
#define LL long long int
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
const LL mod = 1000000007;
const LL N = 500000+5;
const LL M = 5e5+3;
struct node
{
LL x,y;
}a[250000];
LL vis[3000000];
LL tree[3000000];
LL flag[3000000];
LL q[3000000];
LL b[5000000];
LL fac[3000005]; //阶乘
LL inv_of_fac[3000005]; //阶乘的逆元
LL qpow(LL x,LL n)
{
LL ret=1;
for(; n; n>>=1)
{
if(n&1) ret=ret*x%mod;
x=x*x%mod;
}
return ret;
}
void init()
{
fac[1]=1;
for(LL i=2; i<=M; i++)
fac[i]=fac[i-1]*i%mod;
inv_of_fac[M]=qpow(fac[M],mod-2);
for(LL i=M-1; i>=0; i--)
inv_of_fac[i]=inv_of_fac[i+1]*(i+1)%mod;
}
LL C(LL a,LL b)
{
if(b>a) return 0;
if(b==0) return 1;
return fac[a]*inv_of_fac[b]%mod*inv_of_fac[a-b]%mod;
}
void pushdown(LL l,LL r,LL rt)//向下维护树内数据
{
if(flag[rt])//如果贪婪标记不是0(说明需要向下进行覆盖区间(或点)的值)
{
LL m=(l+r)/2;
flag[rt*2]+=flag[rt];
flag[rt*2+1]+=flag[rt];
tree[rt*2]+=(m-l+1)*flag[rt];//千万理解如何覆盖的区间值(对应线段树的图片理解(m-l)+1)是什么意识.
tree[rt*2+1]+=(r-(m+1)+1)*flag[rt];
flag[rt]=0;
}
}
void pushup(LL rt)
{
tree[rt]=tree[rt<<1]+tree[rt<<1|1];
}
void build( LL l ,LL r , LL rt )
{
if( l == r )
{
tree[rt]=0;
flag[rt]=0;
return ;
}
else
{
LL m = (l+r)>>1 ;
build(lson) ;
build(rson) ;
pushup(rt) ;
}
}
void update(LL L,LL R,LL c,LL l,LL r,LL rt)
{
if(L<=l&&r<=R)//覆盖的是区间~
{
tree[rt]+=c*((r-l)+1);//覆盖当前点的值
flag[rt]+=c;//同时懒惰标记~!
return ;
}
else
{
pushdown(l,r,rt);
LL m=(l+r)/2;
if(L<=m)
{
update(L,R,c,lson);
}
if(m<R)
{
update(L,R,c,rson);
}
pushup(rt);
}
}
LL Query(LL L,LL R,LL l,LL r,LL rt)
{
if(L<=l&&r<=R)
{
return tree[rt];
}
pushdown(l,r,rt);
LL m=(l+r)>>1;
LL ans=0;
if(L<=m)
{
ans+=Query(L,R,lson);
}
if(m<R)
{
ans+=Query(L,R,rson);
}
return ans;
}
int main()
{
init();
LL n,k;
while(~scanf("%I64d%I64d",&n,&k))
{
LL cnt=0;
map<LL ,LL >s;
map<LL ,LL >rs;
memset(vis,0,sizeof(vis));
memset(tree,0,sizeof(tree));
memset(flag,0,sizeof(flag));
for(LL i=0;i<n;i++)
{
scanf("%I64d%I64d",&a[i].x,&a[i].y);
b[cnt++]=a[i].x;b[cnt++]=a[i].y;
b[cnt++]=a[i].x+1;b[cnt++]=a[i].y+1;
}
LL tot=0;sort(b,b+cnt);
for(LL i=0;i<cnt;i++)
{
if(s[b[i]]==0)
{
s[b[i]]=++tot;
rs[tot]=b[i];
}
}
LL qq=0;
build(1,tot,1);
for(LL i=0;i<n;i++)
{
update(s[a[i].x],s[a[i].y],1,1,tot,1);
vis[s[a[i].x]]=1;
vis[s[a[i].y]]=1;
}
LL output=0;
for(LL i=1;i<=tot;i++)
{
output+=C(Query(i,i,1,tot,1),k);
output%=mod;
if(rs[i]+1==rs[i+1])continue;
else
{
output+=C(Query(i,i,1,tot,1),k)*(rs[i+1]-rs[i]-1);
output%=mod;
}
}
printf("%I64d\n",output);
}
}
/*
4 1
1 10
2 9
15 20
16 21
*/








 本文介绍了一个经典的区间覆盖问题,通过离散化和线段树的数据结构优化算法,解决了大规模数据下寻找K个区间交集内整数点总数的问题。
本文介绍了一个经典的区间覆盖问题,通过离散化和线段树的数据结构优化算法,解决了大规模数据下寻找K个区间交集内整数点总数的问题。
 ). You are given two integers
). You are given two integers
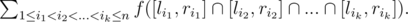
 ;
; ;
; .
.















 668
668

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








