CF 361 E. Mike and Geometry Problem 排列组合

E. Mike and Geometry Problem

time limit per test

 3 seconds

memory limit per test

 256 megabytes

input

 standard input

output

 standard output

Mike wants to prepare for IMO but he doesn't know geometry, so his teacher gave him an interesting geometry problem. Let's define f([l, r]) = r - l + 1 to be the number of integer points in the segment [l, r] with l ≤ r (say that 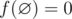). You are given two integers n and k and nclosed intervals [li, ri] on OX axis and you have to find:

In other words, you should find the sum of the number of integer points in the intersection of any kof the segments.

As the answer may be very large, output it modulo 1000000007 (109 + 7).

Mike can't solve this problem so he needs your help. You will help him, won't you?

Input

The first line contains two integers n and k (1 ≤ k ≤ n ≤ 200 000) — the number of segments and the number of segments in intersection groups respectively.

Then n lines follow, the i-th line contains two integers li, ri ( - 109 ≤ li ≤ ri ≤ 109), describing i-th segment bounds.

Output

Print one integer number — the answer to Mike's problem modulo 1000000007 (109 + 7) in the only line.

Examples

input

3 2
1 2
1 3
2 3

output

5

input

3 3
1 3
1 3
1 3

output

3

input

3 1
1 2
2 3
3 4

output

6

Note

In the first example:

;

;

.

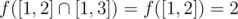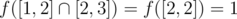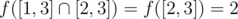So the answer is 2 + 1 + 2 = 5.

 

 

题目求线段点重合大于K次的组合次数，求和即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>

using namespace std;

int n,k;

struct node
{
    long long x;
    int f;


}pt[500005];

long long fac[200005];
long long powdd[200005];

bool cmp(node a,node b)
{
    return a.x<b.x;
}

long long mod=1e9+7;

long long powd(long long a,long long b)
{
    long long ans=1;
    while(b>0)
    {
        if(b%2==1)
        {
           ans=ans*a%mod;
        }
        a=a*a%mod;
        b/=2;
    }

    return ans;
}

long long C(long long b,long long a)
{
    long long ans=1;
    if(a>b)
        return 0;

    ans=(fac[b]*powdd[a]%mod)*powdd[b-a]%mod;
    return ans;
}

int main()
{
    fac[0]=1;
    for(long long i=1;i<=200000;i++)
        fac[i]=fac[i-1]*i%mod;
    for(int i=0;i<=200000;i++)
        powdd[i]=powd(fac[i],mod-2)%mod;

    while(~scanf("%d%d",&n,&k))
    {
        for(int i=0;i<n;i++)
        {
            scanf("%lld%lld",&pt[i*2].x,&pt[i*2+1].x);
            pt[i*2].f=1;pt[2*i+1].f=-1;
            pt[i*2+1].x++;
        }

        sort(pt,pt+(2*n),cmp);
        int ct=0;
        int pre=-(1e9+7);

        long long ans=0;
        for(int i=0;i<2*n;i++)
        {
            if(i!=0)
            {
                if(pt[i].x!=pt[i-1].x)
                {
                    //printf("%lld:%d  ct:%d plus:%lld\n",pt[i].x,pre,ct,(C(ct,k)*(pt[i].x-pre)%mod)%mod);
                    ans=(ans+C(ct,k)*(pt[i].x-pre)%mod)%mod;
                }
            }

            ct+=pt[i].f;
            pre=pt[i].x;
        }

        printf("%lld\n",ans);
    }


}