电动汽车充电站优化配置

面向需求的电动汽车快速充电基础设施配置

摘要

智慧城市的概念致力于采用更环保的技术来减少碳排放，以缓解全球变暖。在此背景下，交通领域正经历范式转变，向电动汽车（EV）的转型在减少碳排放方面具有巨大潜力。然而，预期的电动汽车渗透率受到若干挑战的制约，其中包括续航里程较短、充电速率较慢以及充电地点普遍缺乏，这些因素共同导致了电动汽车驾驶者的续航焦虑。与此同时，预计大量增加的电动汽车负荷可能降低配电网络的电压稳定性。为减轻续航焦虑，我们提出一种两阶段解决方案，用于配置和规划直流快速充电站（CS）网络，以满足预期的能源需求，在确保一定用户体验质量（例如可接受的等待时间和更短的充电行驶距离）的同时最小化部署成本。该方案通过考虑配电网容量、确定支持电动汽车充电峰值需求的变压器额定容量，并根据对配电网络的影响添加最少数量的电压调节器，从而维持电压稳定性。我们提出、评估并比较了两种充电站网络扩展模型，以确定一种成本效益高且自适应的充电站配置方案，能够高效扩展充电站网络以满足未来电动汽车充电及传统负荷需求。我们还提出了两种启发式方法，并将我们的方案与之进行比较。最后，开发了一个定制的基于Python的离散事件模拟器来验证我们的研究成果。

索引术语

电动汽车，充电站，电压稳定性，排队论

符号说明

最便宜位置优先选择 CheapestLocationSelect FirstCSDP-WA CSDP 工作负载分配 CSDP 充电站容量规划与选址 CS 充电站 EV 电动汽车 ILP 整数线性规划 LLSF 最大位置优先选择

I. 引言

Recently，智慧城市的概念已经出现，并随着许多政府和市政当局提出现代化城市的愿景和期望而成为现实，推出了雄心勃勃的倡议以实现这一目标。这些愿景在公共和私营部门的贡献下，通过加速技术进步以实现预期目标[2][3]。未来城市的智慧城市愿景包含诸多理念，包括智能公用设施、智能健康服务、智能治理、智能产业和智能交通等[3]。

电动汽车（EV）被视为智慧城市的主要交通方式。为了加快电动汽车的普及，各国政府已宣布实施购买电动汽车的补贴计划。例如，魁北克政府宣布提供8000加元的电动汽车购置补贴，以推动电动汽车市场在2020年达到10万辆的目标。但在距离魁北克设定的最后期限仅剩两年时，该省道路上的电动汽车数量仅为2.4万辆[4]。另一方面，奥斯陆通过免除电动汽车购置税、提供免费停车和免收通行费等措施，同时确保公共充电站数量充足[3]，已在城市中部署了超过2,000个充电站。由于这些举措的实施，奥斯陆已成为全球首个电动汽车大规模市场。2015年，奥斯陆新注册汽车中近30%为电动汽车[3]。

然而，在实践中，购买电动汽车的激励措施可能不足以促进电动汽车的普及。这些激励措施需要配备充足的充电设施，以减少电动汽车驾驶者的续航焦虑。由于电动汽车电池容量相对较小，需要频繁充电。这一需求加上相对缓慢的充电过程，necessitates在战略位置智能且充分地分布充电设施，以确保驾驶员能在舒适行驶距离内到达充电站，并在站内有可容忍的等待时间。由于部署充电站是一个昂贵的项目，因此充电站网络的战略性布局和容量规划应与未来几年不断增长的需求相匹配。

此外，在进行大规模部署之前，必须考虑大量电动汽车接入及其异步连接对电网造成的影响，这可能会在高峰期使电网不稳定。据报道，在葡萄牙，电动汽车接入电网的比例仅达到总量的10%时，在用电高峰时段充电就可能导致电压水平显著下降[5]。因此，充电站的有效部署必须维持配电网的电压稳定性。

考虑到这些显著特征在充电站供给模型中的重要性，刘等人优化了所需充电站的数量[6]，以最小化投资成本以及配电网中的功率损耗。在[6]中，根据电网容量选定了潜在位置（即不降低电压水平），因此为了维持电压稳定性，他们可能无法考虑一些在电动汽车用户便利性方面更合适的位置。为确保电动汽车用户的便利性，他们测量了服务半径，但未考虑充电站的预期等待时间。另一方面，[7]提出在环形高速公路沿线部署一组快速充电器，以最小化价格和等待时间，但未考虑电压稳定问题。由于部署充电站网络成本较高，该网络应能适应未来需求。然而，[6]和[7]均未考虑这一点。在[8]中，充电站网络在预定义预算内随需求逐步扩展，但他们未考虑任何电力约束和等待时间，且所提出的充电站选址决策仅基于当前需求（即在特定时间后，根据现有需求扩展充电站网络）。在当前规划问题中考虑未来需求，可使充电站网络在长期运行中更具竞争力和成本效益。下文小节将提供更详细的文献综述。

A. 文献综述

在[9]中提出了一种利润最大化模型，用于将停车场改造为太阳能充电站。最近的两项研究[10]和[11]也鼓励将停车站用作充电站。这类举措凸显了在公共场所提供充足充电设施的迫切需求，同时也揭示了与现有基础设施融合所面临的挑战。大量研究工作探讨了利用公共场所作为充电站以支持不断增长的电动汽车市场的可行性。

在[12]中分析了引入公共充电站的重要性，其中基于一个考虑充电成本的函数研究了购买电动汽车的意愿。不断增长的电动汽车普及率要求用充电站取代传统加油站[13]，但电动汽车充电模式与传统车辆加油存在显著差异，因此无法直接采用此类方案。因此，需要以不同的方式规划充电网络，尤其是在预期成本非常高且需确保服务质量（QoS）以鼓励人们转向电动汽车的情况下。Ucer等人[14]利用俄亥俄州哥伦布市的实际数据，分析了用户在直流快速充电站的使用体验。尽管该研究[14]未涉及充电站的位置问题，但它分析了规模（例如充电桩数量和电力容量）对城市、郊区和农村地区电动汽车排队延迟的影响。

为了减少续航焦虑，考虑现有道路网络和驾驶行为对充电站部署问题具有重要意义。在[15]中，提出了一种整数线性规划方法，以布置一定数量的充电站，覆盖道路网络中任意两个连续节点之间的路径。为实现相同目标，密歇根大学开展了大量工作[16]，其中他们考虑了密歇根州季节间充电行为的变化，并引入了一种元启发式算法来解决此问题。类似地，在[17]中针对波士顿和都柏林的道路网络，确定了最少数量的充电站，以确保每辆电动汽车都能到达一个可访问的充电站。

每辆电动汽车。陶等人[18]采用遗传算法选择一组充电站位置，以最小化电动汽车电池过度放电的时间。在[19]中，针对城市区域提出了一个充电站选址问题，旨在最小化安装成本，其中作者分析了此类问题的复杂性，并比较了不同的求解算法。为了最小化成本，[20]基于出行行为优化了充电站的合适位置。

可持续的充电设施还必须维护社会经济价值，从而实现能源稳定[21]。为了减轻电动汽车充电对电网的影响，依赖电池更换或车辆到电网（V2G）[22]，或结合由智能能源管理系统支持的社区微电网[23]以最小化充电成本，可能是一种辅助解决方案，特别是当电动汽车充电需求每天持续上升时。马诺什等人[24]分析了大规模电动汽车渗透对道路网络和电网的影响，而在[25]中通过半动态交通分配模型表示交通流量分布，以评估充电行为对电网的影响。考虑到电网与道路网络之间的相互依赖性，提出了一种电力系统与电气化交通网络的整体框架，作为“网络中的网络”来提升这些系统的运行性能，并通过耦合代理（例如电动汽车和充电站）[26]说明所需的信息交换。尽管这些研究（[24] - [26]）强调了电动汽车充电对电网造成的影响，但并未提出充电站的战略布局以最小化此类影响。为缓解此类影响，林等人[19]在研究中考虑了电网的总容量而非各节点间的容量变化，但未考虑充电站的等待时间。通过群优化方法，[27]寻找充电站的最优位置，作者假设电网容量可根据需要增加，而[28]则建议增加更多变压器。维持电压稳定性也在[9],[29]和[30]中被考虑，用于确定充电站的最优位置，但未考虑等待时间或舒适行驶距离。崔等人[31]提出了最小化城市区域安装成本的方法，同时考虑了为维持电能质量所需的保护装置成本。由于大规模集成快速充电器可能会显著降低电能质量[32]，因此在[33]中，作者提出依托替代能源（如可再生能源、V2G）进行快速充电器的战略布局，以减少谐波失真。然而，他们并未提出应对未来日益增长需求的解决方案，而电动汽车渗透率的增长趋势要求采取物理措施（如扩展电网、部署更多电压调节器）以及战略措施，以维持电压稳定性。

在进行战略性部署之前会考虑维持电压水平的问题；但这可能会迫使电动汽车行驶过长的距离才能到达充电站。类似的方法见于[35]，该研究使用北京市的真实出行数据来寻找最优位置，然而忽略了能源限制。在[36]中提出了功率损耗最小化，其中考虑了交通模式以最大化充电服务。然而，他们未考虑等待时间，也没有提供适应过程来应对未来几年增加的需求。在[37]中，尽管在部署充电站之前考虑了交通和电网约束，但他们没有考虑电动汽车负荷的进一步增加。

B. 问题定义与贡献

为应对上述挑战，我们提出了充电站定容与选址（CSDP）框架，以最低成本规划快速充电基础设施，满足电动汽车逐步接入所带来的充电需求。具体而言，该框架同时考虑充电站的选址（及容量）决策以及电动汽车充电负荷的分配，确保充电站的等待时间不超过最大可容忍值（即用户体验质量），并限制到达充电站的最大行驶距离。

我们的负荷分配方案还考虑了配电网络的电压水平，因此在设计阶段需决定是否配置最少数量的电压调节器（以最小化总体成本），以维持电压在可接受范围内。此外，我们确定支持充电站最大容量所需的变压器容量，并考虑每个配电网络的最大容量。最后，提出了两种不同的扩展模型以应对未来增长的能源需求，并将结果与两种提出的启发式算法进行比较。

我们工作的主要贡献是：
- 研究了快速充电站的部署与规模设定问题，在该问题中需保持最小等待时间和最短绕行距离。
- 综合考虑所需电压调节器数量和变压器容量，对这些充电站进行战略性布局有助于保持配电网中的电压水平稳定。
- 我们正式证明，仅考虑当前需求的CSDP问题解决方案可能导致未来现有基础设施的扩展成本较高。因此，我们研究了两种规划方法，以确定在需求增加情况下具有成本效益的CSDP问题解决方案：1）CSDP前向设计，该方法假设当前负荷来求解CSDP问题，并随着负荷增加逐步更新基础设施；2）CSDP逆向设计，该方法考虑未来需求以确定当前的部署策略。

本文的其余部分组织如下。第二节介绍了CSDP（充电站定容与选址）的系统模型，第三节描述了CSDP工作负载分配（CSDP-WA）和CSDP规模模型。第四节阐述了设施扩展方法，第五节给出了广泛的数值评估结果。最后，第六节进行了总结。

II. CSDP模型

我们考虑一个由单个电网供电的大都市，该电网具有确定数量的辐射状配电网。我们的目标是研究CSDP问题以确定

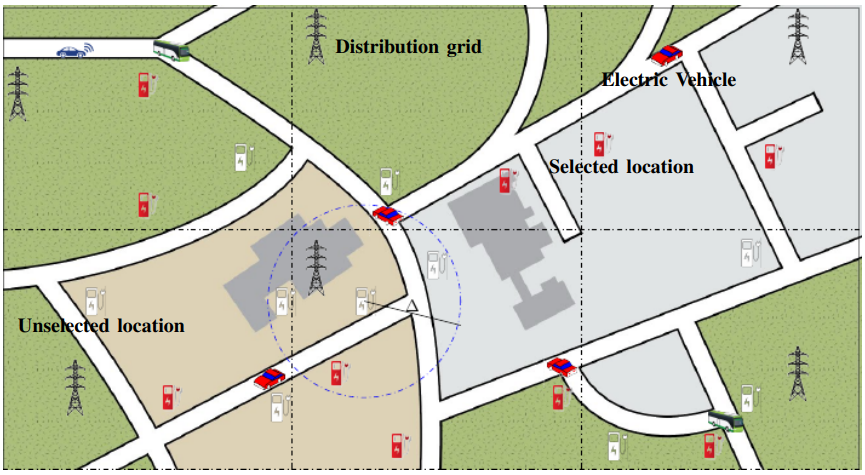
Grid
配电网 变压器
传统负荷 已部署的充电站降压 变压器
电压 调节器

通过充电站的最优部署，减少续航焦虑，并同时确保配电网各母线的电压稳定性。确定了电压调节器的最优数量和位置，同时还确定了每个充电站的变压器容量，以在其峰值需求下支持配电网容量。图1展示了需求区域和潜在位置，而图2展示了一个配电网络的示例。

A. 充电请求模型

我们假设城市中有 |E| 种类型的电动汽车，电动汽车的类型根据电池容量[38]确定（例如， e= 1代表小型电动汽车， e= 2代表中型，大型电动汽车由 e= 3表示）。现在假设该城市被划分为一组需求区域 Z（图1中的每个方格表示一个区域 z ∈ Z）。我们认为每个区域 z ∈ Z每小时具有平均电动汽车充电请求率σ z，其服从泊松分布[39]。该 σ z实际上是多个独立泊松分布的总和，即σ z = ∑e σ e z [40]。σ e z 表示来自区域 z的 e型电动汽车的充电请求率。每类电动汽车的能源需求假设服从均值为ω e 千瓦时的截断高斯分布[41]。此外，由于住宅建筑和工业的存在，每个区域 z还具有传统能源需求，可根据历史数据[42]进行预测。

B. 充电站模型

已假设市政当局主要选择一组位置 L 作为充电站部署的潜在位置（如图1中所示的红色和白色充电站）。如果某个位置被选中用于部署充电站（如图1中红色充电站所示），则需要确定在该位置 l ∈ L 部署的充电桩数量 pl。每个充电桩被视为三级快充设备，其充电速率假设为 α。为了最小化电动汽车驾驶员的续航焦虑，我们设定一个预定义的舒适行驶距离 ∆，即电动汽车不应被迫超过此距离才能充电。此外，我们设定最大允许等待时间 τ作为在充电站开始充电前的排队延迟。该等待时间取决于充电站 l 的电动汽车到达率(λl)以及部署在 l 的充电站的服务速率（单位时间内服务的电动汽车数量）µl。µl= f(pl, µ p l)取决于充电桩数量 pl 以及每个充电桩各自的服务速率 µp l 。

每个充电站被抽象为一个具有多个服务单元的排队系统，以确定等待时间（每个服务单元表示一个充电桩）。因此，我们假设每个充电站 l采用一个 M/M/pl队列，并根据公式(1)计算平均排队延迟 Wlq，其中 Nlq表示部署在 l 的充电站队列中的电动汽车数量， λl表示从不同区域 z到达该充电站的电动汽车到达率。

$$
Wlq=\frac{Nlq}{λl}; ∀l ∈ L \quad (1)
$$

其中 Nlq可通过以下方程[43]计算：

$$
Nlq=\frac{Plo( ∑z ∈ Zλ zl µ l )plΓl}{pl(1 − Γl)^2}; ∀l ∈ L \quad (2)
$$

其中， λzl 是区域 z 中分配给部署在 l 的充电站的电动汽车比例。 Γl 是该充电站处于繁忙状态（即无法立即为电动汽车提供服务）的概率， Plo 是该充电站没有电动汽车需要服务的概率。 Γl 和Plo 均取决于电动汽车到达率 λl、服务速率 µl 以及充电桩数量 pl，如公式 (3) 和 (4) 所定义：

$$
Γl=\frac{∑z ∈Z λzl}{plµl}; ∀l ∈ L \quad (3)
$$

$$
Plo= 1/\left[\sum_{m=0}^{pl-1}\frac{(plΓl)^m}{m!}+\frac{(plΓl)^{pl}}{pl!(1 − Γl)}\right]; ∀l ∈ L \quad (4)
$$

负荷分布 λ zl应符合用于减轻驾驶员里程焦虑的舒适行驶距离 ∆。因此，我们用 δ zl表示区域 z到充电站位置 l的距离，并通过计算 z中心到 l中心的欧几里得距离来得出该值。

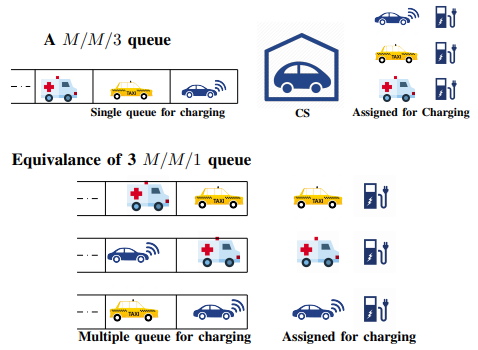
请注意，考虑使用 M/M/pl 模型来确定每个充电站的最佳位置和规模时，将包含一组非线性、非凸约束（公式(1)-(4)），以保持最小等待时间，因此该问题的求解可能在计算上难以处理，从而无法获得最优解。因此，为了简化起见，我们将 M/M/pl 排队模型近似为 pl 数量利用 M/M/1排队系统（如图3所示）来确定位置，然后返回到 M/M/pl排队系统以计算每个系统所需的充电桩数量。因此，我们分两个阶段求解该模型：i) 充电站部署问题工作负载分配（CSDP-WA）模型，ii) CSDP规模模型。这些CSDP-WA和CSDP-规模模型将在下一节中讨论。

C. 配电网络模型

我们还假设存在一组覆盖该城市的辐射式配电网 F 。每个网络 f ∈ F具有一组母线Nf，这些母线可同时承载电动汽车负荷和传统负荷，如图2所示。充电站将由现有的配电网络供电。由于L由市政当局确定，因此可以认为充电站 l在配电网f的母线 n上的可能分配位置是已知的。现在，为了支持负荷，需要采取一系列措施以实现电力平稳分配。

• 首先，要运行一个快速充电站，需要将线路电压降至 480V至600V的范围内[44]。图2显示，已部署的充电站通过一个降压变压器连接到母线10。该变压器的额定功率应取决于所连接充电站的峰值需求。图2中未显示为传统负荷提供支持的变压器，因为我们假设传统负荷所需的基础设施已经存在。
• 在辐射状网络的母线 n ∈Nf处建立由母线 l供电的充电站•，会降低该母线的电压水平，并影响网络中下游后续的各条母线。充电站中的每辆电动汽车均被视为有功负荷，因为电池充电产生的无功负荷极小，可忽略不计。因此，利用支路潮流方程[45]，我们可以确定任意配电网 f中任意母线 n的电压。配电网中每条母线 n的电压水平应维持在可容忍范围内。为维持电压水平 [46]，需在部分母线安装额外的电压调节器。图2中母线 8和母线17处的红色实心圆表示已安装的电压调节器，用于维持电压水平。
• 每个配电网变压器都有一个用于服务分配负载的最大容量。因此，为了遵守其最大容量限制，只能允许有限数量的充电站从特定配电网取电。

III. CSDP-WA 和 CSDP规模模型

为了避免计算复杂性，在设计CSDP-WA模型中的整数线性规划以确定充电站位置之前，将充电站视为总共pl M/M/1个系统，而非 M/M/pl 。在确定充电站的位置及其分配负载后，在每个位置应用启发式算法，以在 CSDP规模模型中计算所需的充电桩数量。整个过程如图 4所示，CSDP-WA模型和CSDP规模模型的具体细节将在接下来的小节中详细描述。

需求感知的电动汽车快速充电基础设施配置
假设一个 M/M/pl系统为 pl个 M/M/1系统
建立一个整数线性规划以最小化安装成本 其中等待时间被公式化 来自 M/M/1排队模型
使用Cplex求解整数线性规划以确定 充电站的位置及相应的分配负载
应用一种启发式算法 所有选定位置中的算法 确定最小数量 的充电桩数量以满足分配负载
Stop
CSDP − WA
CSDP Sizing

A. CSDP-WA 模型

为了克服 M/M/pl的难解性，主要涉及位置选择以及电动汽车向该位置的分配问题，我们将每个充电站的充电桩建模为一个 M/M/1队列（即用 pl 个 M/M/1的数量来近似M/M/pl ，如图3所示），从而能够获得可接受的平均排队延迟的更易处理的表达式。该方法还提供了在已部署的充电站中维持各充电站预定义等待时间所需的充电桩数量的上限（如图5所示），并且来自不同区域的充电请求率 σ z 应在已部署的充电站的安装充电桩之间进行分配。

模型的输入参数列于表I中。

表I 输入参数列表

输入符号	描述 & （单位）
L	部署充电站的潜在位置集合 l
Z	区域集合 z,电动汽车负荷将来自何处 分配到不同的充电桩
F	配电网 f的集合
Nf	配电网 f中母线 n的集合
P	充电桩 p的集合
p l max ∈ Z+	充电站在 l 的最大充电桩数量
σe z ∈ R +	区域 z ∈ Z 中 e 型电动汽车的充电请求率（请求/小时）
σz ∈ R +	区域 z ∈ Z 的电动汽车充电请求率为 σz=∑ e σ e z(请求/小时)
δ zl ∈ R +	区域 z 到位置 l 的距离（公里）
∆ ∈ R +	电动汽车充电的最大行驶距离（公里）
ζ zl	是一个二进制常数，如果 δ zl ≤ ∆, ζ zl = 1，否则为0
q f n l	是一个二进制常数，如果位置 l 由母线 n 供电网络 f, q f n l = 1 的，否则为0
P c f n ∈ R +	节点 n ∈ Nf 支持的常规有功功率 (kW)
Q f n ∈ R +	节点 n ∈ Nf 支持的常规无功功率 (kV A)
τ ∈ R +	电动汽车在充电站队列中的可容忍等待时间 (min)
ω e ∈ R +	e型电动汽车的平均能量需求 (kWh)
α ∈ R +	充电桩的充电速率 (kW)
α e ∈ R +	一种 e型电动汽车的最大充电速率（千瓦）
a l ∈ R +	位置 l 的土地成本($)
b ∈ R +	充电桩的成本 ($)
c k ∈ R +	额定容量为 T k 的变压器的成本($)
β ∈ R +	电压调节器的成本 ($)

1) 目标：最小化总部署成本。

$$
\min\left(\sum_{l \in L} Cl+\sum_{f\in F} \sum_{n \in Nf} C’ f n\right) \quad (5)
$$

其中 Cl表示在位置 l的充电站部署成本，C ′ f n 表示需要在配电网 f的母线 n处安装的附加电压调节器的成本。在描述约束条件后，我们将详细讨论该成本函数。

2) 充电站和充电桩部署约束：为了确定充电站的位置，定义了一个决策变量 γ l ，当选择位置 l用于部署充电站时为 γ l = 1，否则为0。

如果选择位置 l ∈ L 部署充电站，则需要配置一定数量的充电桩。我们假设有一组可用的充电桩 P，并定义一个决策二元变量 ρ l p，以确定是否在充电站 l 安装极数 p ∈ P（ρ l p = 1）或不安装（ρ l p = 0）。

$$
γl ≥ ρl p; ∀p ∈ P, ∀l ∈ L \quad (6)
$$

为防止充电桩被安装在多个位置：

$$
\sum_{l\in L} ρl p ≤ 1; ∀p ∈ P \quad (7)
$$

每个位置 l 都有用于部署的空间容量，且式(8)确保位置 l 处的充电桩总数不得超过其最大容量。

$$
\sum_{p\in P} ρl p ≤ pl max; ∀l ∈ L \quad (8)
$$

3) 服务速率约束：回顾一下，每个充电桩 pl 被抽象为一个M/M/1 队列，为了衡量充电桩的服务速率，需考虑分配给电动汽车的加权平均需求 ωp 和充电速率 αp 。这些加权值取决于各类电动汽车的比例。

$$
ωp= \frac{\sum_e\left(ωe\sum_z λ e zp\right)}{\sum_e\sum_z λ e zp}; ∀p ∈ P \quad (9)
$$

$$
αp= \frac{\sum_e\left(αe\sum_z λ e zp\right)}{\sum_e\sum_z λ e zp}; ∀p ∈ P \quad (10)
$$

其中 ωe是 e型电动汽车的平均能量需求，αe是 e型电动汽车的平均充电速率。而 λe zp 表示从区域 z到充电桩 p的 e型电动汽车到达率。

$$
µ p ≤ \frac{α p\sum_{l\in L} ρl p}{ω p}; ∀p ∈ P \quad (11)
$$

其中 µ p是充电桩 p的服务速率。

4) 电动汽车负荷分配约束：我们应配置足够的充电基础设施，以支持所有区域的全部电动汽车负荷。

$$
\sum_{p\in P} λ e z p ≥ σ e z ; ∀z ∈ Z, ∀e ∈ E \quad (12)
$$

我们假设从区域 z到位于位置 l部署的充电站的任意充电桩 p的距离是均匀的，并用 δ zl表示。因此，只有当距离 δ zl不超过 ∆时，区域 z中的部分电动汽车负荷才能被分配到 l处充电站的充电桩 p 。以下约束条件可避免电动汽车车主为充电而进行长距离驾驶。

$$
λ e z p ≤\sum_{l \in L} (ρ l p ζ zl) σ e z ; ∀p ∈ P, ∀z ∈ Z, ∀e ∈ E \quad (13)
$$

其中 ζ zl 是输入二进制系数，当 δ zl ≤ ∆时为 ζ zl = 1，否则为0。δ zl 表示从 z到 l的距离。

5) 延迟约束：我们考虑任意电动汽车在任一桩位的允许等待时间 τ；因此，每个桩位被建模为一个 M/M/1 队列。我们的模型确保在每个桩位 p，电动汽车的最大等待时间不应超过值 τ。

$$
\frac{1}{µp −\sum_{z\in Z}\sum_{e} λ zep} ≤ τ; ∀p ∈ P \quad (14)
$$

为了维持稳定队列，我们认为服务速率必须大于电动汽车到达率。

$$
µp −\sum_{z\in Z} \sum_{e} λe zp ≥ 0; ∀p ∈ P \quad (15)
$$

6) 电压调节器布置和分接头定位约束：任何辐射状配电网 f中每个母线 n的电压应保持在可容忍范围内，如公式(16)所示。

$$
Vmin ≤ Vfn ≤ Vmax; ∀f ∈ F, n ∈Nf \quad (16)
$$

任何母线 n的电压 Vfn均可根据方程(17)[45]计算得出：

$$
V^2_{f(n+1)}= V^2_{fn} − 2(rfnPfn+ xfnQfn)+\frac{(r^2_{fn}+ x^2_{fn})(P^2_{fn}+ Q^2_{fn})}{V^2_{fn}}; ∀n ∈Nf, ∀f ∈ F \quad (17)
$$

其中， rfn+ jxfn 是网络 f 中从母线 n 到母线 n+1 的线路阻抗， Qfn 表示无功功率流，Pfn 表示有功功率流。由于已部署的充电站，辐射状网络 f 中母线 n 的有功功率 Pfn 可能增加，并可通过方程(18)计算。

$$
Pfn= P c fn +\sum_{l\in L} q_{fn l}\left(\sum_{p\in P} ρl p\right)α; ∀f ∈ F, n ∈Nf \quad (18)
$$

由于式(17)是非凸的，模型的求解变得难以处理。我们受到[47]的启发，采用一种近似方法来估计辐射状配电网的母线电压。该近似方法基于两个条件[47]：
1) 功率损耗相对于有功功率和无功功率流足够小，即 $\frac{(r^2_{fn}+x^2_{fn})(P^2_{fn}+Q^2_{fn})}{V^2_{fn}} = 0$。
2) 电压偏差非常小，相对于假设$(Vfn − V0)^2= 0$。

因此，可以从公式(17)得到以下线性形式。

$$
V_{f(n+1)} = V_{f n} − \frac{(rf n P f n + x f nQf n)}{V_{f 0}} ; ∀n ∈Nf , ∀f ∈ F \quad (19)
$$

其中 V f 0是网络 f的电源电压，假设其已知。该潮流方程的线性形式首次在[48]中提出。现在，由于我们假设为大都市，线路损耗相较于充电站负荷[49]非常小，并且模型保持电压水平处于可接受范围（[Vmin = 0.95 p.u., Vmax = 1.05 p.u.]）内，因此可以采用此近似方法。

现在，一旦在 f 网络的 n 节点部署了充电站，负荷将增加，电压水平将下降。因此，每当附加的已安装的充电站负荷导致母线 n或网络 f中后续母线的电压水平降至最低可容忍水平 Vmin以下。为此，一个二进制变量 yfn用于确定是否安装电压调节器，即当需要在网络f的母线 n处安装电压调节器时为 yfn= 1，否则为0。

电压调节器实际上是一种有载调压变压器，通常每个分接头都会对电压水平产生一定量的变化（例如，在常规的电压调节器中有32个分接头；16个正向和16个负向[50]。因此，每个分接头会使电压水平变化5%到8%[50]）。为了确定所安装电压调节器的分接头位置，声明了一个离散变量 tr ∈[−tmax, tmax]。现在，为了维持电压水平，该模型遵循以下约束条件。

$$
Vmin ≤ Vfn+ yfn\left( \frac{tr}{tmax} \right)Vf(n−1) ≤ Vmax; ∀f ∈ F, n ∈Nf \quad (20)
$$

7) 充电站变压器容量约束：为了支持在位置 l新部署的充电站，需要部署一个降压变压器以匹配所需的电压水平。该变压器的额定功率取决于该位置 l充电站的峰值需求。已安装的降压变压器的额定功率为：

$$
α\sum_{p\in P} ρl p ≤\sum_{k} ηl ktk; ∀l \quad (21)
$$

其中 ηl k是一个决策二元变量，当位于l的充电站的降压变压器额定功率为tk ∈ Tk={3kV A, 6kV A, 9kV A, 15kV A}[44]时 ηl k = 1，否则为0，其中 k ∈{0, 1,…, |Tk|}。现在，为了防止某个变压器出现多个容量等级，模型需遵守以下约束。

$$
\sum_{k} ηl k= 1; ∀l ∈ L \quad (22)
$$

8) 配电网变压器约束：每个配电网变压器都有一个最大容量，用于满足充电站需求以及传统电力需求，为简化起见，我们假设该容量值为 Dmax。因此，总需求（传统负荷和充电站负荷）不得超过 Dmax的值。

$$
\sum_{n} (Pf n + Qf n) ≤ Dmax ; ∀f ∈ F \quad (23)
$$

9) 成本函数：根据公式(5)，目标是最小化总成本。

C l表示在 l安装一座充电站的安装价格。这取决于位置价格 a l 、充电桩数量∑p ∈ P ρ l p以及每个充电设备的成本 b。该 C l 还取决于所安装降压变压器的价格，而该价格又取决于额定功率 t k 。公式(24)表示 C l 的值。

$$
C l = γ l a l +\sum_{p \in P} ρ l p b+\sum_{k} (η l k c k) ; ∀l ∈ L \quad (24)
$$

其中 ck是安装额定功率为 tk的降压变压器的成本。另一方面，电压调节器的安装成本可表示为：

$$
C′ fn= yfnβ; ∀n ∈ Nf, ∀f ∈ F \quad (25)
$$

其中 β表示电压调节器的成本。

一些约束是非线性的，我们需要将其线性化。由于公式 (9)、(10)和(11)中包含两个连续变量的乘积，因此具有非线性特性，我们采用McCormick包络近似[51]来实现线性化。另一方面，公式(20)由于包含一个二元变量与一个连续变量的乘积，也是非线性的，因此可以通过[52]进行线性化。

B. CSDP容量规划模型

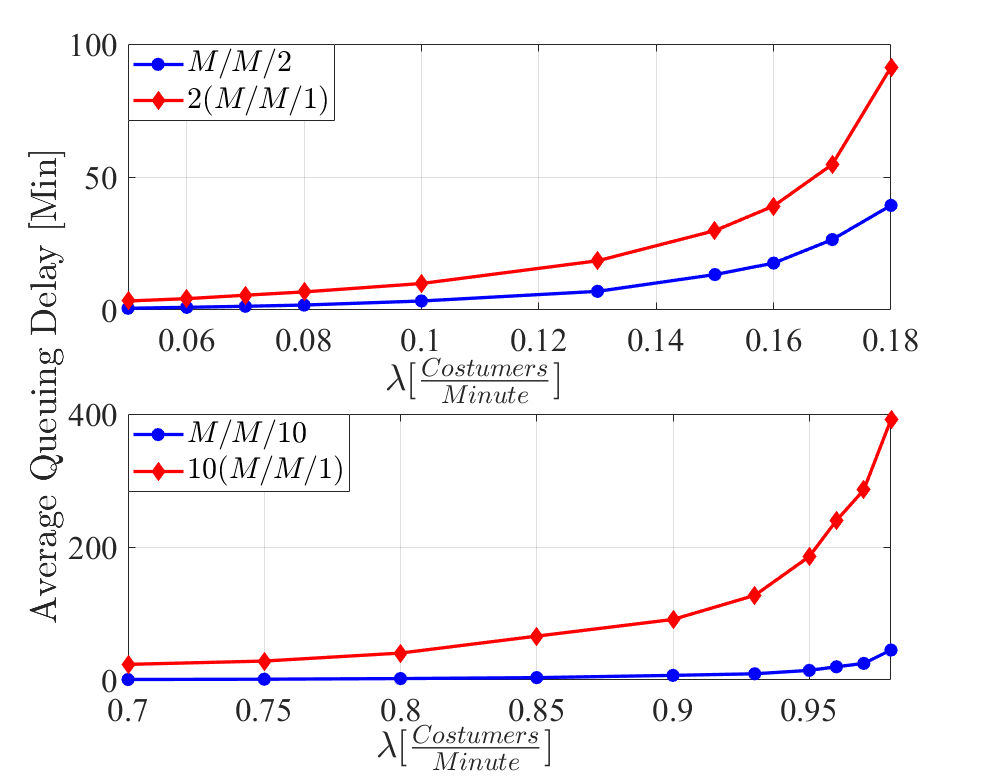
如前所述，为了克服延迟约束表达式的复杂性，我们通过 pl个 M/M/1系统来近似建模充电站（CS），其中每个 M/M/1表示每个充电站的一个充电桩。这使得我们可以使用公式(14)来建模充电延迟，从而更易于处理。然而在实际中，充电站通常应具有单个队列。因此， M/M/pl是一种更为真实的模型。需要注意的是，我们基于 pl个M/M/1队列的设计会导致充电站资源配置过度（即充电桩数量过多），因为 pl个 M/M/1的延迟是 M/M/pl的上界，如图5所示。为缓解这一问题，我们开发了一种方法，为每个充电站配置足够（刚好足够）的充电桩以满足分配的工作负荷。换句话说，我们采用 CSDP-WA模型得出的负荷分配和充电站选定位置的解，并在每个充电站逐步增加充电桩，以满足工作负荷的需求，同时满足充电延迟τ。具体细节见算法1。

算法1 CSDP容量规划模型
1: 设置 p max l = pl, ∀l ∈ L（来自CSDP-WA模型）
2: 设置 l= 1
3：如果 γl = 1，则转到第 5 步；否则 l++
4：如果 l ≤ |L|，则转到步骤3；否则转到步骤10
5：设置 pl = 1
6：使用 M/M/pl排队计算新的延迟时间 τ′ 系统
7: 如果 τ′ ≤ τ，则将 pl 作为所需的充电桩数量并进行下一步到步骤9；否则 pl ++
8: 如果 pl ≤ p max l ，则转到步骤6
9: l++并转到步骤4
10: 退出

IV. 扩展模型

随着电动汽车负荷需求预计在未来几年内增加，公共充电站的建设应适应这一预期增长。事实上，我们可以预测未来的电动汽车负荷（例如，未来10‐20年），但根据未来需求一次性安装所有充电站可能不具备成本效益，因为许多充电站在应对当前需求时将处于闲置状态。因此，逐步扩展充电设施是明智之举。为此，我们提出了两种不同的设计方案：CSDP前向设计和CSDP逆向设计用于处理充电站的扩建。

A. CSDP前向设计

假设从 i年到 j年采取逐步的充电站部署，且分辨率为 k年（即每隔 k年进行一次新的部署）。现在，在 CSDP前向设计中，我们基于 i年的当前需求，使用所提出的模型选择一组位置 Li ⊂ L来安装充电站，而不考虑未来的需求增长。然后，在i+ k年，该基础设施将无法满足过大的电动汽车负荷需求。因此，我们使用CSDP-WA和CSDP容量规划模型来决定在 l ∈{L − Li}处需额外部署的充电站数量，并重新确定在 l ∈ Li处已部署充电站的容量。此方法将持续实施至j年。该设计在算法2中进行了详细说明。这种方法非常直接，尽管预期初始安装成本较低，但从长远来看并不能保证总成本更低。

算法2 CSDP前向设计
1：初始化第m年=i
2：确定所需数量的位置和容量 基于 m年的需求的充电站数量 Lm ⊂ L
3：如果已过去 k年，则设置 m= m+ k
4: 如果 m ≤ j，确定新的充电站集合 Lm ⊂{L−Lm−k}， 重新计算{Lm−k}; ∀k 的容量，并转到步骤3； 否则转到步骤5
5：退出

B. CSDP逆向设计

在本设计中考虑了未来几年的预期需求。首先，我们根据 j年的预测负荷选择一组位置L′ j ⊂ L。然后，针对j − k年进行需求预测和位置选择，使得L′ j−k ⊂ L′ j。该过程同样应用于 j − 2k，其中 L′ j−2k ⊂ L′ j−k，并持续进行直到 j − nk> i。现在，我们选择位置集合 L′ i ⊂ L′ j−nk以满足 i年的当前需求。经过 k年后，我们可以在 l ∈{L ′ j −(n−1)k −L ′ i}部署新的充电站，因此预计其在未来需求适应性和长期成本效益方面更具优势。算法3详细阐述了该设计。

算法3 CSDP逆向设计
1：初始化年份 m= j
2: 预测 m年的需求
3：确定一组位置的位置和容量 L ′ 基于 m年的需求
4: 设置 m= m− k并预测 m年的需求
5：如果 m ≥ i，确定充电站集合 L ′ m ⊂ L ′ m+k并转到步骤4; 否则转到步骤6
6：退出

五、实证评估与讨论

A. 数据分析

为了评估CSDP方法的性能，我们考虑一个类似蒙特利尔的电动汽车普及型城市。蒙特利尔的总面积为431平方公里，人口为178万。现在要确定该城市的电动汽车充电需求，需要进行广泛分析，特别是目前尚未针对蒙特利尔开展充电站部署问题的研究。根据我们的模型，假设该城市被划分为19个不同区域（例如|Z| = 19），类似于蒙特利尔的19个区[53]。每个区具有不同的面积和人口密度。为了确定每个区的电动汽车数量及其相应的出行情况，我们复现了一项研究工作[54]，该研究分析了蒙特利尔某一地区（居民数为37767）的电动汽车渗透率及其对电网的影响。为了估算电动汽车渗透率，他们考虑了蒙特利尔现有的全部21种电动汽车，并基于该地区居民的社会经济地位，假设了每种电动汽车的渗透水平。他们的研究发现表明，整体电动汽车渗透率为10%，如果城市经济部门没有发生剧烈变化，则有可能达到86%。因此，我们可以假设蒙特利尔的电动汽车总数为90900辆（按10%渗透率计算），其中约42%为纯电动汽车，且配备不同容量的电池[54]。由于我们计划部署若干快速充电器，在本研究中应仅关注纯电动汽车（本文中简称为EV），而不考虑插电式混合动力汽车。现在，根据电池容量，我们将这些电动汽车分为三大类[14]：

表I 电动汽车类别

电动汽车类型	小型	Mid	大型
电池容量（千瓦时）	24 − 60	60 − 85	≥ 85

根据人口密度，我们可以假设蒙特利尔19个区域中各类电动汽车的数量，其中小型电动汽车约为14,500辆，中型电动汽车为3,000辆，其余为大型电动汽车[54]。除了确定整个城市电动汽车的分布外，还需研究出行行为和充电习惯，以估算每个区域的充电需求。目前，此类行为分析已在[55]中进行，该研究以斯德哥尔摩市为例，评估其提出的部署若干快速充电器的算法。尽管斯德哥尔摩（231平方公里）的面积约为蒙特利尔的一半，并且将城市划分为12个区域，但两座城市的人口密度几乎相同。此外，这两座城市在气候和社会经济状况方面也有许多相似之处，因此我们在本研究中采用了他们的方法来确定充电需求。预计约有40%的电动汽车将在公共充电设施充电[55]，蒙特利尔电动汽车在家的平均出发和返回时间分别为上午8点和下午6点[54]。因此，我们预计在蒙特利尔从上午8点到下午6点期间，可能有4560辆电动汽车尝试在公共充电站充电，并假设这些车辆均匀分布在城市的19个区域中。

我们还假设每辆电动汽车的能源需求服从均值为 ω e 的截断高斯分布[41]，其中 e型电动汽车的千瓦时（其中 e= 1表示小型， e= 2表示中型， e= 3表示大型电动汽车）。我们假设市政当局已初步选定了40个部署充电站的潜在位置（ |L| = 40），计划安装最多200个充电桩（|P| = 200），且任何充电站的最大允许等待时间不应超过 τ分钟。

采用归一化值来表示安装成本。为了对价格进行归一化处理，设定$ x为单个电压调节器的价格，其他实体的价格则按比例相对于$ x表示。例如，土地成本因地点而异，假设其服从均值为$ 20x、方差为$ 5x的高斯分布。对于传统有功和无功功率，我们采用IEEE 33节点系统的数值。基于上述假设，我们评估这些参数对两阶段 CSDP解决方案（CSDP-WA和CSDP-规模）的影响，并评估两种规划方法，以在需求增加的情况下确定CSDP问题的成本效益解决方案。我们还提出了两种启发式方法： 1）最大位置优先选择（LLSF）和2）最便宜位置优先选择（CLSF），并将其与CSDP进行比较。该模型在配备 3.40吉赫英特尔酷睿i7‐6700处理器的C++平台上，使用 IBM Cplex优化器求解。最后，开发了一个基于 PYTHON的自定义离散事件仿真器，用于在实际场景中评估这些解决方案。

B. CSDP容量规划模型的性能评估

为了评估CSDP-容量规划方法在成本降低方面的性能，我们确定了充电站的最优位置及其分配的电动汽车负荷，条件为 τ= 9分钟和 ∆= 3公里。在获得 CSDP-WA模型提供的电动汽车工作负载分配和位置选择的解之后，将CSDP-容量规划方法应用于每个选定的位置。CSDP-规模问题显著减少了维持该排队延迟所需的充电桩数量。图6显示，通过CSDP-WA问题选出了9个位置，并且CSDP-规模方法减少了所有充电站所需的充电桩数量。对于某个特定的充电站，最多可减少45%的充电桩，从而整体安装成本降低了27%。为了评估所提出模型的有效性，开发了一个自定义的基于Python的离散事件模拟器。根据给定的解决方案，将100万个样本电动汽车分布在上述 9个充电站中，模拟器提供了所有车辆的平均等待时间。表III所示的结果表明，所有充电站均能够满足预设的最大等待时间（τ= 9分钟）。

C. 不同参数的经验评估 rs

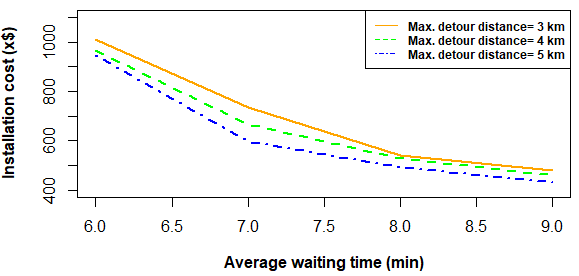
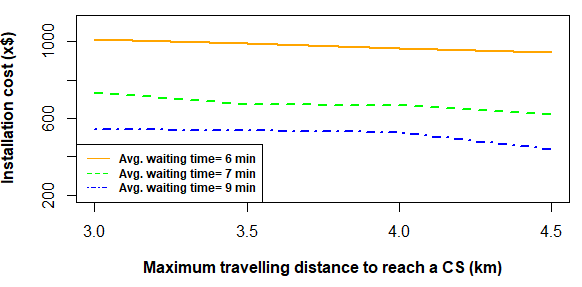
作为充电设施配置模型，保持更严格的等待时间需要安装更多且容量更高的充电站。图7显示，对于 ∆= 3，当允许的最大等待时间为7分钟时，所需成本为$ 678x，而当等待时间增加到9分钟时，成本变为$ 478x。或者，在服务速率较慢的情况下，只要将等待时间增加到9分钟，仍足以维持相同的能源需求，从而减少所需的充电站数量。图8显示，需要选定位置以确保 τ= 7分钟的等待时间，而9个位置足以满足 τ= 9分钟的等待时间（为简化起见，图8中仅标示了选定的位置，未显示其容量）。因此，仅将允许的最大等待时间增加2分钟，即可实现安装成本降低29.8%。但该成本降低率与等待时间的增加值之间并不呈现线性关系。例如，将等待时间从6分钟增加到7分钟，可节省约40%的总成本。随着等待时间进一步增加，这种成本降低幅度逐渐减小，这一发现对于确定一个既具有成本效益又可被消费者接受的最大等待时间具有重要意义。图7还表明，电动汽车为到达充电站所需行驶的绕行距离（∆）也会影响安装成本。

根据图7，为了保持固定的等待时间，较短的距离会导致更高的安装成本。例如，图9显示，对于6分钟的等待时间，当最大行驶距离从3公里增加到3.5公里时，总部署成本从 1010x降低至 990x。这是因为当电动汽车的最大行驶距离为3.5公里而非3公里时，只需19个充电站即可满足所有电动汽车的需求，而不是20个。安装成本的降低率随着绕行距离的增加几乎呈线性下降，但这种变化趋势不如等待时间的影响显著。

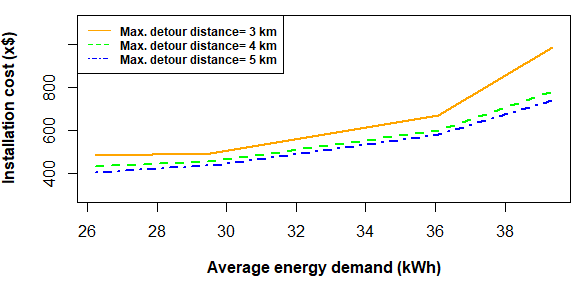
安装价格还受到每辆电动汽车平均能量需求的影响。平均能量需求取决于不同类型电动汽车的比例以及每种类型电动汽车的均值需求。随着平均能量需求的增加，平均充电时间也随之增加，因此需要部署更多的充电站以保证预设的等待时间，从而导致安装成本也相应增加。例如，图10显示，在等待时间为9分钟、到达充电站的最大绕行距离为5公里的情况下，当平均能量需求从26.2千瓦时增加到29.5千瓦时，总部署成本从$ 404x增加至$ 439x。

我们的模型还考虑了充电站安装对现有配电网络的影响，并确定在最佳位置安装最优数量的电压调节器，以最小化总体成本。同时，也确定了电压调节器相应的分接头位置。现在，

表III 评估CSDP-容量规划方法的性能

位置	CSDP-WA	CSDP-规模	时间（分钟） 用于 CSDP-WA	时间（分钟） 用于 CSDP-规模
0	6	4	4.05	1.53
12	11	6	4.25	3.61
13	8	5	4.22	1.67
15	9	5	4.21	3.79
17	10	6	4.23	1.8
23	11	6	4.23	3.7
27	9	6	6.07	2.96
32	7	4	4.16	4.09
36	8	5	4.24	1.81

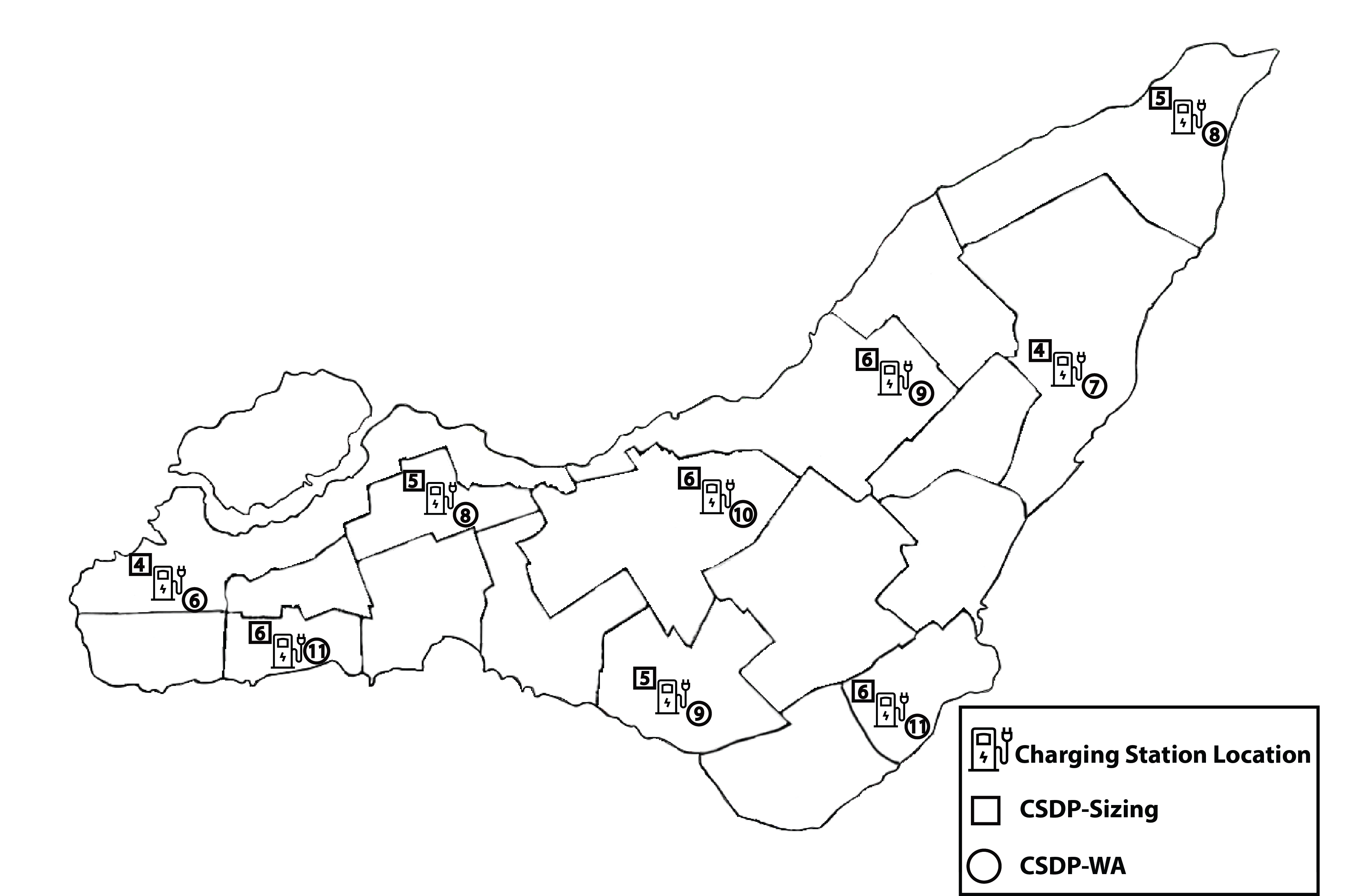
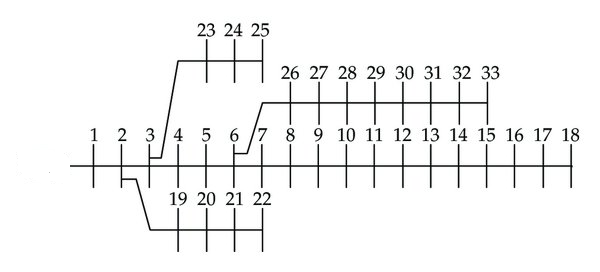
已部署的充电站可能会降低配电网的电压水平。对充电站进行战略性选址有助于减轻对母线电压水平的影响，并减少所需的额外电压调节器数量，从而降低部署成本。图 11展示了辐射状网络0（f= 0）在该场景下所有33条母线的电压水平，其中2个充电站接入母线2，另一个充电站接入同一条辐射状网络的母线4（考虑每个充电站的最大需求）。由于网络需要为这些充电站提供额外负荷，母线7 和22的电压水平下降至0.95标幺值以下（0.95标幺值为最低要求电压，在图11中以绿色虚线表示）。因此，为了电压稳定性，必须在这些母线上安装电压调节器。安装在母线7的电压调节器将其分接头位置设为2，而另一个电压调节器的分接头位置为1。

D. 分析充电基础设施扩展方法

对于充电站网络的逐步扩展，我们提供了两种不同的设计：CSDP前向设计和CSDP逆向设计。为了比较这两种设计，我们假设电动汽车普及率从第1年（当前年份）到第2年增加25%，并在第3年再增加25%。同时，我们假设传统负荷在第2年增加5%，到第3年累计增加10%。为简化起见，我们采用恒定的 ∆= 3 km和 τ= 9 min值。在应对初始需求方面，由于CSDP逆向设计强制选择8个昂贵的位置而非较便宜的选项，其初始安装成本略高（图12）。图13展示了选定的位置及其相应规模。该 CSDP逆向设计逐渐证明自身具有成本效益。事实上，针对第2年的需求，它几乎可降低成本14%

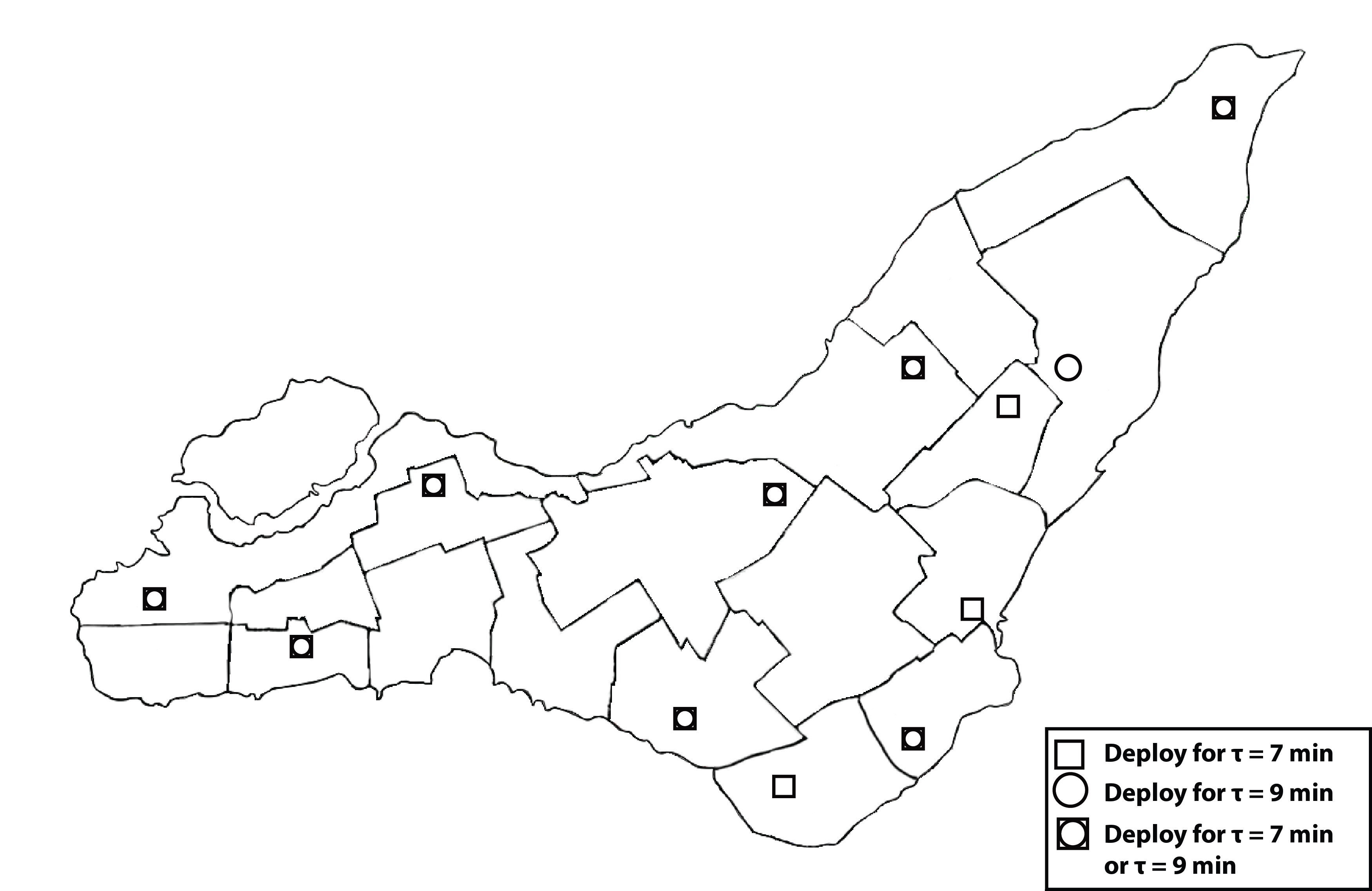
通过部署11个充电站，而CSDP前向设计建议选择12个位置，原因是需考虑第1年安装的所有充电站。对于第3年，成本降低接近11%。因此，从短期来看，考虑未来负荷似乎效率不高，但从长远来看，更具成本效益。

E. 对比分析

最后，我们将我们的CSDP模型与两种启发式方法进行性能比较：最大位置优先选择（LLSF）和最便宜位置优先选择（CLSF）。LLSF的核心思想是选择较大的位置（即可以安装更多充电桩）来部署足够数量的充电站。因此，对于极数 p l max 最大的位置 l，在部署充电站时具有最高优先级。另一方面，最便宜位置优先选择首先选择成本最低的位置。这意味着应首先选择价格 al最小的位置 l。图14展示了三种不同平均等待时间下的成本变化情况。我们的CSDP模型在两种启发式方法中表现更优。例如，为了维持τ= 6分钟的平均等待时间，CSDP选择了20个位置，而最大位置优先选择也选择了20个不同的位置（但它选择了成本较高的位置5和8，而不是更便宜的位置4和 32）。另一方面，最便宜位置优先选择必须选择24个位置。

VI. 结论

提出了一种两阶段模型，用于解决充电基础设施设计问题，该模型能够在最低部署成本下确定最优位置和容量（充电桩数量）。考虑到充电的舒适行驶距离和可接受的最大等待时间，使该模型对电动汽车驾驶员具有吸引力。为了确定充电站的等待时间，我们将每个充电桩建模为一个服务节点，并使用排队论来估计电动汽车充电的等待时间。CSDP-WA方法采用M/M/1排队论估算等待时间以确定充电站的最优位置；在确定位置后，CSDP-规模方法在分配的电动汽车上应用M/M/c排队论以确定所需的充电桩数量。鉴于大规模部署充电站可能会降低配电网络任一节点的电压水平，为保持其稳定性，我们考虑安装电压调节器（如需要）并确定相应的分接头位置。战略性充电站部署能够减少所需电压调节器的数量，从而降低成本，并在此测试了IEEE 33节点系统。我们还确定了变压器容量以支持已安装的充电站，同时考虑配电网的容量以避免负载拥塞。我们还研究了两种不同的充电站扩建设计方案，以满足预期增长的需求。尽管CSDP逆向设计初期成本较高，但从长期来看，其在成本最小化方面表现优于CSDP正向设计。我们还提出了两种启发式方法（LLSF、CLSF）来评估CSDP模型的性能。最后，开发了一个定制的基于 Python的离散事件模拟器来测试这些方案。然而，此类大规模充电站与电网的集成也可能导致显著的功率损耗，并在负荷曲线上引入新的峰值。因此，在未来的研究中，我们将致力于探究大规模快速充电站渗透可能带来的负面影响，并尝试确定可能的缓解措施。