三杯风速计低功耗检测算法

一种用于三杯风速计的自适应低功耗检测算法的设计与验证

摘要

设计了一种用于杯式风速计的自适应低功耗检测算法。在恒定风场的仿真中应用了商用杯式风速计的模型。当杯轮旋转在风场中稳定后，其转速会在一定范围内波动。研究发现，转速分布近似符合正态分布模型，并获得了该模型在不同风速下的参数。基于此分布模型，为杯式风速计设计了信号处理算法，并设计了适配该算法的信号处理结构。实验表明，该算法具有较强的适应性，能够保持风速计的性能。该风速计实现了低于4.2mW的低功耗，在0.9米/秒至10米/秒的测量速度范围内，平均速度误差小于0.25米/秒。

引言

风速测量在气象学、风电产业、建筑业、农业和交通运输等多个行业中一直具有重要意义。风速通常由风速计进行测量。风速计可能被安装在电源供应不便且无法保证频繁维护的地方，例如山区、海上或无人区。在这些情况下，风速计的电源来自电池，而有限的电池电量会影响其工作时长。因此，需要一种低成本、低功耗风速计来实现长期大规模风速测量。

市场上主要有3种类型的风速计，分别是超声波、热式和机械式风速计。超声波风速计具有高精度、宽测量范围，并且不受机械磨损影响[1–4]，但其脆弱性和高制造成本限制了其在恶劣环境中的大规模应用[5–8]。通常，热式风速计体积小、对环境温度变化敏感，并且能够对风速变化响应快[9–11]。由于温度和灰尘会影响热式风速计的检测，因此其在大范围温度变化的开放场景中的应用受到限制[12,13]。

机械式风速计，包括杯式风速计和螺旋桨式风速计，可能是大多数条件下应用最广泛的。它们通常便宜、可靠且易于安装[14–19]。同时，杯式风向标比螺旋桨式成本更低，互换性更好[20]。因此，杯式风速计更常用于测量风速。

经过考虑，低功耗杯式风速计更适合在不同条件下进行风速测量。通过对商用杯式风速计进行建模并借助仿真，本文提出了一种针对光电杯式风速计设计的自适应低功耗算法。该算法随后应用于信号处理结构和电路经过重新设计的模拟风速计中。实验结果表明，提出的杯式风速计具有更低的功耗并实现了更优的性能。

本文其余部分组织如下。第2节在CFD软件中模拟杯式风速计在不同风场下的旋转情况，分析仿真结果并确定杯式风速计的运动规律。在第2节中，基于第2节得出的杯式风速计运动规律，提出了一种用于光电式杯式风速计的自适应低功耗算法，并重新设计了杯式风速计的信号采集与处理结构，以便应用所提出的自适应低功耗算法。所提出的杯式风速计的性能测试结果在第4节中给出，最后在第5节中得出结论。

2. 分析

杯式风速计的基本工作原理在于风杯转子的线速度与风速之间的关系。风洞试验给出了风速u与风杯转子的线速度uc之间的线性关系，如（2‐1）[20,21]，

$$
u = a + buc + cuc^2 \quad (2-1)
$$

其中杯式风速计的启动风速为a，风速系数为b，二次系数为c。由于c通常是一个很小的变量，因此可以忽略二次项[20]。

由于风杯转子的线速度与其角速度之间存在对应关系，(2-1)可转化为(2-2)，其中n为杯式转子的角速度，k为旋转系数。这样就建立了风速与杯式转子的角速度之间的关系。

$$
u = a + kn \quad (2-2)
$$

这表明风杯转子是杯式风速计的关键部件，其在风场中的运动直接影响风速计的性能。因此，有必要研究风杯转子在风场中的运动，其中风洞试验和理论分析是两种最常用的研究方法。风洞试验成本较高且耗时较长，而理论分析则包含大量简化条件和假设。这些不足可通过计算流体动力学（CFD）[22]加以解决。因此，采用CFD来研究风杯转子的运动。为确保分析结果的精度，选用一款商用三杯风速计进行建模和数值模拟。

在CFD软件中建立了杯式风速计的模型和虚拟风洞。虚拟风洞的长度（x）、高度（y）和宽度（z）分别设置为3米、2米和2米。此外，流体材料为空气，风杯转子由碳纤维制成。该实体的行为遵循刚体动力学，且忽略摩擦扭矩。尽管风杯转子不能平移，但它可以在恒定风速下从静止状态绕z轴旋转至稳定状态。CFD软件可以输出风杯转子的实时角速度（见图1）。

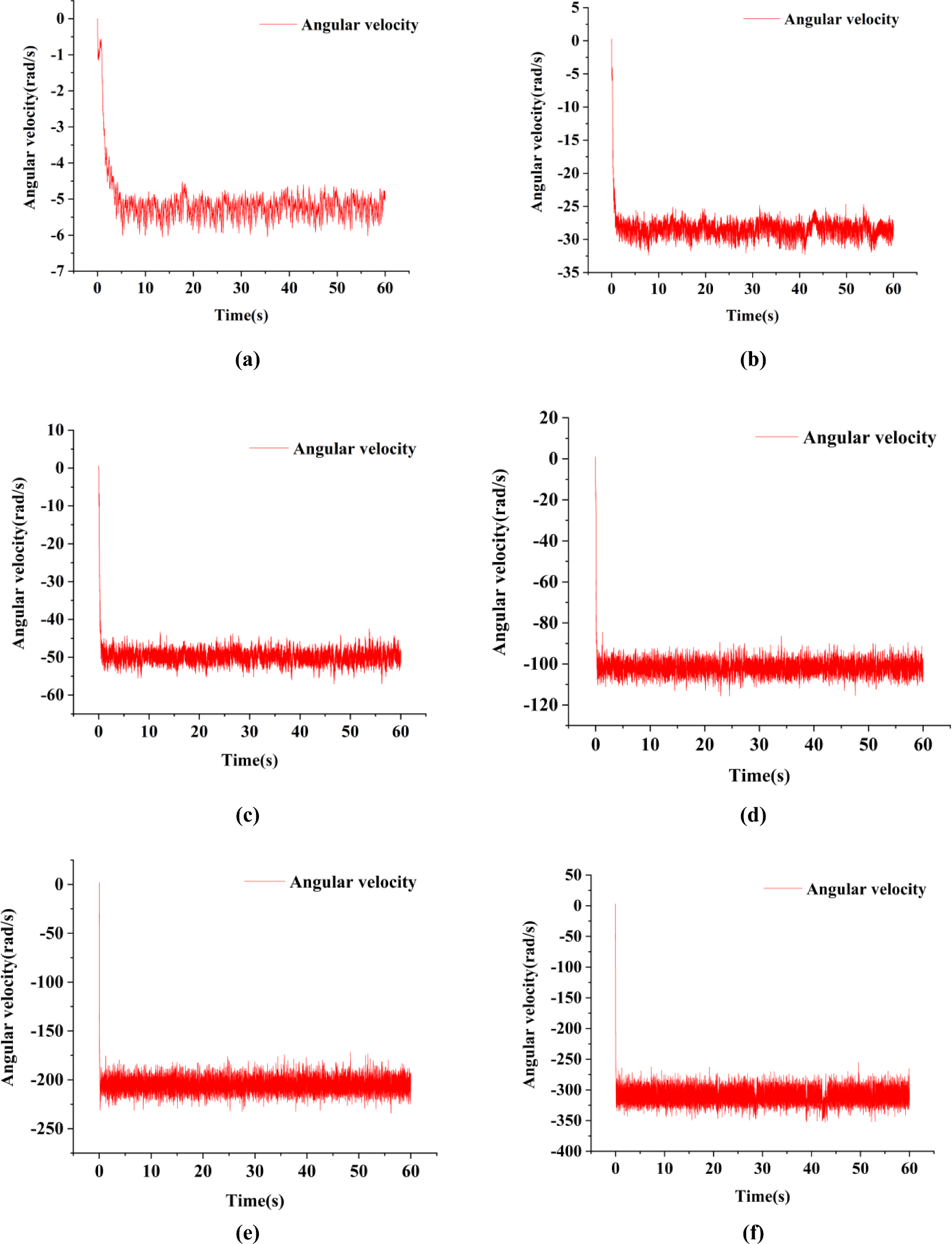
随后，对风速从0.7米/秒至30米/秒时杯轮旋转的仿真进行了模拟，结果如图2所示。结果表明，在不同风速下，风杯转子首先经历一个加速过程。加速完成后，其旋转速度将在一定范围内上下波动。这是由于风场中三个风杯转子所受力的作用不同所致。

0.7 米/秒 (b) 3 米/秒 (c) 5 米/秒 (d) 10 米/秒 (e) 20 米/秒 (f) 30 米/秒时角速度的仿真结果。)

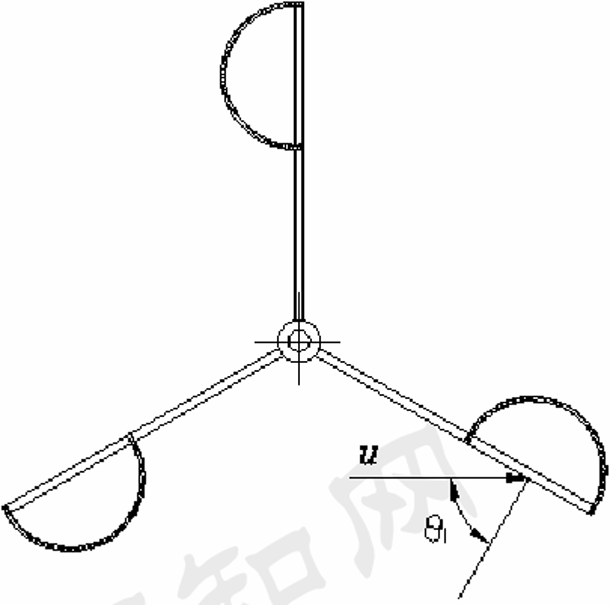
图3显示了一个典型的三杯风速计的结构示意图。假设外部风速u是恒定的，空气相对于第i个杯式转子的相对速度为：

$$
u_{ri} = u - 2\pi nR\cos\theta_i \quad (2-3)
$$

在此方程中，$\theta_i$ 是风速与杯式转子i的法线之间的角度，n是风速计的速度，R是杯式转子的回转半径。因此，单位时间内作用在杯式转子上的空气的有效质量为$AC_n(\theta_i)\rho u_{ri}u$，其中$C_n(\theta_i)$表示杯式转子平面法线与风矢量之间的角度为$\theta_i$时，空气有效质量系数。

杯式转子组由三个以120°角度相互连接的杯式转子组成。当角度分别为$\theta_i$、$\theta_i + 120^\circ$和$\theta_i + 240^\circ$时，整个转子组上的瞬时风压等于三个杯式转子上压力的总和。方程如下：

$$
a_i = C_n(\theta_i) + C_n(\theta_i+120^\circ) + C_n(\theta_i+240^\circ) \quad (2-4)
$$

$$
b_i = C_n(\theta_i)\cos\theta_i + C_n(\theta_i+120^\circ)\cos(\theta_i+120^\circ) + C_n(\theta_i+240^\circ)\cos(\theta_i+240^\circ) \quad (2-5)
$$

在此方程中，$a_i$是风速计组的压力系数，而$b_i$是阻力系数。

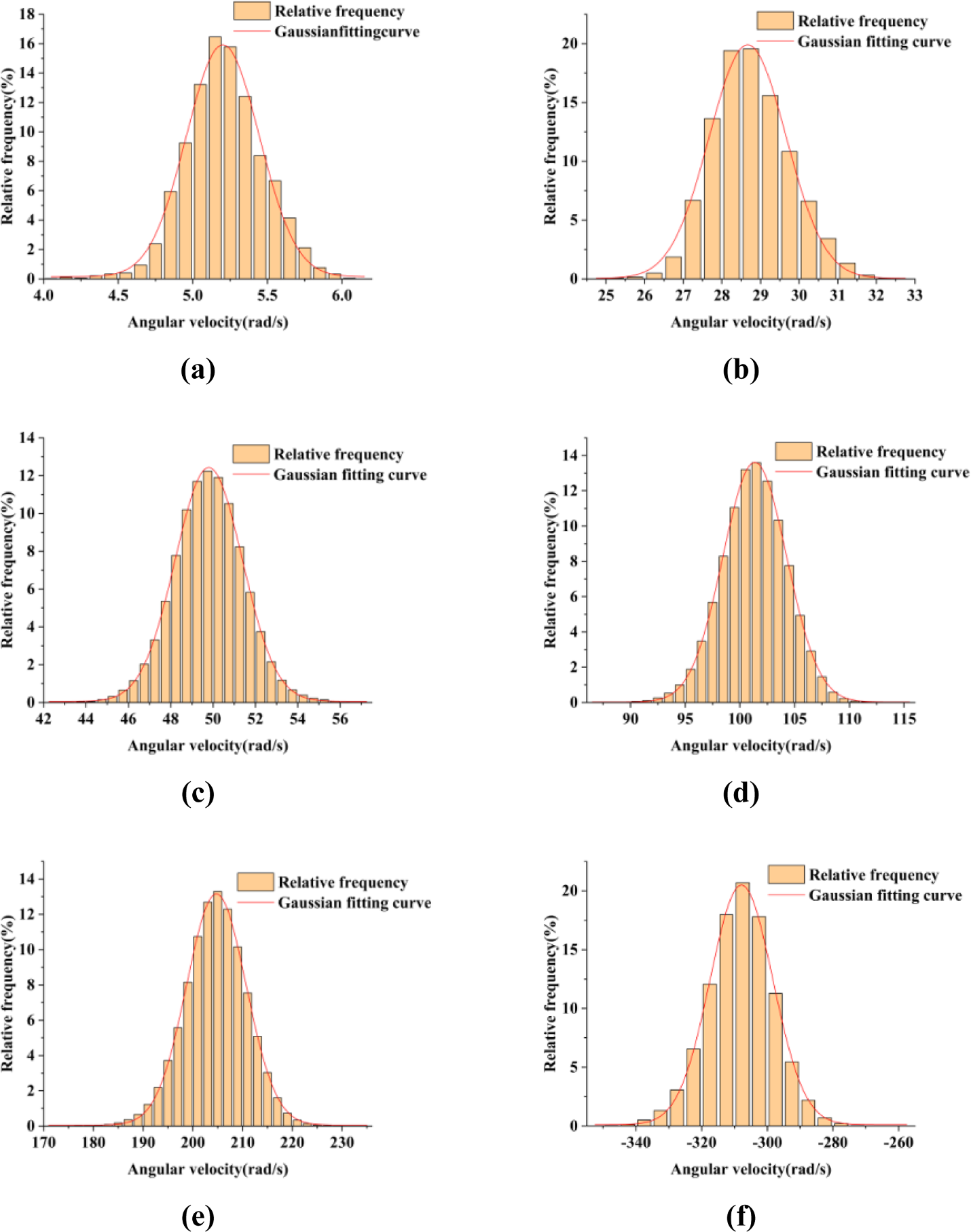
由于(2-2)仅适用于稳定阶段，因此分析了稳定阶段的仿真结果。结果如图4所示。稳定阶段角速度的分布特性在一定程度上呈现正态性。因此，杯式转子在稳定阶段的角速度可大致用正态分布模型拟合。该正态分布模型的函数表达式见(2-6)，其中μ为样本平均角速度，σ为样本标准差。

$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) \quad (2-6)
$$

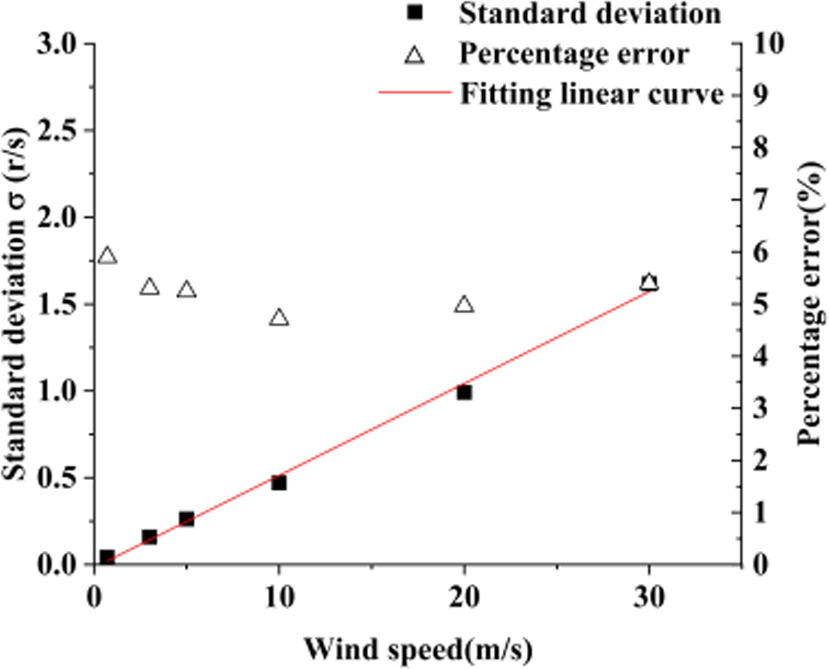
正态分布模型的均值和标准差随风速变化。仿真结果显示，在0.7 m/s至30 m/s范围内，标准差与风速几乎呈线性关系，如图5所示。相对误差稳定在约5.5%。因此，可获得不同风速下正态分布模型的参数。

将正态分布模型引入风速计系统后，若风速计中具备适当的信号检测结构和检测机制，则可显著降低风速计的功耗。因此，有必要对传统杯式风速计的信号检测结构和检测机制进行研究。

3. 设计

3.1. 信号检测结构与电路

通常，杯式风速计中有一个圆盘，其轴与风杯转子的轴相连，因此二者具有相同的角速度。杯式风速计通常使用光电门或霍尔元件来检测圆盘的旋转。由于霍尔元件的工作性能会受到温度影响，磁式杯式风速计通常需要添加温度补偿电路以减轻这种影响[23,24]，但这无法降低风速计的功耗。因此，本文选用光电式杯式风速计进行讨论。通常在圆盘边缘均匀分布有18个遮挡片[18,19]，当圆盘随风杯转子旋转时，光电门将输出脉冲信号，脉冲信号的频率可反映风杯转子的角速度。

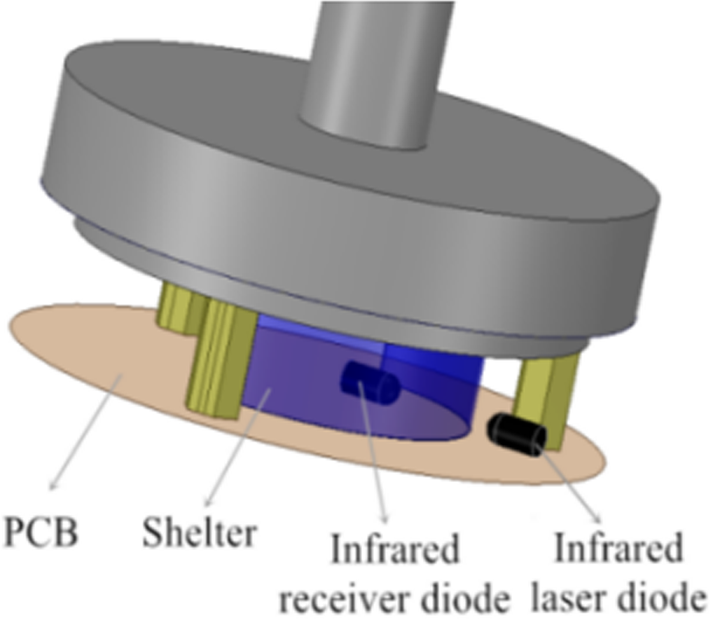
然而，这种信号检测结构不适合引入正态分布模型。由于圆盘上有大量遮挡片，很难将一个遮挡片与其他遮挡片区分开来。因此，杯式风速计的信号检测结构必须重新设计。在本工作中，对传统的杯式风速计信号检测结构进行了改进。改进后的信号检测结构中仅有一个遮挡片，占据圆盘边缘的一半位置，并且将光电门替换为红外激光二极管和红外接收二极管。所提出的杯式风速计的主结构显示在图6。

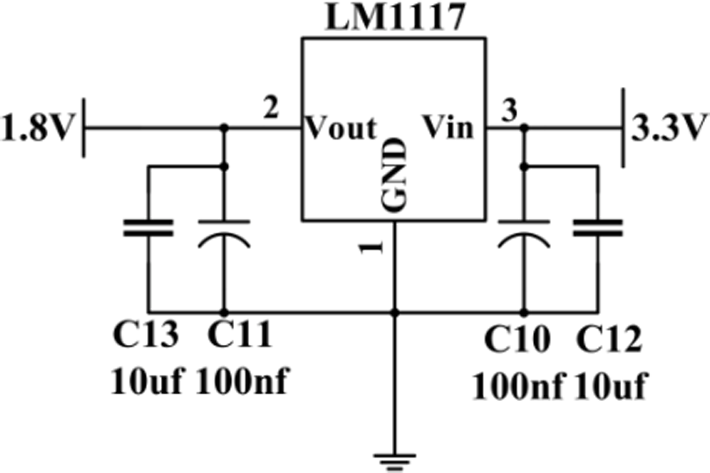
风速计系统由电源单元、微处理器、光发射器和光接收器组成。电源单元为电路供电，电源单元的电路如图7所示。采用基于高性能 ARM Cortex‐M4 32位RISC核的超低功耗微控制器STM32L476作为核心处理器，可大幅降低系统功耗。提出的杯式风速计检测到的数据将通过USART传输。

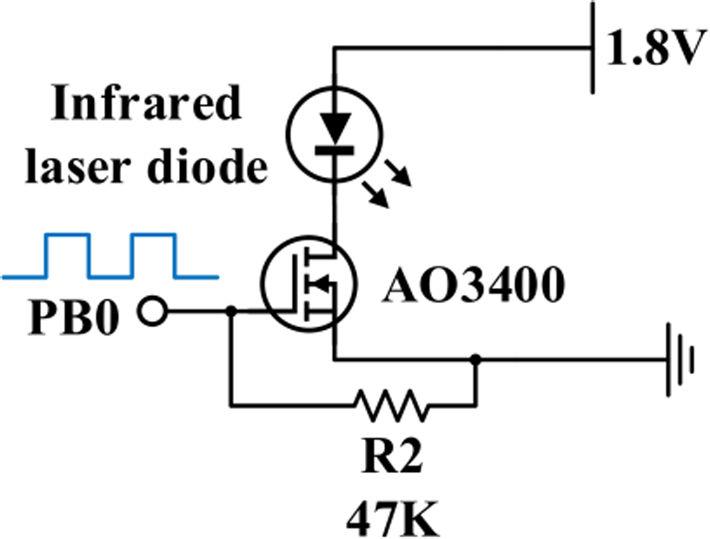
光发射器由红外激光二极管和MOSFET组成。由微处理器驱动的MOSFET用于开关激光二极管，通过在必要时关闭激光二极管以降低其功耗。此外，微处理器将生成脉冲信号以在期间驱动激光二极管的工作时间。此后，激光二极管工作时也可以节省功率。光发射器的电路如图8所示。

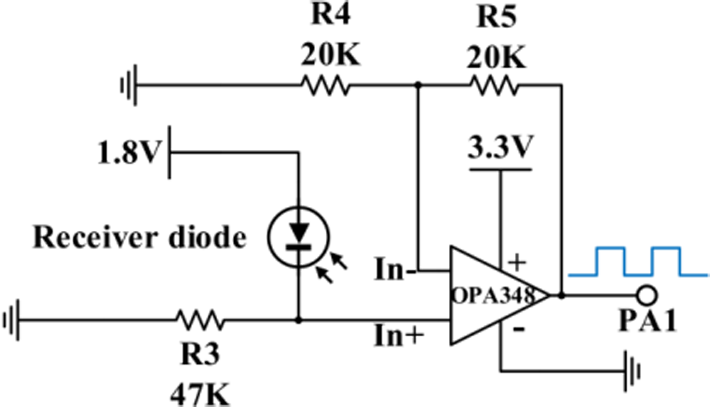
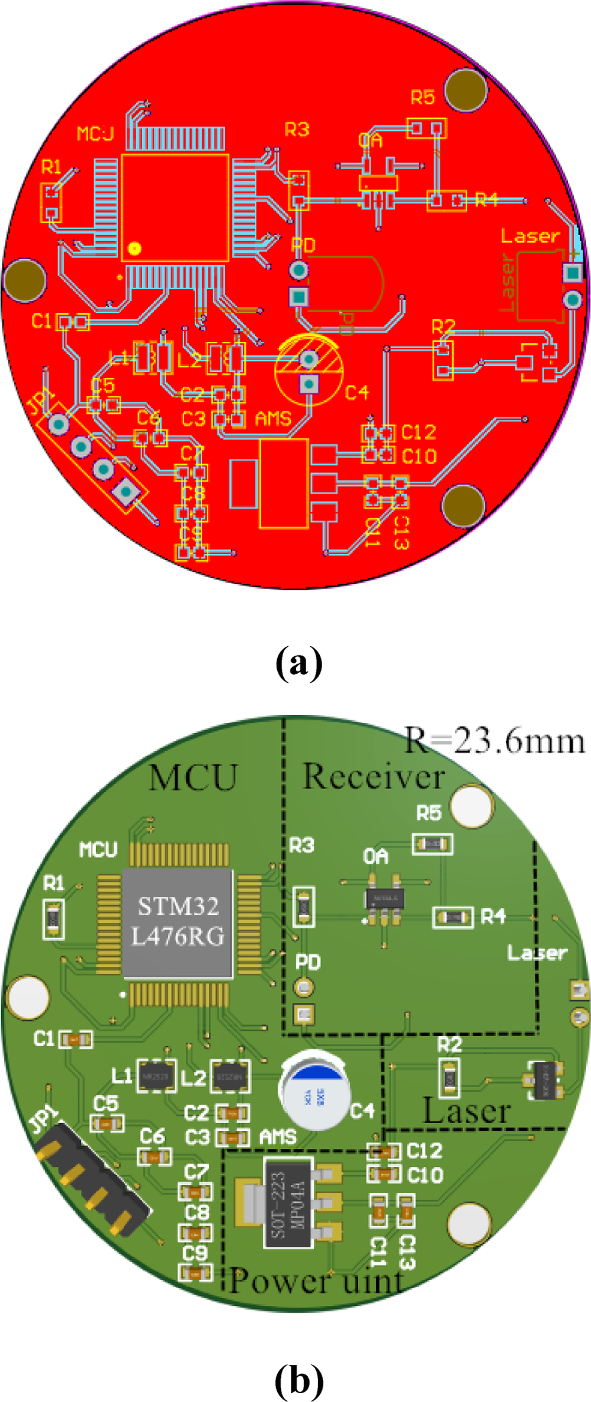
光接收器由红外接收二极管和运算放大器组成。当接收到红外信号时，接收二极管会输出与红外光强度相对应的高电压。通过检测该电压，微处理器可以判断发射器与接收器之间是否存在遮挡。高电压表示无遮挡，而低电压则表示存在遮挡。由于光源中的激光二极管是根据微处理器发送的脉冲信号工作的，其发出的红外光强度低于正常水平。因此，红外接收二极管的输出电压将低于微处理器可识别的高电压阈值，需要对该电压进行放大。因此，采用运算放大器电路以确保红外接收二极管输出的高低电压能够被正确识别。图9显示了光接收器的电路，图10显示了提出的杯式风速计的印刷电路板布局。

3.2. 低功耗风速检测方法

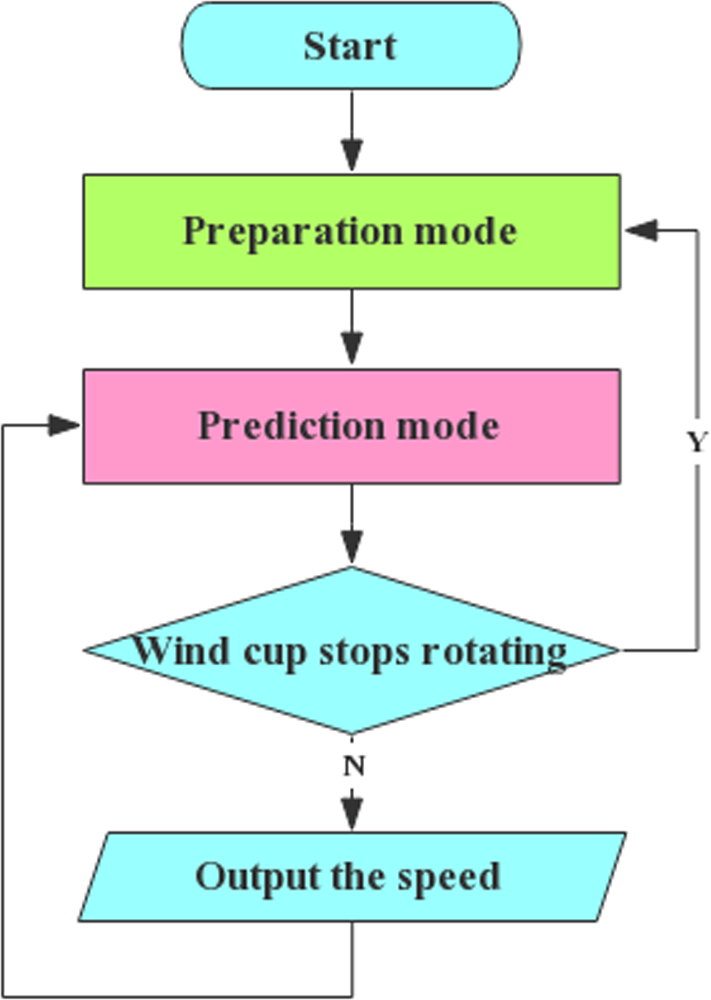
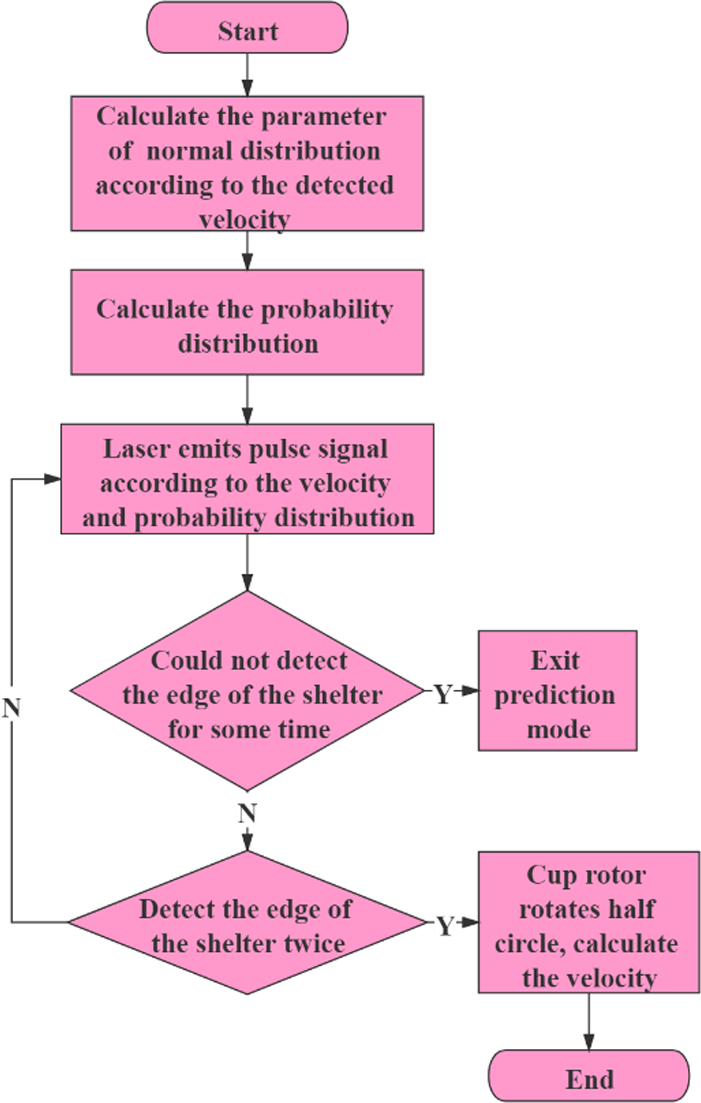
为提出的杯式风速计设计了两种工作模式，即准备模式和预测模式。如图11所示，风速计首先在准备模式下工作。它将检测风杯转子的角速度，以获取当前正态分布模型的参数。利用这些参数，风速计可以转入预测模式。除非风速低于启动风速，否则风速计将继续在预测模式下工作。

风速计的准备模式应具有低功耗特性。当风杯转子停止时，若风速计继续进行检测，将会浪费大量电能。考虑到风速计在预测模式下工作时能够修正准备模式中的检测误差，因此可通过降低准备模式的检测精度来减少其功耗。

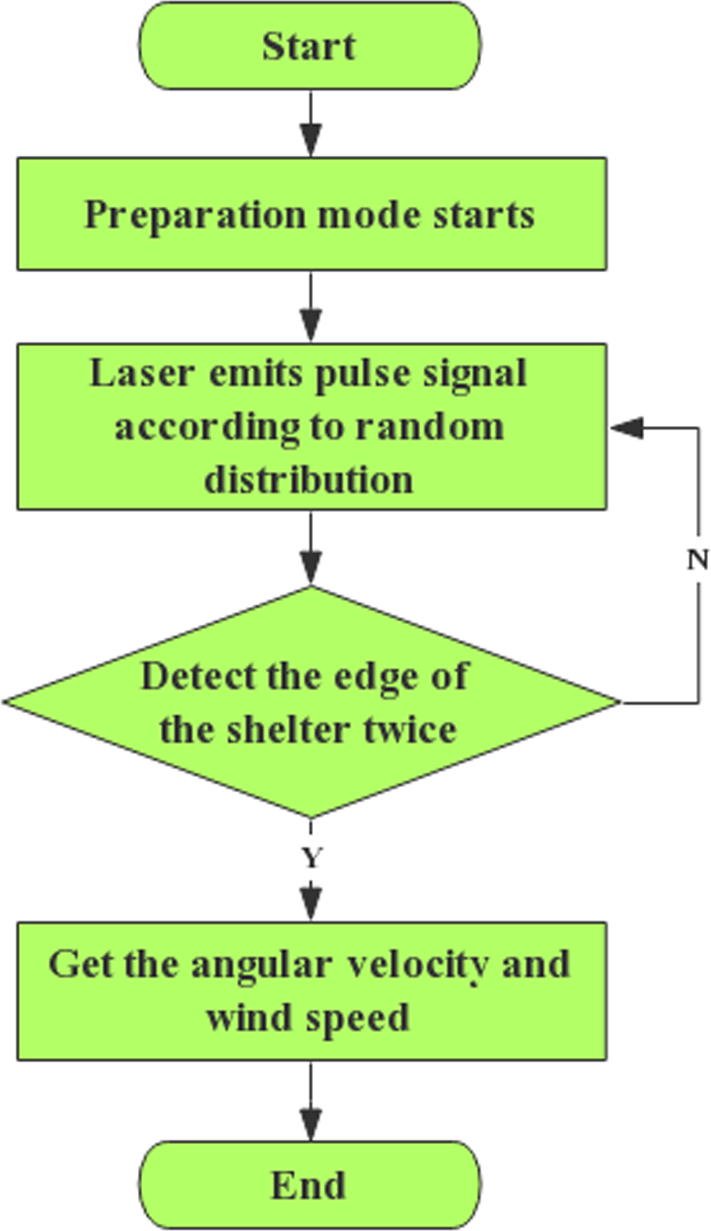
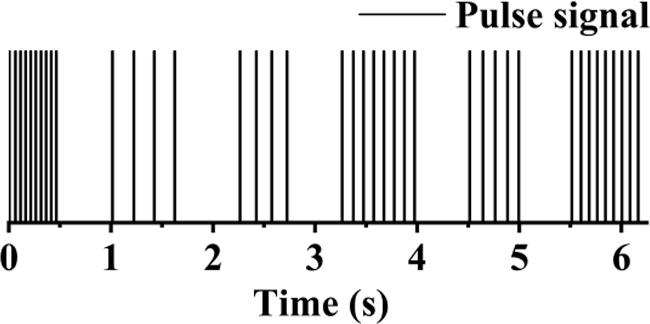
因此，发射器被设计为间歇工作，当检测到遮挡物的两个边沿时，所需时间是原来的两倍，以便能够计算杯式风速计的转速。如果发射器的工作时间等于其间隔时间，例如以1秒工作、1秒间隔运行，则该间隔必须足够长，否则当杯式风速计以某一速度旋转时，可能无法检测到遮挡物。因此，在准备模式下，发射器的工作时间和间隔应为随机而非固定，以确保不会遗漏杯式风速计的任何运动。此外，发射器在每次工作间隔内发出的脉冲信号频率也应具有随机性，以有助于提高准备模式下的精度。

综上所述，在准备模式下保证低功耗的前提下，理想情况下发射器应输出持续时间不等、且以随机、不等间隔发出的脉冲信号。算法流程图如图12所示，脉冲信号分布的示意图如图13所示。

预测模式作为风速计的主要工作模式，基于在此模式下每次检测均在旋转稳定阶段进行的假设。在该模式下，利用测量得到的角速度和正态分布模型，可以预测下一次检测时可能的角速度及其概率。随后，可预测挡板边缘被检测到的可能时间。激光器将在可能的时间发射脉冲信号以检测挡板边缘。脉冲信号频率将随概率和测量得到的角速度而变化。预测模式的算法流程如图14所示。

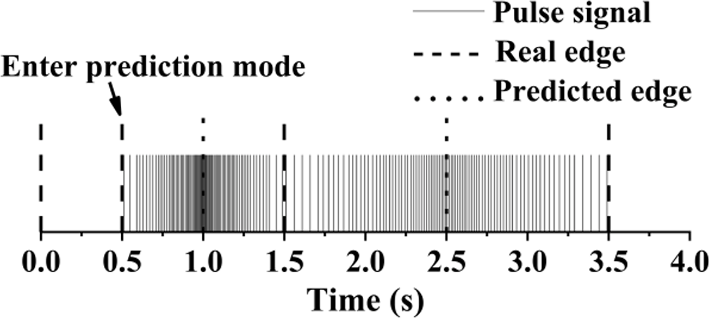
在风速计内部，只有一个遮挡物占据其圆盘边缘的一半。并且，当检测到挡板的一个边缘时，另一个边缘的位置已知，这是先决条件。当风速计在准备模式下刚刚完成测量并进入预测模式时，风速计的速度和挡板边缘位置是已知的。风速计将转速转换为风速，并且如图5所示，可以获得正态分布的标准差。正态分布的均值取自测得的转速，因此可根据正态分布模型获得风速计速度在下一次检测时的时间置信区间。由于挡板另一边缘的位置以及风速计速度的置信区间已知，因此可将该置信区间转换为时间置信区间，在此期间，风速计可通过根据角速度的概率分布发射不同频率的脉冲，在相应时间检测挡板边缘。如果风速恒定，发射器可以在时间置信区间内发射信号脉冲以检测挡板边缘并获取转速。

利用测得的速度，风速计将更新正态分布的参数和置信区间，并继续执行上述过程。由于风速不可能始终保持恒定，若超出置信区间，风速计仍应根据风速的概率分布运行。这使得风速计能够检测转速的突变，从而使检测算法具有相对的适应性。预测模式下脉冲信号分布的示意图如图15所示。

4. 实验

为了测试风速计的性能，设计了一个实验平台。如图16所示，该平台由一个风扇和一个简单的风洞组成。风洞包括一个收缩段和一个工作段。收缩段的长度为0.6米，工作段的长度为1.5米。风扇吹出恒定体积气流。气流速度随着体积的增加而增加。工作段内的风场相对稳定。平台中的风由商用热膜风速计 SMART SENSOR AR866A检测，该仪器测量范围为0.3米/秒至30米/秒（±5%）。杯轮旋转由商用光电转速计 UIN‐T UT372检测，该仪器测量角速度范围为0至99,999 RPM（±0.04%+ 2）。本文中，AR866A和UT372检测的数据被视为标准值。工作段的风速变化范围为0米/秒至10米/秒。

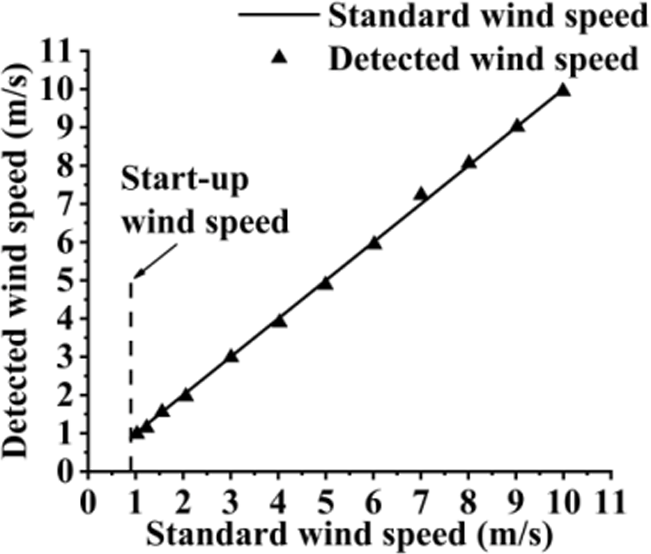
风速计的实测启动风速约为0.9米/秒，这意味着当风速小于0.9米/秒时，由于风杯转子轴上的摩擦，风杯转子无法完成完整旋转。

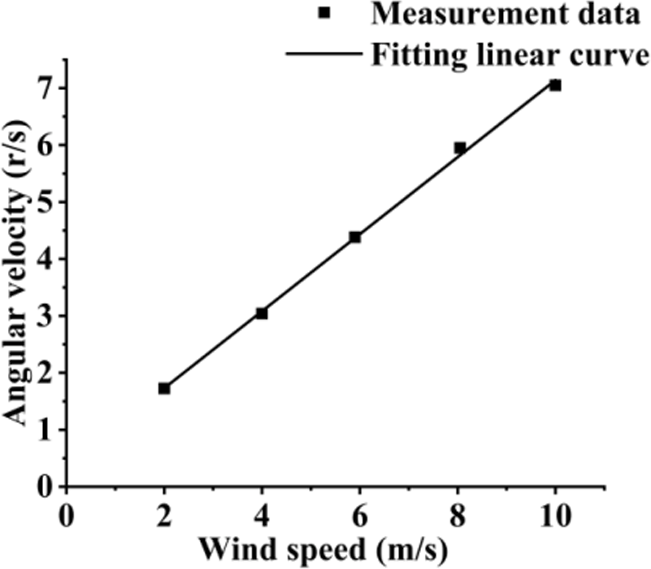
在0米/秒至10米/秒范围内以2 m/s 间隔检测风杯转子的角速度，得到角速度与风速之间的线性函数关系，结果如图17所示。测量角速度时，杯轮旋转处于稳定状态，每个点的值为100组采样数据的均值。采用最小二乘法对结果进行拟合，R² = 0.99，表明函数与结果拟合良好。该函数见于(3-1)，其中y表示杯式转子的角速度，x表示风速。

$$
y = 0.6823x + 0.3224 \quad (3-1)
$$

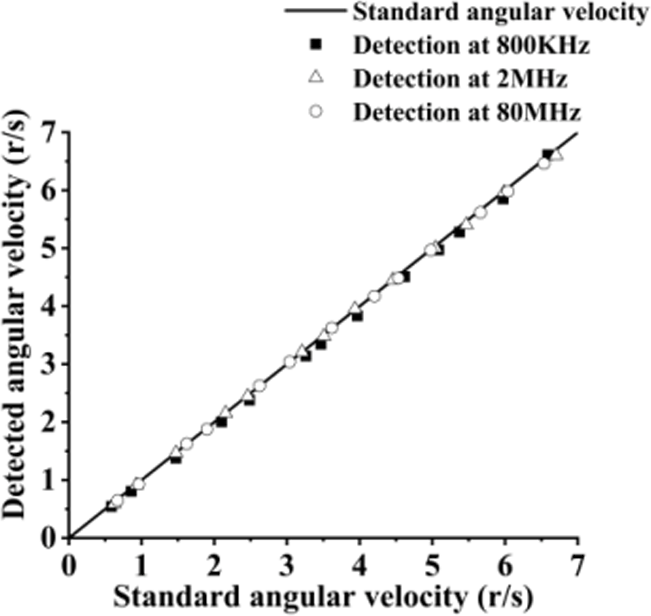
微控制器的系统频率会影响预测模式下角速度检测的精度。为了分析角速度检测精度与MCU时钟频率之间的关系，在约0.5r/s间隔、转速范围为1r/s至7r/s的条件下，对提出的杯式风速计在800 kHz（风速计系统的最低频率）、2 MHz和80 MHz（MCU的最大系统频率）三种系统时钟下进行了测试。在每个测试点，记录提出的杯式风速计在2分钟内检测到的角速度，各点的数值为样本数据的均值。检测结果如图18所示。

随着系统频率的降低，检测精度轻微下降。考虑到微控制器的功耗与系统频率正相关，因此800‐kHz是实现低功耗性能的首选系统频率。后续实验均采用800‐kHz的MCU系统时钟进行。

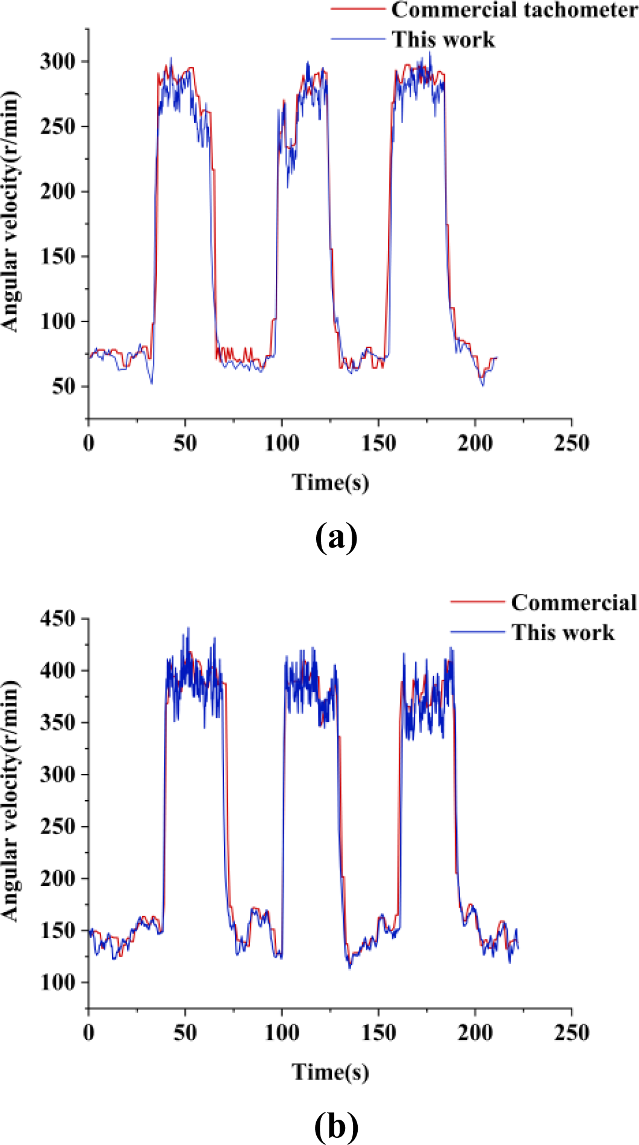
尽管风速计准确检测转速的能力已得到保证，但仍需测试风速计对风速突变的响应，以验证算法的自适应性。首先，将风速计置于恒定风场中使其稳定。然后风场将以周期性方式发生变化，从而可以观察风速计的响应。在整个过程中，使用商用光电转速计UT‐372监测杯式风速计的运动。测试结果如图19所示，证实了该风速计能够及时响应风速的变化。

风速计的性能通过风速进行测试，风速范围为1米/秒至10米/秒，间隔为1米/秒。为了测试风速计在极低风速下的性能，还进行了更多实验，风速范围为1米/秒至2米/秒。记录了超过4000的样本数据，检测结果如图20所示。每个点的值均为样本数据的均值。在1米/秒至10米/秒范围内，提出的杯式风速计与商用风速计相比，检测误差小于0.25米/秒。

风速计从准备模式切换到预测模式时，需要一定时间来响应实时风速。为了获得切换时间，将风速计在不同风场下进行测试，使其首先工作在准备模式，然后转入预测模式。结果如图21所示。当风速低于9米/秒时，风速计的切换时间小于1.1秒，在风速为9米/秒时测得的最小切换时间低于0.35秒。

此外，还进行了更多实验以测试提出的杯式风速计的响应时间。该风速计首先在0.9米/秒下以预测模式工作，然后风速会发生突然变化。结果表明，当提出的杯式风速计的风速增量小于9米/秒时，其响应时间小于1.2秒。切换时间与响应时间均与风速呈负相关。这是合理的，因为风杯转子的加速度随着风速增量的增加而增大。

图22显示了所提出的杯式风速计测得的功耗曲线。根据所提出的算法，微控制器生成的脉冲信号频率与风速呈正相关。因此，随着风速的增加，功耗略有上升。然而，在风速为10米/秒时，激光二极管测得的最大功耗仅为2.2毫瓦，仍比连续工作的激光二极管的功耗低75%。当风速低于10米/秒时，风速计的总功耗小于4.2毫瓦。表1展示了本工作采用所提出的信号检测算法及相应信号检测结构的杯式风速计与其他风速计（包括若干商用杯式风速计以及一些其他研究文献中设计的风速计）在性能上的对比。这证明了所提出的信号检测算法在降低风速计功耗方面具有更优的性能。

实验平台 (b) 平台中的风速计)

参考文献	Year	Type	检测范围	精度	功率	功耗
本工作	–	Cup	0–45 米/秒	±0.25 米/秒	4.2 毫瓦 在 10 m/s
PHWS‐5V‐V1	–	Cup	0–45 米/秒	±(0.3+0.03 V)米/秒	50 毫瓦
QS‐FS2	–	Cup	0–60 米/秒	±(0.3+0.03 V)米/秒	85 毫瓦
H. 施特姆[26]	2010	热式	0–60 米/秒	–	7.5 毫瓦
建峰 Wu[25]	2011	热式	1–25 米/秒	±4%	25 毫瓦
杨张[27]	2017	热式	0–2 米/秒	–	9.87 毫瓦
V. 斯托内利[28]	2017	热式	0–20 米/秒	±2% ±2 ◦	19.8 毫瓦
程玲 L[29]	2017	热式	0–2.54 米/s	–	402 毫瓦
Bo Sun[30]	2018	压力	5–60 米/秒	±4 %， ± 4 ◦	400 毫瓦
H B 风扇[3]	2018	超声波	0–20 米/秒	±3%	840 毫瓦
陈旭科[31]	2019	热式	0–20 米/秒	–	396 毫瓦
郭珍 Li[32]	2019	热式	0–20 米/秒	± 1%, 3 ◦	400–500 毫瓦

(1) 1 是本文模型选用的商用杯式风速计。(2) 2 是一种商用霍尔单脉冲杯式风速计。

5. 结论

本文提出了一种针对三杯风速计的自适应低功耗检测算法的设计。该检测算法的设计应用了CFD分析中发现的风杯转子旋转特性，同时对风速计的信号检测结构进行了改进以匹配该算法。通过对风速范围从0米/秒至10米/秒的测试验证了风速计的性能。实验结果表明，该风速计的启动风速为0.9米/秒，平均检测误差为0.25米/秒，在风速为10米/秒时风速计的功耗低于4.2毫瓦。所提出的算法在降低三杯风速计的功耗方面具有实际意义。

6. 资金来源格式

本工作部分受到国家自然科学基金项目编号61904206、广东省基础与应用基础研究基金项目编号2019A1515010002以及山东省重点研发计划（项目编号2018GHY115045）的资助。