L1神经网络与深度学习-2.4梯度下降法

原创 已于 2025-10-15 14:51:30 修改 · 922 阅读 · 6 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#深度学习 #神经网络 #人工智能

于 2025-10-15 14:13:49 首次发布

以刚才讲过的logistic回归为例，我们的目标是要找到 使得J(w,b)尽可能小 的w和b

如上图所示,水平的两个轴是w和b【为了方便绘图认为w是一个实数，实际上是更高维的】,J(w,b)是一个曲面。曲面在某个点(w,b)的高度，就是J(w,b)的值
我们要找到w和b使得成本函数J的值为最小值

J是一个凸函数，对于凸函数，在哪里初始化都会到达或接近最低点

而下面这种函数会存在很多局部最优解

梯度下降法：

从初始点开始，朝着最陡的下坡方向走一步，这是一次迭代；随着迭代，很有希望收敛到或接近局部最优解

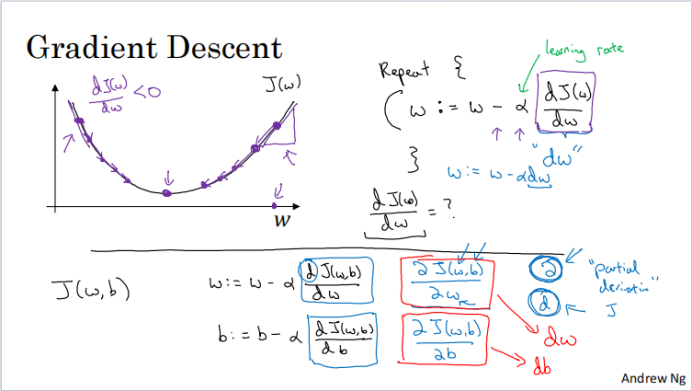
上图是忽略b，用J与w的关系曲线来演示梯度下降法，这样图象是二维的，便于理解

Repeat\{ w:=w-\alpha \frac{dJ(w)}{dw} \}

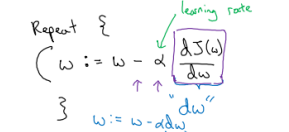
“:=”表示更新，“repeat”就是重复更新w的值

α是学习率，可以控制每一次迭代的步长。

\frac{dJ(w)}{dw}是导数

无论初始点在左边还是右边，最终都会收敛到中间的最低点
同理，对于有两个参数的J（w,b）,迭代过程为：

w:=w-\alpha \frac{\partial J(w,b)}{\partial w}

b:=b-\alpha \frac{\partial J(w,b)}{\partial b}

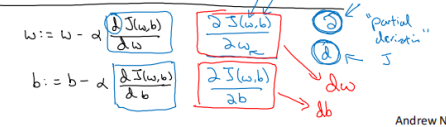
\partial为偏导数符号，因为J（w,b）有两个变量。不过在编写代码时都会写为dw和db

深度学习知识点全面总结
专注大数据与人工智能技术分享，欢迎私信加群互相学习！
01-05 37万+
本文详细介绍深度学习概念及原理，参考网上相关资料汇总，内容包含众多章节，包括神经网络基础及常见深度学习网络结构介绍，用于个人学习总结，适合深度学习初学者学习。同时介绍机器学习常见的分类算法：SVM、神经网络、随机森林、逻辑回归、KNN、贝叶斯。常见的监督学习算法：感知机、SVM、人工神经网络、决策树、逻辑回归.........
L1神经网络与深度学习-2.9&2.10logistic回归中的梯度下降法
mcqly的博客
10-16 554
(超爽中英!) 2024公认最好的【吴恩达深度学习】教程！附课件代码 Professionalization of Deep Learning。
神经网络系列---常用梯度下降算法
weixin_43763292的博客
02-24 2746
常用梯度下降算法 当涉及不同的梯度下降算法时，每种算法都有其独特的特点和优化策略。下面对每种算法进行详细解释： 随机梯度下降（Stochastic Gradient Descent，SGD）： 算法原理：在每次迭代中，随机选择一个训练样本来计算损失函数的梯度，并更新模型的参数。由于随机选择样本，梯度估计存在一定的噪声，导致优化路径不稳定，但收敛速度较快。 优点：收敛速度快，计算开销较小。 缺点：优化路径不稳定，可能会震荡，难以找到全局最优解。 算法原理：在每次迭代中，使用所有训练样本来计算损
神经网络与深度学习--网络优化与正则化
weixin_46034279的博客
05-01 3070
神经网络调参是深度学习中不可或缺的一环，它直接影响着模型的性能和泛化能力。当前神经网络模型应用到机器学习时仍有一些问题，主要包括两大类。优化问题深度神经网络优化十分困难。首先他的损失函数是一个非凸函数，找到局部最优解容易，但找到全局最优解并非容易。其次，神经网络参数非常多，训练数据很大，所以无法使用计算代价很高的二阶优化方法。最后，神经网络存在梯度消失或爆炸问题。泛化问题由于神经网络复杂度很高，拟合能力很强，很容易在训练集上过拟合。因此要考虑一定的正则化方法来改进网络泛化能力。
神经网络与深度学习-课后习题
using namespace 数学工具构造器;
02-22 3811
文章目录2 机器学习概述习题2-1 分析为什么平方损失函数不适用于分类问题．习题2-2 线性回归的权重习题2-3 XXTXX^TXXT的秩2-4 结构风险最小化 最小二乘估计 岭回归2-5 最大似然估计与最小二乘估计在标签服从高斯分布时等价2.6 最大似然估计与最大后验估计2.9 欠拟合→高偏差，过拟合→高方差2.11 N-gram3 线性模型多分类Logistic RegressionSoftmax Regression感知机支持向量机y⋅y^y\cdot \hat{y}y⋅y^​ 形式的损失函数LR S
深度学习02-神经网络(MLP多层感知器)
热门推荐
liaomin416100569的专栏
05-09 9万+
神经网络是一种基于生物神经系统结构和功能特点而设计的人工神经网络模型，具有很强的自适应性和非线性映射能力。神经网络由多个神经元（或称节点）组成，这些神经元通过连接权重相互连接，构成多层的网络结构。每个神经元接收到来自其它神经元的信号，并将这些信号加权线性组合后通过激活函数进行非线性转换，最终输出给下一层神经元或输出层。学习机器学习后，学习神经网络可以帮助你更深入地理解模式识别和人工智能领域的基础知识。神经网络在很多领域都有广泛的应用，例如计算机视觉、自然语言处理、语音识别等。
机器学习与深度学习15-神经网络
beijieweiyu的博客
06-09 1484
神经网络（Neural Network）是一种机器学习算法，模仿人脑的神经系统结构和工作原理。它由多个称为神经元的节点（或单元）组成，这些节点通过连接（权重）相互传递信息，并在输入数据上执行复杂的非线性计算，基本原理为输入层（Input Layer）接收外部输入数据，并将其传递给下一层隐藏层（Hidden Layer）是位于输入层和输出层之间的一系列层，负责处理和转换输入数据输出层（Output Layer）产生最终的结果或预测每个连接都有一个相关的权重，用于调整输入值的重要性。
神经网络与深度学习
weixin_69884785的博客
09-10 1086
一.神经网络 1.单层神经网络 2.多层神经网络 3.卷积神经网络（CNNs） 卷积的操作原理： 滤波器权重： 检验器层： 池化层： 卷积神经网络架构： 数据增强： 4.文档分类 5.循环神经网络（RNN） RNN： RNN的计算过程： 回归问题的损失函数： RNN的应用实例： 二.神经网络的拟合过程 1.梯度下降 2.随机梯度下降 三.深度学习 四.双下降
深度学习---（1）神经网络与多层感知机
qq_51749909的博客
10-22 1782
卷积神经网络（Convolutional Neural Network，简称CNN）是一种深度学习模型，特别适合处理图像和视频等数据。它通过模拟生物视觉皮层的工作方式，能够有效提取图像中的特征。
神经网络深度学习-2020最新资料.rar
06-24
综上所述，这份《神经网络深度学习-2020最新资料》包含的内容广泛且深入，涵盖了深度学习的多个核心主题，对于想深入了解和学习深度学习的读者来说是一份宝贵的资源。通过阅读其中的"Neural Network and Deep ...
精选资源
【深度学习-吴恩达】L1-3 浅层神经网络 作业
07-29
在这个"【深度学习-吴恩达】L1-3 浅层神经网络 作业"中，我们将关注三个核心概念：神经网络的基础、前向传播以及反向传播算法。 首先，神经网络是一种模仿人脑神经元结构的计算模型，由大量的节点（称为神经元）和...
神经网络深度学习-2020最新资料+数学.rar
06-24
4. 网络优化与正则化：深度学习中的优化通常采用梯度下降法，如随机梯度下降（SGD）及其变种。正则化是防止过拟合的技术，包括L1和L2正则化、dropout等。 5. 记忆与注意力机制：在RNN和Transformer等模型中，注意力...
神经网络与深度学习.rar
09-26
《神经网络与深度学习》是一本深度学习领域的经典著作，主要涵盖了神经网络的基本概念、原理以及深度学习的应用。这本书在2019年4月10日完成，因其深入浅出的讲解方式，成为了初学者入门的首选教材。深度学习是人工...
【文献阅读】DP-Site：一种基于双重深度学习的蛋白质-肽相互作用位点预测方法
weixin_42038527的博客
12-16 465
研究团队开发了一款名为DP-Site的AI工具，仅需分析蛋白质的氨基酸序列（“设计图”），就能精准锁定小分子药物的潜在“靶点”。DP-Site的核心创新在于其 “双专家会诊”模式。一位是“图像专家”，擅长分析序列的局部结构特征；另一位是“语义专家”，擅长理解序列的全局上下文信息。两者协同工作，使其预测综合性能（F1分数）达到0.661，超越此前所有方法。
【CNN与卷积神经网络（吴恩达）】卷积神经网络学习笔记
qq_62361050的博客
12-12 1023
池化层类似卷积运算，在这里举一个最大池化的例子，即在一个4x4的图像中采用一个2x2的核，这个《核》只是对对应区域进行取最大值计算，以步长为2进行移动计算，在每次计算中取区域中的最大值，这样就可以提取出图像中的最显著的特征。以下是对于三维卷积中一些尺寸数据的描述，和二维卷积相似，只不过在n x n后面新加了一个尺寸数据nc，这个nc即表示图像的通道数，剩余对于输出图像的尺寸的计算公式和二维卷积下的一模一样。这种卷积下的卷积核和二维卷积是一样的，只不过由于有三个图像矩阵，所以应该对应有三层卷积核，即。
基于深度学习的肾结石检测系统演示与介绍(YOLOv12/v11/v8/v5模型+Pyqt5界面+训练代码+数据集)
最新发布
ningfoshao8678的博客
12-16 679
本文介绍了基于YOLO目标检测算法开发的肾结石检测系统。该系统支持图片、视频、文件夹批量及摄像头实时检测，包含用户登录、多模型切换等功能。技术栈采用Python3.10、PyQt5和SQLite，对比了YOLOv5/v8/v11/v12四种模型性能，其中YOLO12n精度最高(mAP40.6%)，YOLO11n速度最快(56.1ms)。系统在17000张肾脏影像数据集上训练，mAP@0.5达90%，F1值0.86，能有效识别肾结石位置并显示置信度。
深度学习中 z-score 标准化理解
musk1212的博客
12-11 1130
摘要： z-score标准化是深度学习中关键的数据预处理方法，通过将数据转换为均值为0、标准差为1的分布，有效提升模型训练效率并消除特征量纲差异。其核心公式为z=(x-μ)/σ，适用于加速收敛、平衡多特征权重及异常值检测等场景。与Min-Max归一化相比，z-score对异常值更鲁棒，是神经网络训练的首选方法。需注意避免数据泄露问题（测试集必须使用训练集的μ和σ），并处理标准差为0的特殊情况。批量归一化(BatchNorm)是z-score的动态扩展版本。
深度学习理论与实战：反向传播、参数初始化与优化算法全解析
2501_92613722的博客
12-16 658
深度学习训练核心闭环：精准算梯度、合理初始化参数、高效更参数 反向传播：链式求导为基，从损失反向回溯算梯度，附 Sigmoid 实例 参数初始化：讲手动 / 经典方法，Module 初始化技巧与核心原则、选择 优化算法：SGD 为基，动量法 / Adagrad/RMSProp/Adadelta/Adam 解析与对比 核心总结：反向传播、初始化、优化算法要点及训练细节
RNN（循环神经网络）原理
weixin_45776000的博客
12-12 490
RNN的突破：引入"记忆"概念，让网络可以记住之前的信息来处理当前输入。无法建模时间依赖：比如语言中"我今天吃了__"的预测需要前面信息。无记忆性：每个输入独立处理，忽略序列中元素的时间/顺序关系。关键：所有时间步共享相同的权重参数 W, U, V。主要问题：梯度消失/爆炸，通过LSTM/GRU缓解。W: 隐藏状态权重 (h_t-1 → h_t)应用场景：NLP、时间序列、语音识别等序列任务。输入：序列 → 编码 → 解码 → 输出序列。U: 输入权重 (x_t → h_t)
梯度下降法在机器学习与神经网络中的应用
在神经网络的训练中，梯度下降法通常与反向传播算法结合使用。反向传播算法可以高效地计算损失函数相对于网络中每个权重的梯度。然后，梯度下降法利用这些梯度来更新权重，以降低输出与目标之间的差异。 梯度下降法...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值