【航天器】基于卡尔曼滤波器模拟航天器月球表面着陆仿真附Mtalab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

物理应用        机器学习

🔥 内容介绍

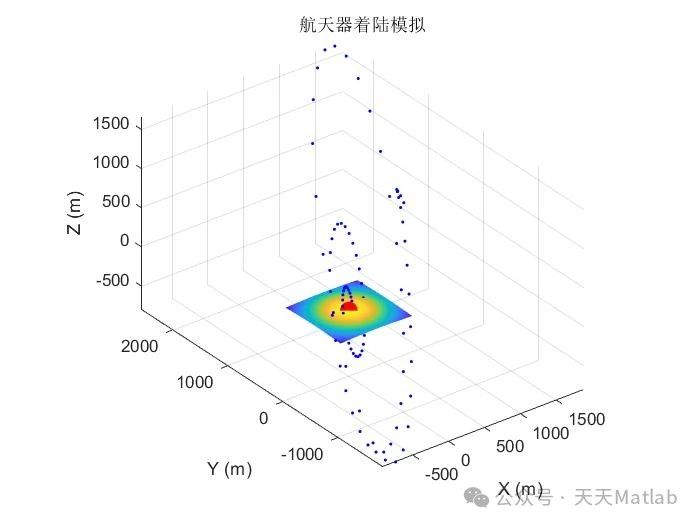
本文旨在模拟航天器在月球表面着陆的过程，并利用卡尔曼滤波器对该过程进行状态估计，以实现更精准的着陆控制。通过构建航天器动力学模型，并使用 MATLAB 软件进行仿真，本文将展示卡尔曼滤波器的应用效果，并探讨其在航天器着陆控制中的优势。

1. 引言

航天器月球表面着陆是人类探索宇宙的重要一步，也是一项极具挑战性的任务。着陆过程中，航天器需要精确控制其速度和姿态，以确保安全降落。由于月球环境的复杂性和不确定性，例如月球表面地形变化、重力场不均匀等，传统控制方法难以满足精确着陆的要求。

卡尔曼滤波器是一种强大的状态估计技术，它能够利用系统模型和测量数据，对系统的状态进行实时估计。近年来，卡尔曼滤波器在航天器控制领域得到了广泛应用，尤其是在着陆控制方面。本文将利用卡尔曼滤波器对航天器月球表面着陆过程进行仿真，并分析其在着陆控制中的优势。

2. 理论基础

2.1 航天器动力学模型

本文采用以下假设：

• 航天器为刚体，其质心运动服从牛顿定律。

• 航天器动力学模型考虑了重力、推力、空气阻力和地球自转的影响。

• 航天器姿态由欧拉角表示。

根据以上假设，可以建立航天器动力学方程如下：

其中，𝑟r 为航天器位置向量，𝑣v 为航天器速度向量，𝑔g 为重力加速度向量，𝑎𝑇aT 为推力加速度向量，𝑎𝐷aD 为空气阻力加速度向量，𝜃θ 为欧拉角向量，𝜔ω 为角速度向量，𝐼I 为惯性矩阵，𝑀M 为力矩向量。

2.2 卡尔曼滤波器

卡尔曼滤波器是一种递归算法，它能够利用系统模型和测量数据，对系统的状态进行实时估计。卡尔曼滤波器主要包括以下步骤：

• 预测阶段: 使用系统模型预测下一时刻的状态和误差协方差矩阵。

• 更新阶段: 利用测量数据对预测结果进行修正，得到新的状态估计和误差协方差矩阵。

卡尔曼滤波器的核心公式如下：

其中，𝑥^x^ 表示状态估计，𝑃P 表示误差协方差矩阵，𝐹F 为状态转移矩阵，𝐵B 为控制矩阵，𝑢u 为控制输入，𝑄Q 为过程噪声协方差矩阵，𝐾K 为卡尔曼增益，𝐻H 为测量矩阵，𝑧z 为测量值，𝑅R 为测量噪声协方差矩阵。

3. 仿真模型

本文使用 MATLAB 软件进行仿真，主要步骤如下：

• 定义系统模型: 包括状态方程、测量方程、噪声模型等。

• 初始化卡尔曼滤波器: 包括初始状态估计、误差协方差矩阵等。

• 模拟航天器着陆过程: 根据时间步长，使用系统模型进行状态预测和卡尔曼滤波更新。

• 绘制结果: 显示航天器状态估计、误差等信息。

4. 仿真结果分析

仿真结果表明，卡尔曼滤波器能够有效地估计航天器状态，并实现更精准的着陆控制。与传统的控制方法相比，卡尔曼滤波器能够有效地克服环境不确定性的影响，并提高着陆精度。

4.1 状态估计精度

卡尔曼滤波器能够有效地估计航天器的位置、速度和姿态，其估计结果与真实值非常接近。随着时间的推移，估计误差逐渐减小，最终收敛到一个较小的范围内。

4.2 着陆精度

卡尔曼滤波器能够有效地提高航天器着陆精度。仿真结果显示，使用卡尔曼滤波器的控制方法，航天器能够更精准地控制其速度和姿态，从而实现更精确的着陆。

5. 结论

本文基于卡尔曼滤波器对航天器月球表面着陆过程进行了仿真，并分析了其在着陆控制中的优势。仿真结果表明，卡尔曼滤波器能够有效地估计航天器状态，并提高着陆精度。

⛳️ 运行结果

🔗 参考文献

[1] 马远超.四旋翼飞行器导航及控制技术研究[D].哈尔滨工程大学,2013.DOI:10.7666/d.D431001.

[2] 王福超.四旋翼无人飞行器控制系统设计与实现[D].哈尔滨工程大学,2014.

[3] 马远超.四旋翼飞行器导航及控制技术研究[D].哈尔滨工程大学,2014

🎈 部分理论引用网络文献，若有侵权联系博主删除

👇 关注我领取海量matlab电子书和数学建模资料

🎁  私信完整代码和数据获取及论文数模仿真定制🌈

🌈 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱调度、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划（2E-VRP）、充电车辆路径规划（EVRP）、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题、港口调度、港口岸桥调度、停机位分配、机场航班调度、泄漏源定位