【智能优化算法】切诺贝利灾难优化器（CDO）附matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

🔥 内容介绍

智能优化算法一直是人工智能领域的热门话题，它们被广泛应用于各种领域，如工程优化、金融分析、物流规划等。在这些应用中，切诺贝利灾难优化器（CDO）是一种备受关注的智能优化算法。本文将介绍CDO算法的原理、特点以及在实际应用中的表现。

CDO算法是一种基于切诺贝利灾难的智能优化算法，它模拟了切诺贝利核事故中的灾难性事件，并通过优化算法来寻找最优解。该算法的核心思想是通过模拟灾难事件，找到最优的应对策略，从而得到最优解。CDO算法的优化过程可以被描述为一个动态的搜索过程，它不断地调整参数和策略，以适应不断变化的环境。

CDO算法具有以下几个特点：首先，它是一种自适应的优化算法，能够根据环境的变化自动调整参数和策略。其次，它具有较强的鲁棒性，能够应对各种复杂的优化问题。此外，CDO算法还具有较高的收敛速度和全局搜索能力，能够在较短的时间内找到较优解。

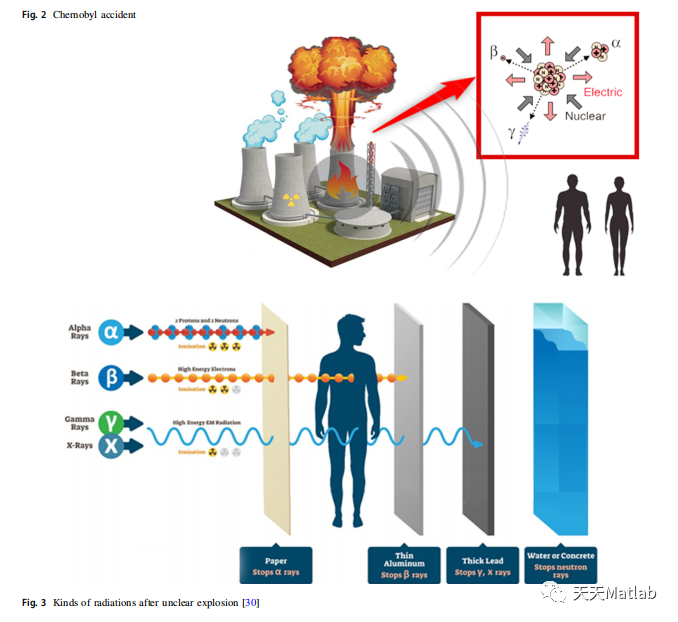
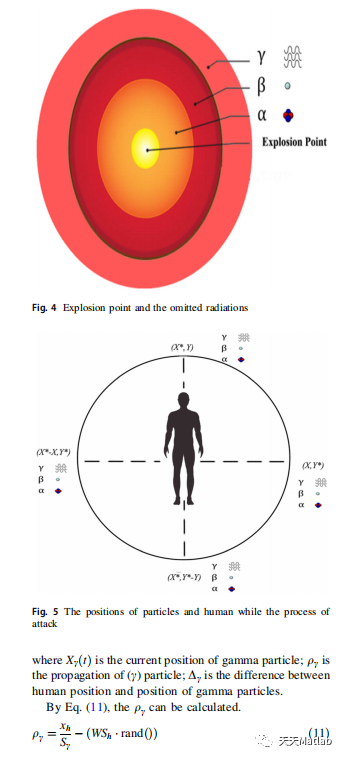
在实际应用中，CDO算法已经被广泛应用于各种领域。例如，在工程优化中，CDO算法可以用于优化复杂的结构设计，提高结构的稳定性和安全性。在金融分析领域，CDO算法可以用于优化投资组合，最大化收益并控制风险。在物流规划中，CDO算法可以用于优化配送路径，降低成本并提高效率。

总的来说，切诺贝利灾难优化器（CDO）是一种非常有潜力的智能优化算法，它具有较强的自适应性、鲁棒性和全局搜索能力，能够在各种复杂的优化问题中取得较好的效果。随着人工智能技术的不断发展，相信CDO算法将在更多领域展现出其强大的优化能力。

📣 部分代码

​% 画图程序​function func_plot(func_name)​[lb,ub,dim,fobj]=Get_Functions_details(func_name);​switch func_name     case 'F1'         x=-100:2:100; y=x; %[-100,100]            case 'F2'         x=-100:2:100; y=x; %[-10,10]            case 'F3'         x=-100:2:100; y=x; %[-100,100]            case 'F4'         x=-100:2:100; y=x; %[-100,100]    case 'F5'         x=-200:2:200; y=x; %[-5,5]    case 'F6'         x=-100:2:100; y=x; %[-100,100]    case 'F7'         x=-1:0.03:1;  y=x;  %[-1,1]    case 'F8'         x=-500:10:500;y=x; %[-500,500]    case 'F9'         x=-5:0.1:5;   y=x; %[-5,5]        case 'F10'         x=-20:0.5:20; y=x;%[-500,500]    case 'F11'         x=-500:10:500; y=x;%[-0.5,0.5]    case 'F12'         x=-10:0.1:10; y=x;%[-pi,pi]    case 'F13'         x=-5:0.08:5; y=x;%[-3,1]    case 'F14'         x=-100:2:100; y=x;%[-100,100]    case 'F15'         x=-5:0.1:5; y=x;%[-5,5]    case 'F16'         x=-1:0.01:1; y=x;%[-5,5]    case 'F17'         x=-5:0.1:5; y=x;%[-5,5]    case 'F18'         x=-5:0.06:5; y=x;%[-5,5]    case 'F19'         x=-5:0.1:5; y=x;%[-5,5]    case 'F20'         x=-5:0.1:5; y=x;%[-5,5]            case 'F21'         x=-5:0.1:5; y=x;%[-5,5]    case 'F22'         x=-5:0.1:5; y=x;%[-5,5]         case 'F23'         x=-5:0.1:5; y=x;%[-5,5]  end    ​    ​L=length(x);f=[];​for i=1:L    for j=1:L        if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0            f(i,j)=fobj([x(i),y(j)]);        end        if strcmp(func_name,'F15')==1            f(i,j)=fobj([x(i),y(j),0,0]);        end        if strcmp(func_name,'F19')==1            f(i,j)=fobj([x(i),y(j),0]);        end        if strcmp(func_name,'F20')==1            f(i,j)=fobj([x(i),y(j),0,0,0,0]);        end               if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1            f(i,j)=fobj([x(i),y(j),0,0]);        end              endend​surfc(x,y,f,'LineStyle','none');​end​​

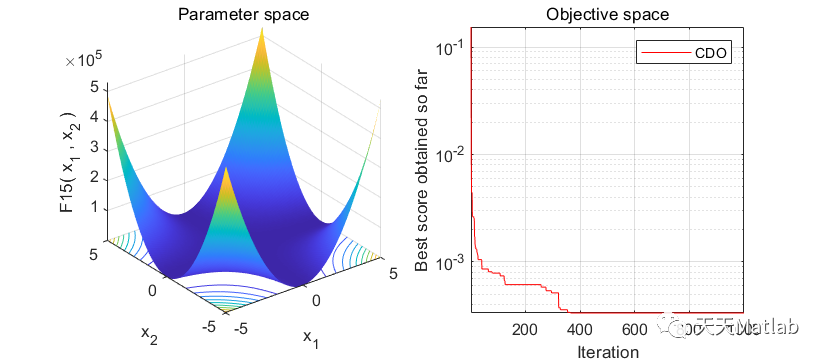
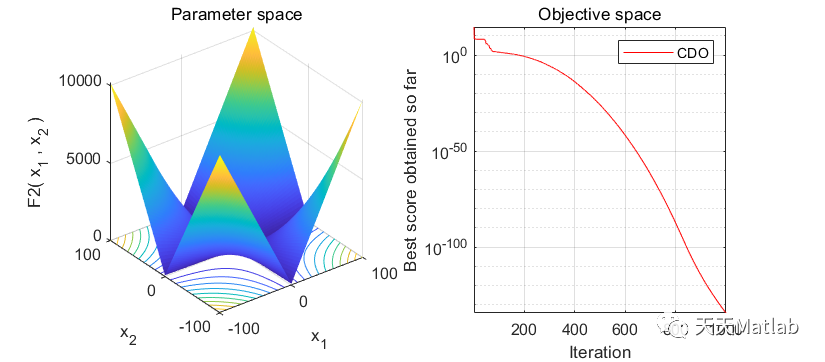
⛳️ 运行结果

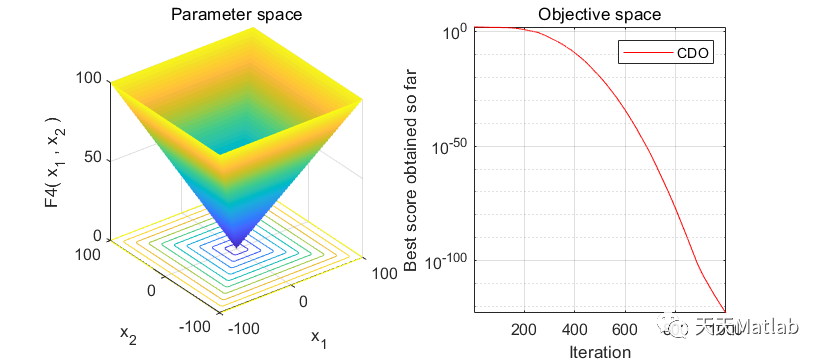
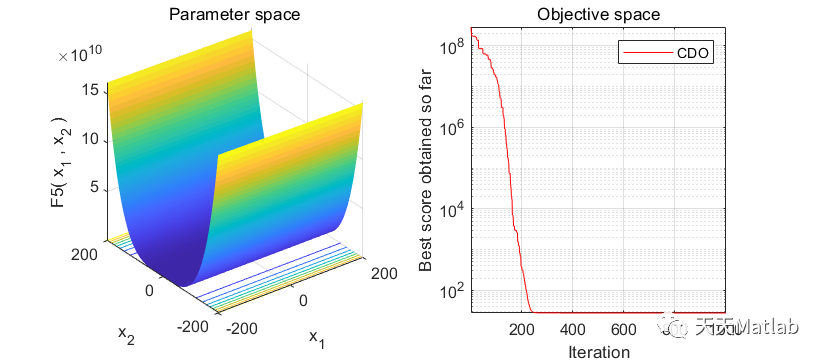
🔗 参考文献

本程序参考以下中文EI期刊，程序注释清晰，干货满满。

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合