【粒子群算法】基于双适应度粒子群算法求解单目标优化问题附matlab代码

1 简介

In any meta-heuristic algorithm, each search agent must move to the high-fitness areas in the search space while preserving its diversity. At first glance, there is no relationship between fitness and diversity, as two key factors to be considered in selecting a guide for the solutions. In other words, each of these factors must be evaluated in its specific and independent way. Since the independent ways to evaluate the fitness and diversity usually make any meta-heuristic consider these factors disproportionately to choose the guides, the solutions’ movements may be unbalanced. In this project, a novel version of the Particle Swarm Optimization (PSO) algorithm, named Dual Fitness PSO (DFPSO) is proposed. In this algorithm, not only fitness and diversity of the particles are properly evaluated, but also the abilities to evaluate these features are integrated to avoid the abovementioned problem in determining the global guide particles. ​

2 部分代码

%___________________________________________________________________%% Dual Fitness Particle Swarm Optimization (DFPSO) Algorithm        %%                                                                   %% Developed in MATLAB R2018b                                        %%                                                                   %% Inventor and programmer: Farshad Rezaei, PhD                      %%                                                                   %% e-Mail: farshad.rezaei@gmail.com                                  %%         f.rezaei@alumni.iut.ac.ir                                 %%                                                                   %% Homepage: https://www.linkedin.com/in/farshad-rezaei-5a92559a/    %%                                                                   %% Main paper: Rezaei, F., Safavi, H.R. Sustainable Conjunctive      %% Water Use Modeling Using Dual Fitness Particle Swarm Optimization %% Algorithm. Water Resour Manage 36, 989?006 (2022).               %% https://doi.org/10.1007/s11269-022-03064-w                        %%___________________________________________________________________%​% The initial parameters that you need are:%__________________________________________% fobj = @YourCostFunction% nx = number of your variables% lb= the lower bound of variables which can generally be a fixed number or a vector% ub= the upper bound of variables which can generally be a fixed number or a vector% notice: if the lower and upper bounds are not fixed for all variables, % they appear in the forms of the vectors "varmin" and "varmax", as illustrated in following​% To run DFPSO: [z_iter,z_final,pos_final]=DFPSO(np,nx,maxit,varmax,varmin,velmax,velmin,epsilon,k_max,k_min,fobj);%__________________________________________% Set the required parameters to run the DFPSO algorithm​% This code is for solving the minimization problems. To maximize a desired % cost function,please implement this code upon inverting the cost function​clcclearclose allticrun=1; % Maximum number of the algorithm runnings conductednp=50; % Number of search agentsmaxit=1000; % Maximum number of iterationsFunction_name='F1'; % Name of the test function that can be from F1 to F23epsilon=eps; % This parameter must be either set to eps (typically for the uni-modal functions) or zero (typically for the multi-modal or complex functions)k_max=0.9; % Upper bound of the inertia weightk_min=0.4; % Lower bound of the inertia weight[lb,ub,nx,fobj]=Objective_Function(Function_name); % Load details of the selected benchmark functionvarmax=ub*ones(1,nx); % Upper bound defined for the positions which can generally be a desired vectorvarmin=lb*ones(1,nx); % Lower bound defined for the positions which can generally be a desired vectorlimvel=0.1; % A ratio of the maximum distance in the search space to form the maximum velocity velmax=limvel*(varmax(1,1:nx)-varmin(1,1:nx)); % Upper bound defined for the velocitiesvelmin=-velmax; % Lower bound defined for the velocitiesz_iter_main=zeros(run,maxit);z_final_main=zeros(run);pos_final_main=zeros(run,nx);x1=zeros(maxit);y1=zeros(maxit);​% Run the DFPSO algorithm for "run" times for nrun=1:run    [z_iter,z_final,pos_final]=DFPSO(np,nx,maxit,varmax,varmin,velmax,velmin,epsilon,k_max,k_min,fobj);     z_iter_main(nrun,1:maxit)=z_iter(1:maxit);     z_final_main(nrun)=z_final;     pos_final_main(nrun,1:nx)=pos_final(1:nx);%      disp(['The best objective function value obtained by DFPSO = ',num2str(z_final_main(nrun))]);%      disp(['The best solution obtained by DFPSO = ','[',num2str(pos_final_main(nrun,1:nx)),']']);end​% Display the comprehensive resultsdisp(['The final statistical results calculated when implementing the DFPSO algorithm for ',num2str(run),' times are as follows:']);disp(['The average of the final objective function values calculated over ',num2str(run),' times = ',num2str(mean(z_final_main(1:run)))]);disp(['The median of the final objective function values calculated over ',num2str(run),' times = ',num2str(median(z_final_main(1:run)))]);disp(['The best of the final objective function values calculated over ',num2str(run),' times = ',num2str(min(z_final_main(1:run)))]);disp(['The standard deviation of the final objective function values calculated over ',num2str(run),' times = ',num2str(std(z_final_main(1:run)))]);​% Plot the chart of the objective function values obtained by DFPSO over the course of iterationsfor i=1:maxit    x1(i)=i;sum1=0;    for j=1:run        sum1=sum1+z_iter_main(j,i);    end    y1(i)=sum1/run;endsemilogy(x1,y1,'-r')xlabel('Iteration');ylabel('Average best-so-far');legend('DFPSO');hold ontime_dfpso = toc;disp(['Elapsed time of running the DFPSO for ',num2str(run),' times = ',num2str(time_dfpso),' seconds']);

3 仿真结果

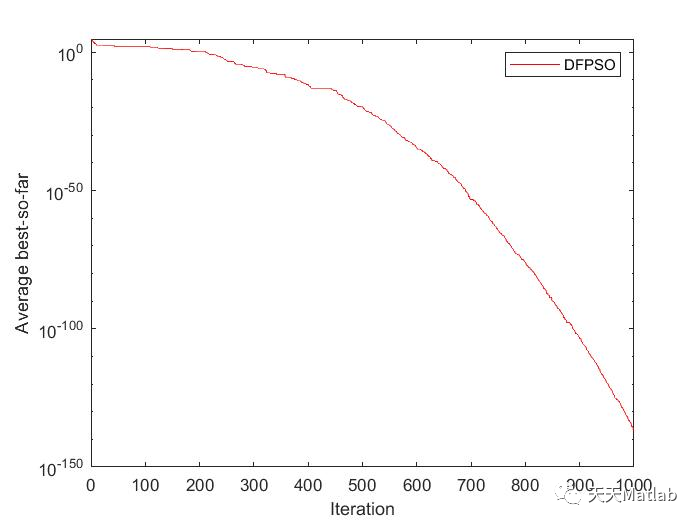
4 参考文献

Rezaei, F., Safavi, H.R. Sustainable Conjunctive Water Use Modeling Using Dual Fitness Particle Swarm Optimization Algorithm. Water Resour Manage 36, 989–1006 (2022)

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。