【通信】基于量子密钥分发密钥率仿真含Matlab源码

1 简介

基于量子密钥分发密钥率仿真​

2 完整代码

% the calculations from NEW%asymmetric case with immLac=0:0.0001:100; %distance between Alice and Bobfor G=[0.001,0.002,0.005]VM=6;VA=VM+1;VB=VM+1;V=VA;a=0.2;%the loss of fiber is 0.2dB/kmvel=0;eta=1;Lbc=0;yitaA=power(10,-a.*Lac/10); %channel losses in channel ACyitaB=power(10,-a.*Lbc/10); %channel losses in channel BCg=sqrt(2*(VB-1)./(yitaB.*eta.*(VB+1)));T=yitaA./2.*g.*g;eA=0.002;eB=0.002; %the excess noise of channel AC and BCeAIM=G*VM;eBIM=G*VM;XA=(1-yitaA)./yitaA+eA;XB=(1-yitaB)./yitaB+eB;Xhom=(vel+1-eta)/eta;%the noise introduced by Charlie's homdyne detectionseIM=eAIM+(1./yitaA).*(yitaB.*(eBIM-2)+2);etot=eA+(1./yitaA).*(yitaB.*(eB-2)+2+2*Xhom)+eIM; %the equivalent total excess noiseXline=1./T-1+etot;Xtot=Xline;beta=0.96; %reverse reconciliationa=V;b=T.*(V+Xtot);c=sqrt(T.*(V^2-1));IAB=log2((a+1)./(a+1-power(c,2)./(b+1)));% IAB=log2((T.*(V+Xtot)+1)./(T.*(1+Xtot)+1));IABfinal=beta*IAB;A=power(a,2)+power(b,2)-2*power(c,2);B=a.*b-power(c,2);lamd1=sqrt(0.5)*sqrt(A+sqrt(A.*A-4*power(B,2)));lamd2=sqrt(0.5)*sqrt(A-sqrt(A.*A-4*power(B,2)));%lamd3=sqrt(a-power(c,2)./(b+1));lamd3=a-power(c,2)./(b+1);XBE=((lamd1)/2+0.5).*log2((lamd1)/2+0.5)-((lamd1)/2-0.5).*log2((lamd1)/2-0.5)+((lamd2)/2+0.5).*log2((lamd2)/2+0.5)-((lamd2)/2-0.5).*log2((lamd2)/2-0.5)-(((lamd3)/2+0.5).*log2((lamd3)/2+0.5)-((lamd3)/2-0.5).*log2((lamd3)/2-0.5));K=IABfinal-XBE;semilogy(Lac,K);axis([0 50 10^(-6) 10^2])hold on;end%%%perfect asymmetric caseVM=6;VA=VM+1;VB=VM+1;V=VB;a=0.2;%the loss of fiber is 0.2dB/kmvel=0;eta=1;Lac=0:0.0001:100; %distance between Alice and BobLbc=0;yitaA=power(10,-a.*Lac/10); %channel losses in channel ACyitaB=power(10,-a.*Lbc/10); %channel losses in channel BCg=sqrt(2*(VB-1)./(yitaB.*eta.*(VB+1)));T=yitaA./2.*g.*g;eA=0.002;eB=0.002; %the excess noise of channel AC and BCXA=(1-yitaA)./yitaA+eA;XB=(1-yitaB)./yitaB+eB;Xhom=(vel+1-eta)/eta;%the noise introduced by Charlie's homdyne detectionsetot=eA+(1./yitaA).*(yitaB.*(eB-2)+2+2*Xhom); %the equivalent total excess noiseXline=1./T-1+etot;Xtot=Xline;beta=0.96; %reverse reconciliationa=V;b=T.*(V+Xtot);c=sqrt(T.*(V^2-1));IAB=log2((a+1)./(a+1-power(c,2)./(b+1)));% IAB=log2((T.*(V+Xtot)+1)./(T.*(1+Xtot)+1));IABfinal=beta*IAB;A=power(a,2)+power(b,2)-2*power(c,2);B=a.*b-power(c,2);lamd1=sqrt(0.5)*sqrt(A+sqrt(A.*A-4*power(B,2)));lamd2=sqrt(0.5)*sqrt(A-sqrt(A.*A-4*power(B,2)));%lamd3=sqrt(a-power(c,2)./(b+1));lamd3=a-power(c,2)./(b+1);XBE=((lamd1)/2+0.5).*log2((lamd1)/2+0.5)-((lamd1)/2-0.5).*log2((lamd1)/2-0.5)+((lamd2)/2+0.5).*log2((lamd2)/2+0.5)-((lamd2)/2-0.5).*log2((lamd2)/2-0.5)-(((lamd3)/2+0.5).*log2((lamd3)/2+0.5)-((lamd3)/2-0.5).*log2((lamd3)/2-0.5));K=IABfinal-XBE;semilogy(Lac,K,'r');axis([0 80 10^(-6) 10^2])hold on;​t=0:0.00001:1;L=50*(-log10(t));k=-log2(1-t);semilogy(L,k);xlabel('Transmission Distance [km]');ylabel('Secret Key Rate [bit/pulse]');legend('G_{IM}=0.001','G_{IM}=0.002','G_{IM}=0.005','ideal','PLOB bound')​

clc;    %%clear commandclear;  %%clear variablesclose all;  %%close files​%%%%%%%%%%%%%GMCS%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%alpha=0.2;        %db/kmVA=4;             %modulation varianceV=VA+1;beta=0.95;        %reconciliation efficiencyeta=0.6;          %quantum efficiencyvel=0.1;          %electronic noise epsilon=0.0001;   %excess noise​L=0:1:500;KeyRate_hom = zeros(length(L), 1);%Holevo bound using homodyneKeyRate_het = zeros(length(L), 1);%Holevo bound using heterdyne​% epsilon=[0.01,0.03,0.05,0.07];​% for i = 1: length(epsilon)% figure(2);   % [KeyRate_hom,KeyRate_het] = GMCScvqkd(L, alpha, VA, V, eta, vel, epsilon(i), beta);% semilogy(L, KeyRate_hom, '-b');% hold on;% % semilogy(L, KeyRate_het, '-b');% % hold on;% end​[KeyRate_hom,KeyRate_het] = GMCScvqkd(L, alpha, VA, V, eta, vel, epsilon, beta);​​figure(2);semilogy(L, KeyRate_hom, '-b');grid on;box on;hold on;​figure(2);semilogy(L, KeyRate_het, '-r');hold on;​xlabel('Distance[km]');ylabel('Security Key Rate [bits/pulse]');title('Comparison of protocols');​%%%%%%%%%%%%%%%%%%DMCS%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%​alpha=0.2;         %db/kmVA=0.3;              %modulation varianceV=VA+1;beta=0.95;      %reconciliation efficiencyeta=0.6;          %quantum efficiencyvel=0.1;        %electronic noise epsilon=0.00001;        %excess noise​L=0:1:500;KeyRate_hom_dct = zeros(length(L), 1);%Holevo bound using homodyneKeyRate_het_dct = zeros(length(L), 1);%Holevo bound using heterdyne​[KeyRate_hom_dct,KeyRate_het_dct] = DMCScvqkd(L, alpha, VA, V, eta, vel, epsilon, beta);​figure(2);semilogy(L, KeyRate_hom_dct, ':b');hold on;​figure(2);semilogy(L, KeyRate_het_dct, ':r');hold on;​%%%%%%%%%%%%%%%%%%decoy%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%L = 0:1:500;mu = 0.1;nu = 0.05;etab = 0.4;etad = 0.15;pd = 2*10^(-12);edet = 0.01;fEmu = 1;​% edet = 0.01;% edet = [0.01,0.03,0.05,0.07];% K = decoydvqkd(L0, 0.1, 0.05, 0.4, 0.15, 2*10^(-6), edet, 1);​K = decoydvqkd(L, mu, nu, etab, etad, pd, edet, fEmu);figure(2); semilogy(L, K,'--r');hold on;​​% for i = 1: length(edet) % K = decoydvqkd(L, mu, nu, etab, etad, pd, edet(i), fEmu);% figure(2); % semilogy(L, K,'--r');% hold on;% end​% for i = 1: length(edet)%    K = decoydvqkd(L0, 0.1, 0.05, 0.4, 0.17, 2*10^(-6), edet(i), 1);%    figure(2); %    h_dvt = semilogy(L0, K);%    hold on;% end​%%%%%%%%%%%%%%%%%%MDICVQKD%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%alpha=0.2;         %db/kmVM=80;VA=VM+1;VB=VM+1;V=VB;beta=1;        %reconciliation efficiencyeta=1;         %quantum efficiencyvel=0;         %electronic noise eA=0.0001;     %excess noiseeB=0.0001;Lac=0:1:500; %distance between Alice and BobLbc=0;​K=MDIcvqkd(Lac, Lbc, alpha, VA, VB, V, eta, vel, eA, eB, beta);​semilogy(Lac,K,'--r');hold on;​Lac=0:1:100; %distance between Alice and BobLbc=0:1:100;​K2=MDIcvqkd(Lac, Lbc, alpha, VA, VB, V, eta, vel, eA, eB, beta);​semilogy(Lac+Lbc,K2,'--b');hold on;​​​​%%%%%%%%%%%%%%%%%%PLOB%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%L=0:1:500;t=power(10,-alpha.*L/10); %channel losses in channel AC% t=0:0.0000001:1;L=50*(-log10(t));k=-log2(1-t);semilogy(L,k);kZero = 1*1e-15*ones(1,length(L));%Holevo bound using homodyne​legend('GMCS Homodyne','GMCS Heterdyne','DMCS Homedyne','DMCS Heterdyne','DecoyDVQKD','MDI-QKD asymmetric','MDI-QKD symmetric','PLOB');​​y1_y2=[KeyRate_hom';kZero];  % 是一个2×ls的矩阵，第一行为y1，第二行为y2maxY1vsY2=max(y1_y2); % 1×ls的是一个行向量，表示y1_y2每一列的最大值，即x相同时、y1与y2的的最大值minY1vsY2=min(y1_y2); % 1×ls的是一个行向量，表示y1_y2每一列的最小值，即x相同时、y1与y2的的最小值yForFill=[maxY1vsY2,fliplr(minY1vsY2)];xForFill=[L,fliplr(L)];% fill(xForFill,yForFill,'r','FaceColor','r','FaceAlpha',0.5,'EdgeAlpha',1,'EdgeColor','r'); % 填充并设置图形格式% fill(xForFill,yForFill,'r'); % 填充并设置图形格式​

function K = decoydvqkd(L, mu, nu, etab, etad, pd, edet, fEmu)​% L = 0:0.01:170;% mu = 0.1;% nu = 0.05;% etab = 0.4;% etad = 0.15;% pd = 2*10^(-6);% edet = 0.01;% fEmu = 1;​q0 = 0.5;eta = etab*etad*10.^(-0.02*L);e = 0.5;Y0 = 2*pd;Qmu = Y0 + 1 - exp(-eta .*mu);Qnu = Y0 + 1 - exp(-eta.*nu);Emu  = (e*Y0 + edet*(1 - exp(-eta*mu)))./Qmu;Enu  = (e*Y0 + edet*(1 - exp(-eta*nu)))./Qnu;Y1 = (mu/(mu*nu - nu^2))*(Qnu*exp(nu) - Qmu*(nu^2)*exp(mu)/(mu^2) - (mu^2 - nu^2)*Y0/(mu^2));Q1min = (((mu^2)*exp(-mu)/(mu*nu-nu^2)))*(Qnu.*exp(nu) - Qmu*(nu^2)*exp(mu)/(mu^2) - (mu^2 - nu^2)*Y0/(mu^2));e1max = (Enu.*Qnu*exp(nu) - e*Y0)./(Y1*nu);H2E = -Emu.*log2(Emu) - (1-Emu).*log2(1-Emu);H2e = -e1max.*log2(e1max) - (1-e1max).*log2(1-e1max);K = q0*(-Qmu.*H2E.*fEmu + Q1min.*(1 - H2e));end​​

function [KeyRate_hom_dct,KeyRate_het_dct] = DMCScvqkd(L, alpha, VA, V, eta, vel, epsilon, beta)​I_AB_hom_dct = zeros(length(L), 1);%shannon entropy using homodyneI_AB_het_dct = zeros(length(L), 1);%shannon entropy using heterdynekappa_BE_hom_dct = zeros(length(L), 1);%Holevo bound using homodynekappa_BE_het_dct = zeros(length(L), 1);%Holevo bound using heterdyneKeyRate_hom_dct= zeros(length(L), 1);KeyRate_het_dct= zeros(length(L), 1);​for i=1:length(L)   %%ORIGIN        T=10^(-alpha/10*L(i));     %T        kappa_line=epsilon-1+1/T;  %    kappa_hom = (1-eta+vel) / eta; %    kappa_het = (2-eta+2*vel) / eta; %    kappa_tot_hom = kappa_line + kappa_hom/T;  %    kappa_tot_het = kappa_line + kappa_het/T; %​​    I_AB_hom_dct(i) = 0.5 * log2( (V+kappa_tot_hom) / (1+kappa_tot_hom) ); %    I_AB_het_dct(i) = log2( (V+kappa_tot_het) / (1+kappa_tot_het) );%​      %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%      eps_0=1/2 * exp(-VA/2) * (  cosh( VA/2) + cos(VA/2)    );      eps_2=1/2 * exp(-VA/2) * (  cosh( VA/2) - cos(VA/2)    );​      eps_1=1/2 * exp(-VA/2) * (  sinh( VA/2) + sin(VA/2)    );      eps_3=1/2 * exp(-VA/2) * (  sinh( VA/2) - sin(VA/2)    );​      Z_4 = VA *( eps_0^(3/2) * eps_1^(-1/2) + eps_1^(3/2) * eps_2^(-1/2) + eps_2^(3/2) * eps_3^(-1/2) + eps_3^(3/2) * eps_0^(-1/2) );      %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%            A_dct = V^2 + T^2*(V+kappa_line)^2-2*T*Z_4^2;    B_dct = (T*V^2 + T* V* kappa_line - T*Z_4^2)^2;    lamda_1_dct = sqrt( 0.5 * (A_dct + sqrt(A_dct^2 - 4*B_dct)) );   %symplectic eigenvalues    lamda_2_dct = sqrt( 0.5 * (A_dct - sqrt(A_dct^2 - 4*B_dct)) );        C_hom_dct = ( A_dct*kappa_hom + V*sqrt(B_dct) + T*(V+kappa_line) )/ (T*(V+kappa_tot_hom));    D_hom_dct = sqrt(B_dct) * (V+sqrt(B_dct)*kappa_hom) / (T*(V+kappa_tot_hom)) ;    lamda3_hom_dct = sqrt( 0.5 * (C_hom_dct + sqrt(C_hom_dct^2 - 4*D_hom_dct)) );    lamda4_hom_dct = sqrt( 0.5 * (C_hom_dct - sqrt(C_hom_dct^2 - 4*D_hom_dct)) );​    C_het_dct = ( A_dct*kappa_het^2 + B_dct + 1 + 2*kappa_het*(V*sqrt(B_dct)+T*(V+kappa_line) ) + 2*T*Z_4^2 )/ (T*(V+kappa_tot_het))^2;    D_het_dct = ( (V+sqrt(B_dct)*kappa_het) / (T*(V+kappa_tot_het)) )^2;    lamda3_het_dct = sqrt( 0.5 * (C_het_dct + sqrt(C_het_dct^2 - 4*D_het_dct)) );    lamda4_het_dct = sqrt( 0.5 * (C_het_dct - sqrt(C_het_dct^2 - 4*D_het_dct)) );​ kappa_BE_hom_dct(i) = G1( lamda_1_dct)+G1(lamda_2_dct)-G1( lamda3_hom_dct)-G1(lamda4_hom_dct); kappa_BE_het_dct(i) = G1(lamda_1_dct)+G1(lamda_2_dct)-G1(lamda3_het_dct)-G1(lamda4_het_dct);  KeyRate_hom_dct(i)=beta*I_AB_hom_dct(i) - kappa_BE_hom_dct(i); KeyRate_het_dct(i)=beta*I_AB_het_dct(i) - kappa_BE_het_dct(i);  if(KeyRate_hom_dct(i)<0)     KeyRate_hom_dct(i)=1e-10; end if(KeyRate_het_dct(i)<0)     KeyRate_het_dct(i)=1e-10; end​end ​KeyRate_hom_dct = KeyRate_hom_dct;KeyRate_het_dct = KeyRate_het_dct;end​​

function y = G1(x)%UNTITLED3 Summary of this function goes here%   Detailed explanation goes hereif((x<0) || (x==0))     y=0;    else       y=((x+1)/2)*log2((x+1)/2)-((x-1)/2)*log2((x-1)/2);end​end​​

function [KeyRate_hom,KeyRate_het] = GMCScvqkd(L, alpha, VA, V, eta, vel, epsilon, beta)​I_AB_hom = zeros(length(L), 1);%shannon entropy using homodyneI_AB_het = zeros(length(L), 1);%shannon entropy using heterdynekappa_BE_hom = zeros(length(L), 1);%Holevo bound using homodynekappa_BE_het = zeros(length(L), 1);%Holevo bound using heterdyne​for i=1:length(L)   %%ORIGIN        T=10^(-alpha/10*L(i));     %T        kappa_line=epsilon-1+1/T;  %    kappa_hom = (1-eta+vel) / eta; %    kappa_het = (2-eta+2*vel) / eta; %    kappa_tot_hom = kappa_line + kappa_hom/T;  %    kappa_tot_het = kappa_line + kappa_het/T; %​    I_AB_hom(i) = 0.5 * log2( (V+kappa_tot_hom) / (1+kappa_tot_hom) ); %    I_AB_het(i) = log2( (V+kappa_tot_het) / (1+kappa_tot_het) );%​    A = V^2*(1-2*T) + 2*T + (T*(V+kappa_line))^2;%    B = (T * (1+V*kappa_line))^2;%    lamda_1 = sqrt( 0.5 * (A + sqrt(A^2 - 4*B)) );%symplectic eigenvalues %    lamda_2 = sqrt( 0.5 * (A - sqrt(A^2 - 4*B)) );%​    C_hom = ( A*kappa_hom + V*sqrt(B) + T*(V+kappa_line) ) / (T*(V+kappa_tot_hom)); %    D_hom = sqrt(B) * (V+sqrt(B)*kappa_hom) / (T*(V+kappa_tot_hom)); %    C_het = ( A*kappa_het^2 + B + 1 + 2*kappa_het*(V*sqrt(B)+T*(V+kappa_line)) + 2*T*(V^2-1)) / (T*(V+kappa_tot_het))^2;%    D_het = ( (V+sqrt(B)*kappa_het) / (T*(V+kappa_tot_het)) )^2;%    lamda3_hom = sqrt( 0.5 * (C_hom + sqrt(C_hom^2 - 4*D_hom)) ); %    lamda4_hom = sqrt( 0.5 * (C_hom - sqrt(C_hom^2 - 4*D_hom)) ); %    lamda3_het = sqrt( 0.5 * (C_het + sqrt(C_het^2 - 4*D_het)) ); %    lamda4_het = sqrt( 0.5 * (C_het - sqrt(C_het^2 - 4*D_het)) ); %​ kappa_BE_hom(i) = G1(lamda_1)+G1(lamda_2)-G1( lamda3_hom)-G1( lamda4_hom); kappa_BE_het(i) = G1(lamda_1)+G1(lamda_2)-G1( lamda3_het)-G1( lamda4_het);​end​KeyRate_hom = beta*I_AB_hom - kappa_BE_hom;KeyRate_het = beta*I_AB_het - kappa_BE_het;end​​

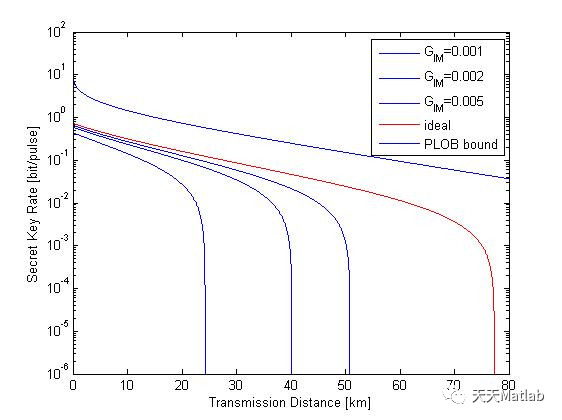
3 仿真结果

4 参考文献

[1]杨思源. 基于SC-LDPC码的连续变量量子密钥分发研究[D]. 东华大学.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。