一个计算同调群的例子

原创已于 2024-02-13 16:07:29 修改 · 1.8k 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#拓扑学

于 2024-02-06 21:20:16 首次发布

持续同调文章阅读专栏收录该内容

6 篇文章

订阅专栏

本文通过一个具体的例子介绍了如何计算环面的同调群，涉及链群、边界映射和复形的结构，展示了0维、1维和2维复形的同调特征.

一个计算同调群的例子

今天在B站看到一个计算同调群的视频，记录一下。

视频网址：https://www.bilibili.com/video/BV1Nv42117mn/?spm_id_from=333.337.search-card.all.click&vd_source=84d747ae63525b79ef57f7be80b7c9f9

环面可由四边形黏合而成，对其做三角剖分，并给定点、边、面，其中对应边必须与对应箭头粘合，给面定向且要求在边 $c$ 引导的方向相反。考虑下图：
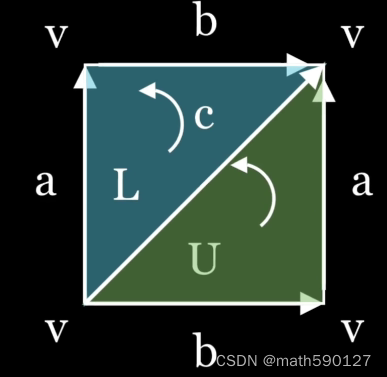
在这里插入图片描述
有链群（chain group） $0→C2→C1→C0→00\rightarrow C_2\rightarrow C_1 \rightarrow C_0 \rightarrow 0$ ，且从每个 $C_{i+1}$ 到 $C_i$ 的映射 $∂i\partial_i$ 被称为边缘映射（boundary map）； $C_n$ 代表维数为 $n$ 的复形，即 $C_2=\{U,L\},C_1=\{a,b,c\},C_0=\{v\}$ 。计算得：
$∂0(v)=0,Ker∂0=<v>,Im∂1=<0>∂1(a)=∂1(b)=∂1(c)=v−v=0,Ker∂1=<a,b,c>,Im∂2=<a+b−c>∂2(U)=a+b−c,∂2(L)=−a−b+c,Ker∂2=<U+L>,Im∂3=<0>\partial_0(v)=0,Ker\partial_0=<v>,Im\partial_1=<0>\\ \partial_1(a)=\partial_1(b)=\partial_1(c)=v-v=0,Ker\partial_1=<a,b,c>,Im\partial_2=<a+b-c>\\ \partial_2(U)=a+b-c,\partial_2(L)=-a-b+c,Ker\partial_2=<U+L>,Im\partial_3=<0>$
接着可以计算同调群（均在同构意义下）：
$H0=Ker∂0/Im∂1=Z/0=ZH1=Ker∂1/Im∂2=Z3/Z=Z2H2=Ker∂2/Im∂3=Z/0=ZH_0=Ker\partial_0/Im\partial_1=\mathbb{Z}/0=\mathbb{Z} \\ H_1=Ker\partial_1/Im\partial_2=\mathbb{Z}^3/\mathbb{Z}=\mathbb{Z}^2 \\ H_2=Ker\partial_2/Im\partial_3=\mathbb{Z}/0=\mathbb{Z}$
意义：0维复形结果为 $Z\mathbb{Z}$ ，即0维本质点只会有一个，即 $v$ ；1维复形结果为 $Z2\mathbb{Z}^2$ ，即1维本质边有两条，即 $a$ 和 $b$ （环面上看就是经线和纬线，其他线要么同伦于二者之一，要么可以缩成一点）；2维复形结果为 $Z\mathbb{Z}$ ，即2维本质面只会有一个（环面上看就是环面自身）。