全局B样条拟合

一、问题描述

  对于给定的一系列任意维数的数据点(维数大于1)，进行全局B样条拟合，使曲线满足一定连续性(C1、C2或更高阶连续)，同时支持多种拟合条件：
  (1)给定数据点与拟合误差；
  (2)给定数据点与控制点个数

二、多种拟合条件

(1)给定数据点与拟合误差

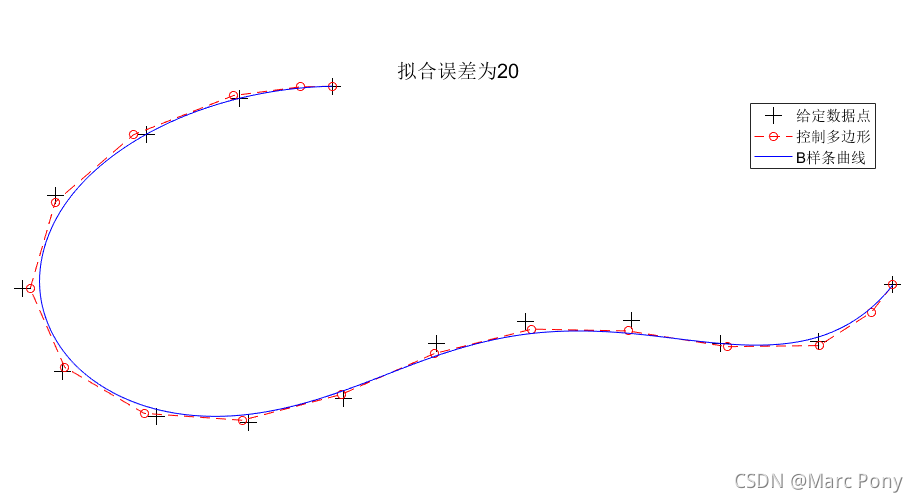
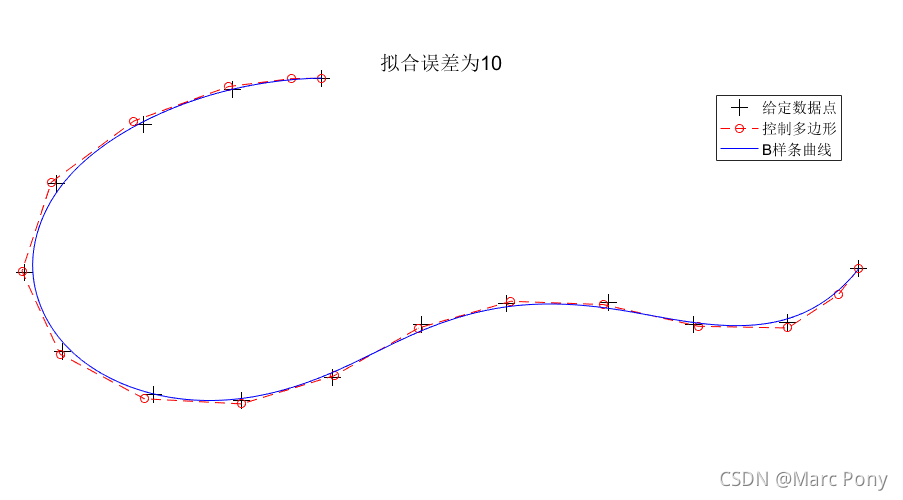
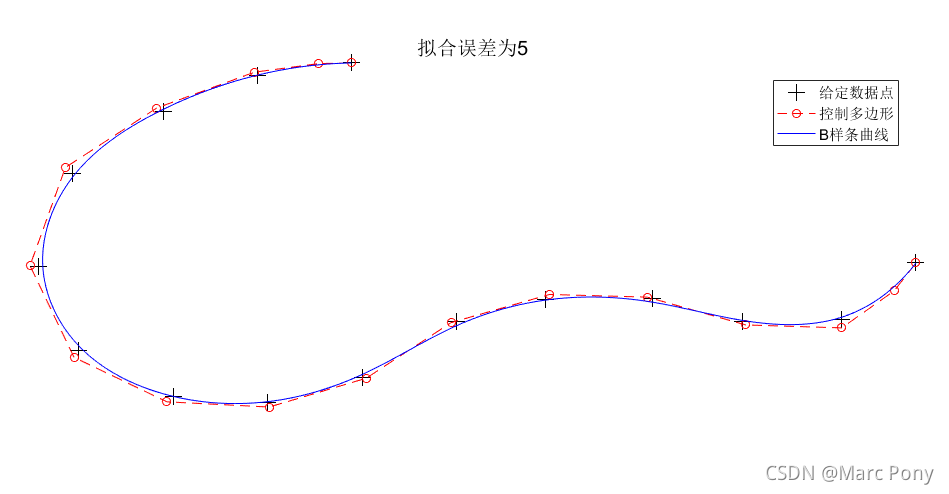
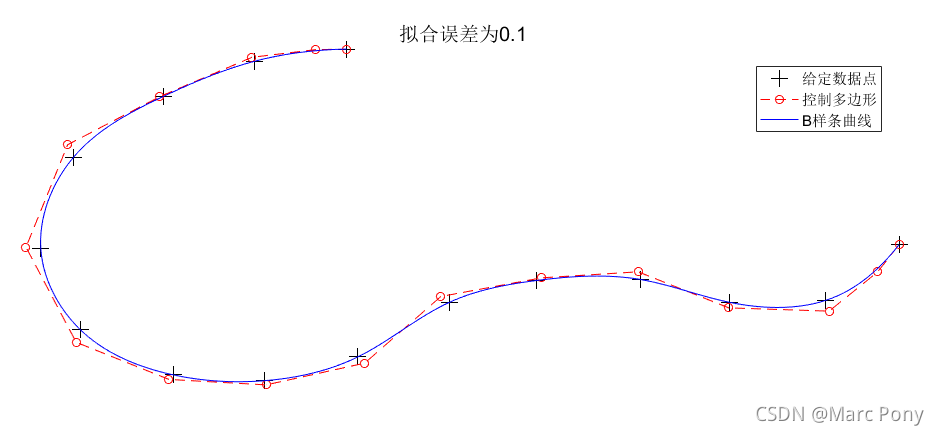
(2)给定数据点与控制点个数

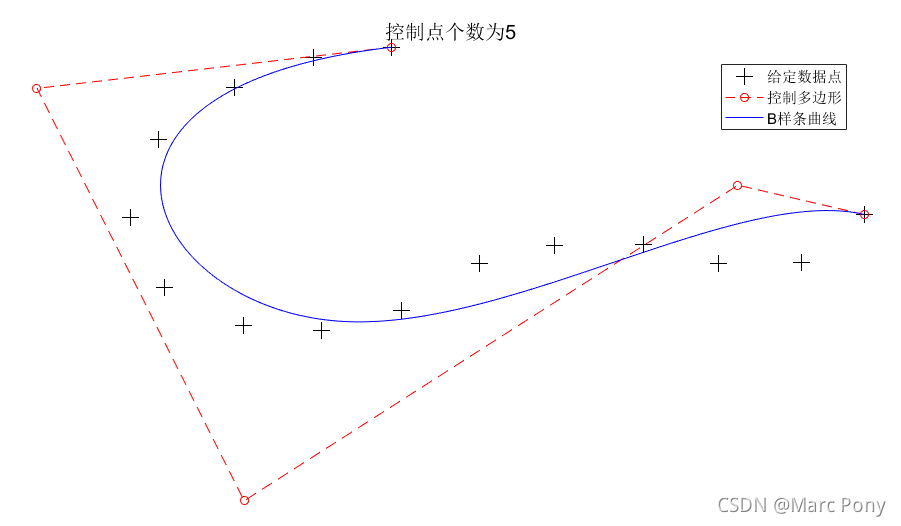
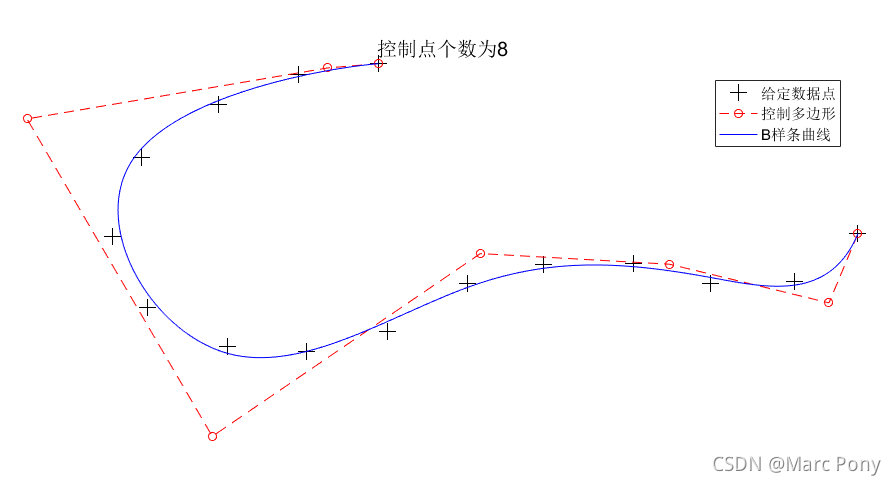
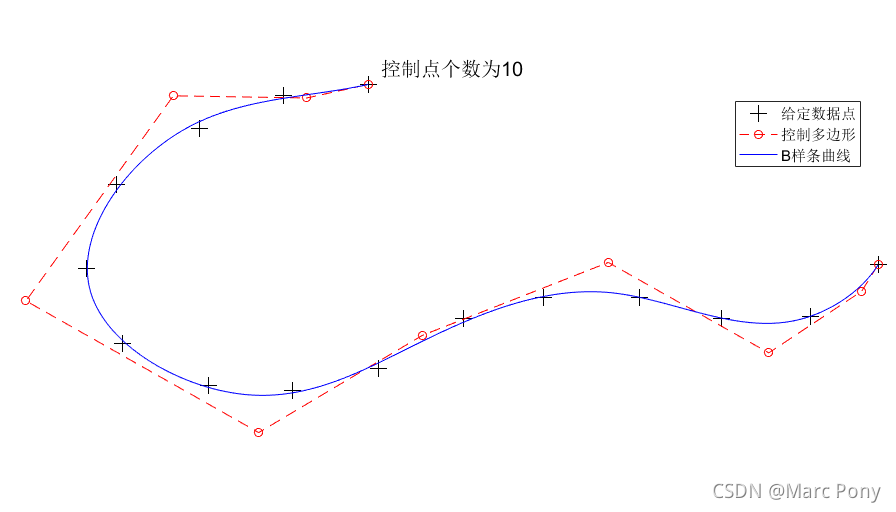
三、拟合对比插值的优缺点

(1)优点

  （1)拟合得到的曲线更加平滑(二阶导矢更小)，给定的拟合误差越大，拟合得到曲线的二阶导矢越小，曲线越平滑。如下图，有序数据点分别由半径为20，10，5的圆弧离散化而来，分别对数据点进行3次B样条插值与3次B样条拟合(拟合误差取0.2)。可以看到，3次B样条插值则精确经过每一个数据点，但在圆弧连接处，二阶导矢波动较大；3次B样条拟合则精确经过起点与终点，但不保证经过其他数据点(拟合误差在0.2以内)，在圆弧连接处，二阶导矢波动较小。


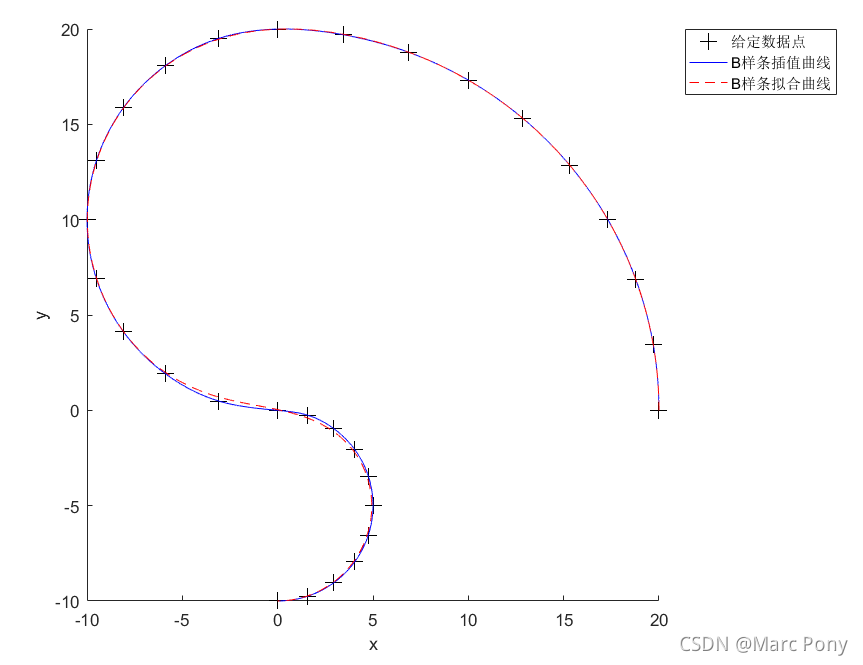
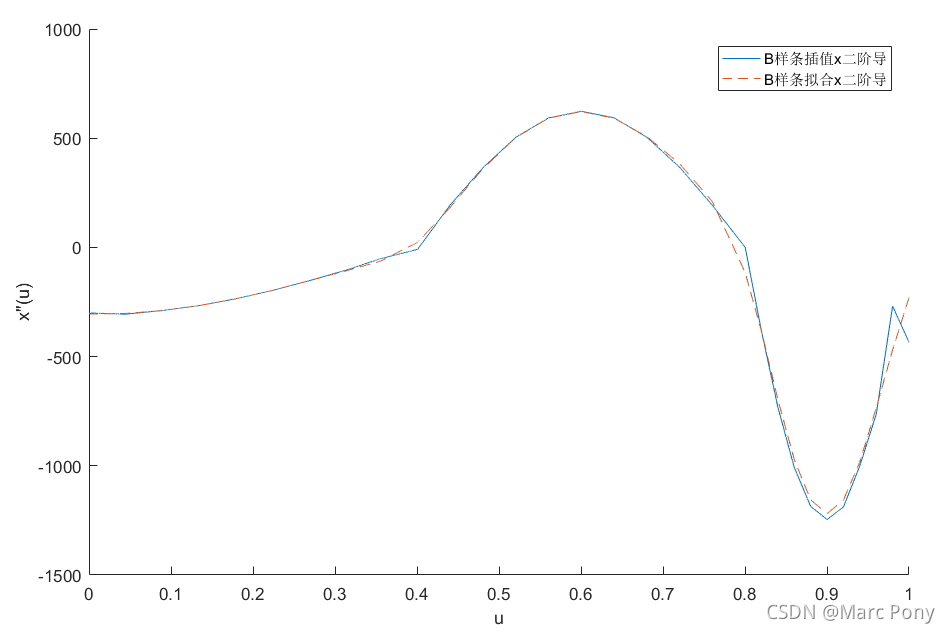
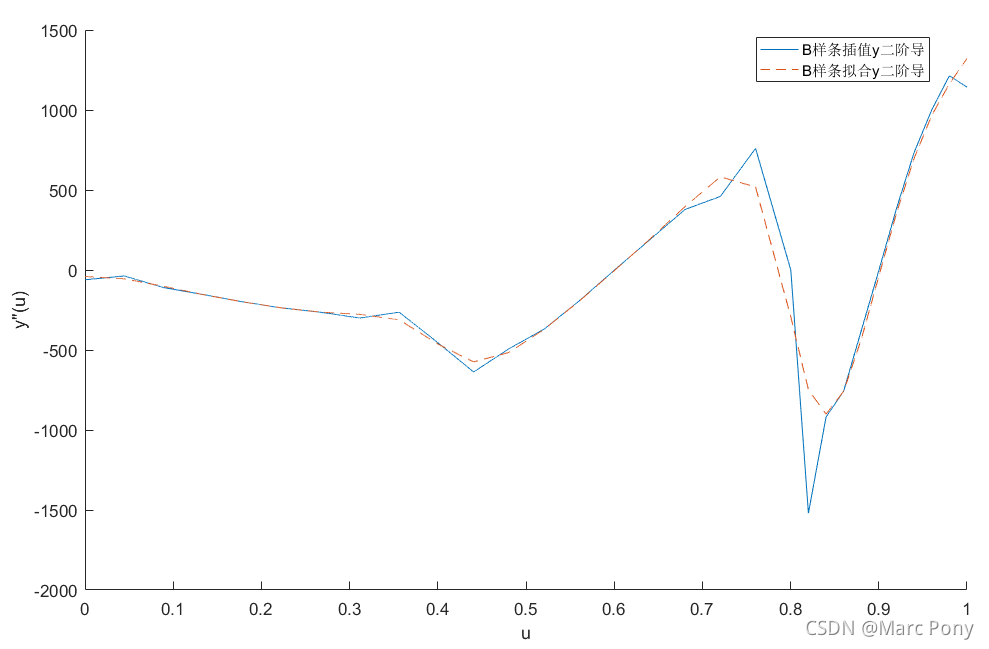
  （2)B样条拟合相对于B样条插值，可能只需要更少的控制点与节点个数便可以表达大量的有序数据点。

(2)缺点

  （1)B样条拟合计算量更大(主要是矩阵乘法，而矩阵乘法时间复杂度大)，且需要多次迭代计算。
  （2)B样条拟合不精确经过给定点(除了起点与终点)，影响路径精度。