最小包围球(附完整代码)

一、问题描述

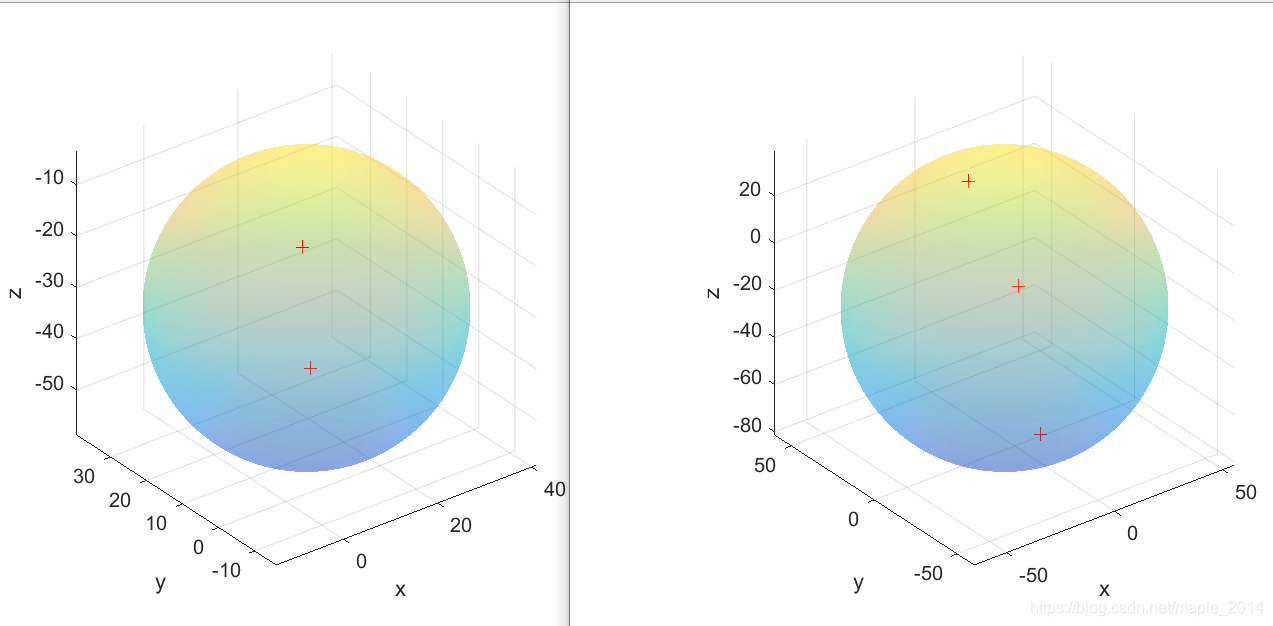
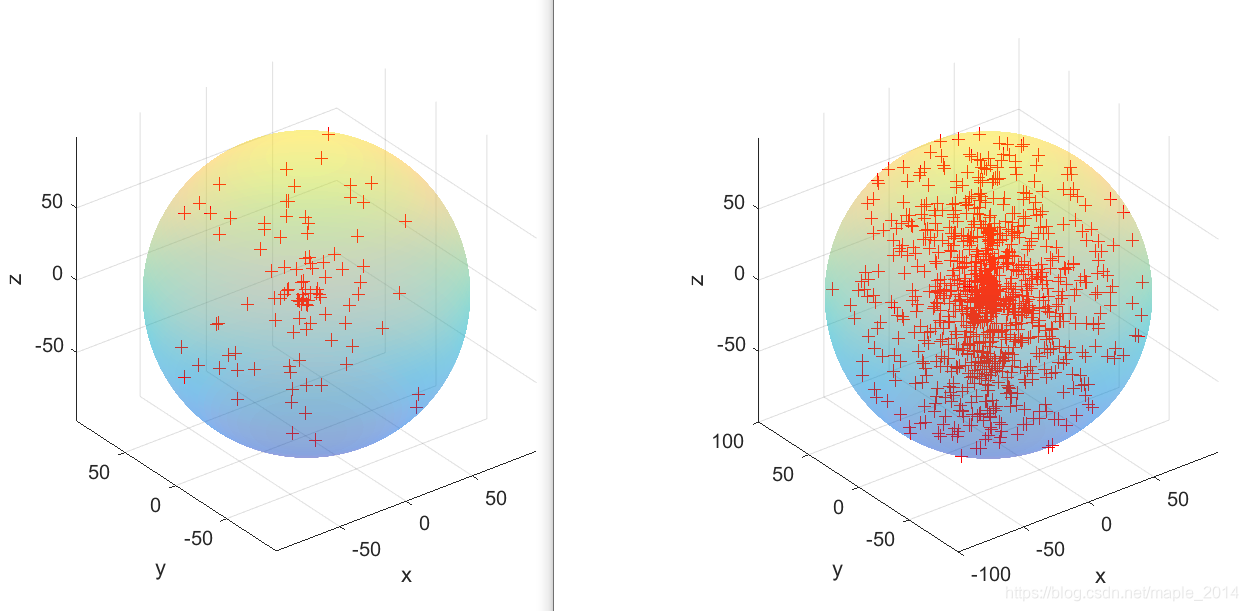
  给定空间$n$个点，计算最小包围球，使得所有给定点均在球面以内(包括在球面上)。

二、算法步骤

  最小包围球算法可以在最小覆盖圆算法的基础上修改得到：(1)将平面不共线三点确定一个圆的算法改成空间不共线三点确定一个圆的算法(详见博文:空间圆弧路径参数化)；（2）增加一个内循环，计算空间不共面四点确定一个球面的算法（详见博文：任意四面体的外接球/三维空间不共面四点确定唯一球面）。

三、MATLAB代码

%{
   
   
Function: draw_sphere
Description: 画球面
Input: 球心sphereCenter，球半径radius
Output: 无
Author: Marc Pony(marc_pony@163.com)
%}
function draw_sphere(sphereCenter, radius)
[x,y,z] = sphere(200);
x = x * radius + sphereCenter(1);
y = y * radius + sphereCenter(2);
z = z * radius + sphereCenter(3);
h = surf(x, y, z);
xlabel('x')
ylabel('y')
zlabel('z')
set(h, 'FaceAlpha', 0.3, 'MarkerEdgeColor', 'none')
shading interp
end

%{
   
   
Function: get_circle_center_3D
Description: 求空间三点确定的圆周的圆心
Input: 空间三个点a,b,c
Output: 空间圆周圆心center
Author: Marc Pony(marc_pony@163.com)
%}
function center = get_circle_center_3D(a, b, c)
x1 = a(1);
y1 = a(2);
z1 = a(3);
x2 = b(1);
y2 = b(2);
z2 = b(3);
x3 = c(1);
y3 = c(2);
z3 = c(3);
x4 = 0.5 * (x1 + x2);
y4 = 0.5 * (y1 + y2);
z4 = 0.5 * (z1 + z2);

x5 = 0.5 * (x2 + x3);
y5 = 0.5 * (y2 + y3);
z5 = 0.5 * (z2 + z3);

a11 = x2 - x1;
a12 = y2 - y1;
a13 = z2 - z1;
b1 = x4 * a11 + y4 * a12 + z4 * a13;

a21 = x3 - x2;
a22 = y3 - y2;
a23 = z3 - z2;
b2 = x5