采用梯形速度规划生成S形速度规划曲线(附代码)

一、问题描述

  梯形速度规划是最快也是最简单的速度规划方法。由于其速度连续但不平滑，加速度可控但会跳变，加加速度不可控，通常会引起受控对象震动，控制效果较差。S形速度规划由于其速度连续且平滑，加速度可控且连续，加加速度可控，控制效果好，广泛用于工业现场。但是，S形速度规划算法较复杂，在某些条件下，需要迭代计算进行规划，计算时间稍长。那么，有没有这样的方法：采用简单的梯形速度规划方法得到位置曲线，再通过一些方法，生成平滑的S形位置曲线？有的！本文提供了两种方法，效果如下：

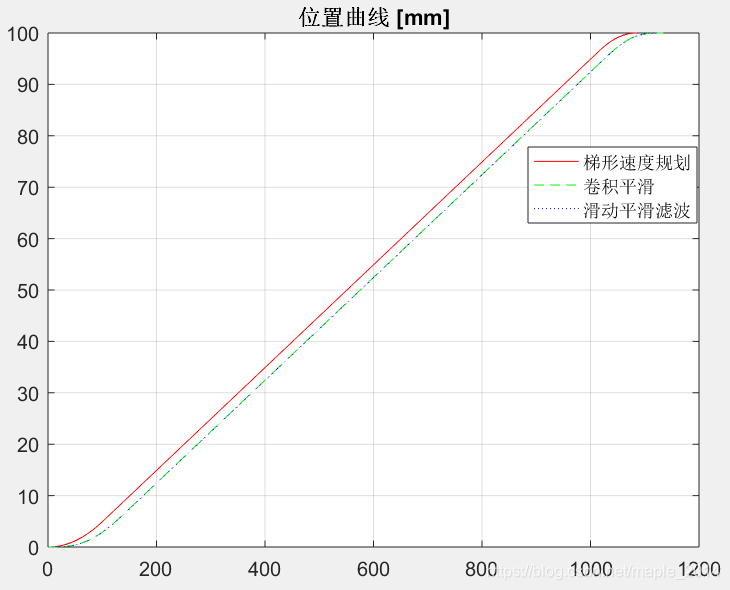
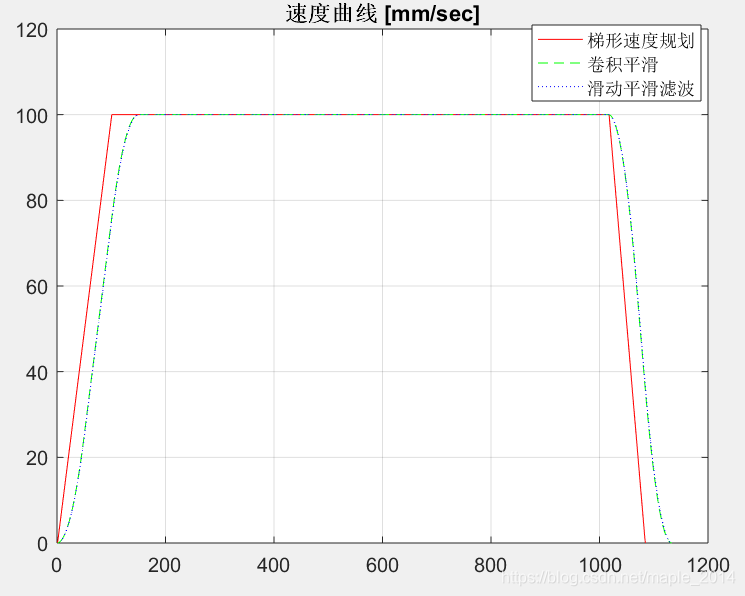
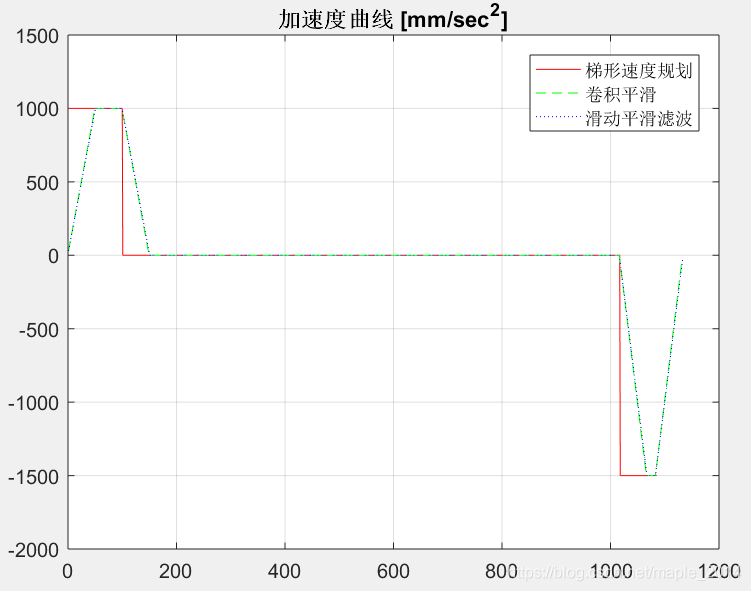
二、MATLAB代码

  计算两列数据的卷积：

%{
Function: my_conv
Description: 计算两列数据的卷积
Input: 数据列u，数据列v
Output: 数据列w
Author: Marc Pony(marc_pony@163.com)
Date: 2020.04.06
%}
function w = my_conv(u, v)
m = length(u);
n = length(v);
count = m + n - 1;
w = zeros(count, 1);
for k = 1 : count
    w(k) = 0.0;
    startIndex = max([1, k - n + 1]);
    endIndex = min([k, m]);
    for j = startIndex : endIndex
        w(k) = w(k) + u(j) * v(k - j + 1);
    end
end
end

  梯形速度规划：

%{
Function: trapezoidal_velocity_planning
Description: 梯形速度规划
Input: 运动参数motionParams
Output: 规划好了的运动参数motionParams，状态变量sta(1表示成功，0表示失败)
Author: Marc Pony(marc_pony@163.com)
Date: 2020.04.06
%}
function [motionParams, sta] = trapezoidal_velocity_planning(motionParams)
sta = 1;
if (motionParams.vs < motionParams.ve)
    if (motionParams.L + eps < (motionParams.ve * motionParams.ve - motionParams.vs * motionParams.vs) / (2.0 * motionParams.acc))
        sta = 0;
        return;
    end
elseif (motionParams.vs > motionParams.ve)
    if (motionParams.L + eps < (motionParams.vs * motionParams.vs - motionParams.ve * motionParams.ve) / (2.0 * motionParams.dec))
        sta = 0;
        return;
    end
else
    %to do nothing
end

motionParams.vm = sqrt((2.0 * motionParams.acc * motionParams.dec * motionParams.L + motionParams.dec * motionParams.vs * motionParams.vs + motionParams.acc * motionParams.ve * motionParams.ve) / (motionParams.acc + motionParams.dec));
if (motionParams.vm > motionParams.vc)
    motionParams.vm = motionParams.vc;
end

motionParams.T1 = (motionParams.vm - motionParams.vs) / motionParams.acc;
motionParams.T3 = (motionParams.vm - motionParams.ve) / motionParams.dec;

motionParams.L1 = 0.5 * (motionParams.vm + motionParams.vs) * motionParams.T1;
motionParams.L3 = 0.5 * (motionParams.vm + motionParams.ve) * motionParams.T3;
motionParams.L2 = motionParams.L - motionParams.L1 - motionParams.L3;
motionParams.T2 = motionParams.L2 / motionParams.vm;

motionParams.t1 = motionParams.T1;
motionParams.t2 = motionParams.t1 + motionParams.T2;
motionParams.t3 = motionParams.t2 + motionParams.T3;
motionParams.totalT = motionParams.t3;

motionParams.s1 = motionParams.L1;
motionParams.s2 = motionParams.s1 + motionParams.L2;
motionParams.s3 = motionParams.s2 + motionParams.L3;
end

  梯形速度规划的主轴插补：

%{
Function: main_axis_interpolation_for_trapezoidal_velocity
Description: 梯形速度规划的主轴插补
Input: 已经规划好了的运动参数motionParams
Output: 主轴位置pos(mm)、主轴速度vel(mm/s)、主轴加速度acc(mm/s^2)
Author: Marc Pony(marc_pony@163.com)
Date: 2020.04.06
%}
function [pos, vel, acc] = main_axis_interpolation_for_trapezoidal_velocity(motionParams)
if (motionParams.t < motionParams.t1)
    pos = motionParams.vs * motionParams.t + 0.5 * motionParams.acc * motionParams.t * motionParams.t;
    vel = motionParams.vs + motionParams.acc * motionParams.t;
    acc = motionParams.acc;
elseif (motionParams.t < motionParams.t2)
    pos = motionParams.L1 + (motionParams.t - motionParams.t1) * motionParams.vm;
    vel = motionParams.vm;
    acc = 0.0;
elseif (motionParams.t < motionParams.t3)
    pos = motionParams.L1 + motionParams.L2 + motionParams.vm * (motionParams.t - motionParams.t2) - 0.5 * motionParams.dec * (motionParams.t - motionParams.t2) * (motionParams.t - motionParams.t2);
    vel = motionParams.vm - motionParams.dec *(motionParams.t - motionParams.t2);
    acc = -motionParams.dec;
else
    motionParams.t = motionParams.totalT;
    pos = motionParams.L;
    vel = motionParams.ve;
    acc = -motionParams.dec;
end

end

  采用梯形速度规划生成S形速度曲线(卷积平滑方法和滑动平滑滤波方法)：

clc;
clear;
close all;

%% 输入参数
motionParams = struct();
motionParams.dt = 0.001;  %s
motionParams.L = 100;     %mm
motionParams.vs = 0;      %mm/s
motionParams.ve = 0;      %mm/s
motionParams.vc = 100;    %mm/s
motionParams.acc = 1000;  %mm/s^2
motionParams.dec = 1500;  %mm/s^2
smoothFactor = 50; %平滑因子，用于衡量加加速度，非负整数，时间增加smoothFactor*插补周期

%% 梯形速度规划
[motionParams, sta] = trapezoidal_velocity_planning(motionParams);
if sta == 0
    error('当前运动参数下无法规划！');
end

%% 梯形速度插补
count = ceil(motionParams.totalT / motionParams.dt) + 1;
time = zeros(count, 1);
pos = zeros(count, 1);
vel = zeros(count, 1);
acc = zeros(count, 1);
vel(1) = motionParams.vs;
acc(1) = motionParams.acc;
motionParams.t = 0.0;
for i = 2 : count
    motionParams.t = motionParams.t + motionParams.dt;
    [pos(i), vel(i), acc(i)] = main_axis_interpolation_for_trapezoidal_velocity(motionParams);
    time(i) = motionParams.t;
end

%% 方法1：卷积平滑
newPos1 = [pos ; ones(smoothFactor, 1) * pos(end)];
temp = ones(smoothFactor, 1) / smoothFactor;
smoothNewPos1 = my_conv(newPos1, temp);
smoothNewPos1 = smoothNewPos1(1 : length(newPos1));
smoothNewVel1 = diff(smoothNewPos1) / motionParams.dt;
smoothNewAcc1 = diff(smoothNewVel1) / motionParams.dt;

%% 方法2：滑动平滑滤波
newPos2 = [ones(smoothFactor, 1) * pos(1); pos; ones(smoothFactor, 1) * pos(end)];
count = length(pos) + smoothFactor;
smoothNewPos2 = zeros(count, 1);
for i = 1 : count
    smoothNewPos2(i) = mean(newPos2(i : i + smoothFactor));
end
smoothNewVel2 = diff(smoothNewPos2) / motionParams.dt;
smoothNewAcc2 = diff(smoothNewVel2) / motionParams.dt;

%% 绘图验证结果
figure(1);
plot(pos, 'r');
hold on
plot(smoothNewPos1, 'g--');
plot(smoothNewPos2, 'b:');
legend('梯形速度规划', '卷积平滑', '滑动平滑滤波')
grid;
title('位置曲线 [mm]');

figure(2);
plot(vel, 'r');
hold on
plot(smoothNewVel1, 'g--');
plot(smoothNewVel2, 'b:');
legend('梯形速度规划', '卷积平滑', '滑动平滑滤波')
grid;
title('速度曲线 [mm/sec]');

figure(3);
plot(acc, 'r');
hold on
plot(smoothNewAcc1, 'g--');
plot(smoothNewAcc2, 'b:');
legend('梯形速度规划', '卷积平滑', '滑动平滑滤波')
grid;
title('加速度曲线 [mm/sec^2]');

三、总结

  采用梯形速度规划，采用卷积平滑方法和滑动平滑滤波方法均可以很容易生成S形速度曲线。卷积平滑方法不适用于在线插补，滑动平滑滤波方法则适用。两种方法有个缺点是：不适用于起始速度vs和结束速度ve不为0的情况。