CNN基础知识 || softmax与交叉熵

一、函数

1 sigmoid

将一个数值通过函数映射到0-1之间。
sigmoid函数表达式如下
                                                                        
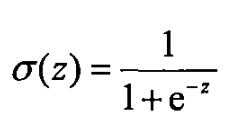
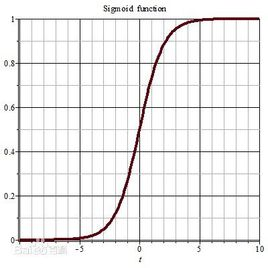
可以看到在趋于正无穷或负无穷时，函数趋近平滑状态，sigmoid函数因为输出范围（0，1），所以二分类的概率常常用这个函数。优点：1.值域在0和1之间；2.函数具有非常好的对称性

2 softmax

将一组数值进行组间的指数归一化

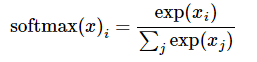
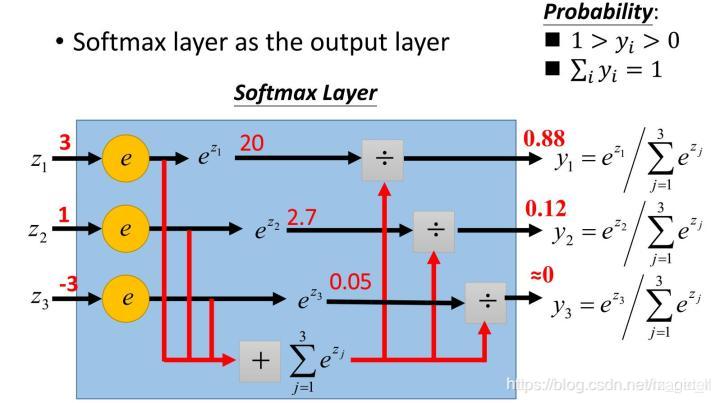
指数函数的值域取值范围是零到正无穷。与概率取值相似的地方是它们都是非负实数。那么我们可以利用指数函数将多分类结果映射到零到正无穷。然后进行归一化处理，便得到了近似的概率。

1. 分子：通过指数函数，将实数输出映射到零到正无穷
2. 分母：将所有结果相加，进行归一化。

二、熵的梳理

1 信息量

首先是信息量。假设我们听到了两件事，分别如下： 
事件A：巴西队进入了2018世界杯决赛圈。 
事件B：中国队进入了2018世界杯决赛圈。 
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

                       
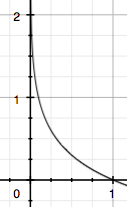
由于是概率所以p(x0)的取值范围是[0,1][0,1],绘制为图形如右图

2 熵（信息量的期望）

考虑另一个问题，对于某个事件，有nn种可能性，每一种可能性都有一个概率p(xi)
这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量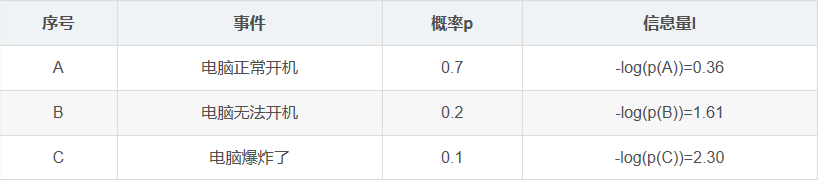

我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：
                                                      

其中n代表所有的n种可能性，所以上面的问题结果就是

                                                 

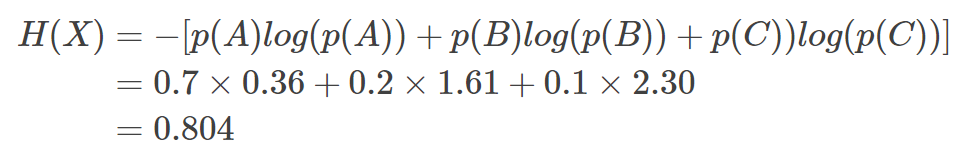
然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式
                                                    

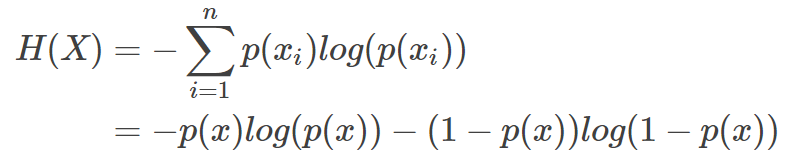
3 相对熵

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1] 。
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。KL散度的计算公式：

                                                            
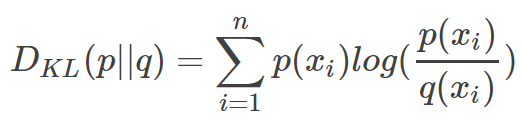
n为事件的所有可能性。
Dkl的值越小，表示q分布和p分布越接近。

4 交叉熵

对上面的式子进行形变得到：

                                                         

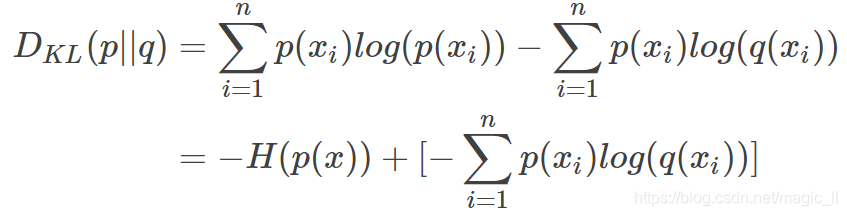
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

                                                                

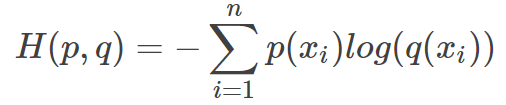
在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即DKL(y||y^)DKL(y||y^)，由于KL散度中的前一部分−H(y)−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

三、机器学习中交叉熵的应用

1.为什么使用交叉熵

在线性回归问题中，常使用到MSE（Mean Squared Error）作为loss函数，比如：
                                                   

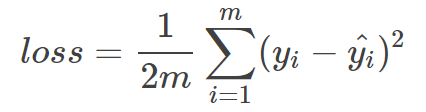
这里的m表示m个样本，loss为m给我样本的loss均值
MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么

2 交叉熵在一对一分类问题中的使用

这里的一对一是指，每一张图像样本只能有一个类别，比如只能是狗或者只能是猫。
交叉熵在一对一问题上基本是标配的方法

                                                    

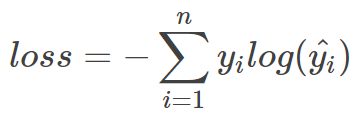
上式为一张样本的loss计算方法。式2.1中n代表着n种类别。

举例说明,比如有如下样本：

对应的标签和预测值
（网络的预测向量的和并不为1，一对一要求所有的概率和为1。所以网络最后一层要经过softmax，进行指数归一化，转成和为1的向量）

那么有

                             

对应的一个batch的loss就是
                               
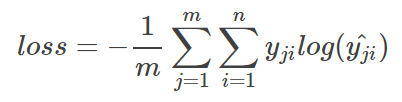
m为当前batch的样本数

3 交叉熵在一对多分类问题中的使用

这里是指每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗。
比如下面这张样本图，即有青蛙，又有老鼠，所以是一对多的分类问题

对应的标签和预测值
（网络的预测向量的每个值并不在0-1之间，一对多要求所有的概率处于0-1之间。所以网络最后一层要经过sigmoid，进行转换，保证每个值都在0-1之间）

对于预测向量的每一个值，我们可以看成是二分类的问题，交叉熵可以简化成

                                               

注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。
例子中可以计算为：

                                     

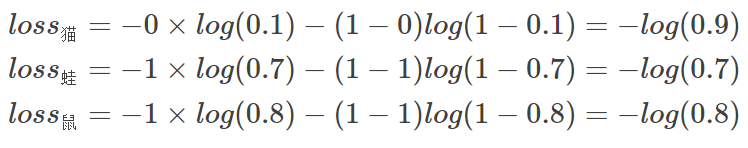
单张样本的loss即为
每一个batch的loss就是：

                                         

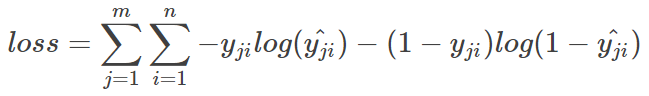
式中m为当前batch中的样本量，n为类别数4

4 softmax和cross-entropy的关系

softmax是计算概率分布。cross-entropy是计算两个概率分布的相似性。求概率分布的方式和损失函数之间没有必然的联系。是在神经网络当中，经常会用softmax函数计算概率，然后再用cross-entropy计算损失值。

 

四 tensorflow中的使用

1 softmax_cross_entropy_with_logits
与 sparse_softmax_cross_entropy_with_logits

(用在一对一的分类的网络中）

(1) 在计算loss的时候，最常见的就是softmax_cross_entropy_with_logits

loss = tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)
loss = tf.reduce_mean(loss)

• 参数logits：神经网络最后一层的输出，如有batch，它的大小为[batchsize, num_classes]，类型为 float16/32/64
• 参数labels：实际的标签，大小类型和logits保持一致

 等价于

y = tf.nn.softmax(logits)                   
cross_entropy = -y_*tf.log(y)               #向量
loss = tf.reduce_sum(cross_entropy)         #值

• 网络的输出是向量，要先进行softmax（转换成概率）然后计算交叉熵（label的概率和预测的概率的分布的差异)

(2) sparse_softmax_cross_entropy_with_logits

label = [0,1,3,2]
logits = tf.convert_to_tensor([[1.0,2.0,3.0], [1.0, 2.0, 3.0],[1.0,2.0,3.0]])   #our NN's output
cross_entropy = tf.reduce_sum(tf.nn.sparse_softmax_cross_entropy_with_logits(labels=label,logits=logits))

• label：元素的类型为int，大小为[batch]
• logits：网络的输出。元素为tf.float，大小为[batch, num_classes]

栗子

import tensorflow as tf

label_or = [0,2,1]
label = tf.cast(label_or, tf.int32)
label = tf.one_hot(label, 3, 1, 0, axis=0)       #3:分3类，类别位置为1，其余为0，
label = tf.to_float(label)
# label = [[1 0 0 0], [0 0 1 0], [0 1 0 0]]      #true label

a = [[1.0,2.0,3.0], [1.0, 2.0, 3.0],[1.0,2.0,3.0]]
logits = tf.convert_to_tensor(a)   #our NN's output

y = tf.nn.softmax(logits)                          # 默认axis = -1
# predicts = tf.argmax(y, axis=-1, name='predicts')  # 预测时候使用
  
cross_entropy = -tf.reduce_sum(label*tf.log(y))   #不推荐。当a的元素过大，自己写的交叉熵计算会失败
cross_entropy2 = tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(labels=label, logits=logits))
cross_entropy3 = tf.reduce_sum(tf.nn.sparse_softmax_cross_entropy_with_logits(labels=label_or,logits = logits))  #label_or必须在0-(n-1)之间，n为分类数量

with tf.Session() as sess:
    print('step1: softmax is:',sess.run(y))
    print('softmax method 1 is:', sess.run(cross_entropy))
    print('softmax method 2 is:',sess.run(cross_entropy2))
    print('softmax method 3 is:',sess.run(cross_entropy3))

softmax的计算与数值稳定性

在Python中，softmax函数为：

def softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x)

# 传入数值较小时
softmax([1, 2, 3, 4, 5])
# array([ 0.01165623,  0.03168492,  0.08612854,  0.23412166,  0.63640865])

# 传入数值较大时
softmax([1000, 2000, 3000, 4000, 5000])
# array([ nan,  nan,  nan,  nan,  nan])

这是因为在求exp(x)时候溢出了：

import math
math.exp(1000)
# Traceback (most recent call last):
#   File "<stdin>", line 1, in <module>
# OverflowError: math range error

一种简单有效避免该问题的方法就是让exp(x)中的x值不要那么大或那么小，在softmax函数的分式上下分别乘以一个非零常数：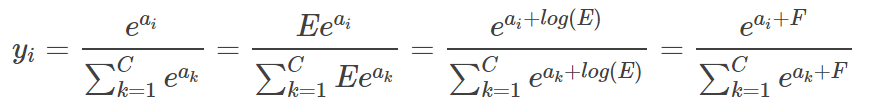 

这样做相当于

def softmax(x):
    shift_x = x - np.max(x)   #[1000, 2000, 3000, 4000, 5000]==>>[-4000,-3000,-2000,-1000,0]
    exp_x = np.exp(shift_x)
    return exp_x / np.sum(exp_x)

a = softmax([1000, 2000, 3000, 4000, 5000])
# array([ 0.,  0.,  0.,  0.,  1.])

这样也是有问题的：softmax函数不可能产生0值，但这总比出现nan的结果好，并且真实的结果也是非常接近0的。

在tensorflow中tf.nn.softmax和tf.nn.softmax_cross_entropy_with_logits等都将这个滑动操作添加。自己写交叉熵时，输入元素较大时得到的输出元素中出现为0，计算tf.log会失败。

2 sigmoid_cross_entropy_with_logits

（用在一对多分类的网络中）
用法和softmax_cross_entropy_with_logits基本一样，原理有所差别