Codeforces Round #698 (Div. 1) D. Nezzar and Hidden Permutations（高难度的构造问题）

最新推荐文章于 2025-01-20 09:00:00 发布

madaidao

最新推荐文章于 2025-01-20 09:00:00 发布

阅读量278

点赞数

分类专栏：构造图论文章标签：算法

本文链接：https://blog.youkuaiyun.com/madaidao/article/details/114098899

版权

图论同时被 2 个专栏收录

34 篇文章

订阅专栏

构造

4 篇文章

订阅专栏

给定整数n和m，以及m对不重复的数字，找到两个1到n的排列p和q，使得对于所有选出的数字对(l, r)，p_l - p_r和q_l - q_r具有相同的符号，并使满足p_i != q_i的i的数量最大化。解决方案涉及将问题转化为图论问题，通过构造特定的树形结构来找到满足条件的排列。" 114255333,10536229,Java FTP 实现跨服务器文件操作,"['Java', 'FTP', '文件操作', '服务器管理']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://codeforces.com/contest/1477/problem/D

D. Nezzar and Hidden Permutations

time limit per test

5 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Nezzar designs a brand new game "Hidden Permutations" and shares it with his best friend, Nanako.

At the beginning of the game, Nanako and Nezzar both know integers nn and mm. The game goes in the following way:

Firstly, Nezzar hides two permutations p1,p2,…,pnp1,p2,…,pn and q1,q2,…,qnq1,q2,…,qn of integers from 11 to nn, and Nanako secretly selects mm unordered pairs (l1,r1),(l2,r2),…,(lm,rm)(l1,r1),(l2,r2),…,(lm,rm);
After that, Nanako sends his chosen pairs to Nezzar;
On receiving those mm unordered pairs, Nezzar checks if there exists 1≤i≤m1≤i≤m, such that (pli−pri)(pli−pri) and (qli−qri)(qli−qri) have different signs. If so, Nezzar instantly loses the game and gets a score of −1−1. Otherwise, the score Nezzar gets is equal to the number of indices 1≤i≤n1≤i≤n such that pi≠qipi≠qi.

However, Nezzar accidentally knows Nanako's unordered pairs and decides to take advantage of them. Please help Nezzar find out two permutations pp and qq such that the score is maximized.

Input

The first line contains a single integer tt (1≤t≤5⋅1051≤t≤5⋅105) — the number of test cases.

The first line of each test case contains two integers n,mn,m (1≤n≤5⋅105,0≤m≤min(n(n−1)2,5⋅105)1≤n≤5⋅105,0≤m≤min(n(n−1)2,5⋅105)).

Then mm lines follow, ii-th of them contains two integers li,rili,ri (1≤li,ri≤n1≤li,ri≤n, li≠rili≠ri), describing the ii-th unordered pair Nanako chooses. It is guaranteed that all mm unordered pairs are distinct.

It is guaranteed that the sum of nn for all test cases does not exceed 5⋅1055⋅105, and the sum of mm for all test cases does not exceed 5⋅1055⋅105.

Output

For each test case, print two permutations p1,p2,…,pnp1,p2,…,pn and q1,q2,…,qnq1,q2,…,qn such that the score Nezzar gets is maximized.

Example

input

Copy

output

Copy

1 2 3 4
3 4 1 2
2 3 4 1 6 5
1 4 3 2 5 6
1 2
1 2

Note

For first test case, for each pair given by Nanako:

for the first pair (1,2)(1,2): p1−p2=1−2=−1p1−p2=1−2=−1, q1−q2=3−4=−1q1−q2=3−4=−1, they have the same sign;
for the second pair (3,4)(3,4): p3−p4=3−4=−1p3−p4=3−4=−1, q3−q4=1−2=−1q3−q4=1−2=−1, they have the same sign.

As Nezzar does not lose instantly, Nezzar gains the score of 44 as pi≠qipi≠qi for all 1≤i≤41≤i≤4. Obviously, it is the maximum possible score Nezzar can get.

题目大意：给定两个数字 n,m 。

以及m对数字，,m对数不重复出现

求出两个1到n的排列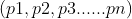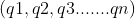， (p1,p2,p3......pn) ， (q1,q2,q3.......qn) ，对于所有要求和符号相同，并且对于所有，要让满足的数目最大。

题解：我们可以把问题抽象到图上，构造一个图，包含n个编号为1到n的点，对于每对，我们在点和点之间建一条边。我们需要在每个点上填两个数字和，若点和点之间存在一条边，则点和点上的数字之间的大小关系和数字之间的大小关系相同。n个点上的数字和，分别合在一起，均为数字1到n的排列。

观察这个图，若某个点的度数为n-1，则这个点上 p==q ，我们可以把剩下的任意数填到这些点上。我们可以去掉这些点，继续解决问题。

对于剩下的点，我们再构造一个图，若图中点和之间不存在一条边，则在图中点和点之间存在边。图中，若两个点存在边，则两个点之间填的数字互不影响。如何在图上构造问题的解呢？

我们观察图的生成树，若为星形树，我们设星形树的中心为，叶子节点为 v1,v2,v3....vk ，那么我们可以这样构造树上的数字：

这样每个点上的和都不相同。

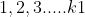若图的生成树不为星形树，我们可以把生成树分割为多个星形树，我们可以把 1,2,3.....k1 分配到大小为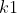的生成树，把 k1+1,k1+2,k1+3....,k1+k2 分配到大小为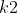的生成树，依次类推，这样生成树之间数字的大小关系也是满足条件的。

例如下图就被分割为三个星形树：

接下来的问题是如何将树分割为多个星形树。算法有多种。

例如：遍历每一个点，若点的相邻点也未被纳入星形树，则让点做树的中心，点做树的叶子节点。若没有为纳入星形树的相邻节点，则任意选择一个相邻的点，若点v为树心，则将点纳入点的星形树；若点为叶子节点，且所在的星形树有多个叶子节点，则把点从原来的星形树中删除，点和点合并为一个星形树。若点为叶子节点，且所在的星形树只有一个叶子节点，则让点做原树的树心，点做点的叶子节点。这个算法每个点都一定可以纳入一个星形树。

例如：我们可以递归分割生成树，把树的所有叶子节点和其父节点分割为一个星形树。剩下的点按照同样的算法继续递归分割，若最后剩下树的根节点未纳入星形树，则将其纳入任意一个子节点的生成树即可。

求出生成树并分割为星形树的复杂度为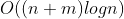 O((n+m)logn)

本题的建图以及分割和构造的思路实在是十分巧妙！

代码如下：

#include<bits/stdc++.h>

using namespace std;
const int nn =510000;
const int inff = 0x3fffffff;
const double eps = 1e-8;
typedef long long LL;
const double pi = acos(-1.0);
const LL mod = (479 << 21) + 1;
int n,m;
int l[nn],r[nn];
int degree[nn];
set<int> G[nn]; //原图
set<int> rv;
set<int> T[nn]; //生成树
void dfs(int u)
{
    rv.erase(u);
    int v=0;
    while(rv.size())
    {
        auto iter = rv.upper_bound(v);
        if(iter==rv.end())
            break;
        v = *iter;
        if(G[u].find(v)!=G[u].end()) continue;
        T[u].insert(v);
        T[v].insert(u);
        dfs(v);
    }
}
struct Star
{
    int center;
    set<int> son;
};
vector<Star> vecstar;
int inStar[nn];
int p[nn],q[nn];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
        {
            degree[i]=0;
            inStar[i]=-1;
        }
        rv.clear();
        vecstar.clear();
        for(int i=1;i<=m;i++)
        {
            cin>>l[i]>>r[i];
            degree[l[i]]++;
            degree[r[i]]++;
            G[l[i]].insert(r[i]);
            G[r[i]].insert(l[i]);
        }
        for(int i=1;i<=n;i++)
        {
            if(degree[i]!=n-1)
            {
                rv.insert(i);
            }
        }
        while(rv.size())
        {
            auto iter = rv.begin();
            dfs(*iter);
        }
        for(int i=1;i<=n;i++)
        {
            if(inStar[i]!=-1)
                continue;
            Star s;
            for(auto it = T[i].begin();it!= T[i].end();it++)
            {
                int v=*it;
                if(inStar[v]==-1)
                {
                    s.son.insert(v);
                    inStar[v]=int(vecstar.size());
                }
            }
            if(s.son.size())
            {
                s.center = i;
                inStar[i] = int(vecstar.size());
                vecstar.push_back(s);
            } else {
                auto it = T[i].begin();
                if(it==T[i].end())
                {
                    s.center = i;
                    inStar[i] = int(vecstar.size());
                    vecstar.push_back(s);
                } else {
                    int v=*it;
                    Star &vStar = vecstar[inStar[v]];
                    if(vStar.center == v)
                    {
                        vStar.son.insert(i);
                        inStar[i] = inStar[v];
                    } else if(vStar.son.size()>1){
                        vStar.son.erase(v);
                        s.center = i;
                        s.son.insert(v);
                        inStar[v] = int(vecstar.size());
                        inStar[i] = int(vecstar.size());
                        vecstar.push_back(s);
                    } else {
                        vStar.son.erase(v);
                        vStar.son.insert(vStar.center);
                        vStar.son.insert(i);
                        inStar[i]=inStar[v];
                        vStar.center = v;
                    }
                }
            }
        }
        int num=1;
        for(int i=0;i<int(vecstar.size());i++)
        {
            Star &s = vecstar[i];
            if(s.son.size()==0)
            {
                p[s.center]=q[s.center]=num;
                num++;
                continue;
            } else {
                p[s.center] = num;
                q[s.center] = num+int(s.son.size());
                int i=0;
                for(auto it = s.son.begin();it!=s.son.end();it++)
                {
                    i++;
                    int v=*it;
                    p[v] = num+i;
                    q[v] = num+i-1;
                }
                num+=i+1;
            }
        }
        for(int i=1;i<=n;i++)
            cout<<p[i]<<" ";
        cout<<endl;
        for(int i=1;i<=n;i++)
            cout<<q[i]<<" ";
        cout<<endl;
        for(int i=1;i<=n;i++)
        {
            T[i].clear();
            G[i].clear();
        }
    }
    return 0;
}