1. 概述
导读:这篇文章是对于检测网络训练过程中存在的问题进行了分析,分析明确指出检测网络在训练过程中会存在明显的不平衡问题,这里的不平衡问题大体分为3个层次:检测框采样机制层次、特征图层次、目标函数层次。对此,文章对于这些不同层次的不平衡问题进行了研究,并对每个层次的问题提出了对应的解决办法,这也是文章对应的创新点,它们分别是IoU-balanced sampling、balanced feature Pyramid以及balanced L1 loss。对于改进之后的检测器取名为Libra RCNN,其在MSCOCO数据集上相比带FPN的Faster RCNN以及RetinaNet分别提升了2.5与2个点的mAP。对应的代码已经merge到了mmdetection中了。
对于一个目标检测器训练其训练结果良好与否(充分发挥检测器的性能)有三个关键方面:
- 1)检测器对于检测框的选择是否具有代表性;
- 2)检测器从输入图像抽取出来的特征是否被完全利用;
- 3)检测器设计的损失函数是否最最优的;
以上的3点也是文章中进行分析的,也给出了对应的解决方法。其中对于上面提到的三个问题,可以对其进行简要的分析。
区域采样层次的不平衡
在检测其中困难样本是对提升检测器的性能极具价值的,但是在传统的随机采样过程中会导致采样集合中的简单样本占据大多数,如下图所示:

对应的解决办法有OHEM与Focal Loss。首先对于OHEM其可以选择出按照检测框的loss选择出困难样本,但是这样的代价是较大的计算量与内存占用问题,而且这个方法对噪声并不鲁棒;Focal Loss在一阶段检测方法中被证明是很有效的,但是在两阶段的检测方法中收效是很小的,这是由于在RPN阶段就滤除掉了很多的负样本。
特征层次上的不平衡
为了对不同尺度的目标提供更好的适配,往往在检测网络中引入FPN类型的网络结构,实际也是证明将高低层次的信息互补会带来检测性能的提升。但是这些信息是被有效使用了么?对此文章进一步提升了对应部分的特征表达,提出了balanced Pyramid。
损失函数层次上的不平衡
检测器会存在两部分的损失:分类和边界框回归,一般这两部分的损失是如下图中的分布:

这样的分布自然是不对等的,文章对此进行了研究,对检测框的损失函数在smooth L1的基础上进行调整得到balanced L1损失函数。
2. 方法
2.1 网络结构
文章的网络结构见下图所示:

对应的三处改进在下面的内容中分开进行说明。
2.2 IoU balanced sampling
在下图中展示了不同采样方法中不同IoU框的分布情况:

蓝色的条是随机采样的结果,由于原始采样空间中IoU低的占了大部分,自然随机采样的结果其也是占了绝大部分(70%)。在使用OHEM(橘黄色的条)之后样本的分布变化有了明显变化,大于0.05的框占到了60%,但是OHEM带来的问题也在前面分析过了,对此文章提出了IoU-Balanced Sampling的采样方法,这个方法更加简洁有效。
在随机采样过程中对于需要在数量为MMM的集合中选择NNN个困难样本,这每个困难样本被选择到的概率就是:
p=NMp=\frac{N}{M}p=MN
而现在文章对此进行了改进,将原始的采样集合划分为KKK个区间,每个区间的候选样本数量为MkM_kMk,还是假设总的采样数目不变,则采样的概率就变成了:
pk=NK∗1Mk,k∈[1,K)p_k=\frac{N}{K}*\frac{1}{M_k},k\in [1, K)pk=KN∗Mk1,k∈[1,K)
通过这样的方式改变了原有采样的分布,并且实现简单,效果也很不错。其中KKK的选择对应性能的影响见下表所示:
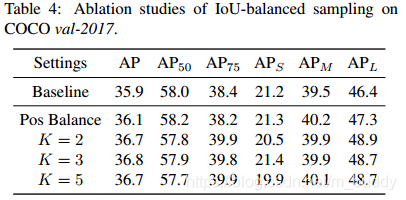
2.3 Balanced Feature Pyramid
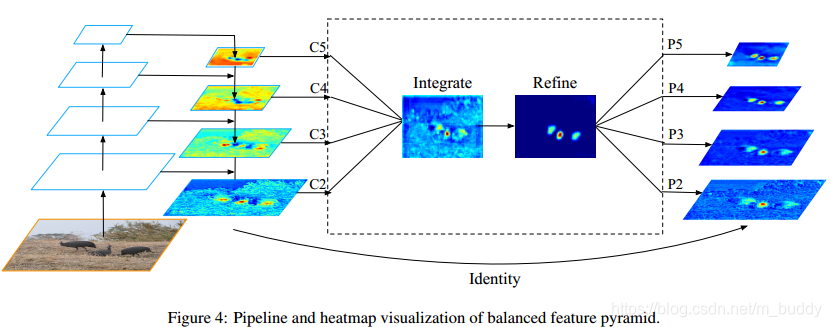
文中说到的feature level的不平衡表现在高低 level特征的利用上,如何利用不同分辨率的特征,文中将其分为了四步:rescaling,integrating,refining,strengthening。
rescaling & integrating
对于FPN的特征金字塔其特征用{C2,C3,C4,C5}\{C_2,C_3,C_4,C_5\}{C2,C3,C4,C5}进行表示,它们的分辨率依次减小,而这些特征中表达是存在差异的,文中是利用上图中结构将这些特征进行整合,从而起到丰富与平衡特征的目的。例如,以C4C_4C4作为基准,那么其它的层就进行插值与最大值池化归一化到C4C_4C4对应的尺寸上来,然后再做简单的相加取平均操作:
C=1L∑l=lminlmaxClC=\frac{1}{L}\sum_{l=l_{min}}^{l_{max}}C_lC=L1l=lmin∑lmaxCl
就是这样简单的操作并没有引入什么超参数就可以实现,最终在AP上也得到了验证是有效的。
refining & strengthening
rescaling后取平均提取到的的特征还可以进一步地refine成更discriminative,作者这里用到了non-local模块,paper中使用了Gaussian non-local attention增强integrate后的特征。
2.4 Balanced L1 Loss
在检测网络中网络的损失由两个部分组成:分类损失、边界框损失,它们通过参数λ\lambdaλ进行调整,一般来讲分类的损失是大于边界的损失的。那么为了平衡的话比较直观的方法就是调整λ\lambdaλ的值,但是这样会影响文章说的outlier(可以理解为困难样本)带来的梯度值,因为这些值本来就很大,这样就会导致训练过程的不稳定。而对于inlier(可以理解为简单样本)其梯度值只占到总梯度的30%,对此文章对原本的Smooth L1损失函数进行了改进。改进思想就是将原来的斜线部分掰弯,其曲线图为:
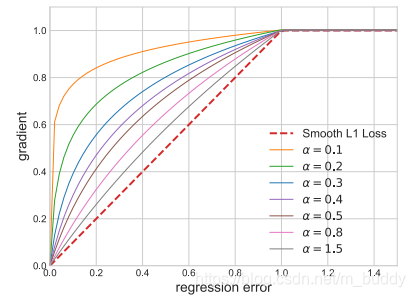
对应的设计出来的梯度函数为:
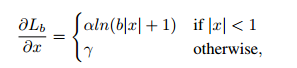
其中,α\alphaα控制inlier的梯度幅度,γ\gammaγ控制outlier,那么由梯度的公式那么就可以反推得到原始的函数形式:
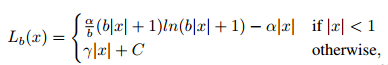
其中还有几个参数需要满足如下的关系:
α∗ln(b+1)=γ\alpha*ln(b+1)=\gammaα∗ln(b+1)=γ
在文中将上面涉及到的参数设置为:α=0.5\alpha=0.5α=0.5,γ=1.5\gamma=1.5γ=1.5,b=eγαb=e^{\frac{\gamma}{\alpha}}b=eαγ。
3. 实验结果
性能比较:
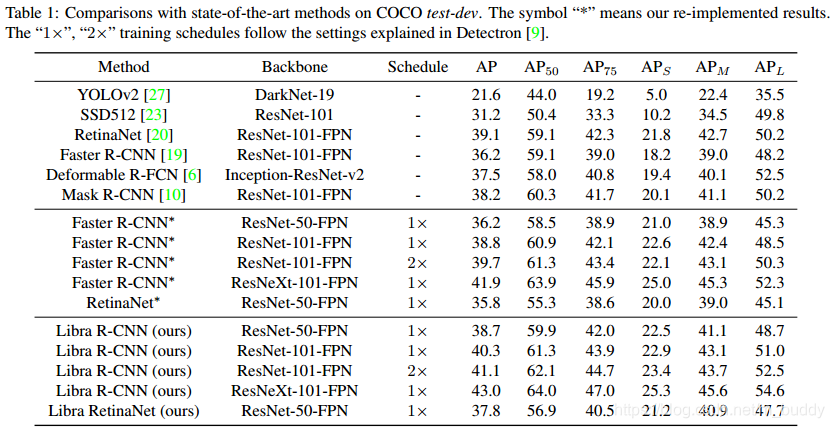
文中提到的改进对性能带来的影响:






 本文分析了目标检测网络训练中的不平衡问题,包括采样、特征利用和损失函数三个方面,并提出了解决方案:IoU平衡采样、平衡特征金字塔和平衡L1损失。通过这些改进,Libra RCNN在MSCOCO数据集上提高了性能。
本文分析了目标检测网络训练中的不平衡问题,包括采样、特征利用和损失函数三个方面,并提出了解决方案:IoU平衡采样、平衡特征金字塔和平衡L1损失。通过这些改进,Libra RCNN在MSCOCO数据集上提高了性能。
















 879
879

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








