机器学习————决策树

一、决策树概述

1.1概述

  决策树是一种非参数的监督学习方法，通过对训练集数据学习，挖掘一定规则用于对新的数据集进行预测，通俗来说，是if-then决策集合。目的是使样本尽可能属于同一类别，分类更准确，通过递归选择最优特征对数据集进行分割，使每个子集都有一个最优分类过程。通过特征选择，选择最佳特征，将数据集分割成正确分类的子集。
常用的特征选择及对应算法：
信息增益——ID3算法
信息增益率——C4.5算法
基尼系数——CART算法

三种算法比较： 

算法	模型	连续值	缺少值
ID3	分类	不支持	不支持
C4.5	分类	支持	支持
CART	分类回归	支持	支持

1.1.1 ID3算法

基于信息增益为度量指标的分类算法，用到了熵理论，熵越小信息越纯，效果越好，选取熵值小（信息增益大）作为分类节点

一般步骤如下：

假设数据集D，|D|表示样本总个数，数据集有K个分类，记为Ck，特征A有j个不同取值{a1,……,aj}
由A可以把D分为j个子集
Dik为子集D再按k划分而得的子集

已知：

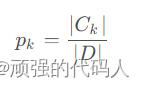
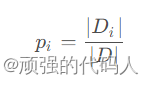
①因此总信息熵为

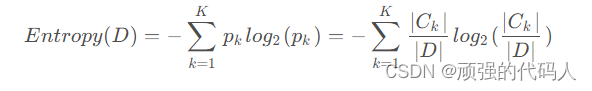
②特征条件下经验条件熵

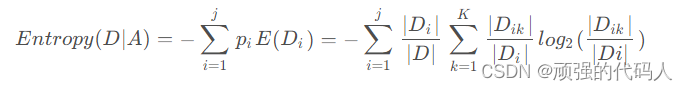
③特征的信息增益

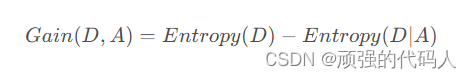
④进行①-③计算每个点的信息增益，选择值最大的进行扩展

⑤重复①-④直到叶子节点唯一即建立决策树

1.1.2 C4.5算法

基于信息增益率作为指标，在ID3基础上能处理连续型数据，也能处理有缺失情况的数据集。
在ID3的①-③步中额外新增两步:

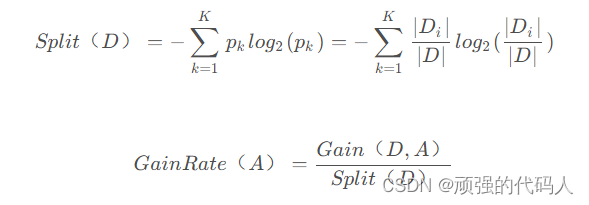
选择最大信息增益率作为分裂节点

1.1.3 CART算法

基于Gini系数的分类回归算法，选择Gini系数小的作为分裂节点
①计算总Gini系数

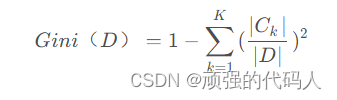
②计算每个特征变量的Gini系数（可能因此分为D1、D2两部分）

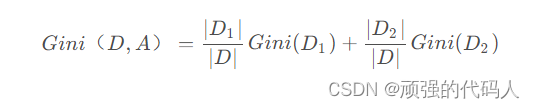
③选择Gini系数最小的作为分裂节点

连续型：
将连续值离散化，将值按序划分，m个值就有m-1种划分方式，分为D1.D2.计算每种划分下的Gini系数，选最小的作为最终结果

离散型（文本）：
一个值为D1，另外一个值为D2，计算Gini系数，选最小的结果

1.2 实现

1.2.1 数据集介绍

数据集采用周志华《机器学习》课后习题4.3的西瓜数据集