机器学习————SVM

最新推荐文章于 2024-06-10 22:14:37 发布
原创 最新推荐文章于 2024-06-10 22:14:37 发布 · 799 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#支持向量机 #机器学习 #算法

目录

一、SVM

1.1 概述

1.2 四种分隔的情况

1.3 最大间隔与分类

1.4 对偶问题：等式约束

1.5 核函数

二、实现

2.1 数据集介绍

2.2 代码

2.2.1 数据可视化部分

2.2.2 SMO实现

2.2.3 结果

三、总结

一、SVM

1.1 概述

支持向量机（Support Vector Machine，简称SVM）是一种经典的机器学习算法，它在解决小样本、非线性及高维模式识别等问题中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。
是一种二分类模型，监督性学习。目的是找到集合边缘上的若干数据（支持向量）用这些点找出一个平面（决策面）使支持向量到该平面的距离最大。

1.2 四种分隔的情况

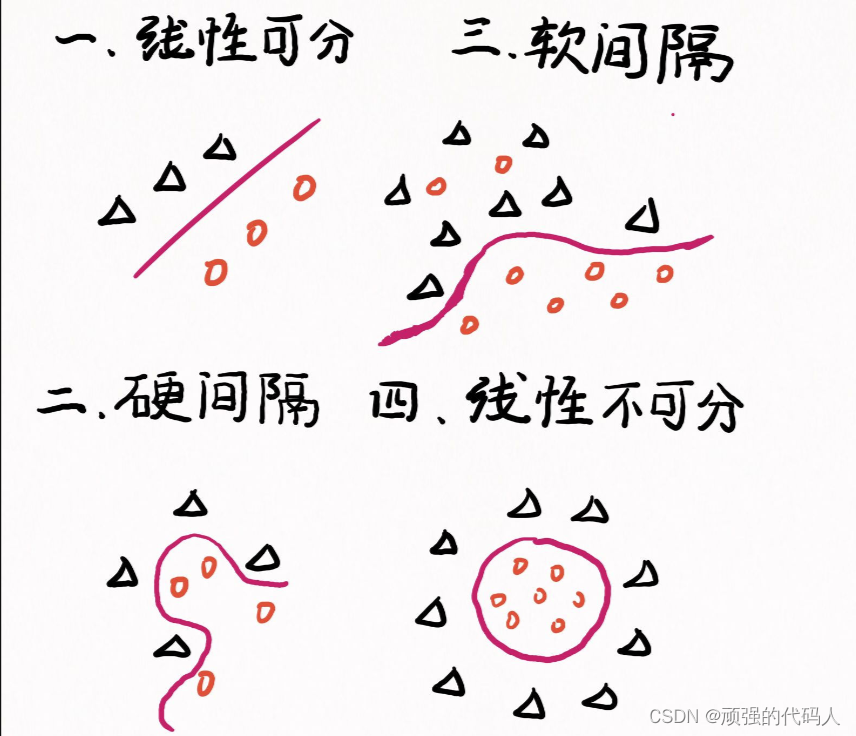
此外，我们将详细介绍一些线性可分的情况

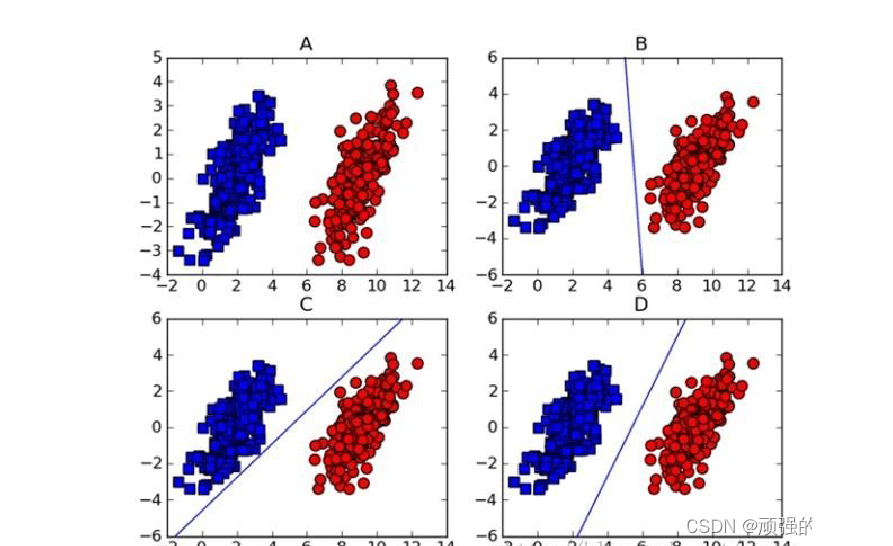
如上图所示，在图A中的两组数据已经分的足够开，因此很容易就可以画一条直线将两组数据点分开。
这种情况下，这组数据就被称为线性可分数据。

将数据集分开的直线称为分割超平面。当数据点都在二维平面上时，分割超平面只是一条直线。当数据集是三维时就是一个平面。如果数据集是N维的，那么就需要N-1维的某某对象对数据进行分割。该对象就被称为超平面也是分类的决策边界。

根据这种方法我们构造一个分类器，如果数据点离决策边界越远，那么其最后的预测结果也就越可信

点到分割线的距离称为间隔
而支持向量就是离分隔超平面最近的那些点。

1.3 最大间隔与分类

什么样的决策边界才是最好的呢？
首先我们引入
超平面方程：

w^Tx+b=0

对于线性可分的数据集来说，超平面有许多个，但几何间隔最大的分离超平面是唯一的。
① 两类样本分别分割在超平面的两侧
② 两侧距离超平面最近的样本点到超平面的距离被最大化

点

x=(x_1,x_2,\ldots\ldots x_n)

到直线

w^Tx+b=0

距离为

\frac{(w^Tx+b)}{||w||}

其中

||w||=\sqrt{w_1^2+\ldots\ldots+w_n^2}

\begin{cases}&\frac{(w^Tx+b)}{||w||}\geq d,y=1\\&\frac{(w^Tx+b)}{||w||}\leq-d,y=-1\end{cases}

支持向量（正、负）之差为

\frac2{||w||}

则最大间隔转化为求其最大值

arg\max_{w,b}\frac2{||w||}

即

最低0.47元/天 解锁文章
SVM——支持向量机的学习入门
君一席
09-14 1658
SVM算法的基本原理，包括硬间隔和软间隔的概念，以及在处理线性和非线性分类、回归和异常值检测中的应用。通过Scikit-Learn示例，展示了SVM在实际项目中的操作，并探讨了SVM的优点和选择核函数的策略。
机器学习：支持向量机（SVM）
m0_63698246的博客
12-18 1502
支持向量机（Support Vector Machine，SVM）是一种常用的监督学习算法，用于分类和回归任务。SVM的基本原理是构建一个最优超平面来分割不同类别的数据点。在二分类问题中，SVM试图找到一个能够将两个类别的数据点尽可能分开的超平面。超平面是一个d-1维的线性子空间，其中d是数据的特征维度。SVM的目标是找到具有最大间隔（即离超平面最近的样本点的距离最大）的超平面。SVM的核心思想是将数据映射到高维特征空间中，通过引入核函数可以避免直接计算高维特征空间的复杂性。
SVM学习教程(自己学习时候看的PDF)
10-23
学习SVM时候找了很多资料最终选择的这个PDF一看就懂了
SVM学习总结
热门推荐
MyArrow的专栏
04-27 2万+
1. 目标      SVM是一个二类分类器，它的目标是找到一个超平面，使用两类数据离超平面越远越好，从而对新的数据分类更准确，即此分类器更加健壮。      支持向量（Support Vetor）：就是离分隔超平面最近的哪些点。      寻找最大间隔：就是寻找最大化支持向量到分隔超平面的距离，在此条件下求出分隔超平面。      数据分类类别：      1）线性可分      2
svm学习
cschengvdn3的专栏
09-25 1007
Libsvm学习 一  运行   wang@linux:~/test/libsvm-2.84>./svm-train heart_scale * optimization finished, #iter =162 nu = 0.431029 obj = -100.877288, rho =0.424462 nSV = 132, nBSV = 107 Total nSV = 132
机器学习——SVM，微博不实信息分类
06-24
利用支持向量机对于微博爬取的不实信息进行分类，并且爬取正常的微博信息，判断微博是否不实。其中正常微博为0，不实微博为1
精选资源
OpenCV机器学习——支持向量机SVM
01-27
OpenCV中集成了多种机器学习算法供我们方便使用，如果我们要训练数据进行分类，不用自己写分类器，只需要调用相应的库和类即可轻松实现。本文重点不在于介绍机器学习原理及数学推导，着重介绍OpenCV中的机器学习相关...
精选资源
机器学习——支持向量机SVM算法完整实战源码
05-16
基于Python和sklearn机器学习库实现的支持向量机算法使用的实战案例。 使用jupyter notebook环境开发。 支持向量机：支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据...
机器学习——svm
hh3023241040的博客
06-10 1819
1.1 支持向量机SVM（支持向量机）是一种常见的监督学习算法，用于分类和回归问题。在分类问题中，SVM通过在特征空间中找到一个最优的超平面来将不同类别的数据分隔开。在回归问题中，SVM通过寻找一个最优的超平面来拟合数据点，使得尽可能多的数据点位于超平面的边界上。SVM的核心思想是将原始特征映射到一个高维特征空间，并在该空间中找到一个最优的超平面。为了找到最优的超平面，SVM采用了两个关键概念：间隔和支持向量。间隔表示超平面到最近的训练样本的距离，SVM的目标是找到具有最大间隔的超平面。
python机器学习入门案例——基于SVM分类器的鸢尾花分类（附完整代码）
12-21
在本文中，我们将探讨Python机器学习的一个入门案例，特别是如何使用支持向量机（SVM）分类器对鸢尾花数据集进行分类。这个案例涵盖了数据预处理、模型构建、训练以及性能评估。 首先，鸢尾花数据集是机器学习领域...
SVM在RGB图像分割中的应用
03-22
基于SVM的RBG图像分割，对图像的前景与后景进行分割
SVM 学习
s1162276945的博客
07-19 310
SVM是Support Vector Machines（支持向量机）的缩写，可以用来做分类和回归。 SVC是SVM的一种Type，是用来的做分类的。 SVR是SVM的另一种Type，是用来的做回归的。 SVM多分类 SVMs(Surport Vector Machines)是用来解决两分类问题的，直接用SVMs实现多分类是不行的，只能使用下面这些间接的方法： （1）1-v-r，即对于每一...
SVM学习
Heyuhangxing的博客
08-27 352
目录 SVM基本概念 线性分类与非线性分类 线性分类 非线性分类 拉格朗日乘算法 等式约束 不等式约束 对偶问题 KKT条件 核函数 SMO算法 实例：线性基础 实例：线性展示图 SVM基本概念 SVM理解图： SVM：支持向量机，因其英文名为supportvectormachine，故一般简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。 ...
机器学习（七）——SVM
qq_61179907的博客
12-06 1091
支持向量机（Support Vector Machine，简称SVM）是一种经典的机器学习算法，它在解决小样本非线性及高维模式识别等问题中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。是一种二分类模型监督性学习。目的是找到集合边缘上的若干数据（支持向量）用这些点找出一个平面（决策面）使支持向量到该平面的距离最大。
学习SVM，这篇文章就够了！（附详细代码）
披风秃头侠的博客
04-01 5610
学习SVM，这篇文章就够了！（附详细代码） 支持向量机（SVM），一个神秘而众知的名字，在其出来就受到了莫大的追捧，号称最优秀的分类算法之一，以其简单的理论构造了复杂的算法，又以其简单的用法实现了复杂的问题，不得不说确实完美。 本系列旨在以基础化的过程，实例化的形式一探SVM的究竟。曾经也只用过集成化的SVM软件包，效果确实好。因为众人皆说原理复杂就对其原理却没怎么研究，最近...
深度学习——SVM
m0_64002592的博客
08-20 1774
比如下图中两条虚线构成的带状区域就是 margin，虚线是由距离中央实线最近的两个点所确定出来的（也就是由支持向量决定）。对于线性可分的数据集来说，这样的超平面有无穷多个(即感知机)，但是几何间隔最大的分离超平面却是唯一的。所以在原有目标的基础之上，我们也尽可能的让ξ的总量也尽可能地小。比较好的划分超平面，样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。其中的C是用于控制“最大化间隔”和“保证大部分的点的函数间隔都小于1”这两个目标的权重。为样本的中的一个点，其中。
机器学习SVM——手写数字识别
最新发布
12-31
### 使用支持向量机（SVM）进行手写数字识别 #### 加载必要的库 为了实现手写数字识别，首先需要导入所需的 Python 库。这些库提供了数据处理、模型训练以及评估等功能。 ```python from sklearn import datasets,...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值