Java—方法递归—汉诺塔问题

小元进大厂

已于 2022-06-24 16:51:15 修改

阅读量264

点赞数

分类专栏： Java学习笔记文章标签： java jvm servlet

于 2022-06-24 16:46:08 首次发布

本文链接：https://blog.youkuaiyun.com/m0_67198282/article/details/125447264

版权

Java学习笔记专栏收录该内容

9 篇文章

订阅专栏

本文详细介绍了汉诺塔问题，从基础概念到递归思路解析，再到具体的Java代码实现。通过逐步分析1至n个圆盘的移动策略，揭示了递归解决复杂问题的方法，并提供了模拟移动和递归实现的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2022.6.24

1.什么是汉诺塔？

2.如何去思考汉诺塔

目的：把圆盘从一个柱子挪到另一个柱子

要求：

1.一次只能挪动一个圆盘

2.大圆盘不能放在小圆盘上面

我们现在来结合目的与要求来思考一下如何挪动（由A->C）

（1）假设只有1个圆盘

我们只需要A-->C即可

（2）假设有2个圆盘

我们会发现不能直接从A挪到C了，我们需要借助B来挪动

A->B

A->C

B->C

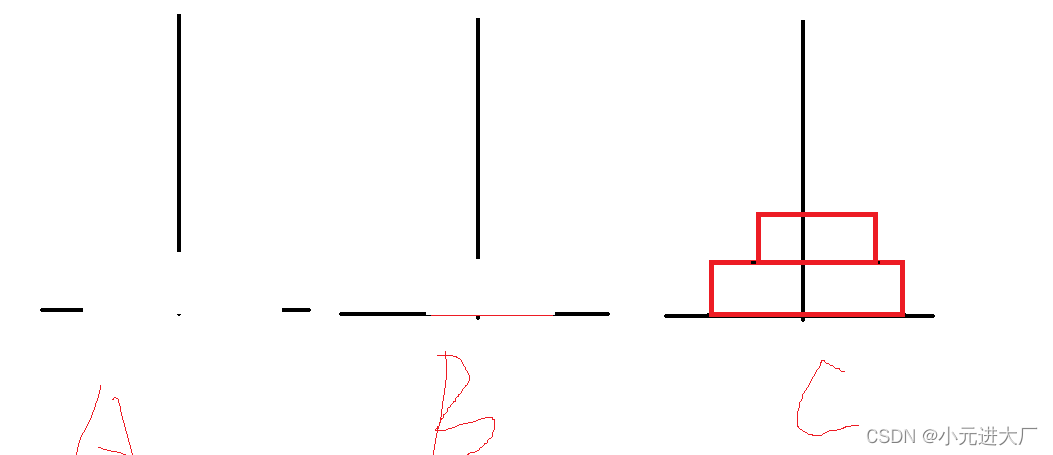
至此，我们就实现了挪动

（3）假设有3个圆盘

A->C A->B

C->B A->C

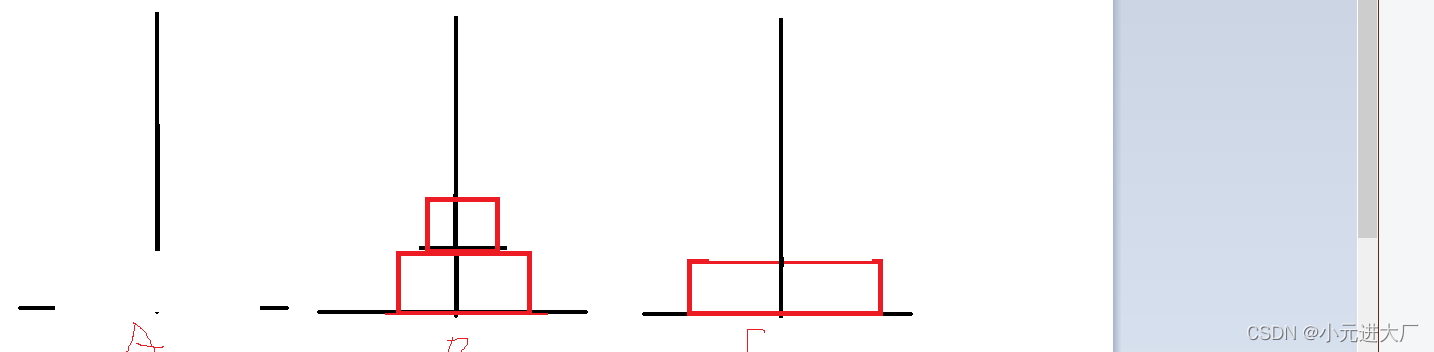
B->A

B->C A->C结束

（4）假设有n个圆盘

我们在上面几个例子中可以发现，无论是几个圆盘，我们都需要先将最后一个圆盘上面的挪到B上，然后在将最后一个圆盘挪到C上

也就是说：我们如果要挪动n个圆盘，就需要先将上面的n-1个圆盘经过C来挪到B上，然后再把第n个圆盘挪到C上。然后我们需要将在B上的n-2个圆盘经过C挪到A上，然后把第n-1个圆盘挪到C上.....以此类推

以下为图解

我们把第n个圆盘挪到C之后，只需要把n-1个圆盘也挪到C就可以完成了。

那么我们如何把剩下的n-1个挪到C上呢？

我们可以参考上面的方法来挪动

以此类推

3.代码实现

（1）模拟移动

pos1为起始位置，pos2为挪动后的位置

（2）递归汉诺塔

我们了解思想之后，写出完整代码

public class hannoi {
    public static void move (char pos1, char pos2) {
        System.out.println(pos1+"->"+pos2);
    }

    /**
     * 汉诺塔
     * @param n  圆盘的个数
     * @param pos1  起始位置
     * @param pos2  中途经过的位置
     * @param pos3  最终要到达的位置
     */
    public static void hanNoi(int n, char pos1, char pos2, char pos3) {
        if(n==1){
            move(pos1,pos3);//只有一个盘子，直接从A挪到C
        }else{
            hanNoi(n-1,pos1,pos3,pos2);//先把n-1个盘子从A经过C挪到B
            move(pos1,pos3);//把第n个盘子从A挪到C
            hanNoi(n-1,pos2,pos1,pos3);//把剩下的n-1个盘子从B经过A挪到C
        }
    }
    public static void main(String[] args) {
        hanNoi(3,'A','B','C');
    }
}