【MATLAB】自控建模第一节--传输函数与零极点图

1. 连续系统的时域响应

        连续时间LTI系统可用如下的线性常系数微分方程来描述：

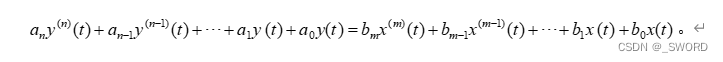
        已知输入信号x(t)以及系统初始状态，就可以求出系统的响应。MATLAB提供了微分方程的数值计算的函数，可以计算上述n阶微分方程描述的连续系统的响应，包括系统的单位冲激响应、单位阶跃响应、零输入响应、零状态响应和完全响应。

        在调用MATLAB函数时，需要利用连续系统对应的系数函数。对微分方程进行Laplace变换即可得系统函数：

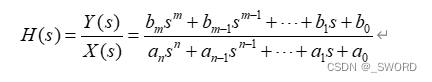
在MATLAB中可使用向量和向量分别保存分母多项式和分子多项式的系数：

   

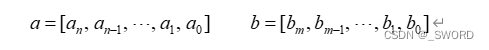
这些系数均按s的降幂直至s0排列。

(1) 连续系统的单位冲激响应h(t)的计算

impulse(sys)计算并画出系统的冲激响应。参数：sys可由函数tf(b,a)获得。其中： 

h=impulse(sys, t): 计算并画出系统在向量t定义的区间上的冲激响应，向量h保存对应区间的系统冲激响应的输出值。

(2) 连续系统的单位阶跃响应h(t)的计算

step(sys): 计算并画出系统的阶跃响应。

g=step(sys, t): 计算并画出系统在向量t定义的区间上的阶跃响应，向量g保存对应区间的系