旋转矩阵转欧拉角，转四元数

我们在进行三维重建的过程之中，进行标定的时候，尤其是两个或者多个相机而言，需要知道相对位置姿态，但是相互转化的过程中会遇到使用旋转矩阵求解问题。一般是很难在三维旋转矩阵之中找到我们想要知道的量，因此，这里是将旋转矩阵进行转换的过程，以及各个过程之中需要注意的地方。

旋转矩阵转旋转向量的过程，在下载资源之中，之前已经整理过了，这里就不再进行整理，请看博客的下载资源。

• 欧拉角

1.二维空间旋转矩阵的情况：

 上述的点坐标可以进行一个如下表示：（优快云中的公式编辑器是真的难用）

 可以得到如下关系：

 2.三维空间旋转矩阵的情况：右手坐标系下

旋转表示如下所示：

 上述之中的y方向是在右手坐标系下，因此，sin和cos的情况是和x、y方向是不同的。

3.万向节死锁问题的出现

这个理解过程直接是使用公式进行理解

这里当关于y轴旋转90度的时候，就是会可以将它看成只是按照x轴进行旋转，这就是产生万向节死锁的原因。

• 轴角表示

 又因为叉乘遵守分配律，所以

 进而得知，

 其实这就是一个罗德里格斯公式的推导过程，具体的使用过程是见博客之中罗格里格斯公式的推导，具体中有矩阵的使用。

• 四元数形式

1.复数之中的运算用矩阵表示如下所示：

 可见矩阵是满足交换律的，这里应当注意的是如何使用复数表示矩阵。

特殊的矩阵表达形式

2. 复数与二维旋转

 其前面的矩阵称为缩放矩阵，后面的是旋转矩阵。

 3.两种转换形式

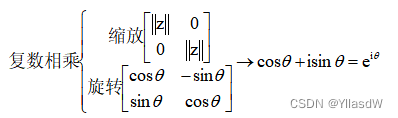
 4.四元数与角轴之间的转换

 详见博客文档下载，我写到一个word里面了，可以下载看看，博客可真是个存档的好东西。​​​​​​​​​​​​​​https://download.youkuaiyun.com/download/m0_47489229/86609016https://download.youkuaiyun.com/download/m0_47489229/86609016