跟李沐学AI part3

SCUT-Chung

已于 2022-04-07 23:39:26 修改

阅读量504

点赞数 1

分类专栏： ML 文章标签： python pytorch 神经网络

于 2021-10-05 13:36:19 首次发布

本文链接：https://blog.youkuaiyun.com/m0_46861439/article/details/120609435

版权

ML 专栏收录该内容

12 篇文章

订阅专栏

0.总体速率

完成入门训练时（比如cifa10和mnist的时候可以来参考）
在这里插入图片描述

1.层与块

层：一种函数
块：多层组合在一起。

class MLP(nn.Module):
    # 用模型参数声明层。这里，我们声明两个全连接的层
    def __init__(self):
        # 调用`MLP`的父类`Block`的构造函数来执行必要的初始化。
        # 这样，在类实例化时也可以指定其他函数参数，例如模型参数`params`（稍后将介绍）
        super().__init__()
        self.hidden = nn.Linear(20, 256)  # 隐藏层
        self.out = nn.Linear(256, 10)  # 输出层

    # 定义模型的正向传播，即如何根据输入`X`返回所需的模型输出
    def forward(self, X):
        # 注意，这里我们使用ReLU的函数版本，其在nn.functional模块中定义。
        return self.out(F.relu(self.hidden(X)))

比如上面的hidden和out就分别是一层
而将几个层组合在一起称之为块

在这里记录一个有点反直觉的写法

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for block in args:
            # 这里，`block`是`Module`子类的一个实例。我们把它保存在'Module'类的成员变量
            # `_modules` 中`block`的类型是OrderedDict，意味着它是有序的
            #不用列表是因为列表中的元素是无序的，使用的话会造成网络成员错搭，造成128*256*784*256这种会报错的情况
            #这个_modules是一个字典
            self._modules[block] = block

    def forward(self, X):
        # OrderedDict保证了按照成员添加的顺序遍历它们
        for block in self._modules.values():
        #表示网络对网络的迭代比如 linear1（linear0）
        #或者你也可以认为是嵌套，就是以上一层的输出作为下一层的输入
            X = block(X)
        return X

2. 参数

2.1 访问参数

#n表示第n层
net[n].state_dict()  #提供weight与bias
net[n].bias  #打印bias
net[n].bias.data #访问数据并可以修改
net[n].bias.grad #访问梯度
net.named_parameters()  #一次访问所有的参数
net.state_dict()['位置.参数'].data #参数=biad/weight,效果类似于net[n].bias.data
#需要注意的是在计算层数的时候它也会把relu算进去，但不打印它的参数（也打印不了上面东西）

print(net)  #用于展示整个网络结构

在这里插入图片描述

2.1.2 修改默认参数

def init_normal(m):
    if type(m) == nn.Linear:
    #_ 表示替换
        nn.init.normal_(m.weight, mean=0, std=0.01)  #这里指定替换 m.weight
        nn.init.zeros_(m.bias) #这里指定替换 m.bias

net.apply(init_normal)  #这里指对多有的层的参数做上述的替换
net[0].apply(init_normal) #这里指对第一层的参数做替换
net[0].weight.data[0], net[0].bias.data[0]

#也有下面的暴力写法
net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42
net[0].weight.data[0]

需要注意的是不能将权重初始化为常数，应为这样对于梯度更新而言，每次的更新量都是相同的，传到最初的函数里头，更新量也是相同的，那么 w_new=w-lr*(dw/dx)的时候，得到的结果也是行相同的，按照行列式的计算来说（两行相同结果为0）就没有达到跟新的效果。可能还是i有点不清楚，就是每个w里的元素在更新后的它们还是相同的，，这就会形成一种限制，使他永远都达不到目标效果（比如目标效果是【【1，2】，【3，4】】，但因为限制可能达到的是【【1.5，1.5】，【1.5，1.5】】）

2.1.3 共享权重 / 参数绑定

更新的时候相同的标记处的值是相同的

shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.Linear(8, 1))

2.2 自定义层

这里主要是想讲一下这个 nn.Parameter()的用法
1.nn.Parameter(balabala)：将一个固定不可训练的tensor转换成可以训练的类型parameter，并将这个parameter绑定到这个module里面，所以经过类型转换这个self.v变成了模型的一部分，可以在模型训练中更新

2.nn.Parameter()：直接调用的话会返回这个模型的参数

下面是使用nn.Parameter()来定义一层

class MyLinear(nn.Module):
    def __init__(self, in_units, units):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(in_units, units))
        self.bias = nn.Parameter(torch.randn(units,))
    def forward(self, X):
        linear = torch.matmul(X, self.weight.data) + self.bias.data
        return F.relu(linear)

3.储存与加载

3.1 向量的储存与加载

单个的话可以直接调用save

x = torch.arange(4)
torch.save(x, 'x-file')

多个的话通过字典就可以实现

mydict = {'x': x, 'y': y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')

3.2 模型的储存

不仅要加载参数，也要加载模型的定义
加载模型的定义后会将里面的参数初始化，这时再加载参数就能达到模型的复原
eg.

class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(20, 256)
        self.output = nn.Linear(256, 10)

    def forward(self, x):
        return self.output(F.relu(self.hidden(x)))

net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)

#储存
torch.save(net.state_dict(), 'mlp.params')

#模型恢复
clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()

4.卷积

4.0

https://www.bilibili.com/video/BV1L64y1m7Nh?p=1
在这里插入图片描述
MLP的缺点：
100个mlp以100个全连接层为输出
y=w*（x.T）+b
36k–>flatten->136k
意味着每一个神经元（i）都要有36k个对应的wij，j<=36k
w=10036k（矩阵）
所以共有36k*100=3.6b个元素

4.1卷积的由来

没咋听懂，他日再写

4.2 卷积的直观感觉

在这里插入图片描述

4.3代码

在这里插入图片描述

那个backward会把求出来的梯度丢到了conv2d.

4.4 步幅

就是卷积核计算的时候，每次沿长、宽移动相应距离后再进行运算

4.5.1多通道输入

卷积核的第四个维度的数值是1
卷积的结果是每一层与对应层的卷积核运算后的数值之和
在这里插入图片描述

4.5.2 多通道输出

与多通道输入的差别在于第四维度，就是表示有多少个三维核的维度的数值不只是1
这里的i表示第几个通道，想法是有多个三维的卷积核来对应多个输出
在这里插入图片描述
多通道输出

可以认为每一个输出通道是在寻找一种模式

5.池化层（pooling）

这是用来克制卷积的敏感性（大方向的分类的敏感性不要这么高），在发现一个特征之后，它的精确位置远不及它和其他特征的相对位置的关系重要。
就比如说识别一个橘猫，不应该因为橘猫的毛有一片白毛就把他从橘猫里面排除。
有两种池化层：max pooling 和avrerage pooling

如果说卷积层的运算分两步：摆位置，对应计算
那么pooling运算的第一步和卷积是相同的，第二步对应计算则是求max或平均值
在这里插入图片描述

5.1 填充和步幅（卷积和池化都用这个算，池化的话视padding=0）

在这里插入图片描述

5.2 多输入与多输出

它是对每一个通道都执行一种操作，没有拼接也没有像卷积输出通道树由卷积核的数量决定（应该说是第四维度的数值）
输入通道数=输出通道数

6. LeNet

卷积-激活-池化记得这个三件套
卷积将通道数变多认为是将特征提取出来，并放在通道中
通道数可以认为是模式（就是判断某一特征的），mlp（感知机）的思想就是将这些模式组合起来（加法），加以权重最后构造出一个完整的模型
说实话，就是按着他的论文的图用sequetial连接起来
在这里插入图片描述

import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt


class Reshape(torch.nn.Module):
    def forward(self, x):
        return x.view(-1, 1, 28, 28)

net = torch.nn.Sequential(
    Reshape(),
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)


batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    for X, y in data_iter:
        if isinstance(X, list):
            # BERT微调所需的（之后将介绍）
            X = [x.to(device) for x in X]
        else:
            X = X.to(device)
        y = y.to(device)
        metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]






#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)。"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()

    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，范例数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]

        test_acc = evaluate_accuracy_gpu(net, test_iter)
        loss_l.append(train_l)
        train_a_l.append(train_acc)
        test_a_l.append(test_acc)
        #这里这样写是因为由于pytorch的问题他会显示一片红色的userwarning，观感不友好，所以最后在列表那边展示出来
        #print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
         #     f'test acc {test_acc:.3f}')
        #print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
        #      f'on {str(device)}')


lr, num_epochs = 0.5, 60

if __name__ == '__main__':
    loss_l = []
    train_a_l = []
    test_a_l = []
    epoch_l=[]
    train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
    for i in range(int(len(loss_l))):
        epoch_l.append(i+1)
        print(f'loss {loss_l[i]:.3f}, train acc {train_a_l[i]:.3f}, '
             f'test acc {test_a_l[i]:.3f}')

    plt.subplot(111)
    # 加网线格子
    plt.grid(linestyle=':')
    plt.xlabel(r'$epoch$', fontsize=14)
    plt.plot(epoch_l, train_a_l, c='dodgerblue', label=r'$train acc$')
    plt.plot(epoch_l, test_a_l, c='orangered', label=r'$test acc$')
    plt.legend()
    plt.subplot(111)
    plt.figure('loss', facecolor='lightgray')
    plt.title('loss', fontsize=20)
    plt.xlabel(r'$epoch$', fontsize=14)
    plt.ylabel(r'$loss$', fontsize=14)
    plt.plot(epoch_l, loss_l, c='limegreen', label=r'$loss$')
    plt.show()

有点过拟合了，但我懒得调了
在这里插入图片描述

7.AlexNet

在这里插入图片描述

写下计算：

在这里插入图片描述

果然后买你加了一层linear（256* 5* 5，4096）

然后按照上面的参数，主要是第三个维度（深度）来制定
有些许改动，主要是那个动画类再pycharm上表现不了

import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt

net=nn.Sequential(
    nn.Conv2d(1,96,kernel_size=11,stride=4,padding=1),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2),
    nn.Conv2d(96,256,kernel_size=5,padding=2),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2),
    nn.Conv2d(256,384,kernel_size=3,padding=1),
    nn.ReLU(),
    nn.Conv2d(384, 384,kernel_size=3, padding=1),
    nn.ReLU(),
    nn.Conv2d(384, 256,kernel_size=3, padding=1),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2),
    #要准备进入全连接层了，所以flatten
    nn.Flatten(),
    nn.Linear(256*5*5,4096),
    nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096),
    nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 10))


def evaluate_accuracy_gpu(net, data_iter, device=None): 
    if isinstance(net, torch.nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    for X, y in data_iter:
        if isinstance(X, list):
            # BERT微调所需的（之后将介绍）
            X = [x.to(device) for x in X]
        else:
            X = X.to(device)
        y = y.to(device)
        metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]


def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)。"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()

    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，范例数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]

        test_acc = evaluate_accuracy_gpu(net, test_iter)
        loss_l.append(train_l)
        train_a_l.append(train_acc)
        test_a_l.append(test_acc)
        print(f'epoch{epoch+1},loss {train_l:.3f}, train acc {train_acc:.3f}, '
              f'test acc {test_acc:.3f}')



if __name__ == '__main__':
    batch_size = 32
    train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
    lr = 0.01
    num_epochs = 30





    loss_l = []
    train_a_l = []
    test_a_l = []
    epoch_l=[]
    train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
    for i in range(int(len(loss_l))):
        epoch_l.append(i+1)
        print(f'loss {loss_l[i]:.3f}, train acc {train_a_l[i]:.3f}, '
             f'test acc {test_a_l[i]:.3f}')

    plt.subplot(111)
    # 加网线格子
    plt.grid(linestyle=':')
    plt.xlabel(r'$epoch$', fontsize=14)
    plt.plot(epoch_l, train_a_l, c='dodgerblue', label=r'$train acc$')
    plt.plot(epoch_l, test_a_l, c='orangered', label=r'$test acc$')
    plt.legend()
    plt.subplot(111)
    plt.figure('loss', facecolor='lightgray')
    plt.title('loss', fontsize=20)
    plt.xlabel(r'$epoch$', fontsize=14)
    plt.ylabel(r'$loss$', fontsize=14)
    plt.plot(epoch_l, loss_l, c='limegreen', label=r'$loss$')
    plt.show(）

效果：
在这里插入图片描述

8.VGG

旧时代研究员们发现同样的计算开销下33的卷积核的效果更好
想法是将 3 3的卷积核堆叠再一起形成一个块（不清楚多少个），并再接下来模型的定义中用块来实现
它和AlexNet的区别就是VGG把后面连续的卷积核组合在了一起并代替AlexNet中的较大卷积核（11x11，7x7，5x5），再删去了前面的相对不怎么规则的卷积-pooling结构
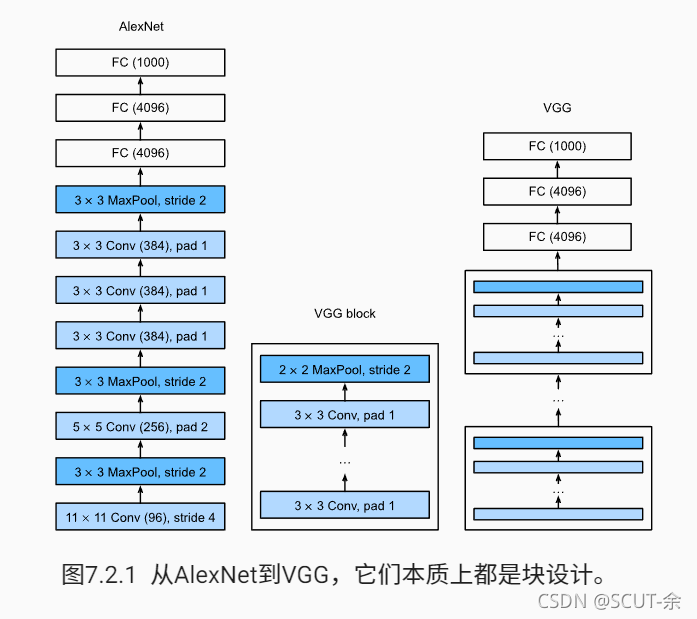
在这里插入图片描述

在这里插入图片描述

#特色一：块的设计
#反正用的都是 3*3的卷积和，所以只需要input_num和output_num就行了
#除了第一个要变化下维度，输入=in_channel,输出=out_channels,其他的卷积层的输入和输出都等于out_channels
#最后再maxpooling,kernel_size=2,stride=2
def vgg_block(num_conv,in_channels,out_channels):
    layers=[]
    for i in range(num_conv):
        layers.append(nn.Conv2d(in_channels,out_channels
                                ,kernel_size=3,padding=1))
        layers.append(nn.ReLU())
        in_channels=out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

#vgg19
conv_arch=((2,64),(2,128),(4,256),(4,512),(4,512))
#来说一下数据的变换，再块里面数据的尺寸是不变的，在块之间有变换罢了
#都是指经过这一层处理后的输出
#in---1*1*224*224
#（2，64）---1*64*112*112。（conv）224-3+1*2=+1=224，（maxpooling） （224-2）/2+1=112相当于直接除以2
#（2，128）---1*128*56*56，112/2=56
#（4，256）---1*256*28*28，56/2=28
#（4，512）---1*512*18*18，28/2=14
#（4，512）---1*512*7*7，14/2=7

#nn.Sequential的功能强大，甚至可以直接把块连接起来
def vgg(conv_arch):
    conv_blks=[]
    in_channels=1

    for (num_convs,out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs,in_channels,out_channels))
        in_channels=out_channels

    return nn.Sequential(
        *conv_blks,
        nn.Flatten(),
        nn.Linear(out_channels*7*7,4096),nn.ReLU(),nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096,10)
    )

9.额外说一下网络的组合

1.conv: 一般后接relu再接conv（VGG块以及AlexNet），或者接maxpooling
2.一般linear后接relu，再接dropout

-> CONV/FC -> BatchNorm -> ReLu(or other activation) -> Dropout -> CONV/FC ->；
在这里插入图片描述

在这里插入图片描述

10 GoogLeNet

第一个到100层的卷积
问题是再考虑不同kernel_size的卷积层哪个的效果好点
想法是：我全都要！所以定义了inception块，4条线得到的结果合并在一起（不是拼接），通道数等于四条线输出的通道数之和而输入输出的长宽相同（即incep块不改变通道数）

合并的样子
在这里插入图片描述

在这里插入图片描述

紫色表示每条线通道数的规划

在这里插入图片描述

特色：创建inception

class Inception(nn.Module):
    # `c1`--`c4` 是每条路径分配的输出通道数
    def __init__(self,in_channels,c1,c2,c3,c4,**kwargs):
        super(Inception,self).__init__(**kwargs)
        # 线路1，单1 x 1卷积层
        self.p_1=nn.Conv2d(in_channels,c1,kernel_size=1)
        # 线路2，1 x 1卷积层后接3 x 3卷积层
        self.p_2_1=nn.Conv2d(in_channels,c2[0],kernel_size=1)
        self.p_2_2=nn.Conv2d(c2[0],c2[1],kernel_size=3,padding=1)
        # 线路3，1 x 1卷积层后接5 x 5卷积层
        self.p_3_1=nn.Conv2d(in_channels,c3[0],kernel_size=1)
        self.p_3_2=nn.Conv2d(c3[0],c3[1],kernel_size=5,padding=2)
        # 线路4，3 x 3最大汇聚层后接1 x 1卷积层
        self.p_4_1=nn.MaxPool2d(kernel_size=3,padding=1,stride=1)
        self.p_4_2=nn.Conv2d(in_channels,c4,kernel_size=1)

    def forward(self,x):
    #F.relu可在任意地方使用，可nn.relu只能在容器比如 nn.Sequential中用
        p1=F.relu(self.p_1(x))
        p2=F.relu(self.p_2_2(F.relu(self.p_2_1(x))))
        p3 = F.relu(self.p_3_2(F.relu(self.p_3_1(x))))
        p4= F.relu(self.p_4_2(self.p_4_1(x)))
        # 通道数*深度*长*宽，dim=1表示在深度上拼接
        return torch.cat((p1,p2,p3,p4),dim=1)

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
import matplotlib.pyplot as plt



class Inception(nn.Module):
    # `c1`--`c4` 是每条路径分配的输出通道数
    def __init__(self,in_channels,c1,c2,c3,c4,**kwargs):
        super(Inception,self).__init__(**kwargs)
        # 线路1，单1 x 1卷积层
        self.p_1=nn.Conv2d(in_channels,c1,kernel_size=1)
        # 线路2，1 x 1卷积层后接3 x 3卷积层
        self.p_2_1=nn.Conv2d(in_channels,c2[0],kernel_size=1)
        self.p_2_2=nn.Conv2d(c2[0],c2[1],kernel_size=3,padding=1)
        # 线路3，1 x 1卷积层后接5 x 5卷积层
        self.p_3_1=nn.Conv2d(in_channels,c3[0],kernel_size=1)
        self.p_3_2=nn.Conv2d(c3[0],c3[1],kernel_size=5,padding=2)
        # 线路4，3 x 3最大汇聚层后接1 x 1卷积层
        self.p_4_1=nn.MaxPool2d(kernel_size=3,padding=1,stride=1)
        self.p_4_2=nn.Conv2d(in_channels,c4,kernel_size=1)

    def forward(self,x):
        p1=F.relu(self.p_1(x))
        p2=F.relu(self.p_2_2(F.relu(self.p_2_1(x))))
        p3 = F.relu(self.p_3_2(F.relu(self.p_3_1(x))))
        p4= F.relu(self.p_4_2(self.p_4_1(x)))
        # 通道数*深度*长*宽，dim=1表示在深度上拼接
        return torch.cat((p1,p2,p3,p4),dim=1)

b1=nn.Sequential(nn.Conv2d(1,64,kernel_size=7,stride=2,padding=3),
                 nn.ReLU(),
                 nn.MaxPool2d(kernel_size=3,stride=2,padding=1),
                 nn.Conv2d(64,64,kernel_size=1,padding=1,stride=1),
                 nn.ReLU(),
                 nn.Conv2d(64,192,kernel_size=3,padding=1,stride=1),
                 nn.ReLU(),
                 #原文没有这个relu
                 nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
                 )

b3=nn.Sequential(Inception(192,64,(96,128),(16,32),32),
                 Inception(256,128,(128,192),(32,96),64),
                 nn.MaxPool2d(kernel_size=3,stride=2,padding=1),
                 )

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())
net = nn.Sequential(b1, b3, b4, b5, nn.Linear(1024, 10))




def evaluate_accuracy_gpu(net, data_iter, device=None):
    """使用GPU计算模型在数据集上的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    for X, y in data_iter:
        if isinstance(X, list):
            # BERT微调所需的（之后将介绍）
            X = [x.to(device) for x in X]
        else:
            X = X.to(device)
        y = y.to(device)
        metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]







def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)。"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()

    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，范例数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]

        test_acc = evaluate_accuracy_gpu(net, test_iter)
        loss_l.append(train_l)
        train_a_l.append(train_acc)
        test_a_l.append(test_acc)
        print(f'epoch{epoch+1},loss {train_l:.3f}, train acc {train_acc:.3f}, '
              f'test acc {test_acc:.3f}')
        #print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
        #      f'on {str(device)}')




if __name__ == '__main__':
    loss_l = []
    train_a_l = []
    test_a_l = []
    epoch_l=[]
    #conv_arch=((2,64),(2,128),(4,256),(4,512),(4,512))
    net = nn.Sequential(b1, b3, b4, b5, nn.Linear(1024, 10))





    lr, num_epochs, batch_size = 0.1, 10, 64




    train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
    train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

#集体打印，避免奇怪的userwarning毁掉观感
    for i in range(int(len(loss_l))):
        epoch_l.append(i+1)
        print(f'loss {loss_l[i]:.3f}, train acc {train_a_l[i]:.3f}, '
             f'test acc {test_a_l[i]:.3f}')


#作图
    plt.subplot(111)
    # 加网线格子
    plt.grid(linestyle=':')
    plt.xlabel(r'$epoch$', fontsize=14)
    plt.plot(epoch_l, train_a_l, c='dodgerblue', label=r'$train acc$')
    plt.plot(epoch_l, test_a_l, c='orangered', label=r'$test acc$')
    plt.legend()
    plt.subplot(111)
    plt.figure('loss', facecolor='lightgray')
    plt.title('loss', fontsize=20)
    plt.xlabel(r'$epoch$', fontsize=14)
    plt.ylabel(r'$loss$', fontsize=14)
    plt.plot(epoch_l, loss_l, c='limegreen', label=r'$loss$')
    plt.show()

在这里插入图片描述

11.批量归一化（能加快收敛但对准确率提升没什么影响）

11.1 问题提出与方案

问题：在做backward的时候，钱买你的梯度较大，后面的由于是多个小于1的数相乘，它们的梯度特别小，这导致对靠近数据这端的层权重更新非常缓慢而无力。而每次底端（靠近数据的那端）一遍，上面就要根据这些重新学习很多次，导致整个模型收敛变慢，消耗很多时间。

现在的想法就是能不能高出一个方案，使得底部变的时候顶部（靠近输出端）不变

解决方法：批量归一化。
为什么会改变频繁？从数学的稳定性来说，因为方差和均值在不同层之间是不同的，如果把它们的分布固定了，稳定性就高了，优化所能改动的只剩下细微的部分

11.2直观

在这里插入图片描述

11.3 每一行是一个样本，每一列是一个特征

解释（我的理解）：
样本是由特征构成的，比如一个样本a1可以由x1,x2,…xn这些特征构成，那么对应于一个全连接层来说，它就是要找到n个权重来构成这个判别的模型，并且最后提供一个判别的分数，那就是1n（样本）n 1(权重矩阵)=1 1，
最后有m个样本，要得到m个判别值，就是m* n* n* 1=m1
将mn展开来看，即是每一行是一个样本，每一列是一个特征

11.3.5 卷积核的个数就是提取的特征

在这里插入图片描述

（2022.4.7修改）上课的时候听老师讲了一下，我们来一个简单点的说法，其实四个维度out_channelin_channelh * h中，out_channel的大小才是你希望从这里提出出来的特征数量，in_channel不过是用来贴合输入的数量，因为这时候我们是做一个复杂的特征提取，就像上面那张图一样，activation的三层和三个卷积核运算才得到一个特征图（一个特征），于是相应的，out_channel是我们希望得到的特征的数量。

效果：lr可以设得大一点，训练时间减少

11.4

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    #eps：防止除数为0，momentum：动量权重
    # 通过 `is_grad_enabled` 来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维（列，dim=1）上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 移动加权平均
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data


class BatchNorm(nn.Module):
    # `num_features`：完全连接层的输出数量或卷积层的输出通道数。
    # `num_dims`：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果 `X` 不在内存上，将 `moving_mean` 和 `moving_var`
        # 复制到 `X` 所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的 `moving_mean` 和 `moving_var`
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y


#位置摆放典例
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
    nn.MaxPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
    nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
    nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
    nn.Linear(84, 10))
    ```