量化的一些paper阅读

z# 前言
这是一项赶鸭子上架的工作，此项工作的目的是把我从一个一无所知的小白变成懂一点神经网络轻量化东西的一年级学生，然后就可以参与大约十天后的文书撰写工作。我也不知道为什么每一年都这么忙。anyway，最重要的是
认知-认同-实践
这份东西主要是我的论文阅读概述，方便我找些东西

1.A White Paper on Neural Network Quantization

https://arxiv.org/pdf/2106.08295.pdf

2.Quantizing deep convolutional networks for efficient inference: A whitepaper

2.0 量化的一些方法

这里只写一些常见的，不常见的情翻原文

2.0.1 Uniform Affine Quantizer（同时也叫非对称量化）

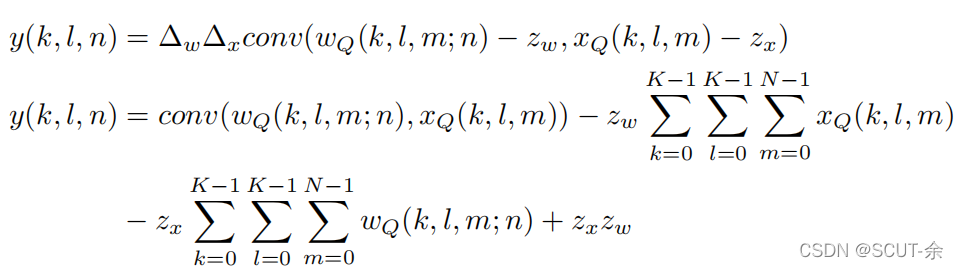
We derive two parameters: Scale (∆) and Zero-point(z) which map the floating point values to integers (See [15]).
Zero-point is an integer, ensuring that zero is quantized with no error. This is important to ensure that common operations like zero padding do not cause quantization error.
这里在说明 zero-point的重要性，个人认为将这个拉过来说明的原因是确切地区分整数0和浮点数0，浮点数0不是在数轴上的确切的0而是一个近零点（float精度误差在1e-6，也就是说只要浮点数的绝对值小于1e-6，就可认为是0），但在round（上面的式子1，如果没有z）中，会采用四舍五入，这样量化出来后的结果就是0，在[2]中是说，“比如padding时，0值也是参与计算的，浮点型的0进行8bit量化后还是0就不对了”，没看懂，mark一下

2.0.2 Uniform symmetric quantizer

和非对称最大的区别就是这里强制zero-point=0，于是一切都变得比较简洁，这里的N_levels=2**（bit），比如int8就对应256

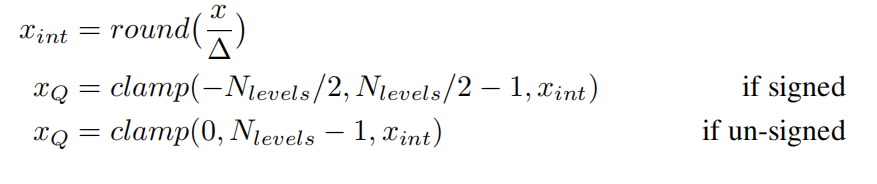
2.1 simulated quantization/ fake quantize

就是这个东西，即先把浮点数值a转为定点，再转为浮点b（我扒帖子后得到的解释是只是训练过程中是浮点参数，保存模型时还是定点保存的）

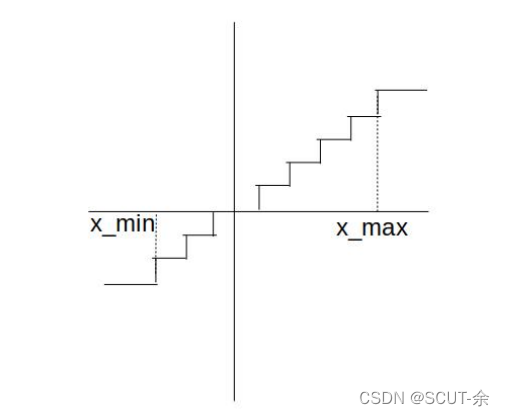
最后的输出结果是上图这个样子的。

来自于【1】

文章接下来提到这么做会导致去量化后得到的是一个导数几乎都是0的函数空间（类似于上面那个阶梯状的图，因为L=f(g…(w))，所以最后得到的导函数是0），前向传播和方向传播的过程参考上面的算法2，里面提了一些重要的点，就是只在前向传播和后向传播中用量化后的权重，该update的时候还是用全精度的。由于几乎为0基本没得update，所以它们用下面的这样的近似来进行更新，

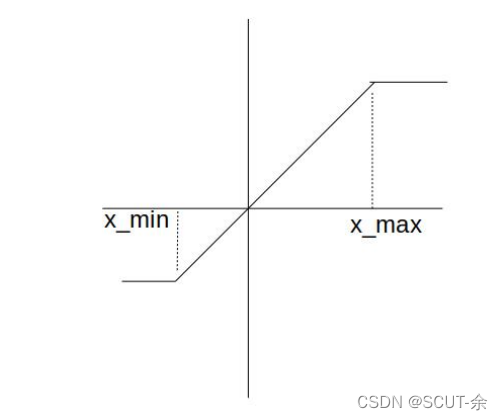
mark一下：因为量化还分训练时量化和训练后量化，我在想驯良后量化不就是直接对权重做一个FP32到int8的变化这种吗，它这里写的应该是训练时量化吧

2.2 方法论

2.2.0 量化的粒度（其实主要讲逐层量化与逐通道量化）

原文在这块写得很粗糙，这里做些补充。
下面是基于[4]来写的，图的话来自于我之前写的[5]。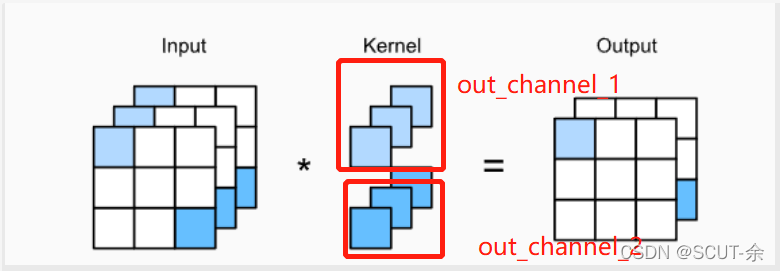

逐层量化与逐通道量化：逐层量化是直接量化一个tensor，比如某一层的weight的形状是：[in_channel, out_channel, h, w]，逐层量化是直接对tensor一步量化(只有一个量化范围和量化步长)。
而逐通道量化是按照out_c维度(参考上图，out_channel的数量自己定的)，逐个通道的进行量化，不同channel的量化range和步长都是各自不同的(总共有out_channel个量化范围和步步长)

2.2.1 确定量化参数

权重：使用实际的最大和最小值来决定量化参数。
激活输出：使用跨批（batches）的最大和最小值的滑动平均值来决定量化参数。
先训练后量化的方法：可以通过仔细地选择量化参数来提高量化模型的精度

2.2.2 Post Training Quantization （训练后量化）

不得不说这种雀氏快，也好操作

2.2.2.1 Weight only quantization

一句话，只将权重的精度从浮点型减低为某个bit（比如int8）整型

2.2.2.1 Quantizing weights and activations

激活值不像权值那样有固定数量，所以这时就得需要标定数据了，即计算激活输出的动态范围，求得量化参数，然后再量化。一般使用100个小批量数据就足够估算出激活输出的动态范围了。

结论：

2.2.3 Quantization Aware Training

训练模拟量化

2.2.3.1

2.reference

[1] https://proceedings.neurips.cc/paper/2015/file/3e15cc11f979ed25912dff5b0669f2cd-Paper.pdf
[2] https://blog.youkuaiyun.com/laozaoxiaowanzi/article/details/107531638?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164923118416780271517780%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=164923118416780271517780&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allfirst_rank_ecpm_v1~rank_v31_ecpm-2-107531638.142^v5pc_search_result_cache,157^v4control&utm_term=Quantizing+deep+convolutional+networks+for+efficient+inference%3A+A+whitepaper+&spm=1018.2226.3001.4187
[3] https://zhuanlan.zhihu.com/p/261059231
[4] https://zhuanlan.zhihu.com/p/352155343
[5] https://editor.youkuaiyun.com/md/?articleId=120609435

3.Searching for Low-Bit Weights in Quantized Neural Networks（2020）

这里是全文的精华所在
记录这个的原因是它与传统的量化的方法有很大的差别
先讲一下这个的idea
假设权重矩阵为W，size=（d1 * d2* … * dn），要进行q bit量化，则*由量化集V={0，1，2，…，2^q -1},
则假定可以通过一个tensor A（m * d1 * d2 * … * dn，其中m=2^q）来描述权重W上某个位置与量化集合V的概率关系，而A（i，…），i∈[1,2,…,m]，描述的是这个位置上的元素属于Vi的概率。
举个例子，假设是4bit量化，n=6，则size(A)=16 * d1 * d2 * d3 * d4 * d5 * d6，则A（11，4，5，6，3，2，1）表示权重W中（4，5，6，3，2，1）的值为V11的概率（V11的数值就是11）
之后经行的softmax不过是做了个归一化，使得概率之和为1
于是用期望来得到Wc，选最大者来得到Wq，之后它会证明随着温度 t 的下降Wq=Wc

4. Binarized Neural Networks

先写点我看不懂的东西，有空再补后续

写的挺奇葩的，也可能是我太菜，在爬了点帖子后，它是这么想的，二值网络对Batch Normalization操作的优化主要是通过AP2(x)操作和<<>>操作来代替普通的乘法。AP2（x）的作用是求与x最接近的2的幂次方，如AP2(3.14)=4,AP2(2.5)=2;而<<>>操作就是位移操作，根据AP2（x）确定<<>>左移右移的位数（因为被搞成了二进制数，而AP2（）出来的都是二的次方，所以可以说时左右移动）。

这里的XnorDotProduct就是普通的同或运算，a0是一个八位的二进制数，每一个bit分别被记为a0^1 ，a0^2…
idea就是把输入先搞成二进制数，然后整个流程就都是二进制数了

。的意思时矩阵对应位置的元素相乘

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Function
import torch.nn as nn
import matplotlib as plt
import d2l

class Binary_a(Function):

    @staticmethod
    def forward(cxt,input):
        cxt.save_for_backward(input)
        output=torch.sign(input)
        return output

    @staticmethod
    def backward(cxt,grad_last):
        input,_=cxt.saved_tensors
        grad_input=grad_last.clone()
        grad_input[input.le(-1)]=0
        grad_input[input.ge(1)]=0
        #按照作者的写法，当sign函数的输入的值大于1的时候，将梯度置0可以得到更好的实验结果
        #至于绝对值小于1的则将其梯度按照1来处理

        return grad_input


# 两个在梯度更新上都是遵照STE的原则-->直接将sign函数跳过，
# 实值weights在更新之后会裁剪到[-1,1]之间，从而减小实值weights和二值化weights之间的距离
# activations的梯度在更新的时候，当实值activations的值大于1时会将梯度置0，避免特别大的梯度向下传递使得训练时候出现震荡

class Binary_w(Function):

    @staticmethod
    def forward(ctx,input):
        output=torch.sign(input)
        return output

    @staticmethod
    def backward(ctx,grad_last):
        grad_input_w=grad_last.clone()
        return grad_input_w


class activation_bin(nn.Module):
    # A=2-->确定是二值化
    def __init__(self,A):
        super().__init__()
        self.A=A
        self.relu=nn.ReLU()

    def binary(self,input):
        output=Binary_a.apply(input)
        return output

    def forward(self,input):
        #确定是二值化
        if A==2:
            output=self.binary(input)
        else:
            output=self.relu(input)
        return output

# 实值weights在更新之后会裁剪到[-1,1]之间，从而减小实值weights和二值化weights之间的距离
def w_clip(w):
    mean=w.data.mean(1,keepdim=True)
    w.data.sub(mean)
    w.data.clamp(-1,1)
    return w

class w_bin(nn.Module):
    #这个w是用来判断是二值化还是三值化的，和上面那个A对称
    def __init__(self,w):
        super(w_bin, self).__init__()
        self.w=w

    def binary(self,input):
        output=Binary_w.apply(input)
        return output

    def forward(self,input):
        #此处input应该是上次更新后的结果
        output_temp=w_clip(input)
        output=self.binary(output_temp)
        return  output

class Conv_bin(nn.Conv2d):
    def __init__(self,in_channels,out_channels,kernel_size,stride=1,padding=0,bias=True,A=2,W=2):
        super().__init__(in_channels=in_channels,out_channels=out_channels,kernel_size=kernel_size,
                       stride=stride,padding=padding,bias=bias)
        self.activation_binary=activation_bin(A)
        self.weight_binary=