【深度学习】感知器、线性神经网络案例应用、BP神经网络算法详细推导

lys_828

于 2022-11-26 08:08:16 发布

阅读量545

点赞数 2

CC 4.0 BY-SA版权

分类专栏：深度学习文章标签：神经网络算法 python bp神经网络推导

本文链接：https://blog.youkuaiyun.com/lys_828/article/details/113387841

深度学习专栏收录该内容

2 篇文章

订阅专栏

本文详细解析了单层感知器的工作原理，包括学习规则和应用案例，进而对比了线性神经网络，并深入探讨了BP神经网络的δ学习规则和梯度下降法。通过实例展示了如何解决异或问题和手写数字识别，揭示了BP算法的推导过程及其向量形式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

手动反爬虫：原博地址

 知识梳理不易，请尊重劳动成果，文章仅发布在优快云网站上，在其他网站看到该博文均属于未经作者授权的恶意爬取信息

如若转载，请标明出处，谢谢！

1. 单层感知器

1.1 感知器的介绍

即模拟人体神经网络，表达的方式有两种，首先介绍第一种
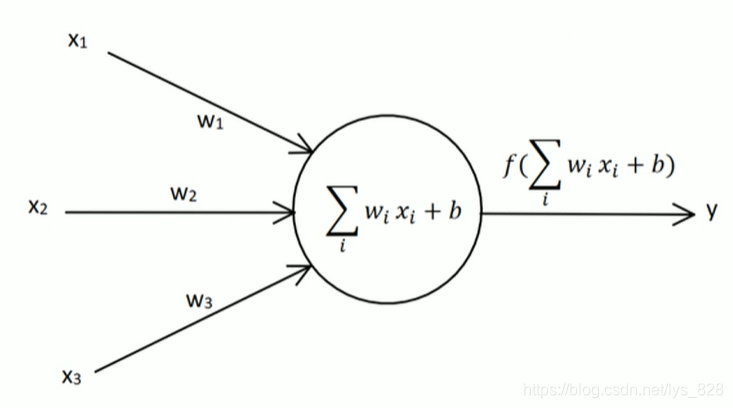
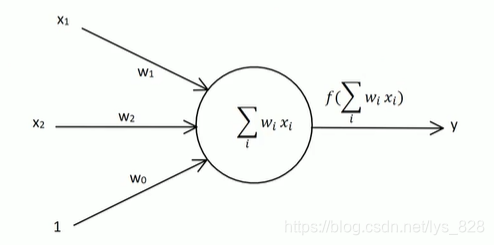
在这里插入图片描述
左侧是输入，右侧是输出，中间的圆形内部进行计算，之后再加上一个激活函数，其中包含的变量的定义，如下：

输入节点： $x_{1},x_{2},x_{3}$
输出节点： $y$
权向量（输入节点对应的权重）： $w_{1},w_{2},w_{3}$
偏置因子： $b$
激活函数： $\left(\begin{matrix} 1, X>=0\\-1,X<0\end{matrix}\right)$ ，这里传入到激活函数中的值是经过圆形内部计算后的值 $X$ ，不是直接输入节点的 $x$ ，因此需要进行强调
目标值（标签）：t（图中没有，但是在权重调整中需要用到）

单层感知器举例（需要特别注意，这里单层感知器的激活函数是信号函数 $s i g n (X)$ ,之后的神经网络是会有不同的激活函数）
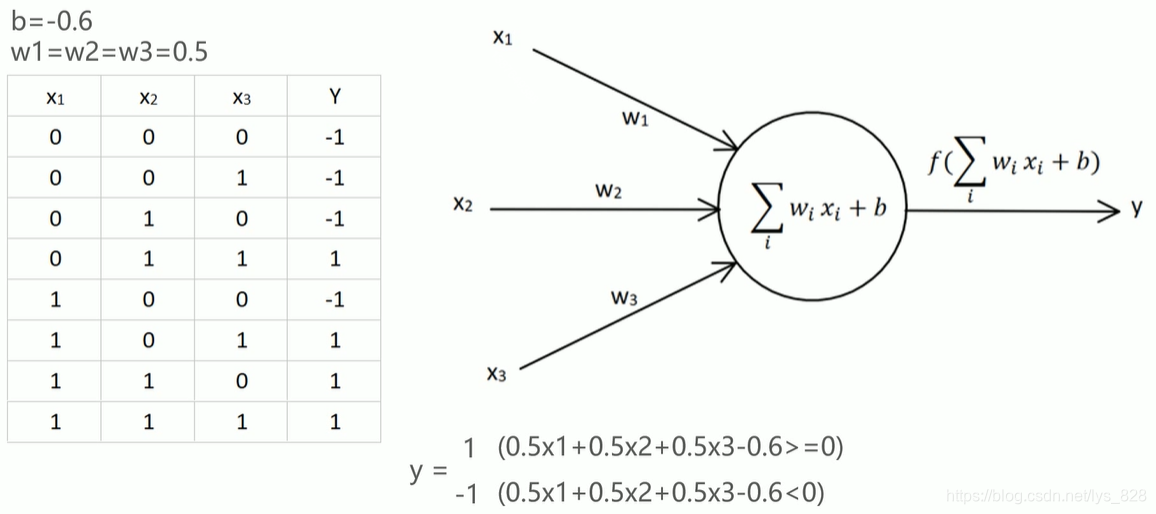
在这里插入图片描述
第二种表示方式，就是将偏置值用 $b = x_{0}*w_{0}$ 形式表示，其中 $x_{0} = 1$ ，也就是将偏置值的符号换了一个表示，即 $\Rightarrow w_{0}$ ，这样公式就可以进行简化了。

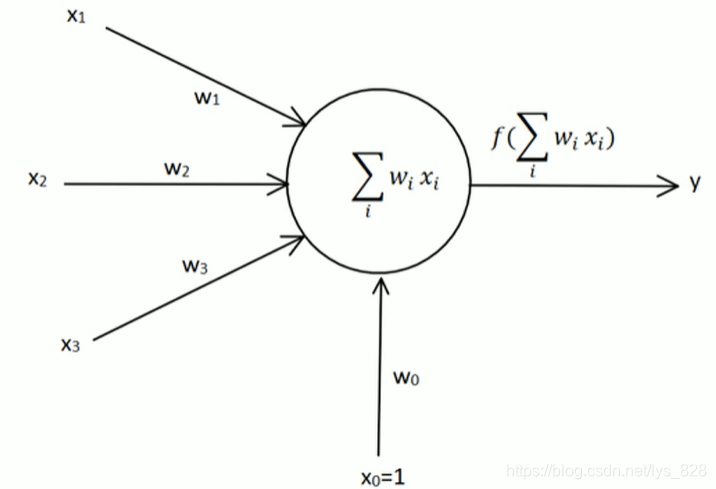
1.2 感知器的学习规则

就是感知器如何进行学习（如何进行自我调整输入节点的权重值），总结概为三步，如下。

第一步：首先计算真实的输出值
第二步：求出各输入节点变化的权重
第三步：更新迭代后的权重

具体的计算图示如下，第二部分注意 $t$ 和 $y$ 的取值
在这里插入图片描述

1.3 感知器单输入输出示例

为了明白感知器是如何自主调整输入权重的过程，同时不进行大量的计算，这里就以一个输入节点进行，对应的图示如下
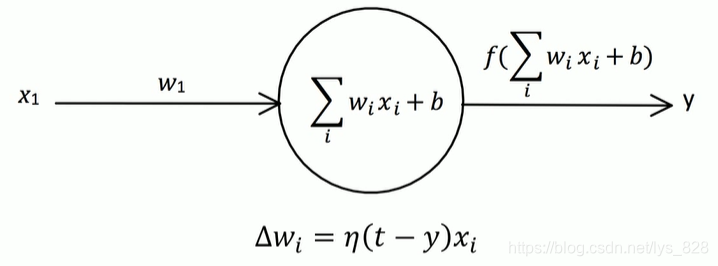
在这里插入图片描述
假定初始值为： $\eta=1,x_{1}=1,w_{1}=-5,b =0$ ，按照上面的步骤进行，第一次计算：
$\Delta w=2*1 = 2, w_{1} = -5+2 = -3$ 第一次计算后得到的实际输出值不位目标值，因此更新权重后继续第二次计算： $\Delta w=2*1 = 2, w_{1} = -3+2 = -1$
还是不一致，接着第三次计算： $\Delta w=2*1 = 2, w_{1} = -1+2 = 1$
第四次计算（目标值与实际输出值一致，停止迭代更新）： $y = s i g n (1 * 1) = 1$

1.4 学习率 $\eta$

这是一个超参数（也就是需要人工手动指定），主要注意三个地方

$\eta$ 取值一般是在0-1之间
学习率太大容易造成权值调整不稳定
学习率太小，权重调整太慢，迭代次数太多

不同学习率对应的模型训练的曲线，只是用来展示，真实情况肯定没有这么平滑
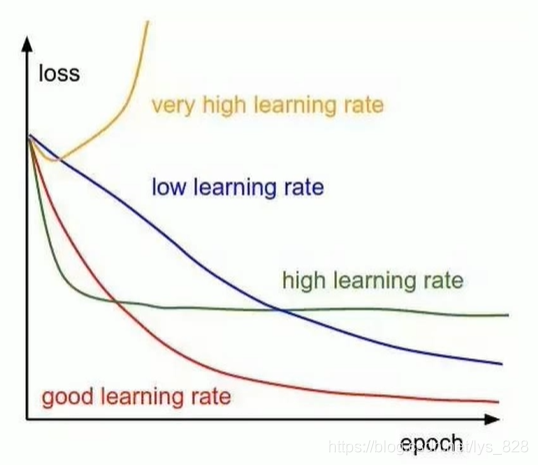
在这里插入图片描述

1.5 模型训练收敛条件

上面示例是计算一个输入节点的感知器模型，最后的输出结果与输出结果一致，但是实际操作过程中往往会是多个节点，而且计算的结果值可能不会等于标签值，因此模型不能无限循环下去，于是就必须制定一个训练收敛的条件，一般是有下面三种情况：

误差小于预先设定的较小的值
两次迭代之间的权值已经很小
设置最大的迭代次数，当迭代次数超过最大次数就停止

2 单层感知器应用案例

2.1 题目

假设我们有4个数据2维的数据，数据的特征分别是(3，3)，(4，3)，(1，1)，(2，1)。(3，3)，(4，3)这两个数据的标签为1，(1，1)，(2，1)这两个数据的标签为-1。构建神经网络来进行分类。

2.2 思路解析

要分类的数据是2维数据，所以只需要2个输入节点，我们可以把神经元的偏置值也设置成一个输入节点。这样我们需要3个输入节点（采用第二种方式进行表达，用程序计算就会很方便）。

2.3 构建模型

（三个输入，一个输出，注意有个是偏置项）
在这里插入图片描述

2.4 数据说明

加入偏置项后，对应的数据

输入数据4个，分别为(1,3,3),(1,4,3),(1,1,1),(1,2,1)
数据标签为(1,1,-1,-1)
初始化的权重可以指定为0-1之间的随机数
学习率假定为0.1
激活函数为sign函数

2.5 代码求解

2.5.1 导入第三方库和构建数据

首先导入科学计算的np库和绘图的plt库，然后按照题目给出的数据进行创建变量，对于Y的设定，这里是为了引入这个变量，给定一个值，方便之后的global声明使用
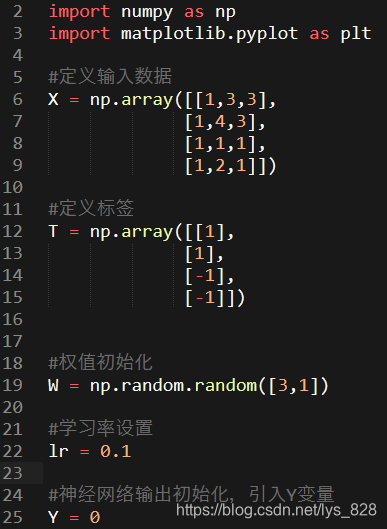
在这里插入图片描述

2.5.2 封装计算过程

通过前面的单输入输出的示例，可以发现中间的计算步骤都是一致的，只是传入的数值不一样，因此可以直接将过程封装成一个函数，多次迭代进行计算就可以了
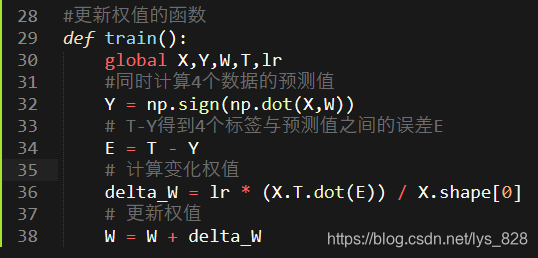
在这里插入图片描述
其中：np.dot(X,W)是用来进行矩阵乘法的计算和下面的X.T.dot(E)一致的效果，后面的也可以使用np.dot(X.T,E)。上面的四行计算的语句就对应着感知器学习的三个步骤，也就完成了权值更新的函数封装

2.5.3 训练模型

前面单步执行权重更新的函数进行循环执行然后判断是否满足条件即可，这里要求程序退出的条件是：计算的输出值要和标签的四个值全部相等，程序才退出，代表模型训练完毕。Y和T都是np.array()对象，直接判断相等，最后返回的还是np.array()对象，故可以直接使用.all()的方法进行元素值的判断
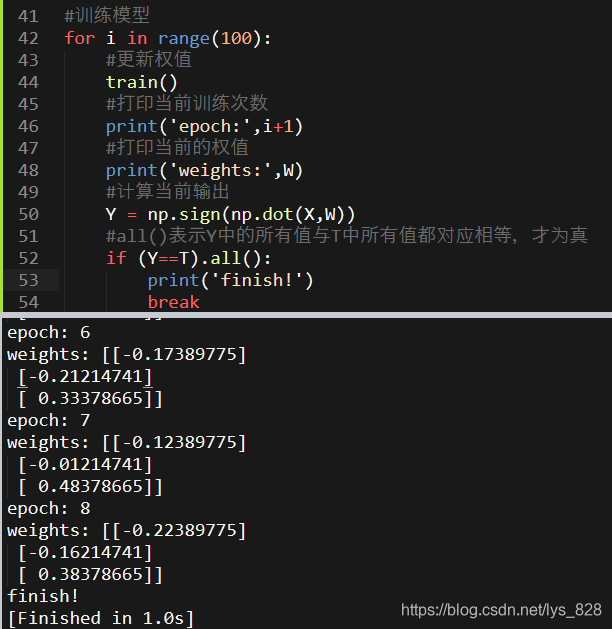
在这里插入图片描述

2.5.4 结果可视化

上面经8个epoch后（也就是8次迭代，由于设置的权重是随机的，所以每次运行的结果可能会不太一样）可以正确的分类，那么具体的结果如何，直接通过上面的代码是没有办法直观的感受到，因此，可以通过绘制图形进行可视化。

补充知识点：关于分类边界线的绘制

直接绘制数据坐标点，很简单，但是绘制分类边界线还需要点数学知识，也就是需要明确得知 直线的斜率和截距。

结合这个具体的案例，采用第二种表示方式进行圆形内部的计算，得到的结果为： $w_{0} + w_{1}*x_{1}+w_{2}*x_{2}$ ，然后通过激活函数求解预测值 $y$ ，圆形内部的计算大于0的时预测值 $y$ 为1，小于0时预测值 $y$ 为-1，因此，圆形内部的计算值等于0就是一个分类的标志，进一步的化简就可以得到 $x_{1}与x_{2}的关系$ ：
$w_{0} + w_{1}*x_{1}+w_{2}*x_{2} = 0 \space \space \space \space \Rightarrow \space \space \space \space x_{2} = -\frac{w_{1}}{w_{2}}x_{1} - \frac{w_{0}}{w_{2}}$

所以直线的斜率和截距也就求解出来了，其中斜率为 $-\frac{w_{1}}{w_{2}}$ ，截距为 $\frac{w_{0}}{w_{2}}$ ，那么接下来就可以绘制图形了
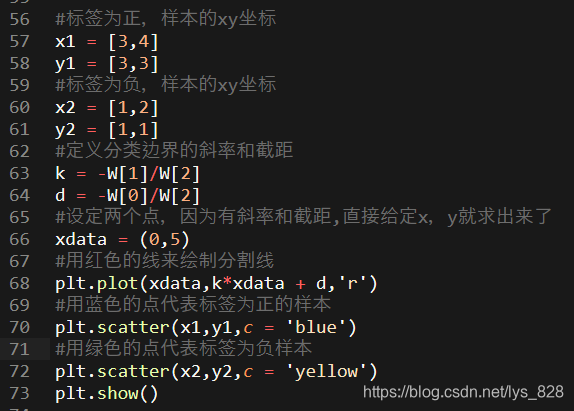
在这里插入图片描述
输出结果为：（由于设置的随机权重，每次运行后产生的结果图形会不一样。进行可视化后，分类结果就很清晰了，至此使用感知器分类的应用案例就分析完毕了）

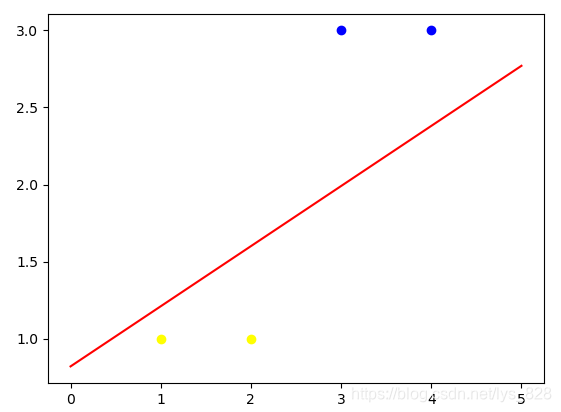
3 线性神经网络

3.1 线性神经网络与单层感知器的对比

线性神经网络在结构上与感知器非常相似，只是激活函数不同。在模型训练是把原来的sign函数换成了pureline函数：y = x

因此就拿上面单层感知器应用案例的代码来看，只需要修改部分就可以。

第一个部分就是激活函数
第二个就是循环执行的判断条件（单层感知器由于输出的是-1和1，也就是分类离散的数据，但是线性神经网络输出的是连续的数据，因此判断条件这里就可以进行删除，只指定迭代的次数就可以了）

import numpy as np
import matplotlib.pyplot as plt

#定义输入数据
X = np.array([[1,3,3],
             [1,4,3],
             [1,1,1],
             [1,2,1]])

#定义标签
T = np.array([[1],
             [1],
             [-1],
             [-1]])


#权值初始化
W = np.random.random([3,1])

#学习率设置
lr = 0.1

#神经网络输出初始化，引入Y变量
Y = 0

#更新权值的函数
def train():
    global X,Y,W,T,lr
    #同时计算4个数据的预测值
    Y = np.dot(X,W)
    # T-Y得到4个标签与预测值之间的误差E
    E = T - Y
    # 计算变化权值
    delta_W = lr * (X.T.dot(E)) / X.shape[0]
    # 更新权值
    W = W + delta_W
    
#训练模型
for i in range(100):
    #更新权值
    train()

#正样本的xy坐标
x1 = [3,4]
y1 = [3,3]
#负样本的xy坐标
x2 = [1,2]
y2 = [1,1]
#定义分类边界的斜率和截距
k = -W[1]/W[2]
d = -W[0]/W[2]
#设定两个点，因为有斜率和截距,直接给定x，y就求出来了
xdata = (0,5)
#用红色的线来绘制分割线
plt.plot(xdata,k*xdata + d,'r')
#用蓝色的点代表正样本
plt.scatter(x1,y1,c = 'blue')
#用绿色的点代表负样本
plt.scatter(x2,y2,c = 'yellow')
plt.show()

输出结果为：（可以看出线性神经网络的分类结果相较于单层感知器来说是较好了，保持了直线在数据的中间位置。单层感知器由于有判断的条件，只要是第一次预测值和标签值相等就停止更新权重了，所以只要分类出来就行了，而线性神经网络是一致迭代直到满足要求的次数即可）
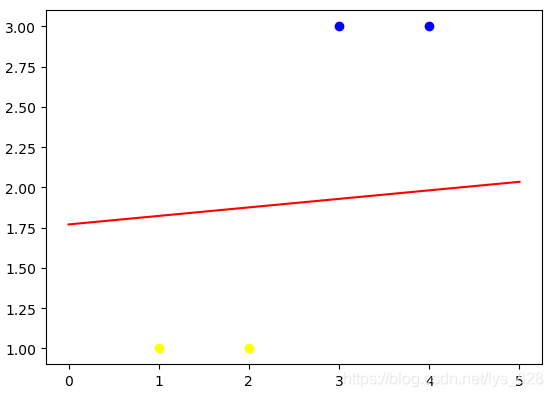
在这里插入图片描述

3.2 线性神经网络-异或问题

异或(数学符号记作‘⊕’)：就是相同为0，不同为1。

a	b	a⊕b
1	1	0
1	0	1
0	1	1
0	0	0

假定有四个数据为(1,1)(1,0),(0,1),(0,0),数据的异或值作为标签，分别为(0),(1),(1),(0)。依然可以使用上面写好的代码，将数据和标签换掉就可以了（这里有个细节的问题，既然是分类的问题，指定标签是1,0可以，指定1，-1也满足，为什么不直接使用1,0，因为在测试输出的时候发现随着迭代的次数越多分类的直线越来越不靠谱，而指定1，-1，最后的结果始终是在四个点所在的区域之间）

# 输入数据
# 4个数据分别对应0与0异或，0与1异或，1与0异或，1与1异或
X = np.array([[1,0,0],
              [1,0,1],
              [1,1,0],  
              [1,1,1]])
# 标签，分别对应4种异或情况的结果
# 注意这里我们使用-1作为负标签
T = np.array([[-1],
              [1],
              [1],
              [-1]])

# 权值初始化，3行1列
# np.random.random可以生成0-1的随机数
W = np.random.random([3,1])

# 学习率设置
lr = 0.1
# 神经网络输出
Y = 0

# 更新一次权值
def train():
    # 使用全局变量X,Y,W,lr
    global X,Y,W,lr
    # 计算网络预测值
    Y = np.dot(X,W)
    # 计算权值的改变
    delta_W = lr * (X.T.dot(T - Y)) / X.shape[0]
    # 更新权值
    W = W + delta_W

# 训练100次
for i in range(100):
    #更新一次权值
    train()

#————————以下为画图部分————————#
# 正样本
x1 = [0,1]
y1 = [1,0]
# 负样本
x2 = [0,1]
y2 = [0,1]

#计算分界线的斜率以及截距
k = - W[1] / W[2]
d = - W[0] / W[2]

# 设定两个点
xdata = (-2,3)
# 通过两个点来确定一条直线，用红色的线来画出分界线
plt.plot(xdata,xdata * k + d,'r')
# 用蓝色的点画出正样本
plt.scatter(x1,y1,c='b')
# 用黄色的点来画出负样本
plt.scatter(x2,y2,c='y')
# 显示图案
plt.show()

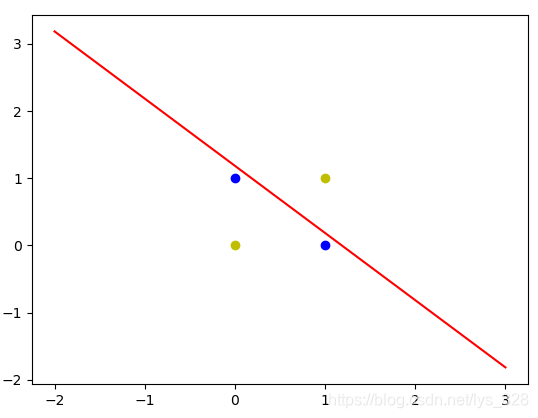
输出结果为：（可以发现线性神经网络无法解决异或的问题）
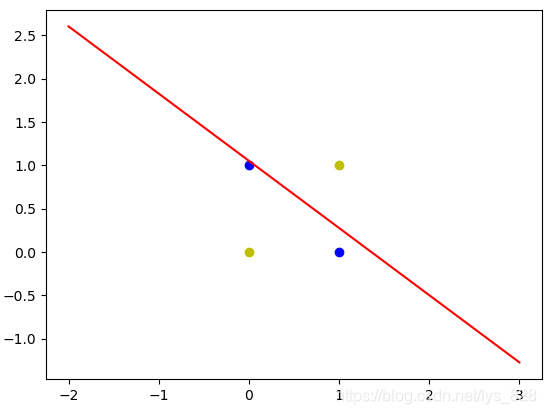
在这里插入图片描述
如果把标签改成1,0，且迭代次数为1000，输出的结果为：

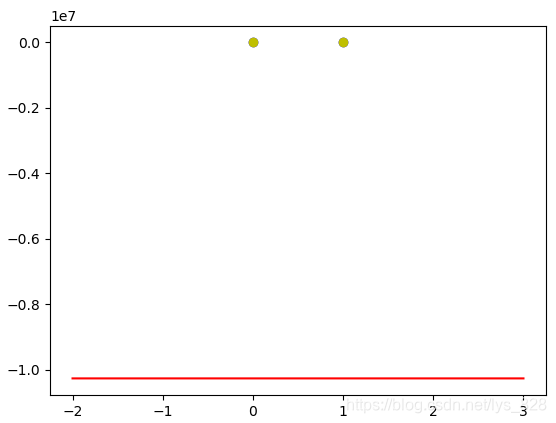
若标签是1，-1，且迭代1000次，输出结果为：（最终的结果是直线虽然没有办法进行正确的分类，始终是在四个点所在的区域内，而选择1,0标签则会导致直线越偏越远，这也就是为啥选择1，-1位标签的原因）
在这里插入图片描述
对于这种使用一条直线无法正确的对数据分类的问题，我们称作非线性问题，这也是线性网络的不足之处，为了解决这个问题，于是神经网络的研究又再进一步的发展，于是就有了其它的方法

4. $\delta$ 学习规则和梯度下降法

4.1 $\delta$ 学习规则

来源：1986年，认知心理学家McClelland和Rumelhart在神经网络训练中引入了 $\delta$ 规则，该规则也可以称为连续感知器学习规则。

$\delta$ 学习规则是一种利用梯度下降法的一般性的学习规则。学习规则的确定就离不开模型精度（误差判定），接下来就是介绍一下损失函数（也叫代价函数），英文名称为：Cost Function，Lost Function

二次代价函数(单个数据，如果是多个数据进行累加后求平均)：
$\frac{1}{2}(t-y)^{2} = \frac{1}{2}([t- f(XW)])^{2}$ 误差 $E$ 代表着网络模型的误差

4.2 梯度下降法

由上面的二次代价函数可知， $t$ 为标签值， $X$ 为输入节点数据，均为常数，而只有 $W$ 权重是变量，因此想要是的误差 $E$ 最小，就得改变 $W$ 的大小。而梯度下降法就是用来求解最小化 $E$ 的值

梯度下降法具体的方式就是：对 $E$ 求 $W$ 的导数，然后取导数的反方向，最后乘上学习率

$\Delta W = -\eta E^{'} = \eta X^{T}(t-y)f^{'}(XW) = \eta X^{T}\delta$ $\Delta w_{i} = -\eta E^{'} = \eta x_{i}(t-y)f^{'}(XW) = \eta X_{i}\delta$

注意第一个式子，是矩阵表示的形式，因此要对 $f (X W)$ 求导，提出来的 $X$ 应该是转置的，而第二个式子不是用矩阵表示的形式则不需要

图示法解析梯度下降法：（一维情况）

首先根据数学知识，二次代价函数与 $W$ 的图像是一个抛物线，开口是向上的（开口方向的确定是有 $W$ 二次项系数正负决定的，这里的是正的，所以开口朝上）
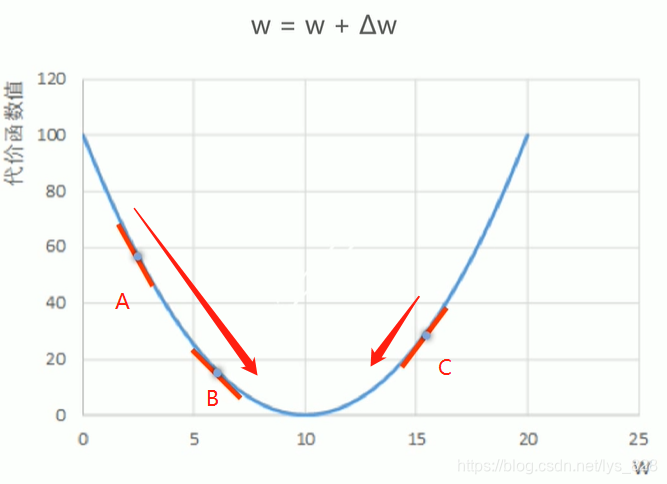
在这里插入图片描述
通过图形，可以发现，在最低点左侧的A到B两点的导数均为负值，然后再取导数的反方向，最终 $\Delta W$ 值为正，经过权值更新后向右移动，而C点处导数为正，取反方向就是为负，最终 $\Delta W$ 值为负，经过权值更新后向左移动，所以梯度下降法最终都会导致 $W$ 往 $E$ 的最小值方向移动

图示法解析梯度下降法：（二维情况）
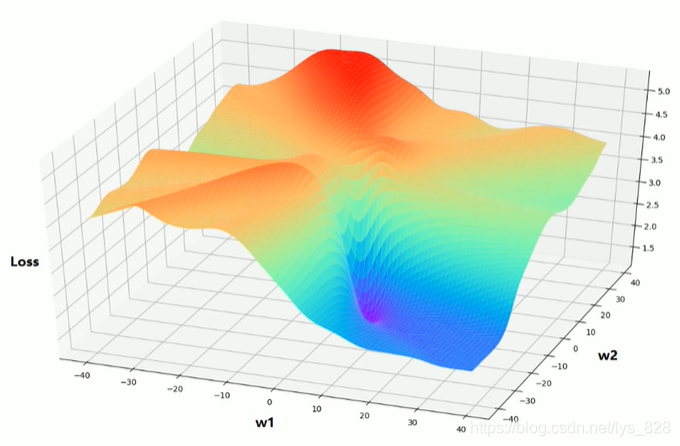
在这里插入图片描述
也是会按照导数相反的方向进行移动，最后取得“最小值”，注意这里的“最小值”在二维的时候就有可能是局部的“最小值”（局部极小值），而不是全局“最小值”

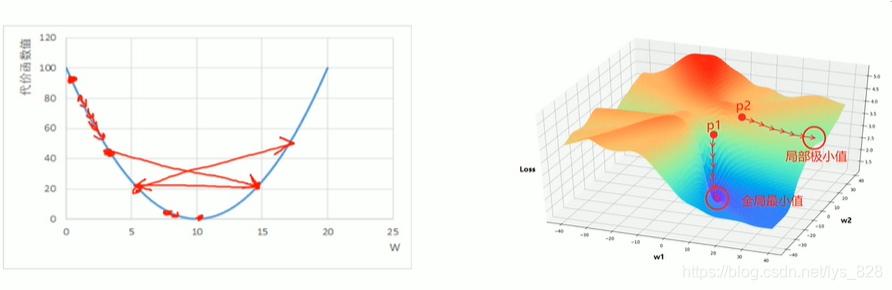
所以梯度下降法的问题：

学习率难以选取，太大会产生震荡，太小收敛缓慢（下面的左侧图）
容易陷入到局部最优解，也就是局部极小值（下面的右侧图）

在这里插入图片描述

5. BP神经网络介绍及详细推导

5.1 BP神经网络介绍

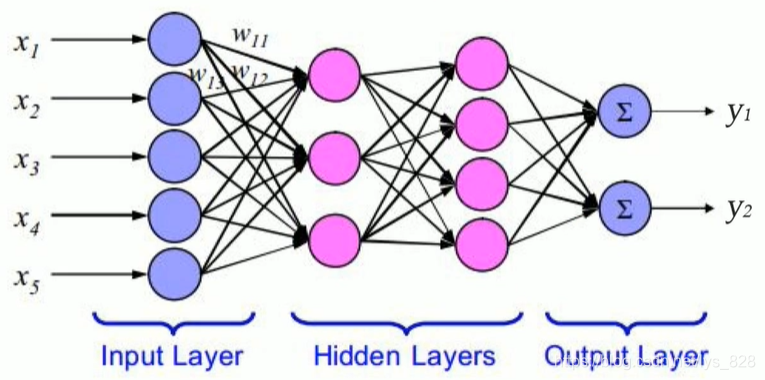
以上介绍的是单层感知器，也就是而输入层和输出层是直接相连的。相较于单层感知器，多层感知器输出端从一个变到了多个；输入端和输出端之间也不光只有一层，现在又两层：输出层和隐藏层。

1986年，由McClelland和Rumelhart为首的科学家小组在《 $P a r a l l e l D i s t r i b u t e d P r o c e s s i n g$ 》一书中，对具有非线性连续转移函数的多层感知器的误差反向传播( $e r r o r b a c k p r o r a g a t i o n$ , 简称 $B P$ ) 算法进行详尽的分析，解决了多层神经网络的学习问题，极大促进了神经网络的发展。由于多层感知器的训练经常采用误差啊反向传播算法，人们也常将多层感知器直接成为 $B P$ （神经）网络

BP神经网络也是整个人工神经网络体系中的精华，广泛应用于分类识别，逼近，回归，压缩等领域。在实际应用中，大约80%的神经网络模型都采取了BP网络或BP网络的变化形式。

在多层感知器的应用中，单隐藏层网络的应用较为普遍。一般习惯将单隐层感知器称为三层感知器，所谓的三层即是包含了输入层（ $I n p u t L a y e r$ ）、隐含层（ $H i d d e n L a y e r s$ ）和输出层（ $O u t p u t L a y e r$ ），其中从单词拼写中就可以发现隐藏层可以是多个，如下有两个隐藏层的多层感知器
在这里插入图片描述

5.2 BP神经网络的推导

5.2.1 参数说明

这里以三层感知器为例也就是，如下的网络结构
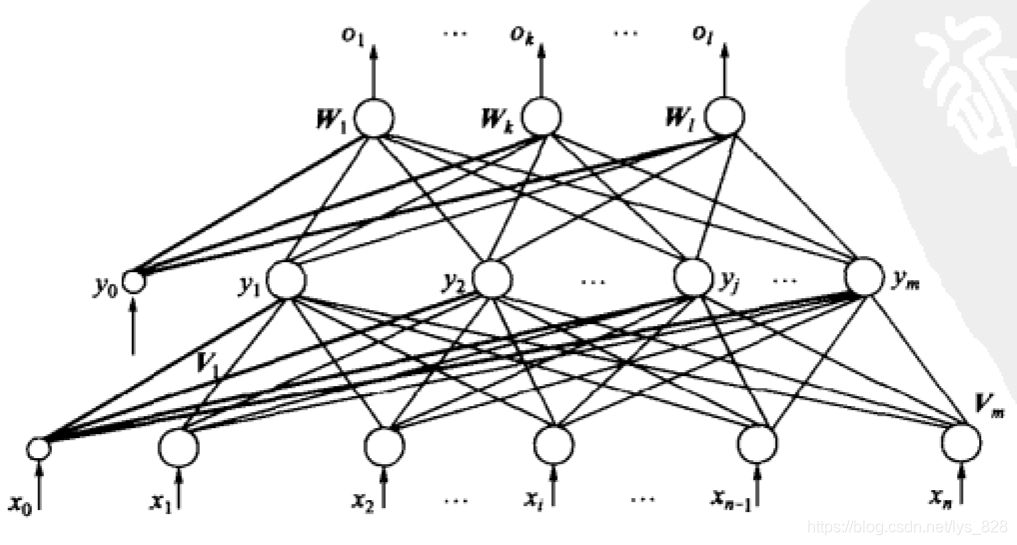
在这里插入图片描述
参数说明：

输入向量为 $X = (x_{1},x_{2},...,x_{i},...,x_{n})^{T}$ ，图中 $x_{0} = -1$ 是为了隐藏层神经元引入阈值而设置的
隐藏层输出向量 $Y= (y_{1},y_{2},...,y_{j},...,x_{m})^{T}$ ，图中 $y_{0} = -1$ 是为了输出层神经元引入阈值而设置的
输出层输出向量为 $O = (o_{1},o_{2},...,o_{k},...,o_{l})^{T}$
期望输出向量为 $d = (d_{1},d_{2},...,d_{k},...,d_{l})^{T}$
输入层到隐藏层之间的权值矩阵用 $V$ 表示， $V =V_{1},V_{2},...,V_{j},...,V_{m}$ ，其中列向量 $V_{j}$ 为隐含层第 $j$ 个神经元对应的权向量
隐含层到输出层之间的权重矩阵使用 $W$ 表示， $W=(W_{1},W_{2},...,W_{k},...,W_{l})$ ，其中列向量 $W_{k}$ 为输出层第 $k$ 个神经元对应的权向量

由于 $B P$ 神经网络是基于误差反向传播的，那么首先应该看的就是输出层

$o_{k} = f(net_{k}), k=1,2,...,l$
$net_{k} = \sum_{j=0}^{m}w_{jk}y_{j}, k=1,2,...,l$

其次对于隐含层，有：

$y_{j} =f(net_{j}), j=1,2,...,m$
$net_{j} = \sum_{i=0}^{n}v_{ij}x_{i}, j=1,2,...,m$

对于隐含层和输出层，激活函数 $f (x)$ 均为 $S i g m o i d$ 函数： $\frac{1}{1+e^{-x}}$ ， $f (x)$ 具有连续、可导的特点，且有： $f^{'} (x) = f (x) [1 - f (x)]$

5.2.2 误差与权值调整

当网络输出与期望（标签）输出不相等时，存在输出误差 $E$ ，前面已经介绍过二次代价函数，为了和图示的符号保持统一，这里将式子表达为：(只是修改一下符号) $\frac{1}{2}(d-O)^{2} = \frac{1}{2}\sum_{k=1}^{l}(d_{k}-o_{k})^{2}$ 将输出层的公式进行代入，结果为： $\frac{1}{2}\sum_{k=1}^{l}(d_{k}-f(net_{k}))^{2}=\frac{1}{2}\sum_{k=1}^{l}(d_{k}-f(\sum_{j=0}^{m}w_{jk}y_{j}))^{2}$ 再将隐藏层的公式进一步代入求解： $=\frac{1}{2}\sum_{k=1}^{l}(d_{k}-f(\sum_{j=0}^{m}w_{jk}f(net_{j}))^{2}=\frac{1}{2}\sum_{k=1}^{l}(d_{k}-f(\sum_{j=0}^{m}w_{jk}f(\sum_{i=0}^{n}v_{ij}x_{i}))^{2}$ 由此式可以看出，网络误差是各层权值 $w_{jk},v_{ij}$ 的函数，因此调整权值可以改变误差 $E$ ，根据梯度下降的原则，即： $\Delta w_{jk} = -\eta \frac{\partial E}{\partial w_{jk}}, j = 0,1,2,...,m; k=1,2,...,l$ $\Delta v_{jk} = -\eta \frac{\partial E}{\partial v_{ij}}, i= 0,1,2,...,n; j=1,2,...,m$

5.2.3 三层BP算法推导

① 假设

下面推导三层BP算法权值调整的计算式。首先约定，在全部推导过程中，对输出层均有 $\quad k=1,2,...,l$ ，对隐藏层均有 $\quad j=1,2,...,m$ （先声明一下，之后的式子后面就不用再写长长的取值范围了）

② 确定权值更新的公式

对于输出层，进一步求偏导，可得： $\Delta w_{jk} = -\eta \frac{\partial E}{\partial w_{jk}}=-\eta \frac{\partial E}{\partial w_{net_{k}}}\frac{\partial net_{k}}{\partial w_{jk}}$

对于隐藏层，也可进一步求偏导，可得： $\Delta v_{ij} = -\eta \frac{\partial E}{\partial v_{ij}}=-\eta \frac{\partial E}{\partial v_{net_{j}}}\frac{\partial net_{j}}{\partial v_{ij}}$

结合输出层和隐藏层，可以发现两者展开后存在相似之处，为了简化表达，不妨令 $\delta_{k}^{o} = -\frac{\partial E}{\partial w_{net_{k}}},\quad \delta_{j}^{y} = -\frac{\partial E}{\partial w_{net_{j}}}$ 。最终式子可以化简为： $\Delta w_{jk} = -\eta \delta_{k}^{o}y_{j}$ $\Delta v_{ij} = -\eta \delta_{j}^{y}x_{i}$ 由此可见只有计算出这两个式子的结果，也就可以得到更改的权值了，那么权值调整计算的推导也就完成了。于是，接下来关键就是 $\delta_{k}^{o}$ 和 $\delta_{j}^{y}$ 的求解了。

③ 偏导数求解一

对于输出层： $\delta_{k}^{o}=-\frac{\partial E}{\partial w_{net_{k}}}=-\frac{\partial E}{\partial o_{k}}\frac{\partial o_{k}}{\partial w_{net_{k}}}=-\frac{\partial E}{\partial o_{k}}f'(net_{k})$

对于隐藏层： $\delta_{j}^{y}=-\frac{\partial E}{\partial w_{net_{j}}}=-\frac{\partial E}{\partial y_{j}}\frac{\partial y_{j}}{\partial w_{net_{j}}}=-\frac{\partial E}{\partial y_{j}}f'(net_{j})$

③ 偏导数求解二

下面就该求解网络误差对于各层中的偏导了

对于输出层： $\frac{\partial E}{\partial o_{k}} = -(d_{k}-o_{k})$ 对于隐藏层： $\frac{\partial E}{\partial y_{j}}=-\sum_{k=1}^{l}(d_{k}-o_{k})f'(net_{k})w_{jk}$

④ 结果回代

将计算的结果重新带回 ③ 偏导数求解一 中得： $\delta_{k}^{o}=(d_{k}-o_{k})o_{k}(1-o_{k})$ $\delta_{j}^{y}=(\sum_{k=1}^{l}(d_{k}-o_{k})f'(net_{k})w_{jk})f'(net_{j})=(\sum_{k=1}^{l}\delta_{k}^{o}w_{jk})y_{j}(1-y_{j})$

最后就是将上面的结果代回到 ② 确定权值更新的公式 中，得到： $\Delta w_{jk} = -\eta \delta_{k}^{o}y_{j}=\eta (d_{k}-o_{k})o_{k}(1-o_{k})y_{j}$ $\Delta v_{ij} = -\eta \delta_{j}^{y}x_{i}=\eta (\sum_{k=1}^{l}\delta_{k}^{o}w_{jk})y_{j}(1-y_{j})x_{i}$

5.2.4 归纳延伸

上面对三层 $B P$ 算法进行了推导，那么接下来将其推广到多层。对于一般多层感知器，设共有 $h$ 个隐藏层，按前后顺序各隐藏层节点个数为 $m_{1},m_{2},m_{3},...m_{h}$ ，各隐藏层输出分别即为 $y_{1},y_{2},y_{3},...y_{h}$ ，各层的权值矩阵分别为 $W^{1},W^{2},W^{3},...W^{h},W^{h+1}$ ，则各层权值调整的计算公式为：

输出层： $\Delta w_{jk}^{h+1}= -\eta \delta_{k}^{h+1}y_{j}^{h}=\eta (d_{k}-o_{k})o_{k}(1-o_{k})y_{j}^{h},\quad j=0,1,2,...,m_{h}, k=1,2,...,l$ 第h隐藏层： $\Delta w_{ij}^{h}=\eta \delta_{j}^{h}y_{i}^{h-1}=\eta (\sum_{k=1}^{l}\delta_{k}^{o}w_{jk}^{h+1})y_{j}^{h}(1-y_{j}^{h})y_{i}^{h-1},\quad i=0,1,2,...,m_{h-1},j=1,2,...,m_{h}$ 按照以上规律组成类推，则第一隐藏层权值调整计算公式为： $\Delta w_{pq}^{1}=\eta \delta_{q}^{1}x_{p}=\eta (\sum_{r=1}^{m_{2}}\delta_{r}^{2}w_{qr}^{2})y_{q}^{1}(1-y_{q}^{1})x_{p},\quad p=0,1,2,...,n,j=1,2,...,m_{1}$

5.3 三层感知器的BP算法的向量形式

根据上面的求解，对于输出层：设 $Y=(y_{0},y_{1},y_{2},...y_{j},...y_{m})^{T}$ ， $\delta^{o} =(\delta^{o}_{1},\delta^{o}_{2},...\delta^{o}_{k},...\delta^{o}_{l})^{T}$ ，则： $\Delta W= \eta(\delta^{o}Y^{T})^{T}$ 对于隐藏层：设 $X=(x_{0},x_{1},x_{2},...x_{i},...x_{n})^{T}$ ， $\delta^{y} =(\delta^{y}_{1},\delta^{y}_{2},...\delta^{y}_{j},...\delta^{y}_{m})^{T}$ ，则： $\Delta V= \eta(\delta^{y}X^{T})^{T}$ 可以看出， $B P$ 学习算法中，各层的权值调整公式形式上都是一样的，均由3个因素决定，即：学习率 $\eta$ ，本层输出的误差信号 $\delta$ ，以及本层输入信号 $Y$ (或者 $X$ )。其中输出层误差信号与网络的期望输出和实际输出之差有关，直接反映了输出误差，而各隐藏层的误差信号与前面各层的误差信号都有关，是从输出层开始逐层传递过来的。

6 BP算法的公式小结

二次代价函数： $\frac{1}{2}(t-y)^2$
$\delta^{l}=\delta^{l+1}(W^{l+1})^{T}f'(X^{l}W^{l})$ $\quad\delta^{l}:$ 第 $l$ 层的学习信号， $W^{l}:$ 第 $l - l + 1$ 层权值
$\delta^{L}=(t-y)f'(X^{L}W^{L})$ $\quad\delta^{L}:$ 输出层的学习信号， $X^{l}：$ 第 $l$ 层输出信号
$\delta$ 学习规则: $\frac{\partial E}{\partial W^{l}} = -(X^{l})^{T}{\delta^{l}},\qquad \Delta W^{l}=-\eta\frac{\partial E}{\partial W^{l}}=\eta(X^{l})^{T}{\delta^{l}}$