【算法笔记】计算几何之向量

前言

本来想写一篇计算几何的博客，没想到写不完了，那就写完向量吧

向量

有大小有方向的量。

向量可以理解为空间中的箭头，自一点出发，指向另一点，在数学中，向量的起始点一般是坐标原点。

因此向量可以用一个点表示（从原点指向那个点的向量）

如$(3,5)$表示从$(0,0)$起始，指向$(3,5)$的一个箭头。

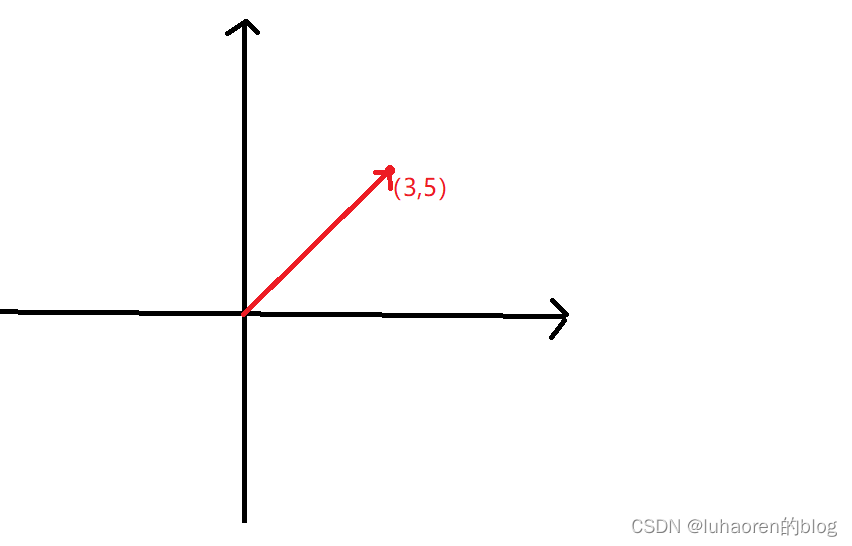
向量也可以理解为一个点的位移，如上图的向量即可理解为从$(0,0)$移动到$(3,5)$

在OI中，向量一般用一个点$(x,y)$表示，方便进行叉积等计算。

struct Vec{
   
   
	double x,y;//向量结构体
};

向量的模长

刚刚说过向量是一条箭头，模长就是箭头的长度。

若$A(x,y)$，则$|A|=\sqrt{x^2+y^2}$

struct Vec{
   
   
	double x,y;//向量结构体
	double len(){
   
   
		//返回模长
		return sqrt(x*x+y*y);
	}
};

向量的加法

如有两个向量$A$和$B$，分别表示从$(0,0)$移至$(1,2)$和从$(0,0)$移至$(3,1)$。

那么$A+B$表示什么呢？

表示先从$(0,0)$位移至$(1,2)$，再以$(1,2)$为坐标原点，移动到$(3,1)$（在新的坐标系里就是$(4,3)$），而这个过程中的位移是 ( 4 , 3 ) (4,3)