Ivan the Fool and the Probability Theory（思维+dp）

题目链接

题目大意
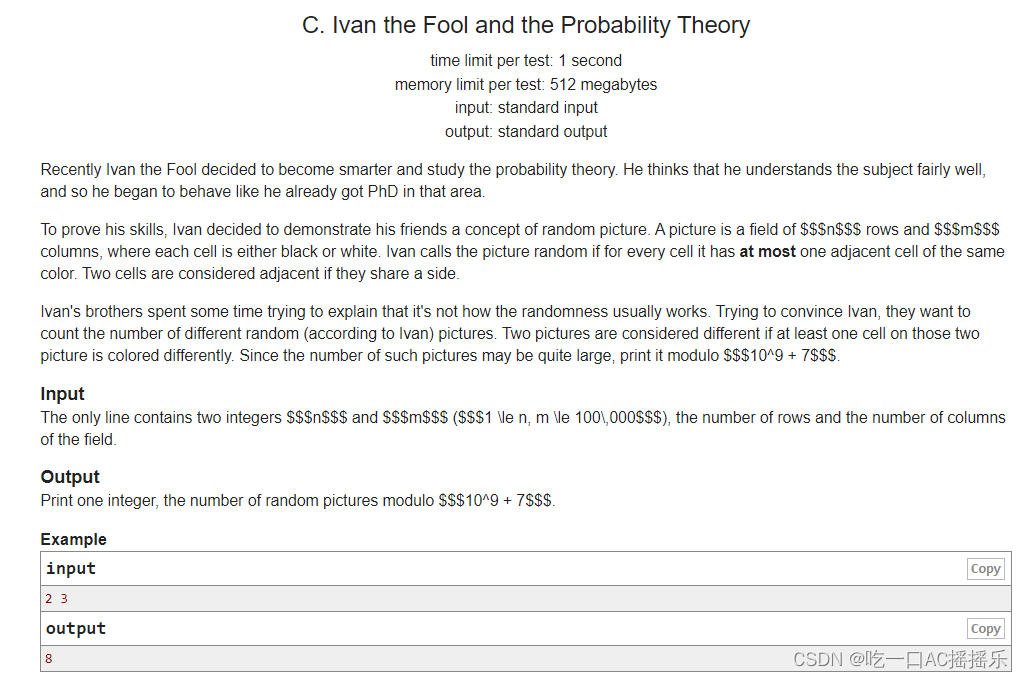
给定一个 $n\ast m$ 的方格图，每个格子可以被染成黑色或白色，且与其相邻的格子（上，下，左，右）中至多只有一个与其颜色相同。求方案数。

思路：
这个时候大家自己画一画就发现了一个规律：相邻两行的格子颜色要么完全相同，要么完全相反。

如果上面一行有两个连续相同的白色或者黑色，这个时候每一行的颜色就确定了，下一行的颜色一定与上面一行相反，所以第一行有多少种两个连续相同的颜色排法，那么就有多少种整体排法；

反之，如果上面一行没有两个连续相同的颜色，那么下一行的颜色一定为黑白相间，所以此时每行的颜色排放由每行第一列的颜色决定，即整体的排法等于第一列颜色的排法；

综上所述，整体的颜色就为$(2\ast dp[n]+2\ast dp[m]-2)$

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 1e6+10;
const int mod = 1e9 + 7;
string s;

ll ans;
ll ans1, ans2;
map<int, int>cnt;	
ll f[N];
int main() {
    int n, m;
    cin >> m >> n;
    f[1] = f[0] = 1;
    for (int i = 2; i <= max(n, m); i++)
        f[i] = (f[i - 1] + f[i - 2]) % mod;
    ll ans = ((f[n] + f[m] - 1) % mod) * 2 % mod;
    cout << ans << endl;

}