CF 1567 C. Carrying Conundrum（思维）-优快云博客

这篇博客探讨了一道有趣的数学问题，描述了一个小孩在做加法时错误地将进位加到了错误的位置。文章通过分析指出，只有相差2的数之间会有进位，并提供了计算不同组合数量的方法。最终，博主给出了计算正确结果的代码实现，并指出在计算总数时需要排除全为0的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

CF 1567 C. Carrying Conundrum（思维）

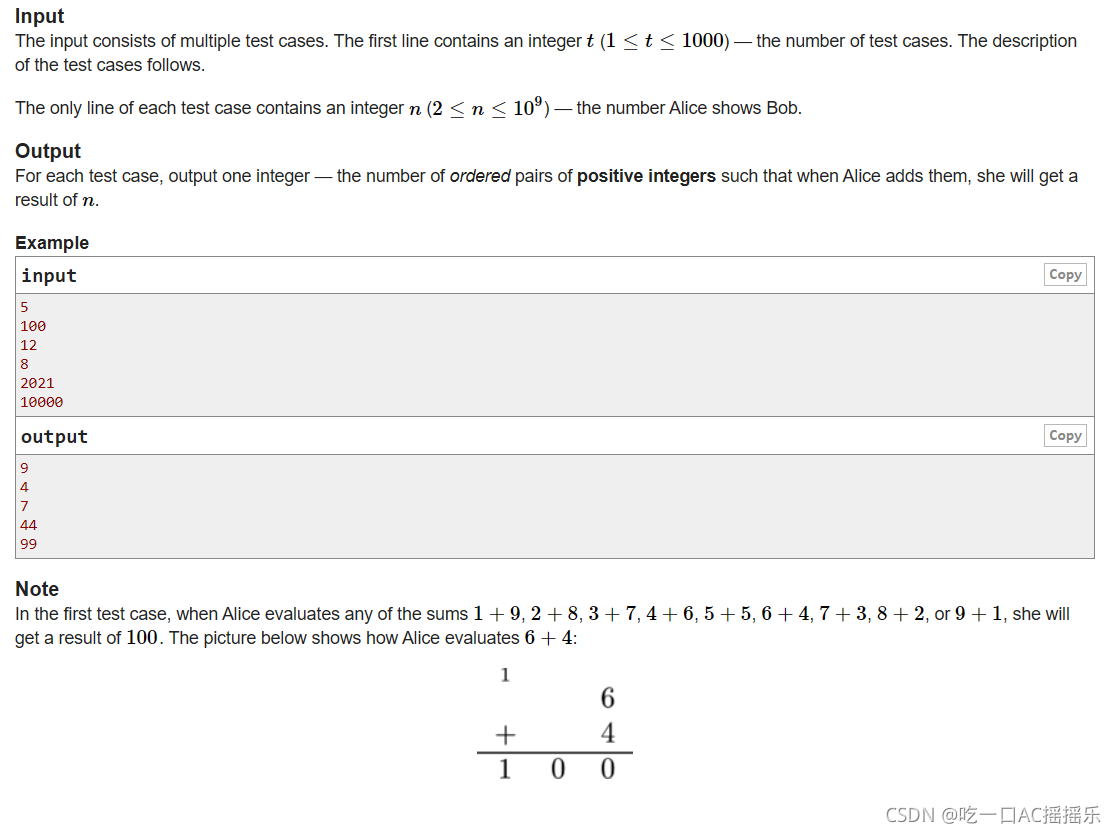
在这里插入图片描述

题目大意：

题目大意很有意思，就是一个小孩他不会列式相加，把进位加到了该位左侧的第二位上，现在给出结果，问按照这个小孩的方法，能有多少种情况使得两数之和等于所给的数，需要注意的是，两数只要不相同就算一种情况。

思路：

对于每一个数，我们将其的奇偶位分别取出，因为只有相差为 $2$ 的位之间才有进位关系，其次，对于奇数位所取出的数以及偶数位来说，凑出这两种数的情况就有他自身大小加一种情况（若一个数为 $n$ ，则两数相加为 $n$ 有 $n + 1$ 种情况，即 $0 + n, 1 + n - 1 . . . . n - 1 + 1, n + 0$ ）。
两数相乘即为答案，但是我们注意到，在组成两种数的情况中，可能会出现全为0的情况奇偶各一种所以答案要减去2.

#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
#define pi 3.1415926535
#define me(a,b,c) memset(a,b,sizeof c)
#define eps 0.00000001
//#define x first
//#define y second

using namespace std;

typedef long long ll;
const int mod = 1e9 + 7;
typedef pair<int, int> pii;

const int N = 1e6 + 10;
const int P = 131;
typedef unsigned long long ULL;
char s[N];
int main()
{
	int t;
	cin >> t;
	while (t--)
	{
	
		cin >> s+1;
		int n = strlen(s + 1);
		reverse(s + 1, s + 1 + n);
		ll odd = 0, even = 0;
		ll h = 1;
		ll k = 1;
		for (int i = 1;i <= strlen(s+1); i++) {
			if (i % 2)odd += (s[i] - '0') * h,h*=10;
			else even += (s[i] - '0') * k,k*=10;
			
		}
		odd++;
		even++;
		ll ans = (odd * even) - 2;
		cout << ans << endl;
	}
}
//                            _ooOoo_
//                           o8888888o
//                           88" . "88
//                           (| -_- |)
//                           O\  =  /O
//                        ____/`---'\____
//                      .'  \|     |//  `.
//                     /  \|||  :  |||//  \
//                    /  _||||| -:- |||||-  \
//                    |   | \\  -  /// |   |
//                    | \_|  ''\---/''  |   |
//                    \  .-\__  `-`  ___/-. /
//                  ___`. .'  /--.--\  `. . __
//               ."" '<  `.___\_<|>_/___.'  >'"".
//              | | :  `- \`.;`\ _ /`;.`/ - ` : | |
//              \  \ `-.   \_ __\ /__ _/   .-` /  /
//         ======`-.____`-.___\_____/___.-`____.-'======
//                            `=---='
//        ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
//
//             Buddha blesses the code with no bugs
// 1 2 3 4 5 6 7 8 9
// 0 1 3 0 4 1 7 0