基于混沌映射的医学图像加密

基于流密码增强逻辑映射的医学图像加密方法与安全分析

1. 引言

起初，医学图像加密技术与密码学理论紧密相关，随后新理论的引入丰富了其自身体系，并相继出现了基于密码学理论和混沌映射的重要加密方法。从实际效果来看，基于混沌映射的图像加密技术具有更高的安全性和抗攻击能力，是当前主流的图像加密方法[1,2]。密码学理论也对图像信息的加密具有良好的对应性。通过加密处理，医学图像信息能够得到更好的保护。

现代密码学的研究可以追溯到20世纪40年代末，其创始人是世界著名科学家香农。香农密码学的基本思想是将原始信息以某种规律转换成明文，从而使明文信息无法表达真实内容完全保留原始信息的含义，以避免攻击。早期的信息加密技术，其思想源于香农理论[3]。

对于图像加密技术，可以从图像中提取像素数据，形成由图像灰度数据组成的原始信息比特流，然后根据香农密码学理论的一般方法对原始信息进行加密。该领域有许多代表性方法，例如DES图像加密技术、AES图像加密技术[4,5]。这些加密方法成功的关键在于，用于加密的密钥不能被攻击者获知，同时接收者能够准确获取该密钥。

在20世纪末，混沌理论开始应用于图像加密技术领域。这一应用源于混沌理论在密码学领域的应用，而密码学本身就是图像加密技术的支撑技术之一，这直接促成了混沌理论在图像加密技术中的实用性。基于混沌的图像加密技术分为两个分支：一是基于流密码的图像加密，二是基于分组密码的图像加密[6,7]。

在基于流密码的图像加密领域，各种混沌映射被广泛用于生成控制加密过程的随机密钥流。该密钥流通过与普通图像像素进行逻辑运算，形式上获得密文的关键因素。在这方面，已应用的混沌映射包括逻辑映射、分段线性映射等。从形式上看，这些映射均为低维混沌映射。普拉文库马尔构建的图像加密系统基于逻辑映射，但其弱点在于抗攻击能力不明显[8]。

在低维混沌加密方法效果不佳的情况下，二维混沌映射被引入到图像加密领域。例如，利用二维混沌映射实现像素矩阵置乱是一种典型的方法。在此基础上，一些学者进一步采用扩散等手段改变原始图像的直方图信息，并进行多次扩散以提高加密图像信息的安全性能[9]。博特林将一维混沌映射与二维混沌映射相结合，通过二维混沌映射实现像素矩阵置乱，通过一维混沌映射设置控制码流，在一定程度上提升了图像加密的效果[10]。

本文以图像加密技术为研究对象，通过混沌理论对现有的图像加密技术进行改进或重新设计，从而从流密码方式构建一种高性能医疗图像加密方法。

2. 流密码加密中的密钥生成

从国内外研究现状的分析可以看出，基于混沌理论的图像加密技术分为两个分支：一种是基于流密码的混沌加密，另一种是基于分组密码的混沌加密。本章主要研究基于流密码的混沌加密技术。

基于流密码实现混沌加密有两种方式：一种是利用混沌理论构建加密过程的流密码，另一种是利用混沌理论构建伪随机数生成器[11]。根据经验，一般的同步系统无法对系统参数的变化做出准确响应，因此难以直接用作密码。混沌理论解决了这一问题。在混沌理论系统下，系统的伪随机性能优异[12]。同时，其轨道特性的多样性以及对初始状态的敏感性特别适用于图像加密技术。从现有结果来看，该流

基于混沌理论的密码加密技术具有较强的抗攻击能力和良好的实时性能。

在基于流密码的混沌加密方法构建中，如何生成密钥是实际加密过程的关键。利用混沌理论获得一组随机数并不困难，但在图像加密中，数值通常为整数，因此通过混沌理论得到的随机数必须进行量化。将非整数量化为整数的方法有很多，我们需要做的是为图像加密选择合适的方法。以下是对几种典型的基于混沌理论获取二进制数的方法的分析。

2.1 基于混沌理论获取二进制数的第一种方法

使用混沌映射可使加密结果更加均匀地置乱。假设一个混沌映射满足以下条件：

$$
w_{n+1} = r(w_n) \tag{1}
$$

其中，$ w_n = r^n(w_0) \in I, n = 0, 1, 2, \cdots $，同时，$ r^n(\cdot): I \rightarrow I $ 表示一个一维混沌映射。

为了获得二进制数，给出一个简单的判别函数，其数学描述如公式(2)所示。

$$
\theta_t(w) =
\begin{cases}
0 & w < t \
1 & w > t
\end{cases} \tag{2}
$$

这里，$ w $ 是一个变量，而 $ t $ 是一个阈值。

公式（2）中给出的函数的补码状态描述如下：

$$
\bar{\theta}_t(w) = 1 - \theta_t(w) \tag{3}
$$

根据上述步骤，我们最终可以得到二进制随机数集合 ${\theta_t(r^n(w))}_{n=0}^{\infty}$。

2.2. 基于混沌理论获取二进制数的第二种方法

该方法的思想是首先将混沌处理值进行二进制化，如公式(4)所示。

$$
|w| = 0, A_1(w), A_2(w), \cdots A_i(w) \in {0, 1} \tag{4}
$$

其中 $ A_i(w) $ 表示二进制数中的一个比特位。其数学描述如下:

$$
A_i(w) = \sum_{r=1}^{2^{t}-1} (-1)^{r-1} \left{ \theta_{\frac{r}{2^t}}(w) + \bar{\theta}_{-\frac{r}{2^t}}(w) \right} \tag{5}
$$

经过公式(4)和(5)处理后，可得到一组二进制随机数 ${A_i(w)}_{n=0}^{\infty}$。其中，$\theta_t(w)$ 表示一个以 $ w $ 为计算种子的布尔函数。这样，公式(5)可进一步改写为：

$$
A_i(w) = \oplus_{r=1}^{2^l} \left{ \theta_{\frac{r}{2^t}}(w) \oplus \theta_{-\frac{r}{2^t}}(w) \right} \tag{6}
$$

2.3. 基于混沌理论获取二进制数的第三种方法

这是一种基于一维切比雪夫映射的伪随机数生成方法。切比雪夫映射的数学描述如公式(7)所示。

$$
x(n+1) = \cos{w \cdot \arccos[x(n)]} \tag{7}
$$

在生成二进制数集的过程中，该映射所使用的判别公式如下：

$$
\theta_{0.5}(x(n)) =
\begin{cases}
0 & x(n) < 0.5 \
1 & x(n) > 0.5
\end{cases} \tag{8}
$$

一些学者指出，混沌映射生成的伪随机数集存在一些问题，因为数字信息（包括数字图像）的处理设备（如计算机）由于自身周期性规律，会对混沌映射的相关计算带来周期性影响，从而破坏其随机特性。此外，在生成随机数序列时，很难识别其随机特性。

因此，学者们从科学角度构建了相应的方法来解释一组随机数的随机特性。该理论体系为这组随机数设计了频率检验、序列检验、游程检验和相关性检验。

以游程检验为例，如果按照预设长度对随机数集进行分组，则可以检验随机数集中每组的频率，从而获得随机特性的检验结果。如果长度的设定值为0，游程检验变为频率检验；如果长度的设定值为1，游程检验变为序列检验。

3. 医疗图像加密方法的设计

3.1. 逻辑映射

逻辑映射是描述混沌的一种典型映射模型。由于其分岔图类似于虫洞，因此也称为虫洞模型。逻辑映射的基本数学描述模型如公式(9)所示。

$$
x_{n+1} = \mu x_n (1 - x_n) \quad \mu \in [0, 4] \tag{9}
$$

$$
x_n \in (0, 1), \quad n = 0, 1, 2, \cdots
$$

描述混沌映射的另一个重要方法是分岔图，如图1所示。从图1可以看出，在逻辑映射的 $ \mu = 3.569945 $ 处，系统开始从稳定状态进入混沌状态。3.569945 可被视为逻辑映射的混沌临界点。

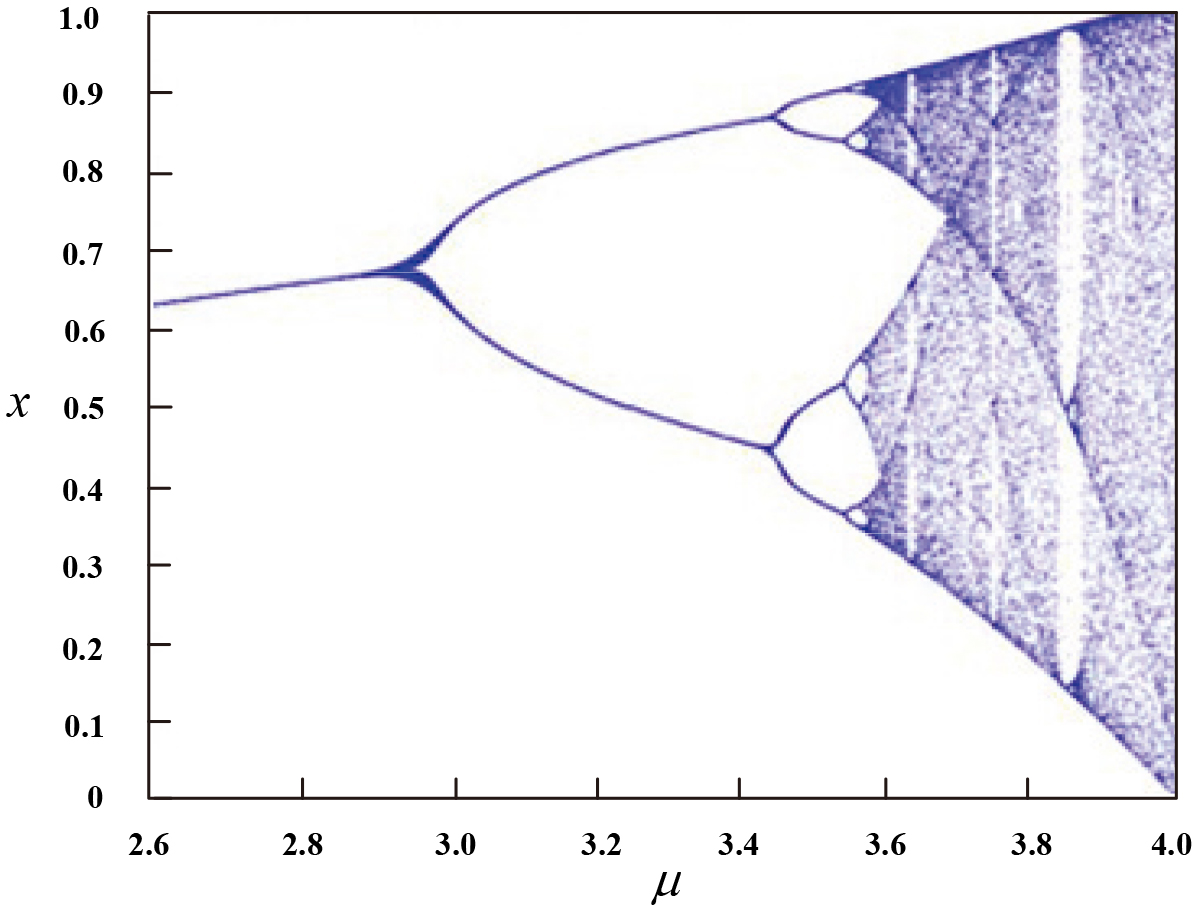
3.2. 密钥生成

本文根据流密码混沌加密的基本思想，利用逻辑映射构建了一种图像加密方法。首先介绍了该加密方法的密钥生成方式，该方式基于切比雪夫映射，并构造了两种不同形式的密钥。

第一个密钥按照十六进制进行分组，分为20组。每组信息的长度为4位，即 $ K = k_1 k_2 \cdots k_{20} $，$ k_i $ 表示一个十六进制数。

第二个秘密是根据ASCII码进行分组处理，将其分为10

3.3. 生成初始值

如前所述，由于混沌理论对初始状态和计算设备的处理精度非常敏感，因此以二进制数形式给出输入值的优势远大于以浮点数形式给出。在该方法的初始值设置中，分为以下步骤：

第一步 是选择密钥 $ K_4K_5K_6 $ 在ASCII码下用于初始值 $ X_{01} $ 生成，如公式(12)所示。

$$
B_1 = K_{41}K_{42} \cdots K_{48}K_{51}K_{52} \cdots K_{58}K_{61}K_{62} \cdots K_{68}
$$

$$
X_{01} = (K_{41} \times 2^0 + K_{42} \times 2^1 + \cdots + K_{48} \times 2^7 + K_{51} \times 2^8 + K_{52} \times 2^9 + \cdots + K_{58} \times 2^{15} + K_{61} \times 2^{16} + K_{62} \times 2^{17} + \cdots + K_{68} \times 2^{23}) / 2^{24} \tag{12}
$$

第二步 ，在十六进制码中选择 $ k_7k_8k_9 $ 以生成初始值，如公式(13)所示。

$$
X_{02} = \sum_{i=13}^{18} (k_i)_{10} / 96 \tag{13}
$$

第三步 是将初始值 $ X_{01} $ 和初始值 $ X_{02} $ 结合得到 $ X_0 = (X_{01} + X_{02}) \mod 1 $。

第四步 是从密钥 $ K_1K_2K_3 $ 中按ASCII码选取以生成初始值 $ Y_{01} $，如公式(14)所示。

$$
B_2 = K_{11}K_{12} \cdots K_{18}K_{21}K_{22} \cdots K_{28}K_{31}K_{32} \cdots K_{38}
$$

$$
Y_{01} = (B_2)_{10} / 2^{24} \tag{14}
$$

$$
Y_{02} = \left( \sum_{k=1}^{24} B_2[P_k] \times 2^{k-1} \right) / 2^{24}
$$

其中 $ P_k = \text{int}(23 \times X_{k-1} / 0.8) + 1 $。

第五步 是将式（14）中的初始值与初始值结合，得到 $ Y_0 = (Y_{01} + Y_{02}) \mod 1 $。经过以上五个步骤，混沌系统的初始值成功设置。考虑到解密过程的便利性，该区间跨度需要进一步细分，结果被划分为24个独立子区间，然后计划为八组。

3.4. 加密过程

在通过上一节中的方法获得图像加密密钥后，图像数据的加密过程如下：

首先 ，从图像像素矩阵中获取三个连续字节的图像信息。实际上，这三个字节的图像信息应分别代表一个像素的R、G和B值。

其次 ，第一个像素以值 $ Y_n $ 作为混沌加密迭代处理的入口，加密 $ n = (K_{10})_{10} $ 次，并连续加密16个像素。

第三 ，为了更新当前密钥数据信息，可以使用以下数学处理方法：

$$
(K_i) {10} = ((K_i) {10} + (K_{10})_{10}) \mod 256 \tag{15}
$$

第四 ，根据X和Y维度的逻辑映射，继续处理更新后的密钥数据以获得新的初始加密值，并对最后16个像素执行加密过程。

重复上述操作，直到图像中的所有像素数据都被加密。
组，每组信息长度为8位，即 $ K = K_1K_2 \cdots K_{10} $，$ K_i $ 表示ASCII码。

对于这两种密钥，选择了两个逻辑映射，其数学形式分别为公式(10)和(11)。

$$
X_{n+1} = 3.9999X_n(1 - X_n) \tag{10}
$$

$$
Y_{n+1} = 3.9999Y_n(1 - Y_n) \tag{11}
$$

4. 实验结果与分析

4.1. 医学图像加密视觉效果

为了验证本文构建的基于逻辑映射的图像加密方法的性能，对血细胞进行了加密实验。加密前的图像、加密后的图像以及解密后的图像如图2所示。

从图2中的实验结果可以看出，经过逻辑映射加密后图像的置乱效果仍然理想，而解密图像基本恢复了原始图像的真实信息。同时，原始图像的峰值信噪比为29.57，解密图像的峰值信噪比为29.62，充分说明了本文加密和解密方法的有效性。

4.2. 密钥敏感性评估

对于医学图像加密，密钥敏感性是评估加密算法质量的一个非常重要的指标。如果密钥发生轻微变化，就无法正确解密，这表明该加密方法具有较高的加密性能。相反，如果密钥发生较大变化，图像仍能部分解密，则表明该加密方法的加密性能较差。

本文中，分别对1比特密钥和2比特密钥进行修改，解密结果如图3所示。

从图3中的结果可以看出，本文方法加密的图像即使解密密钥发生轻微变化也无法正确解密。密钥的微小变化将导致解密结果错误。这也说明该方法的安全性能非常高。

4.3. 明文敏感性评估

明文敏感性是指明文的单像素变化对密文的影响。对于明文敏感性测试，通常选择NPCR测试标准。如果一幅图像的单个像素值发生变化，其对应的加密图像分别表示为 $ C_1 $ 和 $ C_2 $。

定义 $ D(i) $ 用于判断 $ C_1(i) $ 与 $ C_2(i) $ 之间的关系。当 $ C_1(i) $ 与 $ C_2(i) $ 相等时，将 $ D(i) $ 设为1，否则设为0。然后可以定义NPCR的判断标准公式如下。

$$
\text{NPCR} = \frac{\sum_i D(i)}{\text{size}(D)} \times 100\% \tag{16}
$$

将该标准应用于血细胞图像的加密测试，可以看出NPCR值高达0.9874，证明了该方法对明文变化的敏感性。

4.4. 所提出方法在磁共振成像图像上的结果

为了验证该方法的应用范围，将所提出的方法应用于磁共振成像图像加密处理，结果如图4所示。

从图4可以看出，对于MRI图像，加密后得到的加密图像仍然均匀地被扰乱。

5. 结论

为了解决医学图像加密的问题，本文提出了一种结合流密码和混沌理论的新加密方法。首先，根据流密码理论，使用切比雪夫映射生成加密密钥。其次，通过一系列编码操作设置图像混沌处理前的初始值。最后，结合逻辑映射，从X和Y维度对原始图像信息进行加密。在实验中，选择了一幅血细胞图像进行加密。结果表明，加密图像中的像素分布均匀。进一步的密钥敏感性评估证明，本文方法对密钥的微小变化非常敏感，加密安全性高。明文敏感性评估结果表明，加密血细胞图像的NPCR值高达0.9874。灰度直方图评估也证明了该加密方法具有较高的安全性。