基于LFSR与混沌的图像加密

基于线性反馈移位寄存器的多蚁胞自动机与基于混沌映射的图像加密

1 引言

如今，由于数据通信和网络技术的快速发展，多媒体数据（如视频、图像或其他重要信息）被越来越多地传输给多个用户。在某些应用中，图像通过在线网络或任何通信信道传输时，需要防止未授权用户访问。

图像加密是一种利用共享密钥将有意义（原始）图像转换为无意义（密文）图像的新技术，使得未经授权的用户难以从加密图像中恢复原始图像。通用密码原语在保护图像隐私方面发挥着至关重要的作用，例如公钥加密方案、流密码和分组密码。此外，图像加密具有广泛的应用，如保护地理卫星图像、网络上的在线数据传输、多媒体系统、生物医学成像以及军事通信中的敏感信息保护。

在过去的几十年中，已经实施了不同的图像加密方案。其中一些方案基于DES、AES和RSA密码系统。另一方面，图像具有大数据量、大量冗余数据以及实时性要求等基本特征。然而，鉴于图像信息量巨大，加密算法应当更加先进和高效。因此，传统加密方案在应对图像的一些关键特性（即大量数据、邻域像素间的高相关性以及大量冗余数据）时，似乎并不适用于图像加密。此外，大多数现有加密算法无法有效抵御攻击。为了消除此类攻击，加密方案中需要对像素进行充分的混淆。在此情况下，混沌映射在混合与整合像素特征方面起着至关重要的作用。受上述因素启发，本文提出一种新的图像加密方案，结合基于LFSR的多蚁细胞自动机与混沌映射。

所提出的方案利用兰顿蚂蚁元胞自动机的概念，通过线性反馈移位寄存器（LFSR）生成多个类型相似的蚂蚁。在此方法中，多个蚂蚁同时朝特定方向移动，

由可视为随机数生成器的线性反馈移位寄存器（LFSR）进行控制。图像的坐标位置随着蚂蚁的每次移动而改变，这些坐标位置即为图像的像素位置。利用密钥和混沌系统来改变图像每个像素的灰度值，从而得到密文图像。在图像解密过程中，使用相同的密钥、混沌系统和LFSR来恢复原始图像。NPCR（像素变化率）和UACI（归一化平均变化强度）是从统计角度验证该加密方案能否抵御选择明文攻击的两个重要因素，这两个指标的测量值接近理想值。

1.1 本研究的贡献

本研究提出了一种图像加密技术，本文的贡献如下：
1. 线性反馈移位寄存器（LFSR）用于生成非连续数字列表，该列表被视为伪随机序列。
2. 基于线性反馈移位寄存器的兰顿蚂蚁元胞自动机概念被用来创建类似类型的多个蚂蚁，这些蚂蚁可以并行地运行。由于能够并行运行，计算成本低于单个兰顿蚂蚁元胞自动机概念。利用兰顿蚂蚁元胞自动机概念，图像在较短时间内被置乱。
3. 对所提出的方案进行了统计分析，包括直方图、信息熵、密钥敏感性、明文图像敏感性以及两个相邻像素的相关性。我们的方案的NPCR结果优于其他现有方案。

1.2 本文结构

第2节回顾了一些现有的相关方案。第3节讨论了预备知识，以引出我们提出的方案。我们在第4节介绍了所提出的方案。第5节对所提出的方案进行了分析评估。第6节将所提出方案的性能与现有相关方案进行了比较。最后，本工作的结论在第7节中给出。

2 文献综述

王和徐¹提出了一种基于兰顿蚂蚁元胞自动机概念的方案，其中蚂蚁在四个方向（即上、下、左、右）移动，蚂蚁的移动由交织逻辑映射控制。该研究¹根据蚂蚁在每一时刻所处的位置，确定原始图像像素在置乱图像中的位置。此外，参考文献¹中的方案使用分段线性混沌映射来扩散图像。

乌拉姆和冯·诺依曼⁹提出了细胞自动机的概念，其中定义了具有预定义规则的网格。每个网格被视为一个细胞，每个细胞具有特定状态。根据一些预定义规则，每个细胞在网格中改变其状态。此处，细胞自动机可以实现为一维、二维或多维。

高和陈¹⁰和Chen提出了一种新的图像加密方案，其中他们创建了一个矩阵来打乱图像像素，然后使用超混沌系统来随机化原始图像与密文图像之间的关系。

Sun等人¹¹展示了一种方案，其中使用了空间混沌系统。在此方案中，像素通过空间混沌系统进行映射，并在空间的多个方向上混淆像素位置。利用此过程，由于混沌系统的固有特性，图像在空间上变得不可分割。

Salah等人¹²提出了一种基于LFSR的彩色图像加密方案。在此方案中，LFSR用于生成打乱图像像素位置的随机数。这些随机数用于沿行重新排列像素位置，然后沿列重新排列像素。

Chai¹³提出了一种方案，其中使用SHA 256哈希值来生成混沌系统的初始值和系统参数，以混淆和扩散原始图像。基于布朗运动，对像素位置进行置乱。采用双向扩散过程沿行和列扩散图像。整个过程重复多轮以获得更好的结果。

Chen 等人¹⁴提出了一种使用渐进式细胞自动机替换来替换像素值的方案。该细胞自动机替换过程实现了图像加密所需的混淆和扩散特性。该方案¹⁴由于具有大量的密钥而具有很高的安全性。

Wang 等人¹⁵提出了一种基于二维细胞自动机的新型图像加密模型。该细胞自动机概念实现了用于图像加密的不同置换和替代过程。该方法使用最少轮数来确保算法的安全性。该算法可以支持并行计算。

Chen等人¹⁶提出了一种新方案，描述了一种基于格雷码的置换图像加密方案。这是一种基于混沌的密码系统。在该方案中，采用了一种新的置换策略来扩散像素

表1 术语表

Term	用法
μ	一个阈值，即 3.57≤μ ≤ 4
⌊⌋	向下取整函数
⊕	按位异或运算
dx	变量x的值的变化
dy	变量y的值的变化
W	图像的列
H	图像的行
X₀	混沌映射的初始值
Xᵢ	第i个混沌映射的值
Pᵢ	第i个像素的原始图像灰度值
Pᵢ′	第i个像素的原始图像修改后灰度值
Cᵢ	第i个像素的密文图像灰度值
H(S)	熵
L	像素总数
k	密钥
r	相关系数
Bᵢ	随机共享密钥

位置。该方案展示了从(n, k, p₁)格雷码到(n, k, p₂)格雷码之间的非线性变换，其中n的取值范围为 0≤n ≤2ᵏ−1，k为位数，p表示距离参数。不同的安全分析表明，该方案能够抵御各种攻击。

童等人²描述了该方案。为了实现高安全性的加密，他们设计了一种扰动高维混沌技术。使用Henon映射对图像进行扰动。此外，他们生成了一个独立的新的猫映射以实现置乱‐扩散过程。在此方案中，他们将图像划分为多个部分，且这些部分可以相互重叠。对于每个部分，使用独立的猫映射进行置乱。通过增加猫映射的控制参数来扩大密钥空间并提高安全性。利用独立的猫映射算法执行置乱过程，然后对该置乱图像应用扩散方法。

王a等人¹⁷提出了该方案。在此方案中，他们认为置换与扩散结构是两个不同的阶段。基于该结构，他们设计了这种快速图像加密算法。他们首先将图像划分为像素块，然后打乱块顺序并改变像素值。为了提高加密速度，他们应用了伪随机数。这些随机数由时空混沌映射生成。不同的理论分析和安全分析表明，该方案具有高安全性。

朱等人¹⁸提出了一种使用阿诺德猫映射和比特级置乱来加密图像的方案。在该方案中，他们描述了一种新的置乱过程，该过程在比特级上置乱像素位置，同时也改变像素值。该方案指出，每个像素根据比特位置被分为八个部分，然后通过比特级置乱对像素进行混淆。不同的安全分析表明，该方案具有很高的安全性。

3 背景

本节讨论了用于介绍我们提出的方案的预备知识。本文中使用的符号见表1。

3.1 朗顿蚂蚁细胞自动机

细胞自动机³²,³³,³⁴,³⁵,³⁶概念通过兰顿蚂蚁离散模型¹⁹实现，其中创建了一个由黑白格子组成的方形区域。利用这些细胞，我们实现了图灵机，它是一个二维矩阵，该二维矩阵具有一组简单的规则但表现出复杂随机行为。此处，该二维矩阵被视为带有黑白格子的棋盘。每块棋盘上仅有一只蚂蚁。

这里，蚂蚁在棋盘上开始执行，并遵循三条规则：
1. 当蚂蚁遇到黑色细胞时，向右旋转90°并移动到下一个细胞。
2. 当蚂蚁遇到白色细胞时，向左旋转90°并移动到下一个细胞。
3. 当蚂蚁离开细胞时，该细胞的颜色被反转。

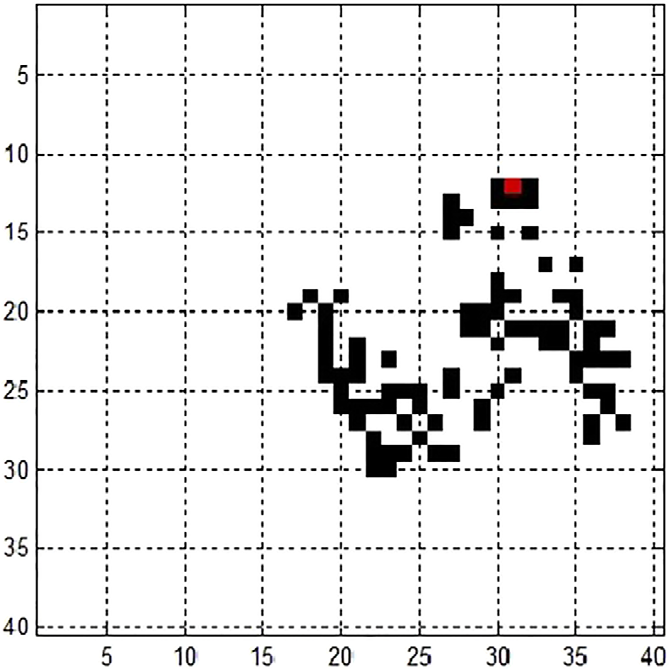
当蚂蚁从空单元格开始运行时，最终会构建一条“蚁道”（特定的类似道路的模式）。该蚁道由40步组成，重复一定有限次数的步骤，且蚂蚁在每一步移动中显示出水平、垂直单元格。图1展示了蚂蚁表现出的“随机行为”。

3.2 线性反馈移位寄存器

在计算中，线性函数线性反馈移位寄存器（LFSR）²⁰是一种依次移位其比特的寄存器，其输入位取决于先前状态。特定比特的线性函数通过异或（XOR）操作实现。因此，LFSR主要是一种移位寄存器，并通过异或（XOR）操作确定其输入位。

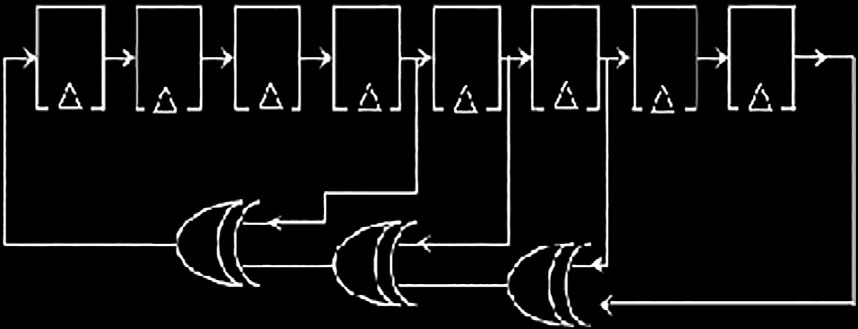
LFSR的初始值定义为种子，由于该寄存器的操作是确定性的，寄存器生成的值由其当前（或先前）状态决定。LFSR方程可以表示为模2多项式，其系数必须为0或1。因此，它也被称为反馈多项式或倒数特征多项式。图2显示了一个LFSR的示例。本文中，8阶LFSR被设计用于生成随机数。8阶LFSR的方程如下所示：

$$
P(x) = x^8 + x^6 + x^5 + x^4 + 1 \tag{1}
$$

3.3 混沌系统

混沌系统³的方程描述如下：

$$
X_{i+1} = (\mu + X_i^2) \cdot X_i \cdot (1 - X_i), \tag{2}
$$

其中 $3.57 \leq \mu \leq 4$ 和 $0 < X_i < 1$，且 $X_0 \in (0, 1)$ 被视为秘密边界值。该函数用于实现两个像素之间的扩散和混淆效应。

4 我们提出的方案

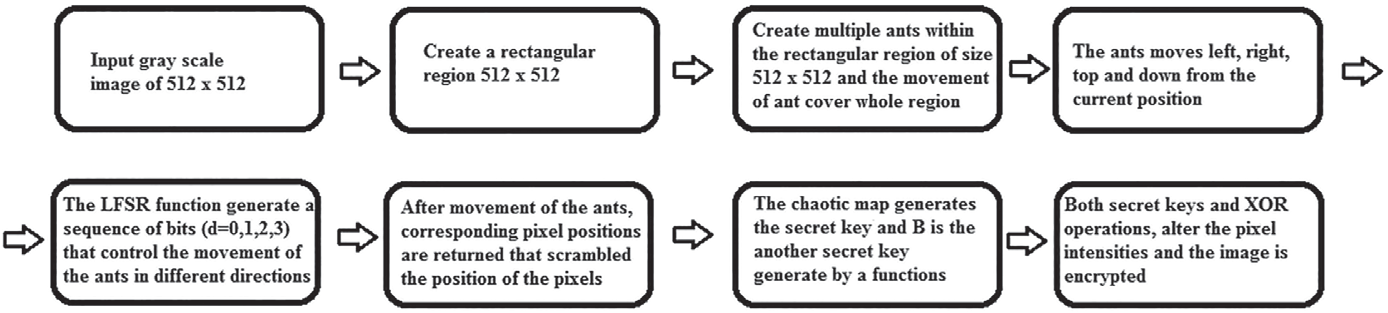
接下来，我们介绍我们的新方案，该方案使用多个蚂蚁细胞自动机来置乱像素位置，并结合混沌系统以改变所有像素的灰度值。为了在所提出的加密方案中实现混淆‐扩散：（a）我们在原始图像（灰度图像大小为512×512）中创建一个大小为512×512的矩形区域；（b）我们在该区域内部署多个蚂蚁，这些蚂蚁根据LFSR函数生成的移动模式同时移动，以实现像素位置的置乱；（c）利用混沌映射生成密钥；（d）对置乱后的像素与密钥进行按位异或操作，得到最终加密图像。图3展示了所提方案的框图。

4.1 加密算法

以下步骤描述了新的加密方案：
输入 ：大小为512×512的图像、密钥、X₀、μ、LFSR函数和混沌映射
输出 ：加密图像。

/* –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– Multiple Ant Cellular Automation –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– */

步骤1 ：创建多蚂蚁函数，步骤如下：
i) 通过512×512矩阵初始化缓冲区。
ii) 在矩阵中定义74只蚂蚁，每只蚂蚁完成47次迭代。
iii) 使用LFSR函数，每只蚂蚁从四个方向中选择一个方向移动，且不重复状态，方向可通过以下规则确定：
a) 如果 d = 0，蚂蚁在(x + 1, y)位置移动。
b) 如果 d = 1，蚂蚁在(x, y + 1)位置移动。 // 如下所述，即多蚂蚁细胞自动机
c) 如果 d = 2，蚂蚁在(x – 1, y)位置移动。
d) 如果 d = 3，蚂蚁在(x, y – 1)位置移动。
iv) 所有蚂蚁移动后，对应的坐标位置被存储到一个一维数组中。设Pᵢ(i = 1, · · ·, n)为得到的像素，其中n表示像素总数。

/* –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– 混沌映射 –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– */

步骤2 ：初始化参数X₀ = 0.0990099。
步骤3 ：计算 $X_{i+1} = (\mu + X_i^2) \cdot X_i \cdot (1 – X_i)$ 的值，其中 i = 1, 2, 3, · · ·, n，n为总像素数，3.57 < μ ≤ 4, 0 < Xᵢ < 1 且 X₀ = 0.0990099 ∈ (0, 1)。// 用于改变像素强度值（如下所述）。

/* –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– 像素强度值的改变 –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– –– */

步骤4 ：利用像素强度值改变技术，将Pᵢ转换为Cᵢ，其中 i = 1, · · ·, n。
步骤5 ：返回加密图像(Cᵢ, i = 1, · · ·, n)。

4.1.1 多蚂蚁细胞自动机

本文使用了一种基于LFSR的兰顿蚂蚁元胞自动机概念的变体，用于创建可并行运行的多个相似类型的蚂蚁²¹。由于可以并行运行，因此计算成本可能低于兰顿蚂蚁元胞自动机。此处，LFSR生成一个比特序列。我们计算d，其包含LFSR输出序列中的两个连续比特。d的十进制值可以是0、1、2或3。然而，d的值表示蚂蚁从当前位置出发的方向移动，即向左、向右、向上和向下。每只蚂蚁在一个由黑白格子组成的方格阵列上运行。

所有蚂蚁可以在一个矩形区域内运行。设一只蚂蚁的位置为(x, y)，蚂蚁在细胞上的移动遵循以下一组规则：根据上述四种情况之一，并且不重复相同位置的情况下，移动到一个新的位置。根据参考文献[37]，以扰乱所有像素的位置，我们在一个矩形区域内考虑74只蚂蚁，它们之间距离相等。对于每只蚂蚁，我们考虑47次迭代次数。图像的大小用于创建该矩形区域。所有蚂蚁都在矩形边界内移动。相对于每只蚂蚁的每次移动返回坐标位置。这些坐标位置实际上代表了图像的像素位置。

• 情况1 ：如果 d = 0，蚂蚁在(x + 1, y)位置移动
• 情况2 ：如果 d = 1，蚂蚁在(x, y + 1)位置移动
• 情况3 ：如果 d = 2，蚂蚁在(x − 1, y)位置移动
• 情况4 ：如果 d = 3，蚂蚁在(x, y − 1)位置移动

4.1.2 像素强度值的改变

我们可以使用以下两个步骤将像素值Pᵢ更改为Cᵢ：其中，n表示像素数量，Pᵢ表示第i个像素的灰度值，Pᵢ′表示第i个像素的修改后像素强度值，Xᵢ为从混沌系统中得到的值，被视为密钥，Bᵢ = ⌊Bᵢ₋₁ ⋅ 251⌋ mod 256。C₀和B₀的初始值被视为发送方和接收方之间共享的随机密钥，且它们的取值范围在1到255之间。

步骤1 ：
$$
P_i’ =
\begin{cases}
(P_i + 1) \cdot \lfloor k \cdot X_i \rfloor \mod 251, & \text{if } 0 \leq P_i < 251 \
P_i, & \text{otherwise}
\end{cases}
\tag{3}
$$
这里，我们考虑k = 2002。

步骤2 ：
$$
C_i =
\begin{cases}
P_i’ \oplus C_{i-1}, & \text{if } i = 1 \text{ and } C_0 \text{ is an initial random shared secret between sender and receiver} \
P_i’ \oplus C_{i-2} \oplus C_{i-1}, & \text{if } C_{i-1} \text{ is odd number and } i = 2, 3, 4, \cdots, n \
P_i’ \oplus B_i \oplus C_{i-2}, & \text{if } C_{i-1} \text{ is even number and } i = 2, 3, 4, \cdots, n
\end{cases}
\tag{4}
$$

5 统计分析

通常，参考文献22–24，本文从统计角度对所提出的方案（图像加密技术的安全性）进行了统计分析。一个好的加密算法应生成足够混乱的密文图像，使得攻击者难以从统计角度获取有用信息。我们基于一些统计分析方法对加密算法进行评估，如灰度图像的直方图、两个相邻像素的相关性和图像信息熵。实验采用Matlab 2010a（64位），实验设备配置为Microsoft Windows 7操作系统、Intel Core 2 Duo 2 GHz CPU、3GB内存。实验中选用多幅大小为512×512的图像，包括Lena、狒狒、芭芭拉和Peppers。

5.1 直方图分析

在图像处理中，灰度图像的直方图以图形方式描述了像素分布。¹⁸,²⁵实验结果表明，直方图的左侧对应具有大量像素的暗图像，而直方图的右侧对应非常亮的图像且包含少量暗区。此外，加密图像的直方图显示在图5中。

根据实验结果还可确定，密文图像与原始灰度图像的直方图完全不同。此处，密文图像显示其灰度值均匀分布。因此，无法通过频率分析来破解该方案。故而，该方案稳健地满足扩散性，且证明了任何企图均无法破解所提出的方案。

5.2 信息熵

1949年，香农首次提出了信息熵¹⁶,²⁶。它是信息源的重要数学特性之一，反映了图像的不确定性和随机性。以下方程描述了熵H(S)的

Lena，(a2)Lena的直方图，(a3)加密的Lena，(a4)加密Lena的直方图，(b1)狒狒，(b2)狒狒的直方图，(b3)加密的狒狒，(b4)加密狒狒的直方图，(c1)芭芭拉，(c2)Barbara的直方图，(c3)加密的Barbara，(b4)加密Barbara的直方图，(d1)peppers，(d2)peppers的直方图，(d3)加密的peppers (c4)加密peppers的直方图)

计算公式：

$$
H(S) = \sum_{i=0}^{2^L - 1} P(S_i) \log_2 \frac{1}{P(S_i)} \tag{5}
$$

其中，S为原始图像，L为对应于原始图像Sᵢ的像素总数，P(Sᵢ)为原始图像Sᵢ的概率。对于随机性，原始图像包含2ᴸ个符号。结果表明，密文图像的熵达到2⁸灰度值，接近理论值8。若密文图像的熵值为8，则可认为该图像加密方案能够抵御熵攻击。若灰度值偏离理想值，则说明密文图像未被充分随机化，存在一定程度的安全风险，从而威胁加密方案的安全性。

表2 使用我们提出的方案对不同密文图像进行的熵测试：一项分析

测试图像	原始图像	密文图像
Lena	7.4455	7.9993
狒狒	7.3579	7.9992
芭芭拉	7.4664	7.9993
Peppers	7.5715	7.9993

这表明我们提出的方案的可预测性较低。信息熵的以下结果表明，密文图像接近理论值8。因此，我们的方案能够抵御熵攻击。

5.3 敏感性分析

根据参考文献5,27,39，攻击者试图寻找线索以破解方案的安全性。因此，他/她可以通过对密钥或原始图像进行微小更改，从而在密文图像中产生变化。当原始图像发生微小变化时，密文图像应发生显著变化。

5.3.1 密钥敏感性

所提出的方案的解密算法通过以下步骤实现：

步骤1 ：
$$
P_i’ =
\begin{cases}
C_i \oplus C_{i-1}, & \text{if } i = 1 \
C_i \oplus C_{i-2} \oplus C_{i-1}, & \text{if } C_{i-1} \text{ is odd number and } i = 2, 3, 4,\dots, n \
C_i \oplus B_i \oplus C_{i-2}, & \text{if } C_{i-1} \text{ is even number and } i = 2, 3, 4,\dots, n
\end{cases}
\tag{6}
$$

步骤2 ：
$$
P_i =
\begin{cases}
P_i’ \cdot (\lfloor k \cdot X_i \rfloor)^{-1} - 1 \mod 251, & \text{if } 0 \leq P_i’ < 251 \
P_i’, & \text{otherwise}
\end{cases}
\tag{7}
$$

这里，k是另一个秘密信息且k = 2002。即使对秘密信息k和Xᵢ做出任何微小更改，攻击者也无法解密原始图像（见图6）。

5.3.2 明文图像敏感性

NPCR 和统一平均变化强度（UACI）是两个最受认可的参数，用于检验图像加密算法在面对差分攻击时的鲁棒性。通常，较高的 NPCR 和 UACI 值被认为具有较强的抵抗差分攻击的能力。²⁸当有意义的图像发生微小改变时，密文图像可能会产生显著变化，从而使攻击者无法提取出有意义（明文）图像与无意义（加密后）图像之间的关键信息。

接下来，我们使用公式来计算 NPCR 和 UACI¹⁶,²⁹,³⁰：

$$
\text{NPCR} = \frac{\sum_{i,j} D(i,j)}{W \cdot H} \cdot 100 \%, \tag{8}
$$

$$
\text{UACI} = \frac{\left| \sum_{i,j} |C_1(i,j) - C_2(i,j)| \right|}{L} \cdot \frac{100}{W \cdot H}, \tag{9}
$$

这里，C₁ 和 C₂ 分别表示原始图像中一个像素改变前后生成的两个加密图像，它们具有相同的尺寸 W ⋅ H（其中 W 为列数，H 为行数）。L 表示图像的最大灰度值。定义 D(i, j) = 1 当且仅当 C₁(i,j) ≠ C₂(i, j) 时成立，否则 D(i, j) = 0。加密后，实验图像显示大量像素已被改变。显然，后续像素之间的差异达到最大值，因此该方案对原始图像具有高度敏感性。

表3 使用所提出的方案对不同图像进行NPCR和UACI分析

	Lena	狒狒	芭芭拉	Peppers
NPCR	99.7524	99.7284	99.7395	99.7280
UACI	33.5723	33.4488	33.3989	33.4877

结果显示 NPCR 接近 100%，但 UACI 在 Lena、狒狒、芭芭拉和 Peppers 图像上有所差异。

5.4 两个相邻像素的相关性

明文图像的相关系数是统计分析中最重要的一项特征。它表明原始图像中相邻像素之间具有较强的相关性。但在密文图像中，如果像素之间的相关性越低，¹⁶,²⁹,³¹则加密技术的安全性越高。我们分别从Lena、狒狒、芭芭拉和 Peppers图像中计算X方向（水平）、Y方向（垂直）以及Z方向（对角线）的相关性，并利用以下方程确定每幅图像的相关系数：

$$
r = \frac{\sum d_x d_y}{\sqrt{\sum d_x^2 \sum d_y^2}} \tag{10}
$$

其中 $ d_x = (x - \bar{x}) $ 和 $ d_y = (y - \bar{y}) $ 以及 $ \bar{x} = \frac{\sum d_x}{n} $，$ \bar{y} = \frac{\sum d_y}{n} $ 和 $ n = W \cdot H $ 为像素数量。

表4 使用我们提出方案的两个相邻像素的相关性：一项分析

	水平	垂直	对角线
Lena
原始图像	0.9719	0.9850	0.9593
密文图像	0.00069	-0.00013	0.00041
狒狒
原始图像	0.8665	0.7586	0.7261
密文图像	-0.0012	-0.00065	0.0044
芭芭拉
原始图像	0.8597	0.9591	0.8418
密文图像	-0.0024	0.00049	0.0022
Peppers
原始图像	0.9792	0.9826	0.9680
密文图像	-0.0019	0.0028	-0.0012

由于明文图像Lena、狒狒、芭芭拉、Peppers对应的密文图像的相关系数接近于0，因此我们提出的算法能够抵御相关性攻击。

6 比较

所提出的方案与王和徐¹、陈等人¹⁶、童等人²、王a等人¹⁷以及朱等人¹⁸的方案进行了比较，我们使用相同的灰度数据集。特别是，这里我们将Lena原始图像作为标准图像，以与其他加密方案进行公平比较。计算了参考文献(1,2,16–18)中所有现有方案的加密图像的NPCR、UACI和信息熵。最终结果列于表5。

表5 相关方案与我们提出的方案对不同图像的NPCR、UACI和熵：比较

图像加密算法	NPCR	UACI	熵
我们的方案	99.7524	33.5723	7.9993
王和徐的方案¹	99.6307	33.5664	7.9993
陈等人的方案¹⁶	99.6132	33.4632	7.9992
童等人方案²	99.6922	33.3581	7.9999
王a等人提出的方案¹⁷	99.640	33.561	7.9994
朱等人 的方案¹⁸	99.6052	33.39	7.9993

7 结论

本文中，我们设计了一种新的加密方案，利用多个蚂蚁细胞自动机基于线性反馈移位寄存器（LFSR）和混沌系统来扰乱像素位置。我们修改了每个像素的灰度值。其主要思想是，多个蚂蚁可以在线性反馈移位寄存器（LFSR）生成的输出控制下，同时在一个矩形区域上移动，其中LFSR可被视为一种伪随机数序列。实验结果和各种统计分析表明，我们的方案表现良好。我们证明了我们提出的方案能够有效抵御常见的已知统计攻击。本文显示，NPCR、UACI和信息熵均取得了较好的结果。此外，所提出的方案具有安全性和实用性。