无安全信道多关键词搜索加密

不可区分陷门的无安全信道多关键词搜索公钥加密（学生贡献）

1 引言

计算机在过去的几十年中对社会文明和进步起到了至关重要的作用。近年来，计算机在连接人们以及为社会和企业创造巨大效益方面变得越来越普遍。随着互联网的发展，企业和个人更愿意将数据存储到第三方（即云服务器）中，以节省本地内存、降低成本并实现额外备份。然而，将数据保存在第三方可能会带来一些负面影响。存储的数据可能开始承受各种攻击的冲击。

例如，黑客热衷于进行端口扫描，以利用系统的漏洞主机，然后在无需认证的情况下侵入受害者的系统，最终常常破坏操作系统。此外，一些不友好的黑客可能会捕获网络上的数据包，然后尝试解包这些数据包以获取信息。黑客攻击在金钱和精力上都带来了巨大损失。因此，许多专家和技术人员致力于在一定程度上避免这些攻击。值得注意的是，带关键词搜索的公钥加密（PEKS）是确保数据传输安全性的最先进的密码系统之一。

Boneh 等人[4]于2004年提出了第一个基于关键词搜索的公钥加密（PEKS）方案，该方案允许用户通过特定关键词搜索加密消息，而不会危及原始数据的安全性。该方案在选择明文攻击下具有不可区分性（IND‐CPA），但存在一些局限性。例如，它要求服务器与接收者之间建立安全信道，但在某些情况下构建安全信道成本高昂且不现实。因此，Baek 等人[1]提出了一种新方法，从原始PEKS方案中移除安全信道，即“无安全信道的公钥加密关键词搜索（SCF‐PEKS）”。实际上，用于搜索的关键词是有限的，可能遭受关键词猜测攻击（KGA）。Byun 等人[5]首次发现 PEKS容易受到离线KGA的威胁。Tang 等人[12]提出了一种新的抵抗离线KGA的PEKS方案，但其加密算法较为复杂。随后， Rhee 等人[11]指出KGA可能破坏SCF‐PEKS方案，因此他们设计了一种满足陷门不可区分性特性的新型SCF‐PEKS方案，以防止 KGA。2013年，Zhao 等人[15]提出了一种高效的具有陷门不可区分性的SCF‐PEKS方案，性能优于Rhee等人的方案。上述 PEKS机制仅支持“精确”关键词搜索，无法处理拼写不一致（如 “common”和“comon”）或格式差异（如“PhD”和“ Ph.D”）等情况。因此，Li 等人[10]首次将“模糊关键词搜索”概念引入加密模型以解决这些问题。2013年，Xu 等人[14]提出了一种支持模糊关键词搜索的新PEKS方案，可抵抗离线KGA。近年来还提出了其他典型的PEKS方案。Ibraimi 等人[9]提出了支持委托搜索的PEKS，用于检测加密的恶意代码。Chen 等人[6]于2016年形式化了双服务器PEKS，以抵御固有的不安全性。同时，He 等人[8]提出了一种新的PEKS方案，使用户能够在移动社交网络中共享内容并订阅服务。然而，上述PEKS方案均专注于单个关键词的加密，而非多个关键词。Baek 等人[1]提出了一种 PEKS方案以解决多关键词搜索问题，但它需要通过安全信道传输陷门。2016年，Wang 等人[13]正式定义了“无安全信道的多关键词公钥加密搜索（SCF‐MPEKS）”，以消除对安全信道的需求。然而，SCF‐MPEKS可能如果恶意服务器或接收者将其私钥泄露给公众，则可能遭受关键词猜测攻击（KGA）。

本文形式化定义了不可区分陷门的无安全信道多关键词搜索公钥加密（tSCF-MPEKS）模型，随后提出了 tSCF‐MPEKS的一种构造方法，并在BDH和1‐BDHI假设下证明了其安全性。该提出的方案具有密文不可区分性和陷门不可区分性，能够抵抗关键词猜测攻击和选择明文攻击。

2 方法论

2.1 双线性对

设G1和GT为两个循环群（G1表示一个加法群，GT表示一个乘法群）。д是G1的生成元，大素数p是G1的阶。令x和y为Zp中的元素。双线性对可以看作是一个映射e: G1 ×G1 → GT，具有以下性质：

i. 双线性：e(xM, yN) = e(M, N)xy对于所有 M, N ∈ G1 且 x, y ∈Zp。

ii. 可计算性：e(M, N) ∈ GT可通过多项式时间算法计算，对于任意 M, N ∈ G1。

iii. 非退化性：e(M, N) , 1。

2.2 双线性Diffie‐Hellman假设[3]

给定输入P, xP, yP, zP（其中x, y, z ∈Zp），计算e(P, P)xyz ∈GT。若算法A在G1中求解BDH假设的成功概率为Pr[A(P, xP, yP, zP) = e(P, P)xyz ] ≥ ε，则称算法A在求解G1中的BDH假设上具有优势 ε。如果不存在t时间算法在求解G1中的BDH假设时具有至少 ε的优势， 则认为BDH假设在G1中成立。

2.3 1‐双线性Diffie‐Hellman逆（1‐BDHI）假设[2]

给定输入P、xP（其中x ∈Zp），计算e(P, P) 1 x。若算法A在G1中求解1‐BDHI假设的优势为Pr[A(P,xP) = e(P, P) 1 x] ≥ ε，则称该算法具有此优势。如果不存在运行时间为t且求解G1中1‐BDHI假设的优势至少为 ε的算法，则认为1‐BDHI假设在G1中成立。

3 陷门不可区分的安全信道无关公钥加密与多关键词搜索

3.1 tSCF‐MPEKS的通用模型

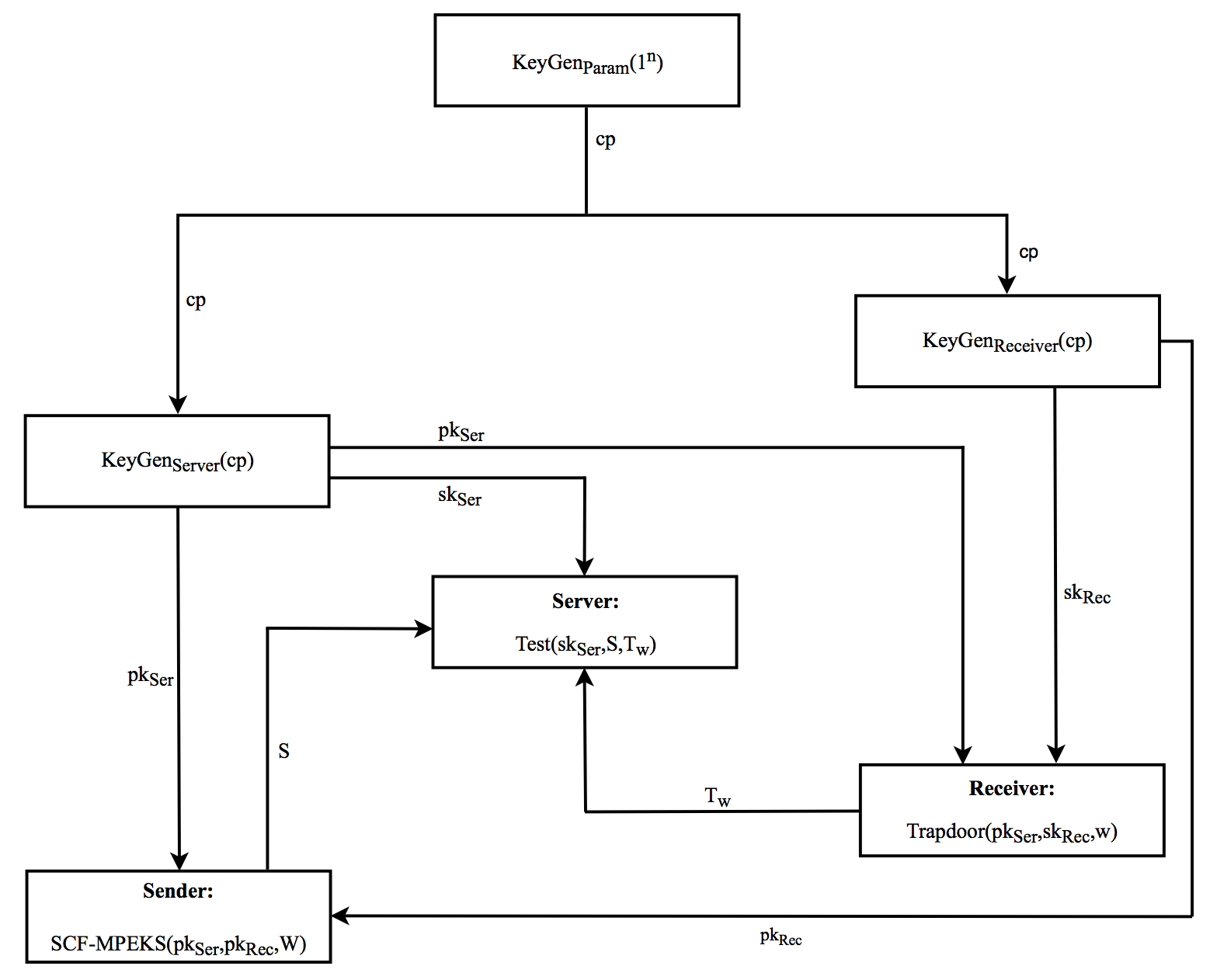
在tSCF‐MPEKS模型中，发送方、服务器和接收者是三个参与方。具体而言，发送方是创建SCF‐MPEKS加密的一方，而接收者是生成陷门查询的一方。发送方和接收者都将各自的加密消息传输给服务器。然后，服务器运行测试算法来检查两条加密消息是否包含相同的关键词。具体细节如下所述：

1. KeyGenParam(1n)：输入1n，然后生成一个公共参数cp。

2. KeyGenServer(cp)：输入cp，然后生成服务器的公钥和私钥对（ pkSer， skSer）。

3. KeyGenReceiver(cp)：输入cp，然后生成接收者的公钥和私钥对 (pkRec, skRec)。

4. SCF −MPEKS(pkSer,pkRec,W)：输入服务器的公钥pkSer和接收者的公钥pkRec，然后生成关键词向量W=(w1, w2, …,wn)的可搜索加密S。

5. Trapdoor(pkSer, skRec,w)：输入服务器的公钥pkSer和接收者的私钥skRec，然后生成关键词w的陷门Tw。

6. Test(skSer, S,Tw)：输入服务器的私钥skSer、一个可搜索加密S= SCF −MPEKS(pkSer,pkRec,W)以及一个陷门Tw=Trapdoor(pkSer, skRec, w)。如果W包含w，则输出“yes”；否则，输出“no”。

3.2 tSCF‐MPEKS的安全模型

如[1, 13],中所述，tSCF‐MPEKS 是 IND‐CPA 和 陷门‐IND‐CPA 的。

IND‐CPA安全性是指，如果恶意服务器未收到包含给定关键词的陷门，则其无法判断哪个SCF‐MPEKS密文包含哪个加密关键词。此外，如果恶意接收者未获得服务器的私钥，则即使其截获了任意关键词的所有陷门，也无法验证 SCF‐MPEKS密文与陷门是否具有相同的关键词。

陷门‐IND‐CPA安全性是指一个不包括服务器和接收者的外部攻击者无法区分两个挑战关键词的陷门之间的任何差异。

tSCF‐MPEKS的IND‐CPA和陷门选择明文攻击下的不可区分性形式化定义如下：设A为运行时间受限于t的攻击者，E为挑战者。

游戏1 ： A被假定为一个恶意服务器。

设置 ： 挑战者 E 首先运行 KeyGenParam(1n)、KeyGe−nServer (cp) 和 KeyGenReceiver(cp)，以生成公共参数 cp、服务器的公私钥对（pkSer, skSer）以及接收者的公私钥对（pkRec, skRec）。然后，攻击者 A 接收 cp、pkSer、skSer 和 pkRec。

阶段1‐1（陷门查询） ：攻击者 A 可以请求 E针对任意关键词 w 的陷门Tw。

挑战 ：A 向 E 发送一个目标关键词向量对 (W0, W1)，希望 E 对其进行挑战，其中 W0=(w01, ...., w0n) 和 W1=(w11, ...., w1n)。注意，W0 和 W1 不能在阶段1‐1中被查询。一旦 E 收到该目标关键词向量对，他/她将运行 SCF −MPEKS 算法生成一个可搜索加密 S=SCF −MPEKS(pkSer , pkRec,Wλ)，其中 λ ∈{0, 1}。最后，E 将 S 发送给 A。

阶段1‐2（陷门查询） ：A 可以继续向 E 请求任意关键词 w的陷门 Tw，与 阶段1-1 中相同，但需满足 w, w0,w1。

猜测 ：攻击者 A 输出猜测 λ∗ ∈{0, 1} 并在 λ∗= λ 时赢得 游戏1。

游戏2 ： A被假定为一个恶意接收者。

设置 ： 挑战者 E首先运行 KeyGenParam(1n)、KeyGe−nServer (cp) 和KeyGenReceiver(cp)，以生成一个公共参数 cp、服务器的公私钥对 (pkSer, skSer) 以及接收者的公私钥对 (pkRec, skRec)。然后，攻击者 A接收 cp、pkRec、skRec和 pkSer。

挑战 ：A 发送一个目标关键词向量对 (W0, W1)，希望 E对其发起挑战，其中 W0=(w01, ...., w0n) 且 W1=(w11, ...., w1n)。注意，在测试算法中不能查询 Tw0i 和 Tw1i，其中 i = 1, …, n。一旦 E 收到目标关键词向量对，他/她将运行 SCF −MPEKS 算法以生成可搜索加密 S=SCF−MPEKS(pkSer , pkRec,Wλ) , 其中 λ ∈{0, 1}。最后，E将S发送回A。

猜测 ：A 输出猜测 λ∗ ∈{0, 1} 并赢得 游戏2，如果 λ∗= λ。

A赢得游戏1 和游戏2 的优势如下：
AdvIN D−CPA tSCF −MPEKS,Ai( k)= |Pr[λ∗= λ] − 1/2|.(i= 1, 2)

因此，只有当AdvIND−CPAtSCF −MPEKS,Ai(k) 可忽略时， tSCF‐MPEKS 模型才可被视为 IND‐CPA 安全。

Game3 : A被假定为排除服务器和接收者之外的外部攻击者。

设置 ：挑战者E首先运行KeyGenParam(1n)、KeyGe− nServer (cp) 和 KeyGenReceiver (cp)，以生成公共参数cp、 服务器的公私钥对(pkSer, skSer)以及接收者的公私钥对 (pkRec, skRec)。然后，攻击者A获得cp、pkRec和pkSer，而 skRec与skSer不会发送给A。

阶段3‐1（陷门查询） ：攻击者A可以自适应地向E请求任意关键词 w的陷门Tw。

挑战 ：A 发送一个目标关键词对(w0, w1)，希望由E对其进行挑战。显然，w0和w1均未在阶段3-1中被查询过。一旦E收到目标关键词对，他/她将运行Trapdoor算法生成一个陷门Tw= Trapdoor(pkSer, skRec,wλ)，其中 λ ∈{0, 1}。最后，E将Tw发送回 A。

阶段3‐2（陷门查询） ：A 可以继续向E请求任意关键词w的 陷门Tw，如同在阶段3-1中一样，只要w, w0,w1。

猜测 ：A 输出猜测 λ ∗ ∈{0, 1} 并赢得 Game3，如果 λ ∗ = λ。

A赢得 Game3的优势如下：
AdvTrap −IN D−CPA tSCF −MPEKS,A3(k)= |Pr[λ∗= λ] − 1/2|.

因此，仅当AdvTrap −IND−CPA tSCF −MPEKS,A3(k)可忽略时， tSCF‐MPEKS模型才可被视为是陷门‐IND‐CPA安全的。

4 提出的tSCF‐MPEKS方案

4.1 tSCF‐MPEKS的构造

1. KeyGenParam(k) ：假设G1是一个加法循环群，GT是一个乘法循环群。д是G1的一个随机生成元，其阶为素数p ≥ 2k。双线性对是一个映射e : G1 ×G1 →GT。设H : {0, 1}◦ → G1 和 H∗: GT →{0, 1}•为两个特定的哈希函数。该算法返回公共参数cp ={д, p, G1, GT, e, H, H∗}。

2. KeyGenServer(cp) ：服务器从Zp中均匀随机选择一个元素a，并计算A = aP。此外，服务器还从G1中均匀随机选择B。因此，服务器的公钥为 pk _Ser = (cp, A, B)，私钥为sk _Ser = (cp, a)。

3. KeyGenReceiver(cp) ：接收者随机选择 c ∈Zp，然后计算 C= cP。因此，接收者的公钥为 pkRec=(cp,C)，私钥为 skRec=(cp, c)。

4. SCF −MPEKS(pkSer , pkRec,W ) ：发送方随机选择 t ∈Zp，然后计算可搜索加密 S =(M, N1, N2, .. ., Nn)=(tA, H∗(D1), H∗(D2), …, H∗(Dn))，其中 D1=e(H(w1), C)t ， D2=e(H(w2), C)t ,…, Dn =e(H(wn),C)t 。

5. Trapdoor(pkSer, skRec,w∗) ：接收者随机选择 t∗ ∈Zp，然后计算Tw=(T1,T2)，其中T1= cH(w∗)⊕e(A, B)t∗+c和 T2= e(A,t∗B)。

6. 测试(S,Tw, skSer) ：对于 i ∈{1, 2, …, n}，服务器 首先计算 T = T1 ⊕ T2 • e(aB,C) = cH(w ∗ )。然后，服务器 检查是否 H ∗ [e(T, Ma )]=Ni。如果是，输出“yes”；否则，输出“no”。

4.2 tSCF‐MPEKS的正确性

假设W是SCF −MPEKS方案中的一个关键词向量，w∗分别是陷门算法中的一个关键词。如果W包含w∗，则该方案是正确的。具体细节如下：对于i ∈{1, 2, …,n}，

首先，
T= T1 ⊕ T2 • e(aB, C)
= cH(w ∗ ) ⊕ e(A, B) t∗+c ⊕ e(A, t ∗ B) • e(aB, cP)
= cH(w ∗ ) ⊕ e(A, B) t∗+c ⊕ e(A, B) t∗ • e(A, B) c
= cH(w ∗ ) ⊕ e(A, B) t∗+c ⊕ e(A, B) t∗+c
= cH(w ∗ )

然后，
H ∗ [e(T, M a )]= H ∗ [e(cH(w ∗ ), tA a )] = H ∗ [e(cH(w ∗ ), tP)] = H ∗ [e(H(w ∗ ), C) t ] = Ni

4.3 tSCF‐MPEKS的安全性分析

定理4.1. 上述tSCF-MPEKS方案在随机预言模型下假设双线性 Diffie-Hellman假设难以成立时，在游戏1 中针对选择明文攻击是 IND-CPA安全的。

游戏1：A 被假定为一个恶意服务器。

证明。 假设 以<д>、

、 <1>、 、 、 、

、 作为双线性Diffie‐Hellman假设的输入，其运行时间受限于 。 的目标是利用 的IND‐CPA，计算出关于 、

和 的BDH密钥 (

,

) 。此外，假设

最多提出 次和 ∗哈希函数查询。

设置模拟
E首先设置C= xP，并均匀随机地选择a ∈ Zp，然后计算A= aP。E还从B ∈ G1中均匀随机选取。最后，E返回（д,p, G1, GT, e, H, H ∗）作为公共参数cp，（cp,A,B）作为服务器的公钥/私钥， 以及（cp,C）作为接收者的公钥。此外，E选择两个哈希函数H和 H ∗如下：

• A可以随时对关键词wi向 H函数发起查询。作为响应，E在 H_List 中搜索一个元组 (wi, Fi, f i, θ i)，而初始时 H_List为空。如果该元组存在，A将收到 H(wi) =Fi作为响应。否则，E执行以下步骤：
  i. E均匀随机选取一枚硬币 θ i，然后计算Pr[θ i= 0]= 1 h+1。
  ii. E均匀随机选择 f i ∈Zp。如果 θ i= 0，E将计算Fi= yP+f iP。如果 θ i = 1，E将计算Fi=f iP。
  iii. E返回Fi作为对A的响应，并将(wi, Fi, f i, θ i)添加到H列表中。_

• A可以随时向 Di查询 H ∗函数。然后，E在 H ∗ _List中搜索元组 (Di, Ni)。如果该样本存在，A将收到 Ni作为响应。否则，E均匀随机地选择 Ni ∈ {0, 1}d，然后将其返回给 A，并同时将 (Di, Ni) 添加到 H ∗ _List中。

阶段1‐1模拟（陷门查询）
当A针对词语wi对应的陷门发起查询时，E执行以下步骤进行响应：
- E运行上述用于模拟H函数的算法，以创建一个元组（wi，Fi，f i，θ i）。如果 θ i= 0，E将停止并输出“Suspension”。否则，E执行下一步。
- E 选择 t ∗ ∈ Zp，然后计算 T1 = fiC ⊕ e(A, B)t ∗ +x =fixP ⊕e(A, B)t ∗ +x =xFi ⊕e(A, B)t ∗ +x =xH(wi ) ⊕e(A, B)t ∗ +x 以及 T2 =e(A, t ∗ B)。因此，关键词w的陷门 Tw =(T1,T2)。

挑战模拟
A发送W0 =(w01,w02, … 向量对后，E按如下方式响应：
- E随机选择 i ∈{1, 2, …,n}。
- E运行上述算法以模拟H函数，得到两个元组（w ∗ 0i，F ∗ 0 i，f ∗ 0 i， θ ∗ 0i）和（w ∗ 1i，F ∗ 1 i，f ∗ 1 i， θ ∗ 1i）。如果 θ ∗ 0i和 θ ∗ 1i均等于1，则E将停止并输出“Suspension”。否则，E执行下一步。
i. E 运行上述模拟 H 函数的算法共 2(n −1) 次，以获得两个元组向量 ((w ∗ 01 , F ∗ 01 , f ∗ 01 ,θ ∗ 01 ), …, (w ∗ 0i−1, F ∗ 0i−1, f ∗ 0 i−1, θ ∗ 0i−1), (w ∗ 0i+ 1, F ∗ 0i + 1, f ∗ 0 i + 1, θ ∗ 0i+ 1), …, (w ∗ 0n, F ∗ 0n, f ∗ 0n, θ ∗ 0n)) 和 ((w ∗ 11 , F∗ 11 , f ∗ 11 ,θ ∗ 11 ), …, (w ∗ 1i−1, F ∗ 1 i −1 , f ∗ 1 i −1 ,θ ∗ 1 i −1) , (w ∗ 1 i + 1 , F ∗ 1 i + 1 , f ∗ 1 i + 1 ,θ ∗ 1 i + 1) , …, (w ∗ 1 n, F ∗ 1 n, f ∗ 1 n, θ ∗ 1 n))。如果 θ ∗ 0j 和 θ ∗ 1j 相等 对于所有j= 0，…，i − 1，i+ 1，…，n，若不成立，则E将停止并输出“Sus‐pension”。否则，E按如下方式响应：
– E随机选择 β ∈{0, 1}d。
– E随机选择 Jj ∈{0, 1} d并创建一个目标 SCF−MPEKS 密文 S∗=(M ∗, N ∗ 1, N ∗ 2, …, N ∗n) =(zA, J1, J2, …, J n)) 因此，S∗=(M∗, N ∗ 1, …, N ∗i−1, N ∗i+1, …, N ∗n) =(zA, H ∗[e(H(wβ1), C)z],.. .,H ∗[e(H(wβi−1), C)z],H ∗[e(H(wβi+1), C)z],…,H ∗[e(H(wβn), C)z]) 注意 Jj = e(H(wβ i),C)z = e(yP+fβ iP, xP)z = e(yP, xP)z • e(f β iP, xP)z = e(P, P)xyz • e(zP, xP)f β i 注意，e(fβkP, xP)z= e(fβkP,C)z= e(H(wβk), C)z

阶段1‐2模拟（陷门查询）
A可以继续向E发起关于关键词wi的陷门查询。E按照阶段1-1的方式 回答A，只要wi< W0,W1。

猜测
A输出猜测 β ∗ ∈{0,1}。然后，E从列表中选择 d作为H ∗函数，并返回d β ∗ i e(zP,xP) fβ ∗ i作为BDH密钥的猜测。

游戏1的分析
定义了三个事件如下：事件1：E在阶段1‐1和阶段1‐2（陷门查询）期间未中止。事件2：E在挑战模拟期间未中止。事件3： A未对H ∗(e(H(w ∗ 0i), C)z) 或 H ∗(e(H(w ∗ 1i), C)z) 发起查询。

声明1 ：Pr[Event1] ≥ 1e
证明 . 假设A在陷门查询中不会两次发布相同的关键词。因此， 一次陷门查询导致E暂停的概率为 1h+1。因此，由于A最多提出h次陷门查询，E在所有查询中均不暂停的概率至少为(1 − 1h+1)h≥ 1 e。

声明2 : Pr[Event2] ≥(1h+1) •( hh+1) 2 (n−1)
证明 。如果 θ0= θ1= 1，E将在挑战模拟期间暂停。因此，E不暂停的概率为 1−(1− 1h+1)2。此外，如果对于所有j= 0，…， i−1，i+1，…，n，θ ∗ 0j和 θ ∗ 1j均等于0，则E在此处也会暂停。因此，E在挑战模拟期间不暂停的概率至少为(1 − 1h+1) 2(n−1) {1 −(1 − 1h+1) 2 } ≥( 1h+1) •( hh+1) 2(n−1)。

声明3 ：Pr[Event3] ≥ 2ε
证明 . 如.[1],中所述，假设对于r ∈{1, 2, …,n}，混合事件r是指攻击者A能够成功猜测由wβ的前r个坐标和w1−β的后(n −r)个坐标构成的“混合” SCF −MPEKS密文左侧部分关键词的事件。因此，Pr[事件3]= 2Σnk = 1 = 2 = 2ε (Pr[混合事件r ]−Pr[混合事件r −1]) (Pr[混合事件r ] −Pr[混合0])。由于A对H∗ (e(H(w ∗ 0i ), C)z)或H ∗ (e(H(w ∗ 1i ), C)z)发起查询的概率至少为 2ε，因此A对H∗ (e(H(w ∗ ji ), C)z)发起查询的概率至少为 ε。总体而言，E的成功概率 ε ∗为(hh+1) 2 (n−1)• ε e(h+ 1)h ∗。

定理4.2 。 上述tSCF-MPEKS方案在随机预言模型下假设1-BDHI问题是难解的，则在游戏2中对选择明文攻击是IND-CPA安全的。

游戏2：A 应该是一个恶意接收者。

证明 。假设E的输入为1‐BDHI假设下的(д, p,G1,GT, e, xP)，其 运行时间受限于T。E的目标是利用A的IND‐CPA能力计算出 关于xP的1‐BDHI密钥e(P,P) 1 x。此外，假设A最多提出h和h∗ 次哈希函数查询。

设置模拟
E首先设置A= xP和B ∈ G1。E还均匀随机地选择c ∈Zp，并计算C= cP。然后，E返回（д, p, G1,GT, e, H, H ∗）作为公共参数 cp，（cp,A,B）作为服务器的公钥，（cp,C）和（cp,c）作为接收者的公钥/私钥。此外，E选择两个哈希函数H和H ∗如下：
– A可以随时向H 函数查询一个关键词wi 。为了响应，E均匀随机地 选择f i ∈ Zp，然后计算Fi= f iP，最后将Fi作为响应返回给A。
– A可以随时向 Di发起 H ∗函数的 查询。然后，E在 H ∗_List中搜索元组 (Di, Ni)。如果该样本存在，A将收到 Ni作为回应；否则，E均匀随机地 选择 Ni ∈{0, 1}d，将其返回给 A，并将元组 (Di, Ni) 添加到 H ∗_List中。

挑战模拟
A 向 E 发送 (W 0 ∗ i, F 0∗i, f 0 ∗ i, θ ∗ 0i ) 和 (W 1 ∗ i, F∗ 1i, f 1 ∗ i, θ ∗ 1i )，其中 W ∗ 0 =(w01, w02, …, w0n) 且 W ∗ 1 =(w11, w12, …, w1n)。E 随机选择 Jj ∈{0, 1}d 和 β ∈{0, 1}d。然后，E 构造一个目标无安全信道 MPEKS 密文 S∗=(M∗, N 1∗ , N 2∗ , …, N ∗n) =(ψxP, J1, J2, …, Jn)。 因此，S∗ =(M∗, N 1∗ , N 2∗ , …, N ∗n) =(ψxP, H∗(e(H(wβ 1), C)ψ), H∗(e(H(wβ 2), C)ψ), …, H∗(e(H(wβ n), C)ψ))。注意 e(H(wβ ∗ i), C)ψ) = e(fiP, cP)ψ=e(P, P)ψ·f i c。

猜测
A输出猜测 β ∗ ∈{0, 1}。然后，E从列表中选择 d作为 H ∗函 数的值，并返回 ψ= 1x·f ic作为对1‐BDHI密钥的猜测。

游戏2的分析
定义了两个事件如下：Event4：E在挑战模拟过程中未被终止。Event5：A未对 H ∗(e(H(w ∗ 0i),C)ψ) 或 H ∗(e(H(w ∗ 1i), C)ψ) 发起关键词w的陷门查询。

声明4 ：Pr[Event4]= 1
Proof . There i没有限制 i 为了表明E在挑战模拟期间将被暂停。因此，很容易知道Pr [ 4]= 1

声明5 ：Pr[¬Event5] ≥ 2ε
Proof . When Event5 h 发生时，已知表示密文是否包含w0i或w1i的比特j ∈{0, 1}与A的视图无关。因此，A输出的j ∗满足j=j ∗的概率至多为 12。根据贝叶斯法则，Pr[j=j ∗ ]=Pr[j=j ∗ |Event5]Pr[Event5]+Pr[j=j ∗ |Event5]Pr[¬Event5] ≤ Pr[j=j ∗ |Event5]Pr[Even5]+Pr[¬Event5]= 1 2 •Pr[Event5]+Pr[¬Event5]= 1 2 + 1 2 •Pr[¬Event5]
根据定义，显然有 |Pr[j= j ∗] − 1 2| ≥ ε。然后， ε ≤ Pr[j= j ∗] − 1 2 ≤ 1 2 • Pr[¬Event5]。因此，Pr[¬Event5] ≥ 2ε。
因为A对H∗(e(H(w∗ 0i ), C)ψ)或H∗(e(H(w∗ 1i ), C)ψ)发起查询的概率至少为 2ε，所以A对H∗(e(H(w ∗ji ), C)ψ)发起查询的概率 至少为 ε。由于A最多提出h∗次哈希函数查询，因此E选择正确答案的概率至少为 1h∗。总体而言，E的成功概率 ε ∗为 εh∗。

定理4.3 . 上述tSCF-MPEKS方案在随机预言模型下假设BDH 假设难解时，在Game3中针对CPA是陷门-IND-CPA安全的。

Game3: A应为一个不包括服务器和接收者的外部攻击者。

证明 。假设E以д、p、G1、GT、e、xP、yP、zP作为BDH假设 的输入，其运行时间受限于T。E的目标是利用A的I ND‐CPA来计算xP、yP和zP的BDH密钥e(P,P)xyz。此外，假 设A最多提出h和h∗次哈希函数查询。

设置模拟
E首先设置A= xP、B= yP和C= zP，然后返回(cp, A, B)作为服务器的公 钥，以及(cp,C)作为接收者的公钥。E还随机选择两个H和H ∗哈希函数。

阶段3‐1 模拟（陷门查询）
当A发起关于关键词wi的陷门查询时。为了响应，E均匀随机地选择t∗ ∈Zp，然后计算T1= zH(wi) ⊕ e(yP, xP)t∗+z和T2= e(t∗yP, xP)。因此，Tw=(T1,T2)。最后，E将Tw返回给A。

挑战模拟
A发送 (w∗ 0 ,w∗ 1) 给 E . E 如下构造挑战陷门：E 随机选择一个比特 β ∈{0,1}d。 因此，T1= zH(wβ ∗ ) ⊕e(yP, xP)t ∗ +z = zH(wβ ∗ )⊕e(P, P)xyz•e(P, P)xyt ∗且T2= e(t ∗yP, xP)。

阶段3‐2 陷门查询模拟
A可以继续向E发起关于关键词wi的陷门查询。E按照阶段3-1的方式 回答A，只要wi, w0,w1。

猜测
A输出猜测 β ∗ ∈{0, 1}。如果 β= β ∗，E输出“是”。否则， E输出“否”。

对Game3的分析
由于A是一个恶意的外部攻击者，即使两个陷门具有相同的关键词，他/她也无法区分这两个陷门之间的任何差异。原因是E随机选择t ∗ ∈ Zp，并且t ∗每次都会变化，导致T 1 = cH(wi) ⊕ e(A, B)t∗+c每次也不同。即使两个陷门具有相同的关键词，由于t ∗的存在，结果仍然不同。因此，tSCF‐MPEKS中 陷门不可区分性的关键部分在于保护e(A, B)t∗+c的机密性。假设攻击者A获得了e(A, B)t∗ + c的值，他/她就能区分两个陷门是否 具有相同的关键词。原因是攻击者A仅额外计算了一次异或操作，即T1=cH(wi ) ⊕e(A, B)t ∗+c ⊕e(A, B)t ∗+c =cH(wi )。因此，只要w0= w1，攻击者A就能区分Tw0= cH(w0)和Tw1= cH(w1)是否 相等。根据Game3中的挑战模拟可知，e(A, B)t ∗+c = e(P, P)xyz • e(P, P)xyt ∗，这满足BDH假设。因此，攻击者A无法 计算出e(A, B)t ∗+c的值，也就无法计算出T1=cH(wi ) ⊕ e(A, B)t ∗+c。

5 比较与性能

本节对提出的方案（tSCF‐MPEKS）与另外两种典型方案 （MPEKS[1]和SCF‐MPEKS[13]）之间的安全性进行了比较。此外，本部分还描述了提出方案的性能。

方案	密文不可区分性	陷门不可区分性	SC	KGA
MPEKS	满足	不满足	需要	易受KGA攻击
SCF‐MPEKS	满足	不满足	不需要	易受KGA攻击
提出的方案	满足	满足	不需要	不易受KGA攻击

CT Ind、Trap Ind、SC 和 KGA 分别是密文不可区分性、陷门不可区分性、安全信道和关键词猜测攻击的缩写。

使用JPBC库中的A类配对对提出的方案进行模拟[7]。模拟平台的条件如表2所示，时间开销如表3所示。然而，提出的方案移除了安全信道，使得陷门可以通过公共网络传输。此外，提出的方案满足密文不可区分性和陷门不可区分性，能够抵抗 KGA。总体而言，提出的方案性能优于Baek等人提出的 MPEKS[1]和王等人提出的SCF‐MPEKS[13]方案。

表2：模拟平台
OS	macOS Sierra 10.12.5
CPU	2.5 GHz Intel Core i7
内存	16 GB 1600 MHz DDR3
硬盘	512GB
编程语言	JAVA

表3：通过1000次计算机仿真得到的性能（n=3）
tSCF‐MPEKS	平均时间
密钥生成_服务端	0.017秒
密钥生成_接收方	0.012秒
SCF‐MPEKS	0.088秒
陷门	0.045秒
Test	0.019秒

6 结论

本文重新研究了MPEKS和SCF‐MPEKS方案，然后定义了不可区分陷门的无安全信道多关键词搜索公钥加密（tSCF-MPEKS）模型，并提出了一个具体的方案。该提出的方案解决了多关键词搜索问题，并具备无需安全信道的优点，使其成为一个实用且节省成本的系统。与tSCF‐MPEKS方案和其他方案的安全性相比，满足陷门不可区分性的提出方案更加安全，能够防止KGA。此外，通过1000次计算机仿真表明，该提出方案效率高，性能优异。