凸函数定义判定和性质简介

凸集

给定集合$S$，对任意元素$x_1$,$x_2$属于该集合$S$,若对于任意$\vartheta \in [0,1]$,有$$x=\vartheta x_1+(1-\vartheta )x_2$$,$x$也在集合$S$中，则集合$S$是凸集。
以向量的角度来理解，就是点$x_1$、$x_2$在集合$S$中，两点的连线也在该集合中。

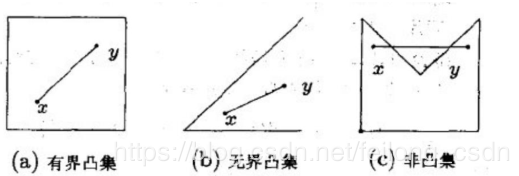
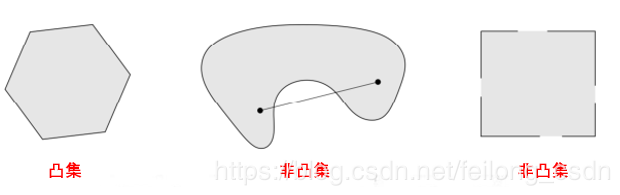
凸函数定义

$f(x)$为凸集$S$在上的函数，任意$x_1,x_2$$\in S$,任意$\lambda \in (0,1)$ 若$$f(\lambda x_1+(1-\lambda )x_2)\le \lambda f(x_1)+(1-\lambda )f(x_2)$$ 恒成立，则$f(x)$为凸集$S$上的凸函数。当等号去掉时，是严格意思上的凸函数。
注： 线性函数既是凸函数也是凹函数。

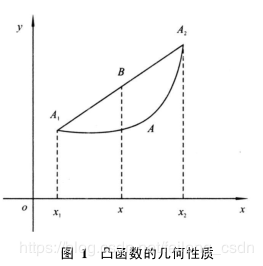
凸函数判断

$f(x)$在凸集$S$上连续二阶可微，则$f(x)$为凸函数的充分必要条件为，二阶导$f^{\prime \prime }(x)>0$，对于多元函数，则Hassion矩阵为半正定矩阵。

凸函数的性质

琴生不等式

$$f(\sum _{i=1}^n{w}_i{x}_i)<=\sum _{i=1}^n{w}_{i}f(x_i)$$
$i=2$时，由定义知是满足条件的，可由数学归纳法进行证明。

凸优化问题的局部最小是全局最小值

机器学习中将问题转化成凸优化问题后，便可以求解全局最小，这也是都希望所研究的问题是凸优化问题的原因。由图形可知，不会存在局部平衡点，存在则不是凸函数。

凸函数相加还是凸函数

$f(x)，g(x)$都是凸集$S$上的凸函数，则$y(x)=f(x)+g(x)$也是凸函数。

Jessen不等式

$f(x)$为凸集$S$上的凸函数，$E(x)$为$x$的期望，则
$$f(E(x))\le E(f(x))$$

参考博客

• https://blog.youkuaiyun.com/feilong_csdn/article/details/83476277 作者：feilong_csdn
• https://blog.youkuaiyun.com/u014170677/article/details/21873981 作者：滴水札记