Codeforces Round 1030 (Div. 2) D2 ~ E题解

D2. Red Light, Green Light (Hard version)

对于每个位置是否能在 $10^{100}$ 秒内离开，实际上等价于问你从该位置开始走是否会陷入死循环。

当我们经过每一个红绿灯灯，要么是朝向是往左的，记为 $L$，要么朝向是往右的，记为 $R$。

不妨假设我们当前所在的位置是第 $i$ 个红绿灯处，即位置为 $p_i$，且方向为 $R$，该灯此时为红色。

设往右走到第 $j$ 个红灯处需要折返，其位置为 $p_j$，则需要满足
$$p_j-p_i+d_i\equiv d_j(\mathrm{mod}k)\text{\hspace{1em}(1)}$$
设往左走到第 $j$ 个红灯处需要折返，其位置为 $p_j$，则需要满足
$$p_i-p_j+d_i\equiv d_j(\mathrm{mod}k)\text{\hspace{1em}(2)}$$
而对于一个红灯 $i$ 而言，从 $i$ 出发往左边或右边走，至多碰到一个红灯。

不妨预处理出每个红灯往左或右走遇到的第一个红灯，那么整个路线图就是一个有向图。

如果无法走出去，说明我们从图上的一点出发一定会走到一个环内。

向右走

考虑如何建图，对于一个红绿灯 $i$，可以设 $i$ 表示往右走，$i+n$ 表示往左走。

$$d_i-p_i\equiv d_j-p_j(\mathrm{mod}k)\text{\hspace{1em}(1’)}$$
所以对于每个红绿灯 $i$，我们只要从后往前找离 $i$ 最近的满足式子 $(1^{\prime })$ 的红绿灯即可。

即 $i\to j+n$ 连边，因为我们已经规定所有 $i<n$ 都表示往右边走，所有 $j>n$ 都表示往左边走。

所以我们对于每个红绿灯 $i$ 要往右边走的话，假设遇到的第一个红灯是 $j$，则必须连接 $j+n$。

vector <int> g[2*n + 2];
map <int, int> R;
for (int i = n; i >= 1; i--) {
   int res = ((d[i] - p[i]) % k + k) % k;
   if (R.count(res)) g[i].emplace_back(R[res]);
   R[res] = i + n;
}

向左走

对于每一个红绿灯 $i+n$，我们只需要从前往后找离 $i$ 最近的满足式子 $(2^{\prime })$ 的红绿灯即可。
$$d_i+p_i\equiv d_j+p_j(\mathrm{mod}k)\text{\hspace{1em}(2’)}$$

map <int, int> L;
for (int i = 1; i <= n; i++) {
   int res = (d[i] + p[i]) % k;
   if (L.count(res)) g[i + n].emplace_back(L[res]);
   L[res] = i;
}

判断环

接下来考虑如何判断每个点是否一定到达环？

根据上面的分析，一个红绿灯朝一个方向至多只有一条出边。

考虑直接从入度为 0 的点开始 DFS，对于图中的每一个点维护两个标记，第一个是否被访问过，第二个是是否会到达环。

对于当前的一次 DFS，如果发现从 $u$ 出发有一条边到达 $v$ 且 $v$ 是被访问过的点，说明这整个连通块都能到达环。

因为从入度为 $0$ 的点开始，最终如果存在点没被访问过，说明这个点必然存在环里。

// 是否被访问过，是否能到达环
vector <int> vis (2*n + 1, 0), circle(2*n + 1, 0);
function <void(int)> dfs =[&] (int u) {
   vis[u] = 1;
   for (auto v : g[u]) {
       if (!vis[v]) {
           dfs(v);
       }else {
           circle[u] = 1;
       }
       if (circle[v] == 1) circle[u] = 1;
   }
};

// 更新入度
vector <int> indgree(2*n + 1, 0);
for (int i = 1; i <= 2*n; i++) {
   for (auto v : g[i]) {
        indgree[v] ++;
   }
}

// 找到所有入度为0的点进行搜索
for (int i = 1; i <= 2*n; i++) {
   if (!indgree[i] && !vis[i]) {
       dfs (i);
   }
}

// 如果没被搜索过，说明在循环内
for (int i = 1; i <= 2*n; i++) {
   if (vis[i] == 0 && indgree[i]) circle[i] = 1;
}

因为题目会给出若干个起点，且规定方向是朝右，我们需要判断这个起点是否会陷入循环。

找到这个起点往右走能到达的第一个红灯即可。

假设其第一个到达的红灯是 $i$，则有
$$p_i-x\equiv d_i(\mathrm{mod}k)$$
等价于
$$p_i-d_i\equiv x(\mathrm{mod}k)$$

可以对每个 $(p_i-d_i)(\mathrm{mod}k)$ 按余数分类，然后每个类里存放红绿灯的位置序列，二分查找第一个大于等于 $x$ 的位置的红灯即可。

不妨设这个红灯是 $i$，则只需要判断 $circle[i+n]$ 是否为 $1$ 即可。

#include <bits/stdc++.h>
using namespace std;
#pragma GCC optimize(2)
#define ll long long
#define PII pair<int,int>
#define endl "\n"
#define INF 1e18
#define int long long
const int N = 1000005; // 1e6 + 5

void solve () {
    int n, k;
    cin >> n >> k;

    vector <int> p(n + 1), d(n + 1);
    for (int i = 1; i <= n; i++) cin >> p[i];
    for (int i = 1; i <= n; i++) cin >> d[i];

    vector <int> g[2*n + 2];

    //往右边建边
    map <int, int> R;
    for (int i = n; i >= 1; i--) {
        int res = ((d[i] - p[i]) % k + k) % k;
        if (R.count(res)) g[i].emplace_back(R[res]);
        R[res] = i + n;
    }

    //往左边建边
    map <int, int> L;
    for (int i = 1; i <= n; i++) {
        int res = (d[i] + p[i]) % k;
        if (L.count(res)) g[i + n].emplace_back(L[res]);
        L[res] = i;
    }



    // 是否被访问过，是否能到达环
    vector <int> vis (2*n + 1, 0), circle(2*n + 1, 0);
    function <void(int)> dfs =[&] (int u) {
        vis[u] = 1;
        for (auto v : g[u]) {
            if (!vis[v]) {
                dfs(v);
            }else {
                circle[u] = 1;
            }
            if (circle[v] == 1) circle[u] = 1;
        }
    };

    // 更新入度
    vector <int> indgree(2*n + 1, 0);
    for (int i = 1; i <= 2*n; i++) {
        for (auto v : g[i]) {
             indgree[v] ++;
        }
    }

    // 找到所有入度为0的点进行搜索
    for (int i = 1; i <= 2*n; i++) {
        if (!indgree[i] && !vis[i]) {
            dfs (i);
        }
    }

    // 如果没被搜索过，说明在循环内
    for (int i = 1; i <= 2*n; i++) {
        if (vis[i] == 0 && indgree[i]) circle[i] = 1;
    }

    map <int, int> pos1;
    for (int i = 1; i <= n; i++) pos1[p[i]] = i;

    map <int, vector<int>> pos2;
    for (int i = 1; i <= n; i++) {
        pos2[((p[i] - d[i]) % k + k) % k].emplace_back(p[i]);
    }

    int q;
    cin >> q;
    while (q--) {
        int x;
        cin >> x;
        if (!pos2.count(x%k)) cout << "YES" << endl;
        else {
            auto pos = lower_bound(pos2[x % k].begin(), pos2[x % k].end(), x);

            if (pos == pos2[x % k].end()) cout << "YES" << endl;
            else {
                cout << (circle[pos1[*pos] + n] == 1 ? "NO" : "YES") << endl;
            }
        }
    }
}

signed main () {
    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    int t;
    cin >> t;

    while(t--){
        solve();
    }
}

E. Grid Coloring

受到惩罚的条件是

1. 受惩罚的格子距离当前被涂色的格子的水平距离或竖直距离最远。
2. 满足 $1$ 的所有格子中距离当前涂色的格子的曼哈顿距离最大。

根据条件 $1$ 可知，如果矩阵四条边上都有格子被染色，那么矩阵中任意一个格子被染色，都只会导致四条边中的某几条边上的格子受到惩罚。

因为我们一定能找到一个最小矩形将当前被涂色的格子全部圈起来。

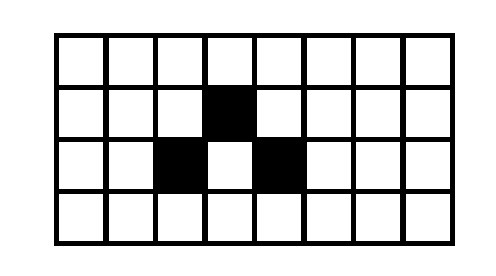
最小的矩形是绿色方框所示的 $2\times 3$ 矩形。

如果我们给最小矩形内的格子染色，那么受到惩罚的必然是这个最小矩形的某些边界上的格子，且最小矩形的非边界部分一定不会受到惩罚。

于是有一个非常自然的思路，就是先给一个小方格涂色，此时最小矩形是 $1\times 1$ 大小，若最小矩形内所有方格涂满了颜色，则往最小矩形外的相邻一个染色使得最小矩形被逐渐扩大，然后再重复这样的过程，直到最小矩形扩大到 $n\times m$。

但是也有问题，就是我们往最小矩形外拓展的次序需要是合理的。

如当前最小矩形内部全部被涂色

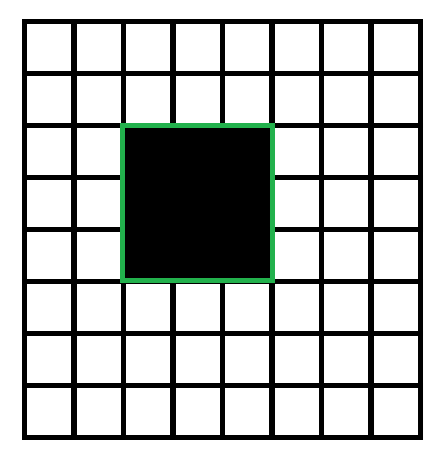
我们现在往外拓展一个格子，此时最小矩形变成

如果我们给剩下的两个矩形填色的话，绿色矩形的右下角会新增惩罚值会增加 $2$，这个惩罚值增加过多了。

我们可以采取这样的扩展策略，当最小矩阵内部满了，那么采取关于中心对称的策略进行染色。

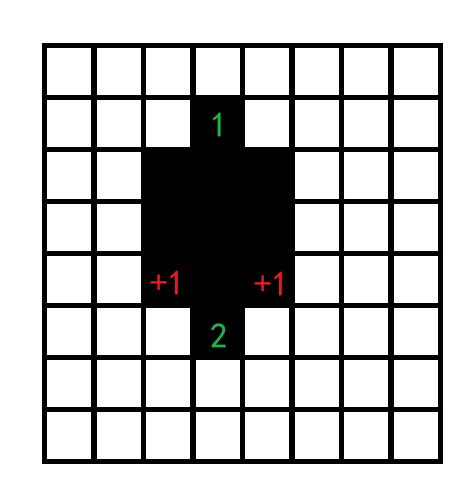
对于这幅图，我们对称地染色，先把中心点正上方的格子染色，图中红色的表示惩罚值 $+1$，绿 $1$ 会给原矩阵内部的格子加上 $1$ 个惩罚值。

然后再染对称点，也就是用绿 $2$ 标识的格子，此时受罚点是与绿 $1$ ，其惩罚值为 $1$，然后染色可以按照下图顺序进行

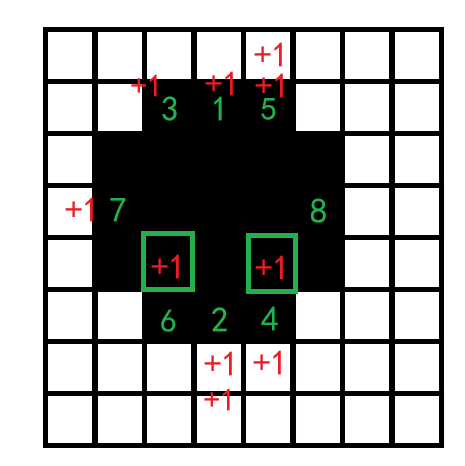
接下来给绿 $3$ 染色表示它是第三个被染色的，然后绿 $2$ 的惩罚值加 $1$。

接下来给绿 $4$ 染色表示它是第四个被染色的，然后绿 $3$ 的惩罚值加 $1$。

以此类推，当中心点的上下被染色完了之后去染色左右的边界上的点。

还是每两次染色为一组，染关于中心点对称的点。

最后还剩下四个角，可以分成两组染色，每组两个点，每个点关于中心点对称。

此时我们如果作出染色图，我们会发现边角中的点的惩罚值至多为 $1$。这便于我们下一次扩展。

采用这样的染色方法，只能染出一个正方形，其边长至多为 min⁡{n,m}\min\{n,m\}min{n,m}。

若 $n>m$，说明竖直方向还没染完，依旧采用刚刚的策略，把正方形往上下扩展。

若 $n<m$，说明水平方向还没染完，依旧采用刚刚的策略，把正方形往左右扩展。

#include <bits/stdc++.h>
using namespace std;
#pragma GCC optimize(2)
#define ll long long
#define PII pair<int,int>
#define endl "\n"
#define INF 1e18
#define int long long
const int N = 1000005; // 1e6 + 5

void solve () {
    int n, m;
    cin >> n >> m;

    int min_len = min(n, m);
    int mid_x = (n + 1)/2, mid_y = (m + 1)/2;
    cout << mid_x << ' ' << mid_y << endl;

    for (int i = 1; i <= min_len/2; i++) {
        int len = i * 2 + 1;
        // 处理上下
        cout << mid_x - i << ' ' << mid_y << endl;
        cout << mid_x + i << ' ' << mid_y << endl;

        for (int j = 1; j <= len/2 - 1; j++) {
            // 左上一个，右下一个
            cout << mid_x - i << ' ' << mid_y - j << endl;
            cout << mid_x + i << ' ' << mid_y + j << endl;

            // 右上一个，左下一个
            cout << mid_x - i << ' ' << mid_y + j << endl;
            cout << mid_x + i << ' ' << mid_y - j << endl;
        }

        // 处理左右
        cout << mid_x << ' ' << mid_y - i << endl;
        cout << mid_x << ' ' << mid_y + i << endl;

        for (int j = 1; j <= len/2 - 1; j++) {
            // 左上一个，右下一个
            cout << mid_x - j << ' ' << mid_y - i << endl;
            cout << mid_x + j << ' ' << mid_y + i << endl;

            // 左下一个，右上一个
            cout << mid_x + j << ' ' << mid_y - i << endl;
            cout << mid_x - j << ' ' << mid_y + i << endl;
        }

        // 处理四个对角
        cout << mid_x - i << ' ' << mid_y - i << endl;
        cout << mid_x + i << ' ' << mid_y + i << endl;
        cout << mid_x + i << ' ' << mid_y - i << endl;
        cout << mid_x - i << ' ' << mid_y + i << endl;
    }

    if (n > m) {
        // 往上下两边扩展。
        for (int i = 1; i <= (n - min_len)/2; i++) {
            int len = m;
            // 处理上下
            cout << mid_x - min_len/2 - i << ' ' << mid_y << endl;
            cout << mid_x + min_len/2 + i << ' ' << mid_y << endl;

            for (int j = 1; j <= len/2; j++) {
                // 左上一个，右下一个
                cout << mid_x - min_len/2 - i << ' ' << mid_y - j << endl;
                cout << mid_x + min_len/2 + i << ' ' << mid_y + j << endl;

                // 右上一个，左下一个
                cout << mid_x - min_len/2 - i << ' ' << mid_y + j << endl;
                cout << mid_x + min_len/2 + i << ' ' << mid_y - j << endl;
            }
        }

    } else if (m > n) {
        // 往上下两边扩展。
        for (int i = 1; i <= (m - min_len)/2; i++) {
            int len = n;
            // 处理上下
            cout << mid_x << ' ' << mid_y - min_len/2 - i << endl;
            cout << mid_x << ' ' << mid_y + min_len/2 + i << endl;

            for (int j = 1; j <= len/2; j++) {
                // 左上一个，右下一个
                cout << mid_x - j << ' ' << mid_y - min_len/2 - i  << endl;
                cout << mid_x + j << ' ' << mid_y + min_len/2 + i << endl;

                // 右上一个，左下一个
                cout << mid_x + j << ' ' << mid_y - min_len/2 - i << endl;
                cout << mid_x - j << ' ' << mid_y + min_len/2 + i << endl;
            }
        }
    }
}

signed main () {
    std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);

    int t;
    cin >> t;

    while(t--){
        solve();
    }
}