程序员的数学之归纳法

据说德国数学家约翰·卡尔·弗里德里希·高斯在9岁时遇到一个问题：如何计算出`1 + 2 + 3 + ...... + 99 + 100`的值。

要是对数学不熟悉或者没有学过数列相关知识的话，可能会一个个相加。

`100`、`200`，甚至`300`以内还能勉强这样做，但如果要从`1`加到`1亿`，就不可能继续用这种土办法了。

人家到底是个天才，他没有像普通人一样一个个加，而是这么想的。

• `1 + 2 + 3 + ...... + 99 + 100`和`100 + 99 + 98 + ...... + 2 + 1`值肯定是相等的。
• 把它们相加除以2就可以了。

所以，一个求数列的问题就变成了计算`面积`的问题。为什么是`面积`？

因为单个`1 + 2 + 3 + ...... + 99 + 100`可以用数字阶梯来表示，就像下面这样。

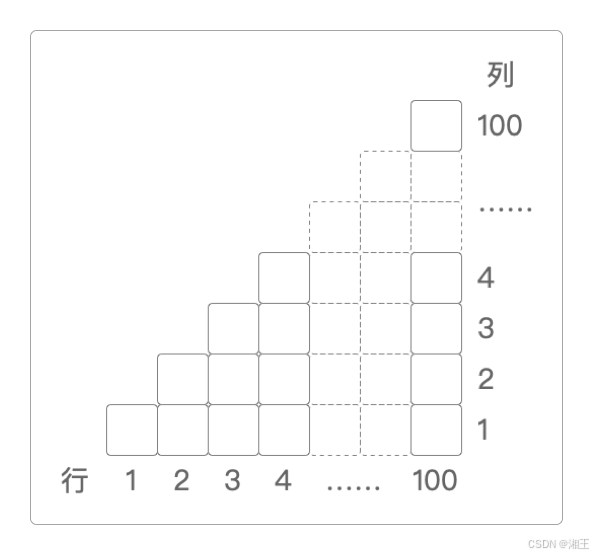
而两个数字阶梯，就可以`组合`成一个`长方形`。

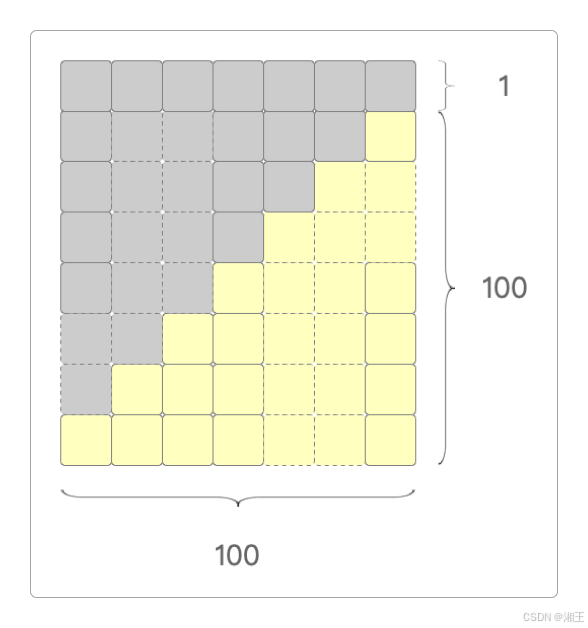
求`1 + 2 + 3 + ...... + 99 + 100`的值，就变成了计算黄色部分方块的面积了，真是太巧妙了。

所以它的公式用肉眼就能看出来：`(1 + 100) × 100 / 2`。

这就是数列计算公式`(1 + n) × n / 2`的由来——现在终于知道为什么要除以`2`了，因为就是只计算一半的面积。